Received 21 December 2015; accepted 6 April 2016; published 13 April 2016

ABSTRACT

Hyperspectral unmixing is a powerful tool for the remote sensing image mining. Nonnegative matrix factorization (NMF) has been adopted to deal with this issue, while the precision of unmixing is closely related with the local minimizers of NMF. We present two novel initialization strategies that is based on CUR decomposition, which is physically meaningful. In the experimental test, NMF with the new initialization method is used to unmix the urban scene which was captured by airborne visible/infrared imaging spectrometer (AVIRIS) in 1997, numerical results show that the initialization methods work well.

Keywords:

Nonnegative Matrix Factorization, Hyperspectral Image, Hyperspectral Unmixing, Initialization Method

1. Introduction

Given a non-negative matrix 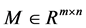and a desired rank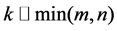, the non-negative matrix factorization aims to find two matrices 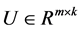and with the non-negative elements such that

(1)

Problem (1) is commonly reformulated as the following minimization problem:

(2)

Due to non-subtractive combinations of non-negative basis vector, NMF can give a simple interpretation in many areas. We are concerned with its application of analyzing data obtained using astronomical spectrometers, which provide nonnegative spectral data [1]. Determining what smaller sub-elements make up a pixel is called unmixing. The observed spectra represents a linear mixture of spectra underlying consistent compounds and the aim of NMF is to extract the desired spectra and provide the information on their abundance. Each row vector of the original matrix M represents an observed mixed spectrum at certain wavelength, while each column of M give the spectral signature of a given pixel. In such way, each element 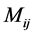of M is equal to the reflectance spectra of the jth pixel at the ith wavelength. With the help of NMF, M is approximated by the product of U and V. In hyperspectral unmixing, U is often thought of as the endmember or source matrix, which give the spectral signature of 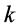different materials on the ground and V is the fractional abundance matrix.

Many algorithms have been designed for solving (2). Most of these algorithms can be classified into two categories: gradient descent methods [2] [3] and alternating non-negative least squares [4]. There are two main difficulties when applying NMF in hyperspectral image analysis. One is the time consuming of the optimization based algorithms, the other is the nonunique of the NMF solutions.

Since NMF is a nonconvex optimization problem, the iterative methods typically converge slowly to a local minima. It’s said that a good initialization can improve the speed and the accuracy of the solutions of many NMF algorithms as it can produce faster convergence to an improved local minima [5].

Originally, the factor matrices are initialized with random numbers between 0 and 1. The random initialized matrices are dense and do not provide a good estimate for U and V. In order to obtain better solutions, some researchers have tried to improve the initialization phase. Wild [6] proposed the centroid initialization which based on spherical k-means. Unfortunately, it is expensive as a preparing step for NMF. Boutsidis [7] designs nonnegative double singular value decomposition (NNDSVD) to enhance the initialization stage of NMF, which can be combined with all the existing NMF algorithms. But the factor matrices given by NNDSVD is deterministic. Once the obtained solution is unsatisfactory, we could not get a better local minima with the multiple runs of NNDSVD. Later, Langvill et al. give the random Acol, random C initialization and the co-occurence initialization. The random Acol get the factor matrix U by select k random columns of M. Rand C initialization is inspired by the C matrix of CUR decomposition, which is similar with random Acol, with another restriction that the k random columns of W should be the k longest columns of W. Finally, co-occurence initialization is based on the co-occurence matrix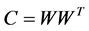, this procedure is expensive.

CUR decompositions approximate the data matrix M by using a small number of actual columns of M. In hyperspectral image analysis, these methods find endmembers that are already present in the data. By doing this, these methods are easily interpretable. However, the endmembers should by contained within the data. It is called the pixel purity assumption, which is a strong requisite. Applying the column selection technique of CUR in the initialization stage of NMF is called Acol. In this paper, we give two new initialization methods for NMF which is based on CUR.

2. CUR Based Initialization

Let be a subset of t columns from M. This subset will make up the candidate columns, which we’ll have to choose from. It should be noted that, this will help to maintain the sparsity in M, which would be lost with pure random initialization with dense vectors or SVD initialization.

2.1. Initialization with SAD

The spectral angle distance (SAD) describes the difference between the true endmembers and the estimated endmembers. It is defined as follows,

(3)

where 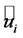is the ith true endmember, and is the ith estimated endmember. The value of SAD range from 0 to represents the similarity of 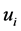and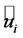. When comes close to 0, the estimated endmember matches the true endmember well.

is randomly selected form M, then is initialized by finding a submatrix of. Each column of is constrained to have the smallest SAD with the true endmember.

2.2. Initialization with SKLD

Given a random vector, the probability vector p associated with u is

(4)

Then, the entropy of w is given by

(5)

We employ the symmetrized Kullback Leibler (KL) divergence to select the columns from. Let denoted the KL divergence of d from w,

(6)

where. In our paper, w is a column selected form, while d is the true endmember.

KL divergence is a measure of information lost, when d is used to approximated w. Since the KL divergence is not symmetric and does not satisfy the triangle inequality, the following symmetrized KL divergence is considered.

(7)

Once a column from has the smallest with the true endmember, it is selected as one column of the initialized matrix.

3. Numerical Experiments

In this section, we compare our initialization strategy with the Urban hyperspectral image, which is taken from HYper-spectral Digital Imagery Collection Experiment (HYDICE) air-borne sensors. It contains 162 clean

bands and pixels for each spectral image. The original matrix we obtained from this image is.

We will first look at the performance of four initialization techniques: random, rand columns (Acol), random selected columns from M with SAD (SADcol) and random selected columns with SKLD (SKLDcol). It is said that the active set type NMF method is a good choice to solve the spectroscopy data, so we combine the above four initialization with the active set method proposed in [8]. For each run of the NMF algorithm, we use the

Frobenius norm of the error, be our performance criterion. In order to avoid the influence of the randomness, each initialization method run 10 times and the average Frobenius error is computed.

Since the random initialization has nothing to do with the measured spectra signal, the Frobenius error in the beginning is bigger than the other methods. It can be seen from Figure 1 that SADcol gives the lowest Frobenius error. The Frobenius error becomes smaller and smaller as the iteration going on. We also compare the running time of these four initialization methods.

Table 1 show that SADcol is faster than the other schemes. Both SADcol and SKLDcol give the good initialization, they improve the speed of NMF efficiently.

4. Conclusion

Two initialization methods for NMF are proposed in this paper. With the help of the SAD and SKLD measure, the Frobenius error is lower than the rand and Acol. Since is selected from the original matrix, it maintains sparsity and physical interpretation. Numerical results show the efficient of the two initialization methods.

Acknowledgements

The work was supported in part by the National Science Foundation ofChina (41271235, 10901094,11301307), The national science and technology support program(2013BAD05B06-5). The Excellent Young Scientist Foundation ofShandong Province (BS2011SF024, BS2012SF025) and Young TeacherFoundation of Shandong Agricultural University (23744).

Cite this paper

Li Sun,Gengxin Zhao,Xinpeng Du, (2016) CUR Based Initialization Strategy for Non-Negative Matrix Factorization in Application to Hyperspectral Unmixing. Journal of Applied Mathematics and Physics,04,614-617. doi: 10.4236/jamp.2016.44068

References

NOTES

^*Corresponding author.