Journal of Geographic Information System, 2011, 3, 195-210
doi:10.4236/jgis.2011.33016 Published Online July 2011 (http://www.SciRP.org/journal/jgis)
A Spatially Heterogeneous Expert Based (SHEB) Urban
Growth Model Using Model Regionalization
Dimitrios Triantakonstantis, Giorgos Mountrakis, Jida Wang
Department of Environmental Resources Engineering, State University of New York College of Environmental Science
and Forestry , Syracuse, USA
Received March 26, 20 1 1; revised May 13, 2011; accepted Ma y 25, 2011
Abstract
Urbanization changes have been widely examined and numerous urban growth models have been proposed.
We introduce an alternative urban growth model specifically designed to incorporate spatial heterogeneity in
urban growth models. Instead of applying a single method to the entire study area, we segment the study area
into different regions and apply targeted algorithms in each subregion. The working hypothesis is that the
integration of appropriately selected region-specific models will outperform a globally applied model as it
will incorporate further spatial heterogeneity. We examine urban land use changes in Denver, Colorado. Two
land use maps from different time snapshots (1977 and 1997) are used to detect the urban land use changes,
and 23 explanatory factors are produced to model urbanization. The proposed Spatially Heterogeneous Ex-
pert Based (SHEB) model tested decision trees as the underlying modeling algorithm, applying them in dif-
ferent subregions. In this paper the segmentation tested is the division of the entire area into interior and ex-
terior urban areas. Interior urban areas are those situated within dense urbanized structures, while exterior
urban areas are outside of these structures. Obtained results on this model regionalization technique indicate
that targeted local models produce improved results in terms of Kappa, accuracy percentage and multi-scale
performance. The model superiority is also confirmed by model pairwise comparisons using t-tests. The
segmentation criterion of interior/exterior selection may not only capture specific characteristics on spatial
and morphological properties, but also socioeconomic factors which may implicitly be present in these spa-
tial representations. The usage of interior and exterior subregions in the present study acts as a proof of con-
cept. Other spatial heterogeneity indicators, for example landscape, socioeconomic and political boundaries
could act as the basis for improved local segmentations.
Keywords: Urban Growth Models, Spatial Heterogeneity, Model Fusion, Decision Trees, Denver
1. Introduction
Urbanization is a phenomenon observed since ancient
times. It has been strengthened and acquired global mag-
nitude over the last two centuries. More specifically, in
year 1800 only 2% of p eople lived in cities, while in year
1900 the ratio incr eased to 12%. In year 2008, more th an
50% of the world population lived in urban areas [1], and
it is estimated that by year 2025 80% of human popula-
tion will live in cities [2]. This transition has and will
change further socioeconomic structure, environmental
resource allocation and ecosystem behavior. Urban en-
vironmental planning has been quantitatively and quali-
tatively supported by applying weighted overlay methods
to the driving factors [3], as well as geostatistical tech-
niques as an important part of the GIS-SPRING software
capabilities [4]. It is therefore crucial to develop models
for urban growth prediction to support interdisciplinary
policy decisions for a sustainable future.
Numerous models have been recently developed for
land use change prediction (for example [5-9]). The in-
fluence of biophysical and socioeconomic factors on land
use changes has been an important issue in scientific
debates [10] and significant investments are made in the
understanding of linkages between ecosystems, climate
and land use. For example, the National Science Founda-
tion currently invests $22.5 million to human-environ-
ment research, with a significant portion devoted to land

D. TRIANTAKONSTANTIS ET AL. 196
use models [11].
Typically, land use models examine the likelihood for
an area to be transformed from one land type to another
[12]. Using available biophysical and socioeconomic
variables as driving fo rces, approaches like linear/logistic
regression, and heuristic methods of multicriteria evalua-
tion can be adopted [13-15]. Logistic regression is a spe-
cial case of generalized linear model, which is used to
predict probabilities for the presence or the absence of a
specific geographic characteristic. It has been widely
used in urbanization [16-18]. In [19] logistic regression
was used in order to predict urban-rural land conversion
in a multi-temporal environment. Moreover, autologistic
regression models have been developed in order to han-
dle spatial autocorrelation. An additional explanatory
variable, named autocovariate term can be applied to the
logistic regression equation to correct the effect of spatial
autocorrelation in a given neighborhood [20-22]. An
alternative to the inclusion of spatial autocorrelation in
the model expression is the introduction of an optimal
sampling scheme to eliminate the spatial autocorrelation
within the distance it occurs [19,23].
Other models use fuzzy set theory as a method for
dealing with imprecision of the data and determination of
class boundaries [24-26]. Algorithms such as support
vector machines [27-29] have been successfully applied
to land use chan ge modeling. Neighborhoo d effects are a
major factor of land use dynamics [17,30-34] and an
important component in many land use change models.
The most common method to implement neighborhood
interactions in land use change models is cellular auto-
mata [35 ,36], wh ere th e transition of a cell from one land
use to another depends on the land use of its neighboring
cells [37-40].
Artificial Neural Networks (ANNs) model complex
relationships between variables, playing an important
role as a non parametric approach in land use modeling
[41-43] and land use change modeling [44-46]. In [47] a
Land Transformation Model was successfully developed
where social, political and environmental factors were
examined to predict urbanization. This model was further
used to forecast land use from 2000 to 2020 and the as-
sessment was achieved using alternative drivers of land
use such as forest species [48]. Another approach for
future prediction of urban growth has been presented in
[49], where the ART-MMAP, a neural network model,
produces a prediction map under different scenarios re-
lated to historical urban growth data, land use drivers and
socioeconomic data. ANNs have been also used for cali-
bration and simulation of cellular automata models in
urban systems [50,51]. ANN-based cellular automata
models were also proposed for categorizing the cell tran-
sition in a binary way (urban/non urban) [52,53]. More-
over, in [54] a generalized approach was introduced for
multiple urban uses simulations (e.g. residential, com-
mercial, and industrial).
Decision tree is another non-parametric learning algo-
rithm widely used in land use/land cover modeling
[55-59]. Structurally, it differentiates discrete instances,
e.g. urban land use categories, through sequentially sort-
ing down a bottom-up tree from the root/upper to the
leaf/lower nodes. Each node represents a targeted attrib-
ute whose value is determined by a partitioning rule as-
sociated to the branch descending from the upper-level
node [60]. Compared to generalized linear models, a
decision tree is more robust to data distribution such as
outliers or missing values, and more flexible in estab-
lishing rules that are spatially heterogeneous [61]. Com-
pared to other non-parametric approaches such as ANNs,
rules established by decision trees are structurally simple
and readily interpretable [55]. However, traditional deci-
sion trees treat data as a collection of independent ob-
servations, and thus exclude the influence of data spatial
autocorrelation in the training process. This limitation
has been investigated by a spatial entry-based decision
tree designed by [56] where a notion of “spatial entropy”
was proposed.
An important aspect of urbanization is spatial hetero-
geneity [62]. It was soon realized that similar values in
an explanatory variable may have different effects in the
urban development of different areas and therefore must
be treated separately. Although a decision tree univer-
sally incorporates a higher degree of spatial heterogene-
ity, the robustness is yet limited by its intrinsic sin-
gle-algorithm structure where the complete area is indis-
criminately targeted into a global rule [63,64]. Classifi-
cation and regression trees were used to divide a forested
area into homogeneous parts in order to localize the
global model [65].
The urban spatial structure and change dynamics can
be better described by applying spatial metrics
[58,66-68]. Spatial metrics de scribe spatial heterogeneity
by dividing large areas into homogenous subregions.
Examples of metrics used to quantify the spatial hetero-
geneity include patch size, patch density, edge length,
distance from nearest neighbor and contagion among
others [69]. Moreover, the fractal dimension is also im-
plemented as a spatial metric to describe patch complex-
ity [70,71]. In [72] a region-based system was developed
to deal with the spatial and morphologic characteristics
of urban structures. Spatial heterogeneity also exhibits
scale dependency [73,74]. In [75] a clustering approach
was used to map urban influence at multiple scales; the
micro, meso and macro scales have been a useful foun-
dation for exploring spatial dynamics of urban structure,
addressing spatial, temporal and behavioral complexity

D. TRIANTAKONSTANTIS ET AL. 197
[11].
This paper investigates whether integration of spatially
unique models improves on capturing spatial heterogene-
ity. We investigate whether an expert-based selection of
multiple models operating in different spatial regions
outperforms a global model with the same input vari-
ables (including the segmentation variables) using an
identical training dataset. Our implementation includes
decision tree classifier and variable training data sizes on
a binary urbani zat i on prediction task .
2. Study Area and Modeling Data
2.1. Study Area
The study area is located in the Denver metropo litan area,
Colorado, which is in the center of the Front Range Ur-
ban Corridor, with the Rocky Mountains from the west
and the High Plains from the east. The area selected for
this study covers the major part of Denver metropolitan
area and is specified by Xmin : 481862m, Xmax: 522032m
and Ymin: 4389809m and Ymax: 4421313m (UTM Zone
13 North), as Figure 1 shows. Denver has experienced a
large urban growth from 1977 to 1997. According to
land use maps, provided by the U.S. Geological Survey
Rocky Mountain Mapping Centre
(http://rockyweb.cr.usgs.gov/frontrange/datasets.htm),
the percentage of urban growth from 1977 to 1997 was
20.8% (urban areas in 1977: 48% and 1997: 58% of the
total study area). This rapid urban growth was the moti-
vation behind this site selection for our model develop-
ment.
2.2. Response and Predictor Variables
The urban development is the response variable in this
current study. The non-developed areas in 1977 that are
converted to developed areas in 1997 are assigned as 1
into the response variab le, while the non -developed ar eas
1977 which remain the same in 1997 are given the 0
value. The developed areas in 1977 are excluded from
the model and we also assume no conversion from de-
veloped back to non-developed area. The urban devel-
oped areas include residential areas, commercial/light
industries, institutions, communication and utilities,
heavy industries, entertainments/recreations, roads and
Figure 1. Urbanization changes in the Denver, CO metropolitan area.

D. TRIANTAKONSTANTIS ET AL. 198
other transportation.
We examine 21 predictor variables which are pro-
duced using Euclidean distances to the nearest neighbor
and Kernel density filters. The predictor variables in-
clude: a) Euclidean distance to entertainment venues,
heavy industries, rivers, primary roads, secondary roads
and minor roads, b) Kernel density (radius: 120 pixel) of
agricultural business, residential areas, urban develop-
ments, commercial areas, institutes/schools, communica-
tions/utilities, lands/ponds, cultivated lands and natural
vegetations, c) Kernel density (radius: 10, 30, 50, 80, 100,
150) of distance to urban developments. All the afore-
mentioned variables were based on 1977 vector data, no
information from 1997 was incorporated as that was our
prediction year. Furthermore, elevation and slope are
also considered, making 23 the to tal number of predictor
variables. Statistical analysis in this study area shows
that distance to entertainment, density of residential areas,
density of urban development and density of natural
vegetations contribute with higher importance in model-
ing the urban growth than the other predictor variables
[68]. The final form of the dataset expressing response
and predictor variables is in a raster representation with a
30m spatial resolution.
3. Model Development
3.1. Theoretical Underpinnings
Several algorithms have been proposed for urban mod-
eling with varying complexity and success. A motivating
factor behind algorithmic selection relies on an algo-
rithm’s ability to capture spatial heterogeneity. The cur-
rent approach is to rely solely on algorithmic complexity
to adjust model behavior in different regions of the entire
study site. In this paper we examine whether a segmenta-
tion of the study area in subr egions follow ed by selective
application of methods within each subregion would lead
to improved modeling capabilities. In other words
through model regionalization we challenge the current
expectation that a highly complex globally applied
method can sufficiently recognize local heterogeneity
and fine tune performance accordingly.
From the model development perspective, we train
different models in different subregions and then spa-
tially group the results obtained. These subregions are
identified based on expert knowledge on different ur-
banization drivers. In order to allow a global model to
directly compete with our numerous local models the
segmentation criterion used to define subregions is also
incorporated as an additional input variable to the global
model. Therefore the global model has equal opportunity
to capture heterogeneity as the local models, because the
same input variables and the same modeling techniques
are implemented in both cases.
We apply decisions trees in order to evaluate our hy-
pothesis of multiple local models outperforming a global
one. Decision trees are a popular modeling technique as
in addition to advanced modeling capabilities, they still
remain easy to understand as they can be converted to a
set of rules. Decision trees use a training dataset in order
to construct the model structure and the produced model
is applied to a different dataset (validation) to estimate
the prediction accuracy. Of particular interest is per-
formance assessment of local vs. global models on a
varying training dataset size. Small training sizes are
cost-efficient to acquire but there is an overfitting cost
associated with them, therefore the identification of
proper balance is investigated.
3.2. Subregion Identification Based on
Heterogeneous Behavior
Extraction of homogenous areas is typically based on
fragmentation analysis where spatial and landscape met-
rics are adopted. A wide range of relevant metrics has
been proposed, especially in ecological applications [67].
In our case fragmentation analysis involved evaluation of
spatial distribution of urban development in the entire
study area. It was found that some areas have higher
propensity for urban development than others; a conse-
quence of urbanization density. More specifically, an
area surrounded by urban structures may experience dif-
ferent development pressures than not surrounded areas
[68].
In our study, the entire area is divided into two subre-
gions: the interior urban subregion, a dense urbanized
area and the exterior urban subregion with no dense ur-
ban structures (Figure 2). These two areas exhibit dif-
ferent propensity for urban development.
Figure 3 demonstrates the cumulative probability that
an undeveloped pixel in 1977 would be developed in
1997 at a given distance. That relationship is clearly dif-
ferent for the interior and exterior subregions at various
distances from already developed areas, which were
measured using Euclidean distances between pixel cen-
ters. Note that the intention of this graph is to provide a
relative comparison between exterior and interior regions
leading to motivation beh ind the model develop ment; the
graphs purpose is not to directly incorporate these prob-
abilities in model design. Undeveloped areas in close
proximity to existing urban structures are more likely to
be converted to urban land use in general, but note that
this probability is significantly higher in interior subre-
gions. This is mainly due to the intense human influen ce
which occurs near existed urban structures in dense ur-
ban environments such as the interior subregion. For
C
opyright © 2011 SciRes. JGIS

D. TRIANTAKONSTANTIS ET AL. 199
Figure 2. Interior and Exterior subregions of the 1977 Undeveloped area.
Euclidean distance from urban areas in 1977 (m)
Figure 3. Development probability as a function of Euclidean proximity to existing urban structures for the interior and exte-
rior subregions.
C
opyright © 2011 SciRes. JGIS

D. TRIANTAKONSTANTIS ET AL. 200
example, the commercial value of these properties may
be higher than places far away from buildings. Therefore,
the decision to separate in the proposed models interior
and exterior areas reflects expert knowledge on expected
urban devel op ment behavior.
Motivated by the divergence in urban development
behavior we develop the proposed local models for each
subregion (one for the interior and another for the exte-
rior) and contrast them with a global model trained and
operating in both subregions simultaneously. Further
segmentations are possible, especially for the exterior
subregion, however this interesting investigation is re-
served for futur e work. The purpo se of this manuscr ipt is
to demonstrate the proof of concept on model regionali-
zation and excite ad ditional research.
3.3. Model Design and Experimental Setup
The proposed Spatially Heterogeneous Expert Based
(SHEB) model uses multiple decision trees to capture
urban growth. The entire study area is divided into the
interior and exterior subregions leading to the creation of
multiple models to test model regionalization benefits. If
a model is trained using samples exclusively from a
subregion it is called Local, if samples come from the
entire study area the name Global is assigned. We also
use a subscript index in the naming structure to reflect
where the model is simulated for validation purposes, for
example Globalint relates to a globally trained model
validated only in the interior subregion. All the Loca l
models are trained and validated exclusively in the same
subregion, therefore the notation Localint for example
suggests a local model trained and validated in the inte-
rior subregion. As a result of the above we have devel-
oped the following models:
 Localint: training and validation dataset from the in te-
rior subregion.
 Localext: training and validation dataset from the exte-
rior subregion.
 Globalint: training dataset from the entire study area,
validation dataset only fro m the interior subregion.
 Globalext: training dataset from the entire study area,
validation dataset only fro m the exterior subregion.
 Globalall: training and validation dataset from the
entire study area.
We should clarify that Globalint, Globalext and
Globalall are the exact same model since they are all
produced from the same training set from the entire study
area; however, model performance is validated in differ-
ent regions to allow comparisons with th e corresponding
Local models.
In order to identify the opti mal balance between Local
and Global models we perform comparisons in each
subregion (interior and exterior) and in the overall site
(all region). The term balance is used to refer to the fact
that not always Local models will outperform global
ones; in every region we compare the corresponding Lo-
cal with the Global model and decide which one to use.
The subregion analysis lead to the following pairwise
comparisons: a) Localint and Globalint, b) Localext and
Globalext. For each subregion, the comparison between
the Local and Global models assesses whether spatial
heterogeneity should be addressed separately in that re-
gion. Depending on the subregion accuracy assessment
the predominant subregion-specific model is selected to
participate further into the SHEB model structure. Since
the SHEB model expects to operate over the entire study
site it is compared against the Globalall model. These
comparisons are presented graphically in Figure 4.
3.4. Algorithmic Specifics
The decision tree models were developed and evaluated
in the Matlab environment. Ten observations were set as
the minimum for a node to be split. Moreover, each deci-
sion tree is adjusted using a 10-fold cross-validation and
a pruning process.
In order to compare Local and Global models we had
to ensure comparable model complexity and input selec-
tion. Regarding input selection the Local models contain
the aforementioned 23 predictor variables (see section
2.2). The Global models incorporate the exact same 23
variables plus an additional predictor variable: a dummy
variable with value of 1 if a point belongs to the interior
subregion and the value of -1 if it lies in the exterior
subregion. By doing so, the Global models have the po-
tential to express the expert-derived interior/exterior
segmentation within their model structure. In terms of
model complexity the decision trees d eveloped for Local
and Global models are directly comparable because the
training of each model took place considering the same
minimum number of points (10 points) classified in
every leaf.
The reference output variable is dichotomous, with
value 1 if the change is from non-urban in 1977 to urban
in 1997, and 0 when the 1977 non-urban areas do not
change. The reference output binary variable is com-
pared with the predicted output of SHEB and Globalall
models. Each set of predictor values is inserted into the
decision tree, which is produced using the regression tree
option in Matlab, and a corresponding response value is
predicted. Because the reference response variable con-
tains only two numeric values, 0 and 1, the correspond-
ing predicted outpu t is a contin uou s variable with a rang e
between 0 and 1, indicating the probability for change.
The closer the probability to 1, the more likely
C
opyright © 2011 SciRes. JGIS

D. TRIANTAKONSTANTIS ET AL. 201
Figure 4. Design scheme of SHEB urban growth model.
this area is to experience urban development. A threshold
is applied in order to categorize the values of the pre-
dicted output into two classes: 0 and 1. In most cases, a
0.5 threshold is used, so as values greater than 0.5 to be
classified to 1 (developed), otherwise to 0 (non-devel-
oped). This value of 0.5 was used as threshold in our
study as well.
3.5. Training Sample Specifics
From the entire study area (710,536 points) we extracted
70% of the data points for validation purposes (497,375
points) and kept the remaining 30% for various training
experiments. The validation dataset contained 389,810
no change and 107,565 change points; spatially it was
distributed to 59,7 55 interior points and 437,620 ex terior
points. All statistics reported in the results section are
calculated using the same validation dataset.
We examined a variety of training sample sizes to as-
sess model performance. We varied the training sample
from 4000 to 30000 with an increment of 4000 leading to
14 different training sets. For a given training sample
total size goal (e.g. 4000 total training points), we ran-
domly selected equal number of interior and exterior
training points (e.g. 2000 for each). Each Local model
was trained with the corresponding points (e.g. the 2000
interior points for the Localint model) and the corre-
sponding Global model used the identical points from
the two Local models combined (e.g. the 2000 interior
points for the Localint model and the 2000 exterior po ints
for the Localext model leading to the 4000 point training
dataset for the Global model). Identical points were used
to support direct comparison between Local and Global
models. Furthermore, for each training dataset total size
(e.g. 4000) we performed 50 random sampling selections
to limit bias especially in smaller size datasets.
Semivariograms analysis showed that spatial autocor-
relation exists within 450m. In order to overcome this
difficulty, training sets were produced using several
random samplings, all at least 450m apart from each
other. Because of the reduced number of training points,
high overfitting occurred with large discrepancies be-
tween calibration and validation accuracies. Therefore,
the spatial autocorrelation is not considered in this paper
and any point could participate in model calibration/
validation.
4. Results
Results from each subregion are presented in the subre-
gion performance assessment section. Using these results
as a guide, a proposed SHEB model is created and con-
trasted with a Global model leading to the entire region
performance assessment. The aggregation statistics in the
entire region put equal weight to both interior and exte-
rior subregions to avoid a site-dependence bias. We
should note that the term prediction relates to the ex-
trapolation on historical data at later times.
4.1. Interior and Exterior Subregion
Performance Assessment
The performance of SHEB model is evaluated using the
confusion matrix and the Kappa statistic. Confusion ma-
trix is produced by cross-tabulation between predicted
and actual variables [76,77]. It is the percentage of pre-
dicted cases which are correctly classified either as urban
or non urban areas. Kappa statistic is a more robust
method in classification accuracy, because it can provide
concordance avoiding the cases which are correctly clas-
sified by chance [78].
In Figure 5 the accuracy results (Kappa, accuracy per-
centage) in the interior and exterior subregions are
graphically displayed by boxplots. Each box contains the
C
opyright © 2011 SciRes. JGIS

D. TRIANTAKONSTANTIS ET AL. 202
median value (central mark) and the 25th and 75th per-
centiles (edges of the box) for 50 random training sets.
The graph presents pairs of local and global models and
they are slightly offset for visualization purposes. Every
pair of local-global is associated with a certain training
sample size that is presented on the X axes. The training
sets of SHEB models for each subregion (inte-
rior/exter ior) vary from 2000 to 15000 points providing a
(a)

D. TRIANTAKONSTANTIS ET AL.203
(b)
Figure 5. Comparison between Local and Global models using decision tree algorithms. (a) Decision trees assessment within
the interior subregion; (b) Decision trees assessment within the exterior subregion.
total from 4000 to 30000 points; the exact same points
are used in the corresponding Global models. Fifty dif-
ferent decision trees are produced for each training size.
This process minimizes the bias regarding the random-
ness of training set selection. Moreover, a line connect-
ing the maximum value of Kappa and accuracy percent-

D. TRIANTAKONSTANTIS ET AL. 204
age for each training size is drawn.
The comparison within the interior subregion using
models Localint and Globalint for both Kappa and accu-
racy percentage in different training sizes is given in
Figure 5(a). The comparison in the exterior subregion
between Localext and Globalext is presented in Figure
5(b). In the interior subregion, the Localint model exhibits
significant improvements over the Globalint, while the
results for the exterior subregion do not show sign ificant
differe nc es b etween the Localext and Globalext models.
4.2. Entire Region Performance Assessment
4.2.1. Singl e Pixel Assessme nt
Using the subregion performance assessment we fuse the
Local Interior model (Localint) with the Global Exterior
model (Globalext) to formulate the proposed SHEB model.
The SHEB is then compared to a decision tree-based
Global model (Globalall) operating on the entire study
area. Since both SHEB and Global model use the same
model to classify points in the exterior subregion, algo-
rithmic improvements are due to any performance differ-
ences in the interior subregion. W e average improveme nt s
over both regions to produce the overall accuracy and
Kappa statistics comparisons of Figure 6. It is worth
mentioning t hat i n decisi on t ree grap hs (Figures 5 and 6),
both Kappa and accuracy percentage are sensitive to the
number of training points, as expected. In order to ex-
amine the significance of Kappa statistic as well as the
accuracy percentage in the two pairwise comparisons
(SHEB VS Globalall), a paired Student’s t-test is carried
out. The comparison aggregates differences between the
best two models for each training dataset size. This test is
used to investigate performance relationship between
two models, without considering any one-to-one corre-
spondence between poin ts belonging into the same group.
According to Table 1, SHEB model differences from the
Global model in terms of both Kappa and accuracy per-
centages are statistically significant (a=0.05). In addition,
the negative t values for the exterior subregio n justify the
selection of the Global over the Local model to partici-
pate in the SHEB model.
4.2.2. Neig hborhood Asses sment
The above accuracy metrics are based on a pixel per
pixel comparison between model output and reference
data. Multi-scale accuracies are also used to aggregate
performance within a neighborhood moving away from
individual pixels. The multi-scale accuracies capture the
similarity of patterns providing an assessment in differ-
ent resolutions. More specifically, the multi-scale accu-
racy assesses the number of changes occurred in a speci-
fied window versus the actual number of changes with-
out taking into account the exact spatial specificity of
these changes as long as they take place within a local
neighborhood. This assessment technique is important
and beneficial for potential users such as policy makers
and planners, where algorithmic performance in a given
window (e.g. a 1 mile block) is more desirable rather
than the actual locations of urban sprawl within that
neighborhood. The calculation is defined by the follow-
ing form ul a [79].
,
,
1,
,
1id
nid
iid
id
mm
M
Fn





where ,id
F
is the accuracy of the pixel i in a window
with d diameter size of the circular window within which
the accuracy is calculated, is the actual changes
occurred in d,
,id
m
,id
m is the predicted changes in d, ,id
M
is the total valid pixels (excluding the existing urban de-
veloped pix els in 1977) in the examined window and n is
the total population of pixels.
In Figure 7, the graphs of multi-scale accuracies are
presented using the training sets of 4000, 16000 and
30000 points for both SHEB and Globalall models. For
each training size test, the best algorithm of the 50 deci-
sion trees was selected in order to calculate the
multi-scale accuracies. The size of neighborhood ranges
from 3x3 to 70x70 pixels (90m to 2100m). The fusion
between Localint and Globalext (SHEB model) offers in-
creased accuracy when compared to the Globalall model.
For example, at the 1km scale, a representative planning
scale for the urban community, accuracy improvement
varies from 1% to 3%. Most importantly, improvements
are more significant for smaller training set sizes, which
makes the proposed method even more appealing con-
sidering that data availability is a typical limitation in
such models.
5. Discussion and Conclusions
A Spatially Heterogeneous Expert Based (SHEB) model,
which addresses spatial heterogeneity using multiple
region-specific models, is introduced in this research.
Our hypothesis investigates whether expert knowledge
improves prediction accuracy through model regionali-
zation, in other words whether the integration of different
models in homogeneous local subregions outperforms a
global model trained in the entire study area. Most simi-
lar studies capture the spatial heterogeneity using the
differentiated factor, the factor which describes this dis-
similarity, as an additional term to a global model ap-
plied in the entire study area. In contrast, the SHEB
model uses this expert knowledge prior to the model ap-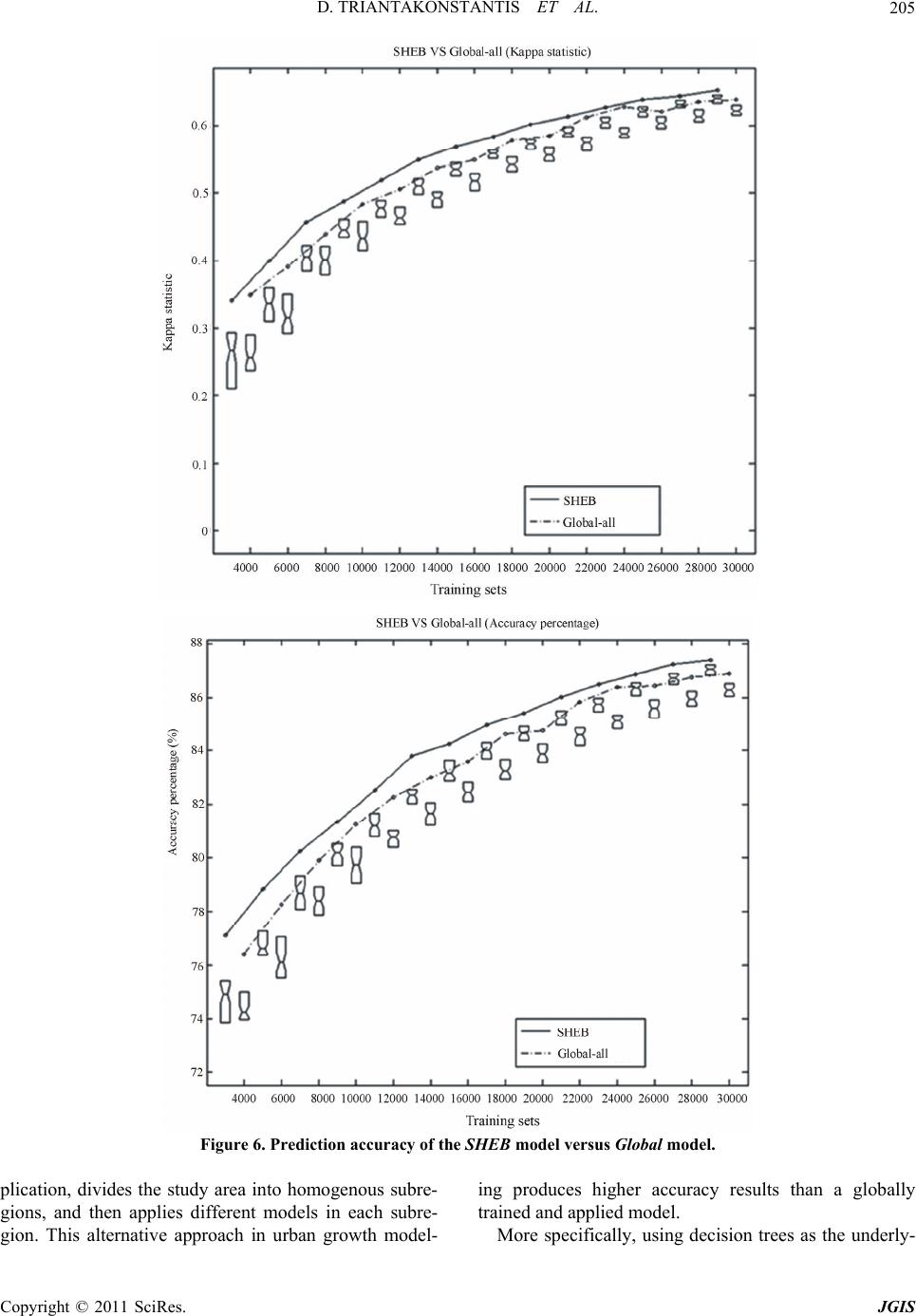

D. TRIANTAKONSTANTIS ET AL. 205
Figure 6. Prediction accuracy of the SHEB model versus Global model.
plication, divides the study area into homogenous subre-
gions, and then applies different models in each subre-
gion. This alternative approach in urban growth model-
ing produces higher accuracy results than a globally
trained and applied model.
More specifically, using decision trees as the underly-
C
opyright © 2011 SciRes. JGIS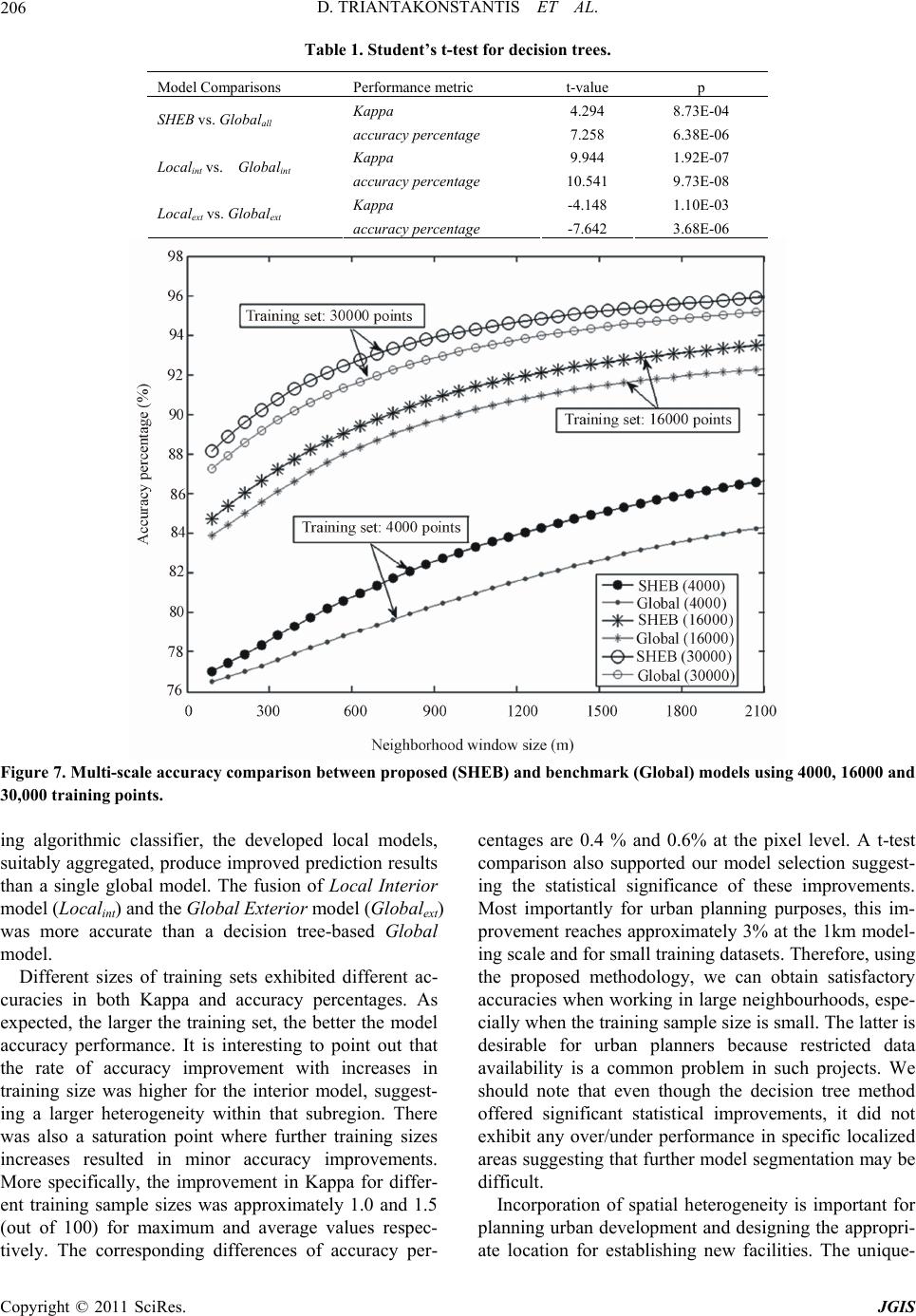

D. TRIANTAKONSTANTIS ET AL. 206
Table 1. Student’s t-test for decision trees.
Model Comparisons Performance metric t-value p
Kappa 4.294 8.73E-04
SHEB vs. Globalall accuracy percentage 7.258 6.38E-06
Kappa 9.944 1.92E-07
Localint vs. Globalint accuracy percentage 10.541 9.73E-08
Kappa -4.148 1.10E-03
Localext vs. Globalext accuracy percentage -7.642 3.68E-06
Figure 7. Multi-scale accuracy comparison between proposed (SHEB) and benchmark (Global) models using 4000, 16000 and
30,000 training points.
ing algorithmic classifier, the developed local models,
suitably aggregated, produce improved prediction results
than a single global model. The fusion of Local Interior
model (Localint) and the Global Exterior model (Globalext)
was more accurate than a decision tree-based Global
model.
Different sizes of training sets exhibited different ac-
curacies in both Kappa and accuracy percentages. As
expected, the larger the training set, the better the model
accuracy performance. It is interesting to point out that
the rate of accuracy improvement with increases in
training size was higher for the interior model, suggest-
ing a larger heterogeneity within that subregion. There
was also a saturation point where further training sizes
increases resulted in minor accuracy improvements.
More specifically, the improvement in Kappa for differ-
ent training sample sizes was approximately 1.0 and 1.5
(out of 100) for maximum and average values respec-
tively. The corresponding differences of accuracy per-
centages are 0.4 % and 0.6% at the pixel level. A t-test
comparison also supported our model selection suggest-
ing the statistical significance of these improvements.
Most importantly for urban planning purposes, this im-
provement reaches approximately 3% at the 1km model-
ing scale and for small training datasets. Therefore, using
the proposed methodology, we can obtain satisfactory
accuracies when working in large neighbourhoods, espe-
cially when the training sample size is small. The latter is
desirable for urban planners because restricted data
availability is a common problem in such projects. We
should note that even though the decision tree method
offered significant statistical improvements, it did not
exhibit any over/under performance in specific localized
areas suggesting that further model segmentation may be
difficult.
Incorporation of spatial heterogeneity is important for
planning urban development and designing the appropri-
ate location for establishing new facilities. The unique-
C
opyright © 2011 SciRes. JGIS

D. TRIANTAKONSTANTIS ET AL.207
ness of a subregion can be identified not only by charac-
teristics on its spatial and morphological properties, but
also based on socioeconomic factors which may be im-
plicitly present in these spatial representations. An inter-
esting future investigation could base model regionaliza-
tion on socioeconomic and administrative variables. For
example, different models could be based on governing
units that inherently may behave differently. The local
information can provide reliable modeling adaptability
because expert knowledge can more easily be incorpo-
rated in homogenous subregions rather than in the entire
study area. The SHEB model can sufficiently support the
applicability of different homogenous subregion extrac-
tions, in order to handle the spatial heterogeneity. The
usage of interior and exterior subregions in the present
study acts as a proof of concept. In troducing further spa-
tial heterogeneity into th e model could po tentially lead to
further improvements in the prediction accuracy of urban
development.
6. Acknowledgements
This research was supported by the Nation al Aeronautics
and Space Administration through an award for Dr.
Mountrakis from the New Investigator Progra m (award #
NNX08AR11G).
7. References
[1] United Nations Population Fund, “State of the World
Population 2007: Unleashing the Potential of Urban
Growth,” United Nations Population Fund, United Na-
tions Publications, 2007.
[2] United Nations Population Fund, “The State of World
Population,” United Nations Population Fund, United
Nations Publications, 1999.
[3] A. Rahman, Y. Kumar, S. Fazal and S. Bhaskaran, “Ur-
banization and Quality of Urban Environment Using
Remote Sensing and GIS Techniques in East Delhi-In-
dia,” Journal of Geographic Information System, Vol. 3,
No. 1, 2011, pp. 62-84. doi:10.4236/jgis.2011.31005
[4] R. M. Mendes and R. Lorandi, “Geospatial Analysis of
Geotechnical Data Applied to Urban Infrastructure Plan-
ning,” Journal of Geographic Information System, Vol. 2,
No. 1, 2010, pp. 23-31. doi:10.4236/jgis.2010.21006
[5] H. Briassoulis, “Analysis of Land Use Change: Theoreti-
cal and Modeling Approaches,” West Virginia University:
Regional Research Institute, Morgantown, 2000.
http://www.rri.wvu.edu/WebBook/Briassoulis/contents.ht
m
[6] J. I. Barredo, M. Kasanko, N. Mccormick and C. Lavalle,
“Modelling Dynamic Spatial Processes: Simulation of
Urban Future Scenarios through Cellular Automata,”
Landscape and Urban Planning, Vol. 64, No. 3, 2003,
pp.145-160. doi:10.1016/S0169-2046(02)00218-9
[7] Veldkamp and P. H. Verburg, “Modelling Land Use
Change and Environmental Impact,” Journal of environ-
mental management, Vol. 72, No. 1-2, 2004, pp. 1-3.
doi:10.1016/j.jenvman.2004.04.004
[8] M. Batty, “Agents, Cells, and Cities: New Representa-
tional Models for Simulating Multiscale Urban Dynam-
ics,” Environment and Planning A, Vol. 37, No. 8, 2005,
pp. 1373-1394. doi:10.1068/a3784
[9] P. H. Verburg and A. Veldkamp, “Introduction to the
Special Issue on Spatial Modeling to Explore Land Use
Dynamics,” International Journal of Geographical In-
formation Science, Vol. 19, No. 2, 2005, pp. 99-102.
doi:10.1080/13658810410001713362
[10] J. Wu and R. Hobbs, “Key Issues and Research Priorities
in Landscape Ecology: An Idiosyncratic Synthesis,”
Landscape Ecology, Vol. 17, No. 4, 2002, pp. 355-365.
doi:10.1023/A:1020561630963
[11] E. G. Irwin, “New Directions for Urban Economic Mod-
els of Land Use Change: Incorporating Spatial Dynamics
and Heterogeneity,” Journal of Regional Science, Vol. 50,
No. 1, 2010, pp. 65-91.
doi:10.1111/j.1467-9787.2009.00655.x
[12] J. R. Eastman, L. A. Solorzano and M. E. Van Fossen,
“Transition Potential Modeling for Land-Cover Change,”
In: D. J. Maguire, M. Batty and M. F. Goodchild, Eds.,
GIS, Spatial Analysis, and Modeling, ESRI Press, Red-
lands, 2005, pp. 357-385.
[13] J. R. Eastman, “Idrisi Kilimanjaro, Manual,” Clark Labs,
Clark University, Worcester, 2003.
[14] R. Aspinall, “Modelling Land Use Change with General-
ized Linear Models—A Multi-Model Analysis of Change
between 1860 and 2000 in Gallatin Valley, Montana,”
Journal of environmental management, Vol. 72, No. 1-2,
2004, pp. 91-103. doi:10.1016/j.jenvman.2004.02.009
[15] Sebastian-Lopez, R. Salvador-Civil, J. Gonzalo-Jimenez
and J. Sanmiguel-Ayanz, “Integration of Socio-Economic
and Environmental Variables for Modelling Long-Term
Fire Danger in Southern Europe,” European Journal of
Forest Research, Vol. 127, No. 2, 2008, pp. 149-163.
doi:10.1007/s10342-007-0191-5
[16] J. Allen and K. Lu, “Modeling and Prediction of Future
Urban Growth in the Charleston Region of South Caro-
lina: A GIS-Based Integrated Approach,” Ecology and
Society, Vol. 8, No. 2, 2003, p. 2.
[17] P. H. Verburg, T. C. M. De Nijs, J. Ritsema Van Eck, H.
Visser and K. De Jong, “A Method to Analyse Neigh-
bourhood Characteristics of land Use Patterns,” Com-
puters, Environment and Urban Systems, Vol. 28, No. 6,
2004, pp. 667-690.
doi:10.1016/j.compenvurbsys.2003.07.001
[18] Z. Hu and C. P. Lo, “Modeling Urban Growth in Atlanta
Using Logistic Regression,” Computers, Environment
and Urban Systems, Vol. 31, No. 6, 2007, pp. 667-688.
doi:10.1016/j.compenvurbsys.2006.11.001
[19] B. Huang, L. Zhang and B. Wu, “Spatiotemporal Analy-
sis of Rural-Urban Land Conversion,” International Jour-
nal of Geographical Information Science, Vol. 23, No. 3,

D. TRIANTAKONSTANTIS ET AL. 208
2009, pp. 379-398. doi:10.1080/13658810802119685
[20] N. H. Augustin, M. A. Mugglestone and S. T. Buckland,
“An Autologistic Model for the Spatial Distribution of
Wildlife,” Journal of Applied Ecology, Vol. 33, No. 2,
1996, pp. 339-347. doi:10.2307/2404755
[21] K. P. Overmars, G. H. J. De Koning and A. Veldkamp,
“Spatial Autocorrelation in Multi-Scale Land Use Mod-
els,” Ecological Modelling, Vol. 164, No. 2-3, 2003, pp.
257-270. doi:10.1016/S0304-3800(03)00070-X
[22] C. F. Dormann, “Assessing the Validity of Autologistic
Regression,” Ecological Modelling, Vol. 207, No. 2-4,
2007, pp. 234-242. doi:10.1016/j.ecolmodel.2007.05.002
[23] Getis and D. A. Griffith, “Comparative Spatial Filtering
in Regression Analysis,” Geographical Analysis, Vol. 34,
No. 2, 2002, pp. 130-140.
[24] J. Malczewski, “Ordered Weighted Averaging with
Fuzzy Quantifiers: GIS-Based Multicriteria Evaluation
for Land-Use Suitability Analysis,” International Journal
of Applied Earth Observation and Geoinformation, Vol. 8,
No. 4, 2006, pp. 270-277. doi:10.1016/j.jag.2006.01.003
[25] Gemitzi, V. A. Tsihrintzis, E. Voudrias, C. Petalas and G.
Stravodimos, “Combining Geographic Information Sys-
tem, Multicriteria Evaluation Techniques and Fuzzy
Logic in Siting MSW Landfills,” Environmental Geology,
Vol. 51, No. 5, 2007, pp. 797-811.
doi:10.1007/s00254-006-0359-1
[26] M. Zarghami and F. Szidarovszky, “Fuzzy Quantifiers in
Sensitivity Analysis of OWA Operator,” Computers and
Industrial Engineering, Vol. 54, No. 4, 2008, pp.
1006-1018. doi:10.1016/j.cie.2007.11.012
[27] Q. Yang, X. Li and X. Shi, “Cellular Automata for Simu-
lating Land Use Changes Based on Support Vector Ma-
chines,” Computers and Geosciences, Vol. 34, No. 6,
2008, pp. 592-602. doi:10.1016/j.cageo.2007.08.003
[28] C. Huang, K. Song, S. Kim, J. R. G. Townshend and P.
Davis, “Use of a Dark Object Concept and Support Vec-
tor Machines to Automate Forest Cover Change Analy-
sis,” Remote Sensing of Environment, Vol. 112, No. 3,
2008, pp. 970-985. doi:10.1016/j.rse.2007.07.023
[29] T. Kuemmerle, P. Hostert, V. C. Radeloff, S. Van der
Linden and K. Perzanowski, “Cross-Border Comparison
of Post-Socialist Farmland Abandonment in the Carpa-
thians,” Ecosystems, Vol. 11, No. 4, 2008, pp. 614-628.
doi:10.1007/s10021-008-9146-z
[30] D. E. Goldberg, “Neighborhood Competition in an
Old-Field Plant Community,” Ecology, Vol. 68, No. 5,
1987, pp. 1211-1223. doi:10.2307/1939205
[31] P. J. Burton, “Some Limitations Inherent to Static Indices
of Plant Competition,” Canadian Journal of Forest Re-
search, Vol. 23, No. 10, 1993, pp. 2141-2152.
doi:10.1139/x93-267
[32] W. D'amato and K. J. Puettmann, “The Relative Domi-
nance Hypothesis Explains Interaction Dynamics in
Mixed Species Alnus Rubra/Pseudotsuga Menziesii
Stands,” Journal of Ecology, Vol. 92, No. 3, 2004, pp.
450-463. doi:10.1111/j.0022-0477.2004.00888.x
[33] S. W. Simard and B. J. Zimonick, “Neighborhood Size
Effects on Mortality, Growth and Crown Morphology of
Paper Birch,” Forest Ecology and Management, Vol. 214,
No. 1-3, 2005, pp. 251-265.
doi:10.1016/j.foreco.2005.04.009
[34] C. He, N. Okada, Q. Zhang, P. Shi and J. Li, “Modelling
Dynamic Urban Expansion Processes Incorporating a
Potential Model with Cellular Automata,” Landscape and
Urban Planning, Vol. 86, No. 1, 2008, pp. 79-91.
doi:10.1016/j.landurbplan.2007.12.010
[35] S. J. Walsh, J. P. Messina, C. F. Mena, G. P. Malanson
and P. H. Page, “Complexity Theory, Spatial Simulation
Models, and Land Use Dynamics in the Northern Ecua-
dorian Amazon,” Geoforum, Vol. 39, No. 2, 2008, pp.
867-878. doi:10.1016/j.geoforum.2007.02.011
[36] Menard and D. J. Marceau, “Simulating the Impact of
Forest Management Scenarios in an Agricultural Land-
scape of Southern Quebec, Canada, Using a Geographic
Cellular Automata,” Landscape and Urban Planning, Vol.
79, No. 3-4, 2007, pp. 253-265.
doi:10.1016/j.landurbplan.2006.02.016
[37] H. Couclelis, “From Cellular Automata to Urban Models:
New Principles for Model Development and Implementa-
tion,” Environment and Planning B: Planning and Design,
Vol. 24, No. 2, 1997, pp. 165-174.
doi:10.1068/b240165
[38] R. White and G. Engelen, “High-Resolution Integrated
Modelling of the Spatial Dynamics of Urban and Re-
gional Systems,” Computers, Environment and Urban
Systems, Vol. 24, No. 5, 2000, pp. 383-400.
doi:10.1016/S0198-9715(00)00012-0
[39] X. Liu, X. Li, L. Liu, J. He and B. Ai, “A Bottom-Up
Approach to Discover Transition Rules of Cellular Auto-
mata Using Ant Intelligence,” International Journal of
Geographical Information Science, Vol. 22, No. 11-12,
2008, pp. 1247-1269. doi:10.1080/13658810701757510
[40] J. V. Vliet, R. White and S. Dragicevic, “Modeling Urban
Growth Using a Variable Grid Cellular Automaton,”
Computers, Environment and Urban Systems, Vol. 33,
No. 1, 2009, pp. 35-43.
doi:10.1016/j.compenvurbsys.2008.06.006
[41] F. Del Frate, F. Pacifici, G. Schiavon and C. Solimini,
“Use of Neural Networks for Automatic Classification
from High-Resolution Images,” IEEE Transactions on
Geoscience and Remote Sensing, Vol. 45, No. 4, 2007, pp.
800-809. doi:10.1109/TGRS.2007.892009
[42] M. J. Canty, “Boosting a Fast Neural Network for Super-
vised Land Cover Classification,” Computers and Geo-
sciences, Vol. 35, No. 6, 2009, pp. 1280-1295.
doi:10.1016/j.cageo.2008.07.004
[43] T. Kavzoglu, “Increasing the Accuracy of Neural Net-
work Classification Using Refined Training Data,” Envi-
ronmental Modelling Software, Vol. 24, No. 7, 2009, pp.
850. doi:10.1016/j.envsoft.2008.11.012
[44] JR. R. G. Pontius, W. Boersma, J. Castella, K. Clarke and
T. Nijs, “Comparing the input, output, and Validation
Maps for Several Models of Land Change,” Annals of
Regional Science, Vol. 42, No. 1, 2008, pp. 11-37.
doi:10.1007/s00168-007-0138-2

D. TRIANTAKONSTANTIS ET AL.209
[45] T. Lakes, D. Muller and C. Kruger, “Cropland Change in
Southern Romania: A Comparison of Logistic Regres-
sions and Artificial Neural Networks,” Landscape Ecol-
ogy, Vol. 24, No. 9, 2009, pp. 1195-1206.
doi:10.1007/s10980-009-9404-2
[46] B. C. Pijanowski, A. Tayyebi, M. R. Delavar and M. J.
Yazdanpanah, “Urban Expansion Simulation Using Geo-
spatial Information System and Artificial Neural Net-
works,” International Journal of Environmental Research,
Vol. 3, No. 4, 2009, pp. 493-502.
[47] B. C. Pijanowski, D. G. Brown, B. A. Shellito and G. A.
Manik, “Using Neural Networks and GIS to Forecast
Land Use Changes: A Land Transformation Model,”
Computers, Environment and Urban Systems, Vol. 26,
No. 6, 2002, pp. 553-575.
doi:10.1016/S0198-9715(01)00015-1
[48] C. E. Rizkalla and R. K. Swihart, “Forecasting the Effects
of Land-Use Change on Forest Rodents in Indiana,” En-
vironmental Management, Vol. 44, No. 5, 2009, pp.
899-908.
[49] W. Liu and K. C. Seto, “Using the ART-MMAP neural
Network to Model and Predict Urban Growth: A Spatio-
temporal Data Mining Approach,” Environment and
Planning B: Planning and Design, Vol. 35, No. 2, 2008,
pp. 296-317. doi:10.1068/b3312
[50] X. Li and A. G. Yeh, “Calibration of Cellular Automata
by Using Neural Networks for the Simulation of Com-
plex Urban Systems,” Environment and Planning A, Vol.
33, No. 8, 2001, pp. 1445-1462. doi:10.1068/a33210
[51] Y. Mahajan and P. Venkatachalam, “Neural Network
Based Cellular Automata Model for Dynamic Spatial
Modeling in GIS,” Lecture Notes in Computer Science
(Including Subseries Lecture Notes in Artificial Intelli-
gence and Lecture Notes in Bioinformatics), Vol. 5592,
Part 1, 2009, pp. 341-352.
[52] B. C. Pijanowski, S. Pithadia, B. A. Shellito and K. Al-
exandridis, “Calibrating a Neural Network-Based Urban
Change Model for Two Metropolitan Areas of the Upper
Midwest of the United States,” International Journal of
Geographical Information Science, Vol. 19, No. 2, 2005,
pp. 97-215. doi:10.1080/13658810410001713416
[53] Q. Guan, L. Wang and K. C. Clarke, “An Artificial-
Neural-Network-Based, Constrained CA Model for Si-
mulating Urban Growth,” Cartography and Geographic
Information Science, Vol. 32, No. 4, 2005, pp. 369-380.
doi:10.1559/152304005775194746
[54] C. M. Almeida, J. M. Gleriani, E. F. Castejon and B. S.
Soares-Filho, “Using Neural Networks and Cellular
Automata for Modelling Intra-Urban Land-Use Dynam-
ics,” International Journal of Geographical Information
Science, Vol. 22, No. 9, 2008, pp. 943-963.
[55] J. C. Chan, K. Chan and A. G. Yeh, “Detecting the Na-
ture of Change in an Urban Environment: A Comparison
of Machine Learning Algorithms,” Photogrammetric En-
gineering and Remote Sensing, Vol. 67, No. 2, 2001, pp.
213-225.
[56] X. Li and C. Claramunt, “A Spatial Entropy-Based Deci-
sion Tree for Classification of Geographical Informa-
tion,” Transactions in GIS, Vol. 10, No. 3, 2006, pp.
451-467. doi:10.1111/j.1467-9671.2006.01006.x
[57] X. Liu, X. Li, X. Shi, S. Wu and T. Liu, “Simulating
Complex Urban Development Using Kernel-Based Non-
Linear Cellular Automata,” Ecological Modelling, Vol.
211, No. 1-2, 2008, pp. 169-181.
doi:10.1016/j.ecolmodel.2007.08.024
[58] X. Li and A. G. Yeh, “Analyzing Spatial Restructuring of
Land Use Patterns in a Fast Growing Region Using Re-
mote Sensing and GIS,” Landscape and Urban Planning,
Vol. 69, No. 4, 2004, pp. 335-354.
doi:10.1016/j.landurbplan.2003.10.033
[59] S. E. Sesnie, P. E. Gessler, B. Finegan and S. Thessler,
“Integrating Landsat TM and SRTM-DEM Derived Vari-
ables with Decision Trees for Habitat Classification and
Change Detection in Complex Neotropical Environ-
ments,” Remote Sensing of Environment, Vol. 112, No. 5,
2008, pp. 2145-2159. doi:10.1016/j.rse.2007.08.025
[60] J. R. Quinlan, “Probabilistic Decision Tress,” In: K. Yves
and R. Michalski, Eds., Machine Learning: An Artificial
Intelligence Approach, Morgan Kaufmann, San Mateo,
Vol. 3, 1983, pp. 140-152.
[61] R. I. McDonald and D. L. Urban, “Spatially Varying
Rules of Landscape Change: Lessons from a Case
Study,” Landscape and Urban Planning, Vol. 74, No. 1,
2006, pp. 7-20. doi:10.1016/j.landurbplan.2004.08.005
[62] J. Liu and W. W. Taylor, “Integrating Landscape Ecology
into Natural Resource Management,” Cambridge Univer-
sity Press, Cambridge, 2002.
doi:10.1017/CBO9780511613654
[63] D. G. Brown, S. Page, R. Riolo, M. Zellner and W. Rand,
“Path Dependence and the Validation of Agent-Based
Spatial Models of Land Use,” International Journal of
Geographical Information Science, Vol. 19, No. 2, 2005,
pp. 153-174. doi:10.1080/13658810410001713399
[64] J. Wang and G. Mountrakis, “Developing a Multi-Net-
work Urbanization (MuNU) Model: A Case Study of Ur-
ban Growth in Denver, Colorado,” International Journal
of Geographical Information Science, Vol. 25, No. 2,
2011, pp. 229-253. doi:10.1080/13658810903473213
[65] M. Raty and A. Kangas, “Localizing General Models
with Classification and Regression Trees,” Scandinavian
Journal of Forest Research, Vol. 23, No. 5, 2008, pp.
419-430. doi:10.1080/02827580802378826
[66] M. Herold, H. Couclelis and K. C. Clarke, “The Role of
Spatial Metrics in the Analysis and Modeling of Urban
Land Use Change,” Computers, Environment and Urban
Systems, Vol. 29, No. 4, 2005, pp. 369-399.
doi:10.1016/j.compenvurbsys.2003.12.001
[67] L. Porter-Bolland, E. A. Ellis and H. L. Gholz, “Land Use
Dynamics and Landscape History in La Montaña, Cam-
peche, Mexico,” Landscape and Urban Planning, Vol. 82,
No. 4, 2007, pp. 198-207.
[68] J. S. Deng, K. Wang, Y, Hong and J. G. Qi, “Spatio-
Temporal Dynamics and Evolution of Land Use Change
and Landscape Pattern in Response to Rapid Urbaniza-
tion,” Landscape and Urban Planning, Vol. 92, No. 3-4,
2009, pp. 187-198.

D. TRIANTAKONSTANTIS ET AL. 210
doi:10.1016/j.landurbplan.2009.05.001
[69] K. McGarigal, S. Tagil and S. A. Cushman, “Surface
Metrics: An Alternative to Patch Metrics for the Quanti-
fication of Landscape Structure,” Landscape Ecology,
Vol. 24, No. 3, 2009, pp. 433-450.
doi:10.1007/s10980-009-9327-y
[70] D. Triantakonstantis and S. Barr, “A Spatial Structural
and Statistical Approach to Building Classification of
Residential Function for City-Scale Impact Assessment
Studies,” Lecture Notes in Computer Science, Vol. 5592,
2009, pp. 221-236. doi:10.1007/978-3-642-02454-2_16
[71] Lagarias, “Fractal Analysis of the Urbanization at the
Outskirts of the City: Models, Measurement and Expla-
nation,” CyberGeo: European Journal of Geography,
2007, pp. 1-16.
[72] S. Barr and M. Barnsley, “A Region-Based, Graph-Theo-
retic Data Model for the Inference of Second-Order The-
matic Information from Remotely-Sensed Images,” In-
ternational Journal of Geographical Information Science,
Vol. 11, No. 6, 1997, pp. 555-576.
doi:10.1080/136588197242194
[73] K. Wu, N. Nunan, J. W. Crawford, I. M. Young and K.
Ritz, “An Efficient Markov Chain Model for the Simula-
tion of Heterogeneous Soil Structure,” Soil Science Soci-
ety of America Journal, Vol. 68, No. 2. 2004, pp. 346-351.
doi:10.2136/sssaj2004.0346
[74] J. Gong, Y. Liu and B. Xia, “Spatial Heterogeneity of
Urban Land-Cover Landscape in Guangzhou from 1990
to 2005,” Journal of Geographical Sciences, Vol. 19, No.
2, 2009, pp. 213-224. doi:10.1007/s11442-009-0213-y
[75] T. G. Wade, J. D. Wickham, N. Zacarelli and K. H. Riit-
ters, “A Multi-Scale Method of Mapping Urban Influ-
ence,” Environmental Modelling & Software, Vol. 24, No.
10, 2009, pp. 1252-1256.
doi:10.1016/j.envsoft.2009.03.006
[76] M. Story and R. G. Congalton, “Accuracy Assessment: A
User’s Perspective,” Photogrammetric Engineering and
Remote Sensing, Vol. 52, No. 3, 1986, pp. 397-399.
[77] R. G. Congalton, “A Review of Assessing the Accuracy
of Classifications of Remotely Sensed Data,” Remote
Sensing of Environment, Vol. 37, No. 1, 1991, pp. 35-46.
doi:10.1016/0034-4257(91)90048-B
[78] J. Cohen, “A Coefficient of Agreement for Nominal
Scales,” Educational and Psychological Measurement,
Vol. 20, No. 1, 1960, pp. 37–46.
doi:10.1177/001316446002000104
[79] R. Costanza, “Model Goodness of Fit: A Multiple Reso-
lution Procedure,” Ecological Modelling, Vol. 47, No.
3-4, 1989, pp. 199-215.
doi:10.1016/0304-3800(89)90001-X