Materials Sciences and Applicatio n, 2011, 2, 749-757
doi:10.4236/msa.2011.27103 Published Online July 2011 (http://www.SciRP.org/journal/msa)
FP-LMTO Investigation of the Structural and
Electronic Properties of CuxAg1–xI Alloys
Mohammed Ameri1*, Noureddine Bouzouira1, Mohammed Doui-Aici2, Rabah Khenata3,4,
Abdelkader Yakoubi5, Boualem Abidri1, Nouredinne Moulay1, Mohammed Maachou1
1Département de Physique, Faculté des Sciences, Université Djillali Liabès, Sidi-Bel-Abbés, Algérie; 2Laboratoire des Matériaux
Appliqués, Centre de Recherche (Ex:CFTE), Route de Mascara, Université de Sidi-Bel-Abbès, Sidi-Bel-Abbès, Algérie; 3Laboratoire
de Physique Quantique et de Modélisation Mathématique de la Matière (LPQ3 M), Université de Mascara, Mascara, Algérie;
4Department of Physics and Astronomy, Faculty of Science, King Saud University, Riyadh, Saudi Arabia; 5Laboratoire Modeling and
Simulation Materials Sciences Laboratory, Sidi-Bel-Abbès University, Sidi-Bel-Abbès,Algeria.
Received December 28th, 2010; revised March 28th, 2011; accepted May 8th, 2011.
ABSTRACT
The structural and electronic properties of the ternary CuxAg1–xI, alloy have been calculated, using the full-potential
linear muffin-tin -orbital (FP-LMTO) method based on density functional theory, within both the local density ap proxi-
mation and the generalized gradient approximation (GGA). The equilibrium lattice constants and the bu lk modulus are
compared with previous theoretical calculations. The concentration dependence of the electronic band structure and
the direct-indirect band gaps is also investigated. Using the approach of Zunger and co-workers the microscopic ori-
gins of the gap bowing were also explained.
Keywords: (FP-LMTO) Method, CuxAg1–xI Alloy
1. Introduction
Silver iodide and copper iodide have received attention
as promising materials for applications in technological
devices and are used as model systems in both physical
and numerical experiments [1]. These compounds which
have four valence electrons per atoms, crystallize in a
tetrahedral coordinated zinc-blende (ZB) structure [2,3]
under ambient conditions. Silver iodide can exist in three
crystal polymorphs at atmospheric pressure. Below 420
K silver iodide crystallizes in the hexagonal β phase
(wurtzite structure). Copper iodide also has several
transformations. The low-temperature cubic γ-CuI phase
with the zinc blende structure, transforms to the β phase
with a distorted hexagonal structure and a rock salt
structure above 673 K (α-CuI). Another interesting fea-
ture of these systems is that the lattice mismatch between
CuI and AgI is very small and therefore it is useful to
combine them for forming CuxAg1–xI alloys. Indeed, CuI
and AgI binary compounds form a continuous series of
alloys (CuxAg1–xI), where 0 < x < 1 denotes the molar
fraction of Cu. Both CuI and AgI crystallizes in the cubic
zinc blende structure. Hence, one would expect that the
different properties of the ternary alloy to be vary smooth-
ly between the end points. Moreover, it was shown ex-
perimentally [4] that the α-CuxAg1–xI based solid solutions
in the quasibinary AgI–CuI system exists over a wide
temperature range. The ionic transport in CuxAg1–xI was
studied by Nölting and co-workers and Kusakabe et al.
[4,5]. They have observed that the electric conductivity
reduced with increasing the copper concentration.
Goldmann [6] reviewed detailed experimental and
theoretical information of the valence and conduction
band states in CuI, and AgI. He proposed a band struc-
ture model which is able to interpret all available ex-
perimental information extracted from optical absorption
spectroscopy, soft X-ray absorption and emission spec-
troscopy. Theoretically, many calculations using the mo-
lecular dynamics simulations [7,8] have been done to
characterize the structural, electronic, and optical proper-
ties of these systems.
Thus our main goal of this work is to study the effect
of increasing concentration of copper on the structural
and electronic properties band structure such as lattice
constant, bulk modulus, band gaps and effective masses
by using the full potential linear muffin-tin orbitals
(FP-LMTO) method. In this work, we have used the
“special quasirandom structures” (SQS) approach of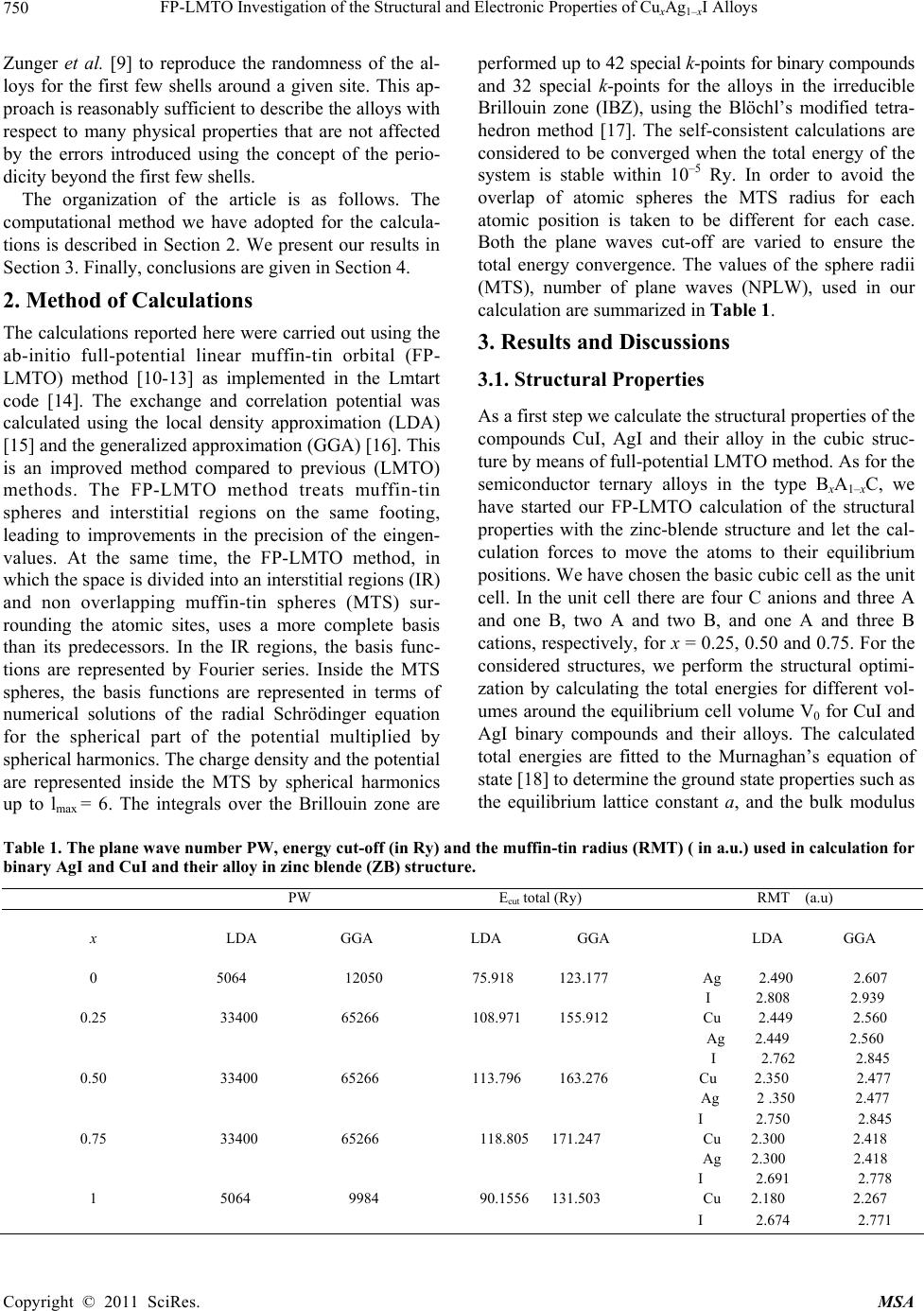

FP-LMTO Investigation of the Structural and Electronic Properties of Cu Ag I Alloys 750 x1–x
Zunger et al. [9] to reproduce the randomness of the al-
loys for the first few shells around a given site. This ap-
proach is reasonably sufficient to describe the alloys with
respect to many physical properties that are not affected
by the errors introduced using the concept of the perio-
dicity beyond the first few shells.
The organization of the article is as follows. The
computational method we have adopted for the calcula-
tions is described in Section 2. We present our results in
Section 3. Finally, conclusions are given in Section 4.
2. Method of Calculations
The calculations reported here were carried out using the
ab-initio full-potential linear muffin-tin orbital (FP-
LMTO) method [10-13] as implemented in the Lmtart
code [14]. The exchange and correlation potential was
calculated using the local density approximation (LDA)
[15] and the generalized approximation (GGA) [16]. This
is an improved method compared to previous (LMTO)
methods. The FP-LMTO method treats muffin-tin
spheres and interstitial regions on the same footing,
leading to improvements in the precision of the eingen-
values. At the same time, the FP-LMTO method, in
which the space is divided into an interstitial regions (IR)
and non overlapping muffin-tin spheres (MTS) sur-
rounding the atomic sites, uses a more complete basis
than its predecessors. In the IR regions, the basis func-
tions are represented by Fourier series. Inside the MTS
spheres, the basis functions are represented in terms of
numerical solutions of the radial Schrödinger equation
for the spherical part of the potential multiplied by
spherical harmonics. The charge density and the potential
are represented inside the MTS by spherical harmonics
up to lmax = 6. The integrals over the Brillouin zone are
performed up to 42 special k-points for binary compounds
and 32 special k-points for the alloys in the irreducible
Brillouin zone (IBZ), using the Blöchl’s modified tetra-
hedron method [17]. The self-consistent calculations are
considered to be converged when the total energy of the
system is stable within 10–5 Ry. In order to avoid the
overlap of atomic spheres the MTS radius for each
atomic position is taken to be different for each case.
Both the plane waves cut-off are varied to ensure the
total energy convergence. The values of the sphere radii
(MTS), number of plane waves (NPLW), used in our
calculation are summarized in Table 1.
3. Results and Discussions
3.1. Structural Properties
As a first step we calculate the structural properties of the
compounds CuI, AgI and their alloy in the cubic struc-
ture by means of full-potential LMTO method. As for the
semiconductor ternary alloys in the type BxA1–xC, we
have started our FP-LMTO calculation of the structural
properties with the zinc-blende structure and let the cal-
culation forces to move the atoms to their equilibrium
positions. We have chosen the basic cubic cell as the unit
cell. In the unit cell there are four C anions and three A
and one B, two A and two B, and one A and three B
cations, respectively, for x = 0.25, 0.50 and 0.75. For the
considered structures, we perform the structural optimi-
zation by calculating the total energies for different vol-
umes around the equilibrium cell volume V0 for CuI and
AgI binary compounds and their alloys. The calculated
total energies are fitted to the Murnaghan’s equation of
state [18] to determine the ground state properties such as
the equilibrium lattice constant a, and the bulk modulus
Table 1. The plane wave number PW, energy cut-off (in Ry) and the muffin-tin radius (RMT) ( in a.u.) used in calculation for
binary AgI and CuI and their alloy in zinc blende (ZB) structure.
PW Ecut total (Ry) RMT (a.u)
x LDA GGA LDA GGA LDA GGA
0 5064 12050 75.918 123.177 Ag 2.490 2.607
I 2.808 2.939
0.25 33400 65266 108.971 155.912 Cu 2.449 2.560
Ag 2.449 2.560
I 2.762 2.845
0.50 33400 65266 113.796 163.276 Cu 2.350 2.477
Ag 2 .350 2.477
I 2.750 2.845
0.75 33400 65266 118.805 171.247 Cu 2.300 2.418
Ag 2.300 2.418
I 2.691 2.778
1 5064 9984 90.1556 131.503 Cu 2.180 2.267
I 2.674 2.771

FP-LMTO Investigation of the Structural and Electronic Properties of Cu Ag I Alloys 751
x1–x
B. The calculated equilibrium parameters (a and B) are
given in Table 2 which also contains results of previous
calculations as well as the experimental data. On the
whole, our calculated structural parameters are in good
agreement with those obtained by first-principles meth-
ods within different approximations. The calculated lat-
tice parameters values for the binary compounds are in
good agreement with the measured data, which ensure
the reliability of the present first-principles computations.
The computed lattice parameters slightly underestimates
and overestimates the measured data by using LDA and
GGA, respectively, which are consistent with the general
trend of these approximations. As it can be seen that the
calculated lattice parameter for CuI (x = 1) is smaller
than those of AgI (x = 0); a0 (CuI) < a0 (AgI). As the
anion atom is the same in both compounds, this result
can be easily explained by considering the atomic radii of
Cu and Ag: R(Cu) = 1.35 Å, R(Ag) = 1.60 Å, i.e., the
lattice constant increases with increasing atomic size of
the cation element. The bulk modulus value for CuI is
larger than those of AgI; B (CuI) > B (AgI); i.e., in in-
verse sequence to a0—in agreement with the well-known
relationship between B and the lattice constants:
, where 0 is the unit cell volume. Furthermore,
the values of the calculated bulk modulus using both ap-
proximations decreases from CuI to AgI, suggesting that
the compressibility increases from CuI to AgI.
1
0
BV

V
Usually, in the treatment of alloys when the experi-
mental data are scare, it is assumed that the atoms are
located at the ideal lattice sites and the lattice constant
varies linearly with composition x according to the so-
called Vegard’s law [19].
 
1
1
x
xAC
aABC xaxa
 BC
(1)
where AC and BC are the equilibrium lattice con-
stants of the binary compounds AC and BC respectively,
(AxB1–xC) is the alloy lattice constant. However, vio-
a a
a
lation of Vegard’s law has been observed in semiconduc-
tor alloys both experimentally [20] and theoretically [21].
Hence, the lattice constant can be written as:

  
1
1 1
x xACBC
aABCxaxaxxb
  (2)
where the quadratic term b is the bowing parameter.
Figures 1 and 2, show the variation of the calculated
equilibrium lattice constants and the bulk modulus versus
concentration x for CuxAg1–xI alloy. The obtained results
for the composition dependence of the calculated equi-
librium lattice parameter show an excellent agreement to
Vegard’s law [19]. In going from AgI to CuI; when the
Cu-content increases, the values of the lattice parameters
of the CuxAg1–xI alloy decrease. This is due to the fact
that the size of the Cu atom is smaller than those of Ag
atom. Oppositely, one can see from Figure 2 that the
value of the bulk modulus increases with increasing Cu
concentration. The values of the bowing parameters are
determined by a polynomial fit. Using the LDA ap-
proximation, we obtained upward and downward bowing
parameters equal to –0.11543 Å and 0.01143 GPa for the
lattice and the bulk modulus, respectively. The GGA
approximation gave values of –0.11543 Å and 13.95429
GPa for the bowing lattice parameter and the bulk mod-
ulus, respectively. In view of Table 2, it is clear that both
approximations follow the tendency demonstrated by
both experimental measurement and theoretical calcula-
tions. To the best of our knowledge, there are no experi-
mental work exploring the structural properties (e.g.; the
bulk modulus B and it pressure derivatives B') and the
bowing parameters of the investigated alloys, but our
results are relatively close to those of Ref. [22] obtained
by using the full potential-linear augmented plane wave
(FP-LAPW) method.
3.2. Electronic Properties
The energy band gaps of the binary compounds as well
Table 2. Calculated lattice parameter a and bulk modulus B compared to experimental and other theoretical values of CuI
and AgI and their alloys.
Lattice constant a (Ǻ) Bulk modulus B (Gpa)
this work. expt. other calc. this work. expt. other calc.
LDA GGA LDA GGA
x
0 6.476 6.779 6.499a 6.650c, 6.61d, 6.872e 34.26 23.82 24j 26.667c, 40l
0.25 6.37 6.646 6.516c, 6,39f, 6.38g 37.93 24.7 27.405c, 20,3f, 26.0g
0.5 6.234 6.505 6.396c, 6.31f, 6.30g 42.2 26.61 30,104c, 23f, 27g
0.75 6.101 6.352 6.256c, 6.19f, 6.18g 45.58 29.55 37.765c, 27f, 28g
1 5.943 6.175 6.054b 6.098c, 6.097h, 6.082i 49.7 36.02 36.6b, 31k 38.872c, 39.447h, 39.7i, 35.2m
aRef. [29]; bRef. [30]; cRef. [22]; dRef. [31]; eRef. [32]; fRef. [7]; gRef. [33]; hRef. [34]; iRef. [35]; jRef. [36]; kRef. [37]; lRef. [38]; mRef. [39].

FP-LMTO Investigation of the Structural and Electronic Properties of Cu Ag I Alloys 752 x1–x
6.8
6.7
6.6
6.5
6.4
6.3
6.2
6.1
6.0
5.9 0.0 0.2 0.4 0.6 0.8 1.0
Figure 1. Composition dependence of the calculated lattice constants within LDA (Solid Circle) and GGA (Solid Triangle) of
CuxAg1–xI alloy compared with Vegard’s prediction (doted line).
0.0 0.2 0.4 0.6 0.8 1.0
Figure 2. Composition dependence of the calculated bulk modulus within GGA (Solid Circle) and LDA (Solid Square) of
CuxAg1–xI alloy.
as for their investigated alloy were calculated within the
LDA and GGA schemes. In Table 3 we show the ob-
tained results for the energy band gap of the CuxAg1<-xI
alloy from our ab initio calculations for different values
of the concentration x. These values correspond to 25, 50,
75 and 100 % CuI and AgI substitution, respectively. The
exact value of the band-gap is obviously a crucial point
to be addressed because it enters in the applications in
technological devices. However, it can be seen from
Table 3 that there is a large discrepancy between the
reported experimental and theoretical values. This dis-
crepancy is mainly due to the fact that both the simple
form of LDA or GGA do note take into account the qua-
siparticle self energy correctly [23] which make them
not sufficiently flexible to accurately reproduce both
exchange and correlation energy and its charge deriva-
tive. We worth also mention that in general, it is far to
say that the experimental data are well reproduced by
the calculation. On raison for this difference is that in
our calculations we have assumed the crystal to be at T =
0 K and thus do not include contributions from lattice
vibrations that are present at room temperature meas-
urements. It is important to note that the density func-
tional formalism is limited in its validity (see. Ref [24])
and the band structure derived from it cannot be used
directly for comparison with experiment. The variation
of the concentration (x) versus the value of the direct
band gap energy (  is with both LDA and GGA a p-
proximation is shown in Figure 3. It is clearly seen that
the direct energy gap show a non linear variation with
copper concentration. The obtained energy versus con-
centration curve is well fitted by the following quadratic
phenomenological function.

FP-LMTO Investigation of the Structural and Electronic Properties of Cu Ag I Alloys 753
x1–x
Table 3. Calculated direct energy band gap energy (Γ-Γ) of CuxAg1–xI alloys at different Cu concentrations (all values are in
eV).
E
g (eV)
this work. expt other calc.
x LDA GGA
0 1.171 1.416 1.340c, 2.O77c, 1.4b, 0.8d
0.25 1.012 1.106 1.04632c, 1.68286c
0.5 0.979 0.993 0.958c, 1.59617c
0.75 1.020 0.962 0.965c, 1.61436c
1 1.183 1.018 2.95a 1.068
c, 1.764c, 1.077e, 1.118f, 3.10g
aRef. [16]; bRef. [40]; cRef. [22]; dRef. [41]; eRef. [34]; fRef. [35]; gRef. [42].
2.2
2.0
1.8
1.6
1.4
1.2
1.0
0.8
0.6 0.0 0.2 0.4 0.6 0.8 1.0
Figure 3. Calculated direct energy band gap (Γ –Γ) of CuxAg1–xI alloys as a function of Cu concentration using GGA ap-
proximation (solid square-solid line) compared with Ref. 22, using GGA (Open Triangle-doted line) and EVGGA (Open Cir-
cle-doted line).
 
1
gAC BC
Ex xExEbxx 

1 (3)
where EAC and EBC corresponds to the gap of the CuI
and AgI for the CuxAg1–xI alloy.
The obtained results are shown in Figure 3 and are
summarized as follows:


2
12
E1.67 0.810.82
Cu AgIE1.40 1.310.93
xx
x
xLDA
x
x GGA



 

 


(4)
In order to better understand the physical origins of
bowing parameters in AxB1–xC alloys, we follow the pro-
cedure of Bernard and Zunger [25], and decompose the
total bowing parameter b into physically distinct contri-
butions. The overall bowing coefficient at a given aver-
age composition x measures the change in the band gap
according to the formal reaction
   
1
AC1 BC
ACBCx xeq
x
axaABC

 a
(5)
where AC and a
B
C are the equilibrium lattice con-
stants of the binary compounds and is the equilib-
rium lattice constant of the alloy with the average com-
position x.
a
eq
a
The Equation (5) is decomposed into three steps:



  
AC BC
AC BC
aaACaBCa (6)



 
1
AC1 BC
xx

x
axaABC

 a (7)

 
11

x
xxxeq
A
BCa ABCa

 (8)
The first step measures the volume deformation (VD)
effect on the bowing. The corresponding contributions
bVD to the bowing parameter represents the relative re-
sponse of the band structure of the binary compounds AC
and BC to hydrostatic pressure, which here arises from
the change of their individual equilibrium lattice con-
stants to the alloy value a = a(x). The second contribution,
the charge exchange (CE) contribution bCE, reflects the
charge transfer effect which is due to the different (aver-
aged) bonding behavior at the lattice constant a. The fi-
nal step measure changes due to the structural relaxation
(SR) in passing from the unrelaxed to the relaxed alloy
by bSR. Consequently, the total bowing parameter is de-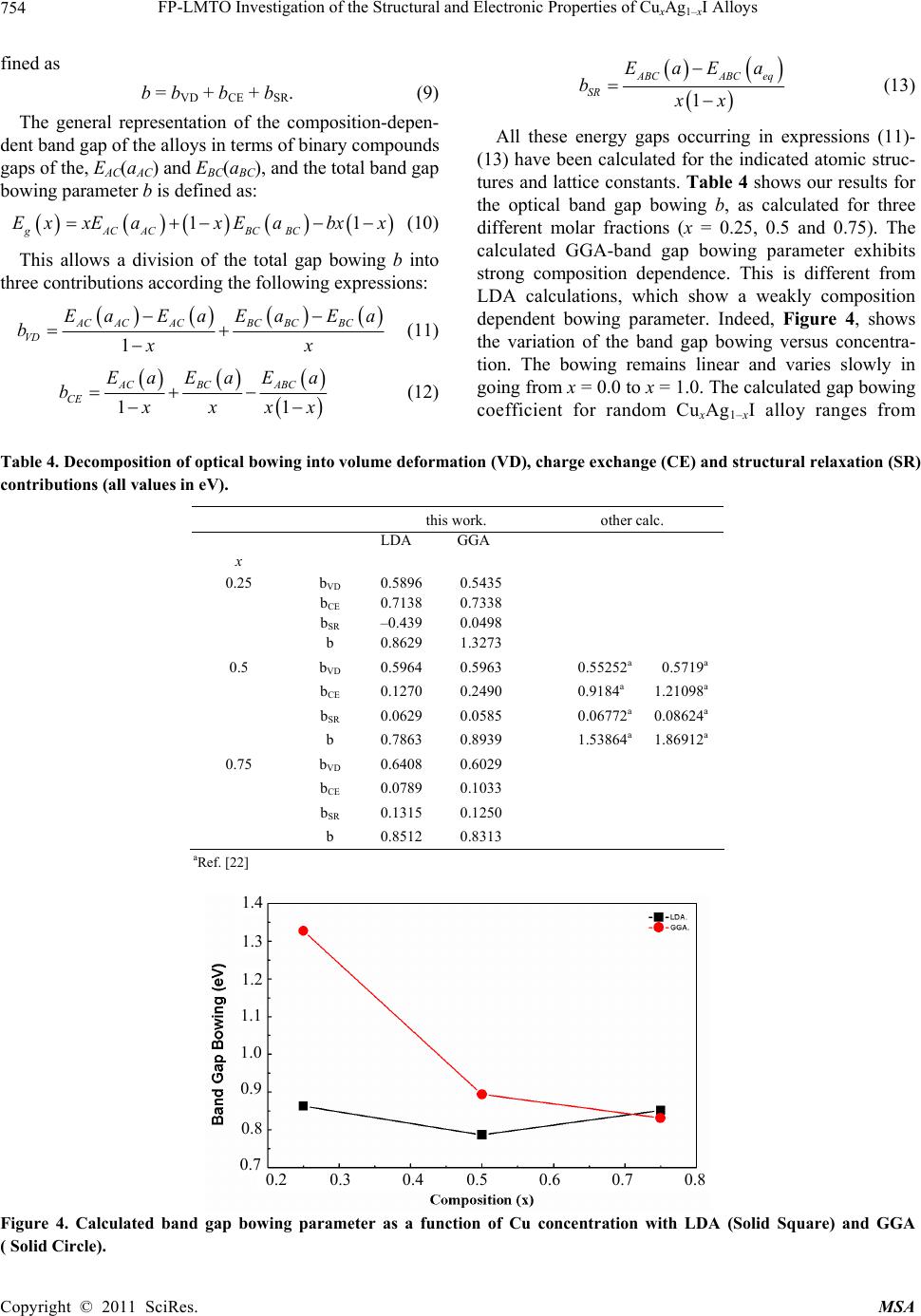

FP-LMTO Investigation of the Structural and Electronic Properties of Cu Ag I Alloys 754 x1–x

1
fined as
b = bVD + bCE + bSR. (9)
The general representation of the composition-depen-
dent band gap of the alloys in terms of binary compounds
gaps of the, EAC(aAC) and EBC(aBC), and the total band gap
bowing parameter b is defined as:
    
1
gACAC BCBC
ExxEaxE abxx  (10)
This allows a division of the total gap bowing b into
three contributions according the following expressions:
   
1
ACACACBC BCBC
VD
EaEaEa Ea
bxx




(11)
  

11
AC BC ABC
CE
EaEaE a
b
x
xxx


(12)

 

1
ABCABC eq
SR
EaEa
bxx

 (13)
All these energy gaps occurring in expressions (11)-
(13) have been calculated for the indicated atomic struc-
tures and lattice constants. Table 4 shows our results for
the optical band gap bowing b, as calculated for three
different molar fractions (x = 0.25, 0.5 and 0.75). The
calculated GGA-band gap bowing parameter exhibits
strong composition dependence. This is different from
LDA calculations, which show a weakly composition
dependent bowing parameter. Indeed, Figure 4, shows
the variation of the band gap bowing versus concentra-
tion. The bowing remains linear and varies slowly in
going from x = 0.0 to x = 1.0. The calculated gap bowing
coefficient for random CuxAg1–xI alloy ranges from
Table 4. Decomposition of optical bowing into volume deformation (VD), charge exchange (CE) and structural relaxation (SR)
contributions (all values in eV).
this work. other calc.
LDA GGA
x
0.25 bVD 0.5896 0.5435
b
CE 0.7138 0.7338
b
SR –0.439 0.0498
b 0.8629 1.3273
0.5 bVD 0.5964 0.5963 0.55252a 0.5719a
b
CE 0.1270 0.2490 0.9184a 1.21098a
b
SR 0.0629 0.0585 0.06772a 0.08624a
b 0.7863 0.8939 1.53864a 1.86912a
0.75 bVD 0.6408 0.6029
b
CE 0.0789 0.1033
b
SR 0.1315 0.1250
b 0.8512 0.8313
aRef. [22]
1.4
1.3
1.2
1.1
1.0
0.9
0.8
0.7 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Figure 4. Calculated band gap bowing parameter as a function of Cu concentration with LDA (Solid Square) and GGA
( Solid Circle).

FP-LMTO Investigation of the Structural and Electronic Properties of Cu Ag I Alloys 755
x1–x
0.8629 eV (x = 0.25) to 0.8512 (x = 0.75). Our result for
x = 0.5 is in excellent agreement with those obtained by
using EVGGA-FPLAPW method [22]. We can also note
that the volume-deformation term bVD of CuxAg1–xI is
large. The importance of bVD can be correlated with the
mismatch of the lattice constants of the corresponding
binary compounds. As consequence, the main contribu-
tion to the gap bowing is raised from the volume defor-
mation effect. The only exception is for x = 0.25 in which
the charge transfer contribution bCE has been found
greater than bVD. This contribution is due to the different
electronegativities of the Ag and Cu or I atoms. Indeed,
bCE scales with the electronegativity mismatch. The con-
tribution of structural relaxation is negligible; the band
gap bowing is due essentially to the charge exchange
effect. We conclude that our calculations show that both
structural (volume deformation) and chemical effects
appear to control the optical gap bowing of CuxAg1–xI
alloy.
3.3. Calculated Effective Masses
Knowledge of the electron and hole effective mass val-
ues is indispensable for the understanding of transport
phenomena, exciton effects and electro-hole in semicon-
ductors. Excitonic properties are of great interest for bi-
nary CuI, AgI and their alloys, therefore, it is worthwhile
to estimate the electron and hole effective mass values
for these materials. Experimentally, the effective masses
are usually determined by cyclotron resonance, electro
reflectance measurements or from analysis of transport
data or transport measurements [43]. Theoretically, the
effective masses can be estimated from the energy band
curvatures. Generally, the effective mass is a tensor with
nine components, however for the much idealized simple
case, where the E-k diagram can be fitted by a parab-
ola 22 *
2Ekm, the effective mass becomes a scalar at
high symmetry point in Brillouin zone. We have com-
puted the electron effective mass at the conduction band
minima (CBM) and the hole effective mass at the valence
band maxima (VBM) for CuI, AgI and their ternary al-
loys. The electron and the hole effective masses are ob-
tained from the curvature of the energy band near the Γ-
point at the conduction band minimum (CBM) and va-
lence band maximum (VBM), respectively. The calcu-
lated electron and hole effective masses values for the
parent binary compounds CuI and AgI and their alloy are
given in Table 5. Results from earlier theoretical works
are also quoted for comparison. The calculated electron
effective masses are in good agreement with those ob-
tained by using the full potential linear augmented plane
wave (FP-LAPW) method whin EVGGA approximation
[22] which is known to improve the values of the band
gaps rather than LDA and GGA [26-28]. This agreement
disappears in the case of hole effective masses. This dis-
agreement could be expected because the computation of
the effective mass is very sensitive to the topology of
band structure. The highest curvature of the electronic
band yields the smallest effective mass of the charge car-
riers and the highest conductivity. Therefore, the effec-
tive masses that depend strongly on the form of energy
band match the expected accuracy. From Table 5 data,
we can outline that holes are much heavier than electrons,
for all concentrations in CuxAg1–xI alloy, so carrier
transport in this alloy should be dominated by electrons.
We notice that no experimental data are available for
effective masses of this alloy; all results are obtained via
theoretical methods. Future experimental work will tes-
tify all calculated results.
4. Conclusions
In summary, by means of the (FP-LMTO) method, we
have calculated the structural and the electronic proper-
ties of zinc-blende CuI, AgI, and their related CuxAg1–xI
alloy. We have found that except the lattice parameter,
the variation of structural parameters versus copper con-
centration not obeys Vegard’s law. Our results of the
electronic band structure show a non linear variation of
the fundamental ban gaps versus copper concentration.
Table 5. The electron and hole effective masses for CuxAg1–xI ternary alloy as function of Cu concentrations using LDA and
GGA. All values are in units of a free-electron mass m0.
me* mhh* m
lh*
this work. other calc. this work. other calc. this work. other calc.
x LDA GGA LDA GGA LDA GGA
0 0.271 0.270 0.226a 0.272a 0.949 0.960 1.818 1.804 1.187a 1.189a
0.25 0.226 0.329 0.197a 0.261a 0.500 0.634 0.524 0.642 1.355a 1.622a
0.50 0.3006 0.306 0.191a 0.256a 0.439 0.577 0.466 0.591 1.281a 1.462a
0.75 0.238 0.285 0.188a 0.251a 0.453 0.5339 0.465 0.541 1.185a 1.318a
1 0.229 0.220 0.186a 0.249a 0.573 0.601 0.804 0.768 1.163a 1.158a
aRef. [22].

FP-LMTO Investigation of the Structural and Electronic Properties of Cu Ag I Alloys 756 x1–x
We have characterized the deviation from the linear be-
havior by calculating the optical bowing parameter. The
effective masses of the systems studied in this work were
calculated and are found comparable to those obtained by
FPLAPW method.
5. Acknowledgements
Author Rabah KHENATA extends his appreciation to
the Deanship of Scientific Research at King Saud Uni-
versity for funding the work through the research group
project N0 RPG-VPP-088
REFERENCES
[1] A. K. Ivanov-Shits and I. V. Murin “Ionika Tverdogo
tela,” Izd-vo SPbGU, S.-Peterburg, 2000.
[2] J. G. P. Binner, G. Dimitrakis, D. M. Price1, M. Reading
and B. Vaidhyanathan, “Hysterisis in the Phase Transition
in Silver Iodide,” Journal of Thermal Analysis and Calo-
rimetry, Vol. 84, No. 2, 2006, pp. 409-412.
doi:10.1007/s10973-005-7154-1
[3] F. Wells, “Structural Inorganic Chemistry,” Oxford Uni-
versity Press, Oxford, 1984.
[4] J. Nölting and Ber. Bunsenges, Physik. Chem., Vol. 68.
No. 10, 1964, p. 932.
[5] M. Kusakabe, Y. Shirakawa, S. Tamaki and Y. Ito, “The
Transport Properties of Cations in the Superionic Phase
of AgxCu1−xI,” Journal of the Physical Society of Japan,
Vol. 64, No. 01, 1995, pp. 170-176.
[6] A. Goldmann, “Band Structure and Optical Properties of
Tetrahedrally Coordinated Cu- and Ag-Halides,” Physica
Status Solidi (B), Vol. 81, No 1, 1977, pp. 9-47.
[7] W. Sekkal, A. Laref and H. Aourag, A. Zaoui and M.
Certier, “The miscibility of CuxAg1−xI Using a Tersoff
Potential,” Superlattice and Microstructures, Vol. 28, No.
1, 2000, pp. 55-66. doi:10.1006/spmi.1999.0782
[8] B. Jarosław and R. Jarosław, “Cation Diffusion Coeffi-
cients in CuAgI via Molecular Dynamics Simulations,”
Solid State Ionics, Vol. 157, No. 1-4, 2003, pp. 227-232.
doi:10.1016/S0167-2738(02)00214-X
[9] A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard,
“Special Quasirandom Structures,” Physical Review Let-
ters, Vol. 65, No. 3, 1990, pp. 353-356.
doi:10.1103/PhysRevLett.65.353
[10] S. Savrasov and D. Savrasov, “Full-Potential Linear-
Muffin-Tin-Orbital Method for Calculating Total Ener-
gies and Forces,” Physical Review B, Vol. 46, No. 19,
1992, pp. 12181-12195.
doi:10.1103/PhysRevB.46.12181
[11] S. Y. Savrasov, “Linear-Response Theory and Lattice
Dynamics: A Muffin-Tin-Orbital Approach,” Physical
Review B, Vol. 54, No. 23, 1996, pp. 16470-16486.
doi:10.1103/PhysRevB.54.16470
[12] P. Hohenberg and W. Kohn, “Inhomogeneous Electron
Gas,” Physical Review, Vol. 136, No. 3B, 1964, pp. B864
-B871.
[13] W. Kohn and L. J. Sham, “Self-Consistent Equations
Including Exchange and Correlation Effects,” Physical
Review A, Vol. 140 , No. 4A, 1965, pp. A1133- A1138.
doi:10.1103/PhysRev.140.A1133
[14] S. Y. Savrasov, “Program LMTART for electronic struc-
ture calculations,” Zeitschrift für Kristallogr, Vol. 220,
2005, pp. 555-557.
[15] J. P. Perdew and Y. Wang, “Accurate and Simple Ana-
lytic Representation of the Electron-Gas Correlation En-
ergy,” Physical Review A, Vol. 45, No. 13, 1992, pp.
13244-13249. doi:10.1103/PhysRevB.45.13244
[16] J. P. Perdew, S. Burke and M. Ernzerhof, “Generalized
Gradient Approximation Made Simple,” Physical Review
Letters, Vol. 77, No.18, 1996, pp. 3865-3868.
doi:10.1103/PhysRevLett.77.3865
[17] P. Blochl, O. Jepsen and O. K. Andersen, “Improved
Tetrahedron Method for Brillouin-Zone Integrations,”
Physical Review B, Vol. 49, No. 23, 1994, pp. 16223-
16233. doi:10.1103/PhysRevB.49.16223
[18] F. D. Murnaghan, “The Compressibility of Media under
Extreme Pressures,” Proceedings of the National Acad-
emy of Sciences USA, Vol. 30, 1944, pp. 244-247.
doi:10.1073/pnas.30.9.244
[19] L. Vegard, “Formation of Mixed Crystals by Solid-Phase
Contact,” Zeitschrift für Phys, Vol. 5, No. 5, 1921, pp.
393-395.
[20] B. Jobst, D. Hommel, U. Lunz, T. Gerharda and G.
Landwehr, “E0 Band-Gap Energy and Lattice Constant of
Ternary Zn1−xMgxSe as Functions of Composition,” Ap-
plied Physics Letters, Vol. 69, No. 1, 1996, pp. 97-100.
doi:10.1063/1.118132
[21] F. El Haj Hassan and H. Akdarzadeh, “First-Principles
Investigation of BNxP1−x, BNxAs1−x and BPxAs1−x Ternary
Alloys,” Materials Science and Engineering, Vol. 121,
2005, pp. 171-178.
[22] B. Amrani, F. El Haj Hassan, R. Khenata and H. Akbar-
zadeh, “Theoretical Study of CuxAg1−xI Alloys,” Journal
of Physics and Chemistry of Solids, Vol. 70, No. 7, 2009,
pp. 1055-1061. doi:10.1016/j.jpcs.2009.05.003
[23] S. N. Rashkeev and W. R. L. Lambrecht, “Second-Har-
monic Generation of I-III-VI2 Chalcopyrite Semiconduc-
tors: Effects of Chemical Substitutions,” Physical Review
B, Vol. 63, No. 16, 2001, pp. 165212-165224.
doi:10.1103/PhysRevB.63.165212
[24] G. Onida, L. Reining, and A. Rubio, “Electronic Excita-
tions: Density-Functional versus Many-Body Green’s-
Function Approaches,” Reviews of Modern Physics, Vol.
74, 2002, pp. 601-659. doi:10.1103/RevModPhys.74.601
[25] J. E. Bernard and A. Zunger, “Optical Bowing in Zinc
Chalcogenide Semiconductor Alloys,” Physical Review B,
Vol. 34 , No. 8, 1986, pp. 5992-5995.
doi:10.1103/PhysRevB.34.5992
[26] H. Baaziz, Z. Charifi, F. El Haj Hassan, S. J. Hashemifar,
and H. Akbarzadeh, “FP-LAPW Investigations of
Zn1–xBexS, Zn1–xBexSe and Zn1–xBexTe Ternary Alloys,”
Physica Status Solidi (B), Vol. 243, No. 6, 2006, pp.
1296-1305.

FP-LMTO Investigation of the Structural and Electronic Properties of CuxAg1–xI Alloys 757
[27] A. Mokhtari and H. Akbarzadeh, “Ab Initio Calculations
of the Electronic and Structural Properties of Beryllium-,
Magnesium- and Calcium-Nitrides,” Physica B, Vol. 337,
2003, pp. 122-129. doi:10.1016/S0921-4526(03)00387-9
[28] A. Bouhemadou, R. Khenata, F. Zegrar, M. Sahnoun, H.
Baltache and A. H. Reshak, “Ab Initio Study of Structural,
Electronic, Elastic and High Pressure Properties of Bar-
ium Chalcogenides,” Computational Materials Science,
Vol. 38, No. 2, 2006, pp. 263-270.
doi:10.1016/j.commatsci.2006.03.001
[29] S. Hull and D. A. Keen, “Pressure-Induced Phase Transi-
tions in AgCl, AgBr, and AgI,” Physical Review B, Vol.
59, No. 2, 1999, pp. 750-761.
doi:10.1103/PhysRevB.59.750
[30] S. Hull and D.A. Keen, “High-Pressure Polymorphism of
the Copper(I) Halides: A Neutron-Diffraction Study to ∼
10 GPa,” Physical Review B, Vol. 50, No. 9, 1994, pp.
5868-5885. doi:10.1103/PhysRevB.50.5868
[31] L.A. Palomino-Rojas, M. Lo´pez-Fuentes, G. H. Co-
coletzi, G. Murrieta, R. de Coss and N. Takeuchi, “Den-
sity Functional Study of the Structural Properties of Sil-
ver Halides: LDA vs GGA Calculations,” Solid State Sci-
ences, Vol. 10, No. 9, pp. 1228-1235.
doi:10.1016/j.solidstatesciences.2007.11.022
[32] T. Söhnel, H. Hermann and P. Schwerdtfeger, “Solid
State Density Functional Calculations for the Group 11
Monohalides,” Journal of Physical Chemistry B, Vol. 109,
No. 1, 2005, pp. 526-531.
[33] T. Ida, M. Mizuno, K. Endo, M. Suhara, K. Nishidate and
K. Nishikawa, “Dynamical Structure of Alpha-Ag_{0.99}
Cu_{0.01}I Crystal by ^{63}Cu NMR Chemical Shift,
Spin-Lattice Relaxation Time and Molecular Dyanmics
Simulation,” Journal of Physics and Chemistry of Solids,
Vol. 63, 2002, pp. 249-256.
doi:10.1016/S0022-3697(01)00137-8
[34] B. Amrani, T. Benmessabih, M. Tahiri, I. Chiboub, S.
Hiadsi and F. Hamdache, “First Principles Study of
Structural, Elastic, Electronic and Optical Properties of
CuCl, CuBr and CuI Compounds under Hydrostatic
Pressure,” Physica B, Vol. 381, 2006, pp. 179-186.
doi:10.1016/j.physb.2006.01.447
[35] F. El Haj Hassan, A. Zaoui and W. Sekkal, “Structural
Properties of Copper Halides,” Materials Science and
Engineering: B, Vol. 87, 2001, pp. 40-47.
doi:10.1016/S0921-5107(01)00687-0
[36] R. C. Hanson, T. A. Fjeldly and H. D. Hochheimer, “Ra-
man Scattering from Five Phases of Silver Iodide,” Phy-
sica Status Solidi (A), Vol. 70, No. 2, 1975, pp. 567-576.
doi:10.1002/pssb.2220700216
[37] M. Hofmann, S. Hull and D. A. Keen, “High-Pressure
Phase of Copper(I) Iodide,” Physical Review B, Vol. 51,
No. 17, 1995, pp. 12022-12025.
doi:10.1103/PhysRevB.51.12022
[38] G. S. Nunes, P. B. Allen and J. L. Martin, “Pressure In-
duced Phase Transitions in Silver Halides,” Physical Re-
view B, Vol. 57, No. 9, 1998, pp. 5098-5105.
doi:10.1103/PhysRevB.57.5098
[39] W. Sekkal, A. Zaoui, A. Laref, M. Certier and H. Aourag,
“Molecular Dynamics Simulation of CuI using a Three-
Body Potential,” Journal of Physics: Condensed Matter,
Vol. 12, No. 28, 2000, p. 6173.
doi:10.1088/0953-8984/12/28/313
[40] R. H. Victora, “Calculated Electronic Structure of Silver
Halide Crystals,” Physical Review B , Vol. 56, No. 8, 1997,
pp. 4417-4421.
[41] V. P. Krüger and J. Pollmann, “Ab Initio Electronic
Structure of Silver Halides Calculated with Self-Interac-
tion and Relaxation-Corrected Pseudopotentials,” Physi-
cal Review B, Vol. 58, No. 7, 1998, pp. 3865-3869.
doi:10.1103/PhysRevB.58.3865
[42] M. Ferhat, A. Zaoui, M. Certier, J. P. Dufour and B. Khe-
lifa, “Electronic Structure of the Copper Halides CuCl,
CuBr and Cul,” Materials Science and Engineering, Vol.
39, 1996, pp. 95-100. doi:10.1016/0921-5107(95)01518-3
[43] O. Zakharov, A. Rubio, X. Blase, M. L. Cohen and S. G.
Louie, “Quasiparticle Band Structures of Six II-VI Com-
pounds: ZnS, ZnSe, ZnTe, CdS, CdSe, and CdTe,” Phys-
ical Review B, Vol. 50, No. 15, 1994, pp. 10780-10787.
doi:10.1103/PhysRevB.50.10780