Materials Sciences and Applicatio n, 2011, 2, 716-720
doi:10.4236/msa.2011.27099 Published Online July 2011 (http://www.SciRP.org/journal/msa)
Electrical Transport Properties of La-BaTiO3
A. I. Ali1,2, Saleh H. Kaytbay3
1Department of Basic Science, Faculty of Industrial Engineering, Helwan University, Cairo, Egypt; 2Department of Physics, Helwan
University, Cairo, Egypt; 3Department of Production, Faculty of Industrial Engineering, Helwan University, Cairo, Egypt.
Received July 20th, 2010; revised November 13th, 2010; accepted May 24th, 2011.
ABSTRACT
The Electrical properties as a function of temperature were investigated at elevated temperatures (300 K - 800 K) on
quenched samples of donor doped La-BaTiO3 system. The resistivity and carrier concentration increased with increas-
ing temperature. Th e mobility of the sa mple shows exponential temperature depe ndence and the value of mobility is in
well agreement with th e theoretical values. From the condu ctivity data the activation energy was calculated (0.036 eV)
and revealed that the conduction mechanism in this system is thermally activated.
Keywords: Hall Mobility, Electrical Resistivity, Microstructure and Dono r Doped-BaTiO3
1. Introduction
The BaTiO3 system has attracted a great deal of attention
due to its excellent dielectric properties, such as low di-
electric loss and low temperature coefficients of dielec-
tric constants. Most importantly is its potential techno-
logical application owing to its unique ferroelectric tran-
sitions. To understand the underlying physics, the elec-
tronic transportation properties of BaTiO3 were exten-
sively investigated by several researchers [1-4]. The total
electrical conductivity of BaTiO3, has been extensively
documented against temperature and oxygen partial
pressure, and the working model of its defect structure is
available [5,6]. The chemical diffusivity is reported [7-11]
as a measure of (oxygen) nonstoichiometry re-equili-
bration kinetics for “undoped” and 1.8 m/o A1-doped
BaTiO3, respectively. Subsequently, thermoelectricity of
mixed ionic electronic conductor BaTiO3 + δ is thermo-
dynamically analyzed and measured across the mixed n/p
regime of both undoped and 1.8 m/o A1-doped BaTiO3
at elevated temperatures [12]. Later on, the electronic
carrier mobilities of BaTiO3 are reported [13]. The mo-
bilities of electrons and holes over the temperature range
800˚C - 1100˚C were determined by measuring electrical
conductivity and chemical diffusivity on undoped and
1.8 m/o Al-doped BaTiO3, respectively, in their mixed
n/p regimes. Later on, the factors that affect the shift of
Curie temperature and the calculated evolution of overall
polarization and dielectric constant of a BaTiO3 crystal
were examined [14]. Many of these reports focused on
the carrier’s mobility, studied at low temperatures. How-
ever, the Hall mobility has received far less attention
partially due to the difficulty of Hall experiment itself, as
well as the low signal of Hall voltage emitted by the Ba-
TiO3 ceramic[15,16]. Recently there is considerable in-
terest in the formation and characterization of the mag-
nitude of the Hall mobility of the electrons in reduced
BaTiO3 single crystal and polycrystalline by Kolodi-
azhnyi [17]. The value of electron density is different
from the expected value. They calculated the mobility
from the relation;
 
T
TN

 
Aassuming
 constant electron density given by the
electro neutrality condition. Unfortunately, all the meas-
urements are only taken in the low temperature range of
the frozen-in oxygen vacancy concentration; no direct
determination of the mobility in the high temperature
range has been reported yet, to my knowledge. For that
reason, defect chemical constant like reduction enthalpy.
In this work, we made La-BaTiO
3 in single phase, we
characterized the samples by using XRD and SEM. We
focused on the electronic transport behavior of lanthanum
doped barium titanate ceramics, paying special attention
to electrical resistivity and Hall mobility at a high tem-
perature range (300 K - 800 K). Also, we found that the
mobility of the reduced sample shows linear temperature
dependence. In what follows, we discuss the conduction
mechanism of the system, the Hall mobility as well as
crystal growth using the theory of semiconductor physics.
In situ high-temperature electrical conductivity and Hall

Electrical Transport Properties of La-BaTiO717
3
measurements have proven useful tools for establishing
doner-doping efficacy in perovskite doped BaTiO3 and to
screen it for potential technological applications.
2. Experimental Work
La- doped BaTiO3 (Ba(1–x)LaxTi(1–x/4)O3; x = 1.0 mol%, x
= 0.01) samples were prepared by a conventional powder
processing unit. The powders (all from Aldrech, U.S.A.)
of BaTiO3 (99.99% pure), TiO2 (99.99%), BaCO3
(99.9%), and La2O3 (99.99%), were intimately mixed in
an ethanol medium with zirconia’s balls by stirring it in a
high-speed turbine at 6000 r.p.m. for 24 hours. The slur-
ring was dried at 100˚C. Mixtures were crushed into
powders and ground lightly in an agate mortar, and then
sieved through a 100 micrometer mesh screen. The
powder was fired at 1200˚C for 5 hours. We repeated this
process and then the powder was molded into a pellet (ca.
2.5 cm length, 1.4 cm width and 2 mm thickness) under a
uni-axial pressure of 15 MPa. This was followed by cold-
isostatically pressing under 150 MPa for 10 min. We
drilled 4 holes in the plate to connect the platinum elec-
trodes. Sintering at 1350˚C for 5 hours followed. Then
we quenched the sample to keep same structure. The
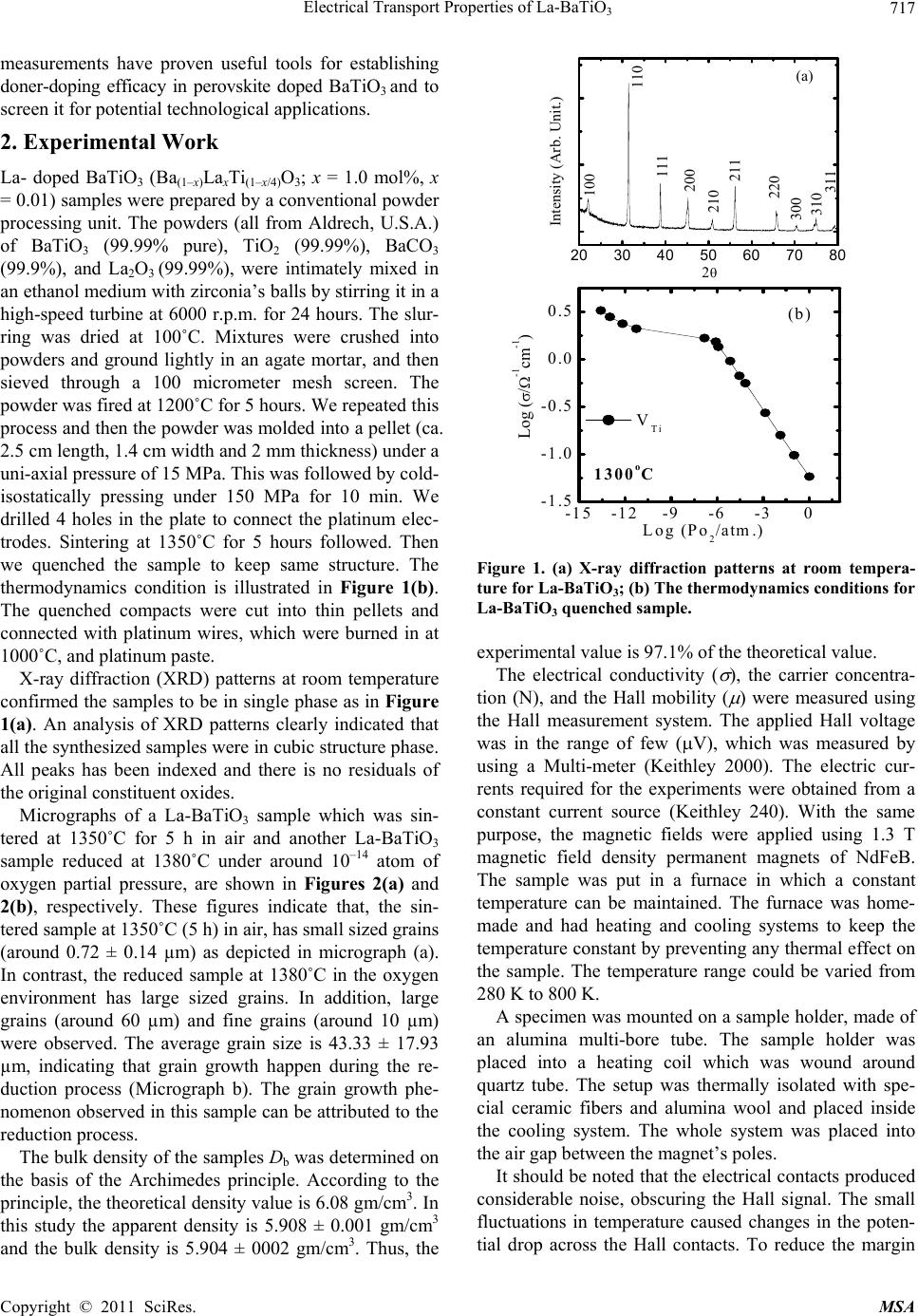
thermodynamics condition is illustrated in Figure 1(b).
The quenched compacts were cut into thin pellets and
connected with platinum wires, which were burned in at
1000˚C, and platinum paste.
X-ray diffraction (XRD) patterns at room temperature
confirmed the samples to be in single phase as in Figure
1(a). An analysis of XRD patterns clearly indicated that
all the synthesized samples were in cubic structure phase.
All peaks has been indexed and there is no residuals of
the original constituent oxides.
Micrographs of a La-BaTiO3 sample which was sin-
tered at 1350˚C for 5 h in air and another La-BaTiO3
sample reduced at 1380˚C under around 10–14 atom of
oxygen partial pressure, are shown in Figures 2(a) and
2(b), respectively. These figures indicate that, the sin-
tered sample at 1350˚C (5 h) in air, has small sized grains
(around 0.72 ± 0.14 µm) as depicted in micrograph (a).
In contrast, the reduced sample at 1380˚C in the oxygen
environment has large sized grains. In addition, large
grains (around 60 µm) and fine grains (around 10 µm)
were observed. The average grain size is 43.33 ± 17.93
µm, indicating that grain growth happen during the re-
duction process (Micrograph b). The grain growth phe-
nomenon observed in this sample can be attributed to the
reduction process.
The bulk density of the samples Db was determined on
the basis of the Archimedes principle. According to the
principle, the theoretical density value is 6.08 gm/cm3. In
this study the apparent density is 5.908 ± 0.001 gm/cm3
and the bulk density is 5.904 ± 0002 gm/cm3. Thus, the
20 30 40 5060 70 80
(a)
311
100
210
211
310
300
220
200
111
2
Intensity (Arb. Unit.)
110
-15 -12-9-6-30
-1.5
-1.0
-0.5
0.0
0.5 (b)
VTi
1300oC
Log (/-1cm-1)
Log (Po2/atm.)
Figure 1. (a) X-ray diffraction patterns at room tempera-
ture for La-BaTiO3; (b) The thermodynamics conditions for
La-BaTiO3 quenched sample.
experimental value is 97.1% of the theoretical value.
The electrical conductivity (  ), the carrier concentra-
tion (N), and the Hall mobility (  ) were measured using
the Hall measurement system. The applied Hall voltage
was in the range of few (V), which was measured by
using a Multi-meter (Keithley 2000). The electric cur-
rents required for the experiments were obtained from a
constant current source (Keithley 240). With the same
purpose, the magnetic fields were applied using 1.3 T
magnetic field density permanent magnets of NdFeB.
The sample was put in a furnace in which a constant
temperature can be maintained. The furnace was home-
made and had heating and cooling systems to keep the
temperature constant by preventing any thermal effect on
the sample. The temperature range could be varied from
280 K to 800 K.
A specimen was mounted on a sample holder, made of
an alumina multi-bore tube. The sample holder was
placed into a heating coil which was wound around
quartz tube. The setup was thermally isolated with spe-
cial ceramic fibers and alumina wool and placed inside
the cooling system. The whole system was placed into
the air gap between the magnet’s poles.
It should be noted that the electrical contacts produced
considerable noise, obscuring the Hall signal. The small
fluctuations in temperature caused changes in the poten-
tial drop across the Hall contacts. To reduce the margin

Electrical Transport Properties of La-BaTiO 718 3
(a)
(b)
Figure 2 (a). SEM microstructure of La-BaTiO3 sample
sintered in Air at 1350˚C; (b). SEM microstructure of La-
BaTiO3 sample sintered at 1350˚C in Air and then
quenched after reducing at 1380˚C and around 10–14 atom
Oxygen partial pressure.
of error, we took every precaution to create stability in
temperature and we repeated the experiment several
times to confirm the results.
3. Results and Discussion
The electrical resistivity of the quenched La-BaTiO3 was
measured and drowns in Figures 3(a). The resistivity is
strongly depended on the degree of previous reduction,
before the measurements of electrical resistivity, the sam-
ple was heated in atmosphere which possessed a well-
defined partial oxygen pressure (as in Figure 1(a)) and
this sample cooled rapidly to room temperature. The re-
sults proved that the resistivity of the La-doped shows
saturation depending on the reduction degree. Also, the
measurements of resistivity below 800 K revealed that,
the curves were completely reversible. And no measur-
able change of composition appeared during the meas-
urements. The resistivity of the reduced sample gradually
decreases with temperature and there is no any discon-
tinuous change in resistivity observed at the temperature
of the phase transition.
Figure 3(b) shows the plots of the dc electrical con-
ductivity as (log dc

) versus temperature as (103/T) over
the temperature range from room temperature to about
800 K. The conductivity behavior for all samples was
similar; it rose linearly with increasing temperature. In-
dicating that the conduction due to thermal activation.
The activation energy for the conduction process was
calculated from the slope of line according to Arrhenius
relation;
0exp g
E
K
T





where 0

is a pre-exponential constant, T is the abso-
lute temperature, K is the Boltzmann’s constant (which
have a unit of electron volt per degree) and Eg is the ac-
tivation energy for electric conduction. The activation
energy for the conduction process is equal 0.036 eV. Eg~
0.048 eV.
Figure 4 (a) shows the plots the carriers concentration
versus temperature as (103/T) over the temperature range
from room temperature to about 800 K. It seems that, the
carriers are nearly temperature independent. The sample
was quenched under reducing conditions from different
300 400 500 600 700 800
0.1
0.2
0.3
0.4
(a)
Temperature (K)
Resisitivity (

.cm)
Resisitivity (Ω·cm)
1.5 2.0 2.5 3.0 3.5
0.00
0.35
0.70
1.05
1.40
(b)
Log  (.cm-1 )
1000/T (K-1)
Log σ (Ω–1·cm–1)
Figure 3. (a) the resistivity as a function of temperature (K)
and (b) the logarithms of conductivity (log () against
1000/T (K–1) for the quenched sample of La-BaTiO3.

Electrical Transport Properties of La-BaTiO719
3
300 400 500 600 700 800
10
18
10
19
10
20
(a)
Carrier Concentration (cm
-3
)
Temperature (K)
300 400500 600700 800
0.0
0.4
0.8
1.2
1.6
(b)
Hall Coefficient (cm
3
/coul)
Temperature (K)
Figure 4. (a) The carriers concentration against temperature
(K); (b) the Hall Coefficient as a function of temperature (K).
temperatures and/or oxygen partial pressures (as in Fig-
ure1 (b)) lead to a well-defined frozen-in oxygen va-
cancy concentration. Assuming a constant electron den-
sity given by the elctroneutrality condition N = [La]3+.
In our work, the experimental carrier concentration (1
- 7) × 1020/cm3 is different from analytical value (1 - 7) ×
1021/cm3, this may be due to the quenching condition. All
samples measured had carrier concentrations between
from1017 to 1020 cm–3/coul. Hall voltages were relatively
small. Typical data is shown in Figure 4(b), the accuracy
of the Hall coefficient measurements on these samples is
no better 10%.
As in Figure 5, the mobility is decreasing with the
temperature in the low temperature range (300 K - 400
K). One can confirm that, as the temperature increases
the mobility nearly constant from around 400 K to 800 K.
It can be concluded that the mobility is essentially inde-
pendent of carrier concentration and that the Hall coeffi-
cient is constant within experimental error over the tem-
perature range from 400 K - 800 K. This is due to the
donors in BaTiO3 are fully ionized over the studied range
of temperature. The sintering and also quenching condi-
tion for the samples as in Figure 1(b) made the carrier
concentration constant with the high temperature phase.
4. Conclusions
Single phase of samples made with out any impurity. The
electrical resistivity decreased with increasing tempera-
300400500 600 700800
0
1
2
3
4
5
Temperature (K)
Mobility

(cm
2
/V.s )
Mobility μ (cm2/V·s)
Figure 5. The Hall mobility as function of temperature (K)
for quenched sample La-BaTiO3.
the activation energy was calculated. The conduction
mechanism of La-BaTiO3 is thermally activated. The
mobility of the system increased with increasing the
temperature indicating that the increase of the charge
carrier’s token place. The carrier’s concentration was
calculated with increasing of the temperature and the
value of the mobility is in agreement with the previous
finding. The all data proven that the doner-doped BaTiO3
is stable at high temperature range of measurements.
Moreover the carriers concentration is quit constant
which make these samples useful for technological ap-
plications
5. Acknowledgements
The author (A. I. Ali) gratefully thanks the financial sup-
port from the Seoul National University, SNU through
the project BK21.
REFERENCES
[1] B. D. Cullity, “Element of X-ray Diffraction,” Addison-
Wesley, London, 1959, p. 329.
[2] C. N. Berglund and W. S. Baer, “Electron Transport in
Single-Domain, Ferroelectric Barium Titanate,” Physical
Review, Vol. 157, No. 2, 1966, pp. 358-366.
doi:org/10.1103/PhysRev.157.358
[3] E. K. Chang, A. Metha and D. M. Smyth, “Electro-
Chemical Society,” In: H. L. Tuller and D. M. Smyth,
Eds., Proceedings of the. Symposium on Electro-Cera-
mics and Solid State Ionics, Princeton, 1988, p. 35.
[4] ASTM, “International Standard Technology Measure-
ments,” V10.50, Designation F76, Annual Book of ASTM
Standards, 1999.
[5] J. Nowotny and M. Rekas, “Defect Structure, Electrical
Properties and Transport in Barium Titanate VII. Chemi-
cal diffusion in Nb-doped BaTiO3,” Ceramics Interna-
tional, Vol. 49, 1991, pp. 135-154.
[6] J. Y. Kim, C. R. Song and H. I. Yoo, “Nonohmic Proper-
ties of Zinc Oxide Ceramics,” Journal of Electro Ceram-
ics, Vol. 1, 1997, p. 27.
doi:org/10.1023/A:1009994230779

Electrical Transport Properties of La-BaTiO3 720
[7] C. R. Song and H. I. Yoo, “Solid State Ionics: Science
&Technology,” In: B. V. R. Chowdari, et al., Eds., World
Scientific Publishing Co., Singapore, 1998, p. 149.
[8] C. R. Song and H. I. Yoo, “Chemical Diffusivity of Ba-
TiO3−δ: I. Experimental Determination,” Solid State Ion-
ics, Vol. 120, No. 1-4, 1999, pp. 141-153.
doi:org/10.1016/S0167-2738(99)00012-0
[9] C. R. Song and H. I. Yoo, “Chemical Diffusivity of Ba-
TiO3-δ: Defect Chemical Analysis,” Physical Review B,
Vol. 61, No. 6, 2000, pp. 3975-3982.
doi:org/10.1103/PhysRevB.61.3975
[10] C. R. Song and H. I. Yoo, “Chemical Diffusivity of Ba-
TiO3−δ: III. Conductivity–Nonstoichiometry (δ) Correla-
tion in a Mixed n/p Regime,” Solid State Ionics, Vol. 124,
No. 3-4, 1999, pp. 289-299.
doi:org/10.1016/S0167-2738(99)00226-X
[11] C. R. Song and H. I. Yoo, “Chemical Diffusivity of Ba-
TiO3−δ: IV, Acceptor-Doped Case,” Journal of the Ame-
rican Ceramic Society, Vol. 83, No. 4, 2000, pp. 773-779.
doi:org/10.1111/j.1151-2916.2000.tb01273.x
[12] H. I. Yoo and C. R. Song, “Thermoelectricity of Ba-
TiO3+δ,” Journal of Electroceramics, Vol. 6, No. 1, 2001,
pp. 61-74. doi:org/10.1023/A:1011425920963
[13] H. I. Yoo, C. R. Song and D. K. Lee, “Electronic Carrier
Mobility of BaTiO3,” Journal of the European Ceramic
Society, Vol. 24, No. 6, 2004, pp. 1259-1263.
doi:org/10.1016/S0955-2219(03)00504-1
[14] Y. Su and G. J. Weng, “The Shift of Curie Temperature
and Evolution of Ferroelectric Domain in Ferroelectric
Crystals,” Journal Mechanical & Physical Solid, Vol. 53,
No. 9, 2005, pp. 2071-2099.
doi:org/10.1016/j.jmps.2005.03.008
[15] R. Moos and K. Heinz, “Electronic Transport Properties
of Sr1−xLaxTiO3 Ceramics,” Journal of Applied Physics,
Vol. 80, No. 1, 1996, p. 393.
doi:org/10.1063/1.362796
[16] R. Moos and W. Menesklon, “Hall Mobility of Undoped
N-type Conducting Strontium Titanate Single Crystals
between 19 K and 1373 K,” Applied Ph ysics A: Materials
Science & Processing, Vol. 61, No. 4, 1995, pp. 389-395.
doi:org/10.1007/BF01540113
[17] T. Kolodiazhnyi, A. Petric, M. Niewczas, C. Bridges, A.
Safa-Sefat and J. Greedan, “Thermoelectric power, Hall
effect, and Mobility of N-type BaTiO3,” Physical Review
B, Vol. 68, No. 8, 2003, pp. 1-5.
doi:org/10.1103/PhysRevB.68.085205
[18] Z. L. Cheng and B. Bergman, “Processing and Structure
Relationships in Electro Spinning of Ceramic Fiber,” Jour-
nal of American Ceramic Society, Vol. 25, No. 4, 2005, p.
441.
[19] J. S. Forrester, E. H. Kisi and A. J. Studer, “Effect of
Interface Mechanical Properties on Pullout in a SiCO3
Fiber Reinforced Lithium Aluminum,” Journal of Ame-
rican Ceramic Society, Vol. 25, No. 4, 2005.