Energy and Power En gi neering, 2011, 3, 361-365
doi:10.4236/epe.2011.33046 Published Online July 2011 (http://www.SciRP.org/journal/epe)
Study on the Synergetic Mechanism for the Dynamic
Evaluation of Electricity Market Operational Efficiency
Chunjie Li, Li Yan, Huiru Zhao
North China Electric Power University, Beijing, China
Received May 10, 2011; revised May 20, 2011; accepted June 7, 2011
Abstract
In Synergetics, when a complex system evolves from one sate to another, the order parameter plays a domi-
nant role. We can analyze the complex system state by studying the dynamic of order parameter. We deve-
loped a synergetic model of electricity market operation system, and studied the dynamic process of the sys-
tem with empirical example, which revealed the internal mechanism of the system evolution. In order to ve-
rify the accuracy of the synergetic model, fourth-order Runge-Kutta algorithm and grey relevance method
were used. Finally, we found that the reserve rate of generation was the order parameter of the system. Then
we can use the principle of Synergetics to evaluate the efficiency of electricity market operation.
Keywords: Electricity Market Operation, Synergetics, Synergetic Model, Order Parameter, Runge-Kutta
Algorithm, Grey Relevance Method
1. Introduction
The electricity market operation, involving the technical
and economic relations b etween generating, tran smitting,
distributing and retailing parts which must be balance-
able at anytime, is a complex system that is open, non-
linear and dynamic. The efficiency evaluation of elec-
tricity market operation system (EMOS) cannot simply
apply the traditional method of the input-output prin-
ciple, but should be in the point of overall dynamic op-
eration. Based on the synergetic theory, we constructed a
synergetic model and found the order parameter of
EMOS. By studying the change of the order parameter
which reflected the system operation state, the efficiency
evaluation mechanism of electricity market operation
was revealed.
2. Introduction of Synergetics
Synergetics was created by Haken, a German physicist.
It is a self-organized theory studying nonlinear interac-
tion between subsystems which will result in ordered
evolution of the system structure. The key point of Syn-
ergetics is how an open, erratic system evolves from a
disordered structure to an ordered state, or from one or-
dered state to another one.
The general steps dealing with the issues of Synerge-
tics are as following [1,2]:
1) “Translate” the specific issues to mathematical
problems. Explore the relationships between key vari-
ables and constants which these two parameters deter-
mine the system operation state. Then construct mathe-
matical model. The basic evolution equations of Syner-
getics can be written in the form of Langevin equations:


,uKus F



u
 is the change rate of state variables; are state
variables that can be macro or micro; u
s
are control pa-
rameters;
F
is random noise. The evolution model is
differential equation or equations containing and its
derivative. u
2) In order to test the accuracy of the synergetic model,
calculate with computer. Then compare the simulated
results with initial values.
3) Find order parameters in the model by distinguish-
ing the size of damping coefficients.
4) Based on the Synergetic servo principle, cancel fast
variables and get order parameter equations. By analyz-
ing the dynamic of the order parameter, evaluate the state
of the system.
3. Synergetic Features of Electricity Market
Operation
Synergetics is mainly used to study open, non-linear,

C. J. LI ET AL. 362
erratic complex systems. The open feature means that the
system exchanges energy, material and information with
outside. The non-linear feature shows that the nonlinear
mechanism between variables of the system exists. The
essence of unbalance is that the system state is changing
with time [3].
EMOS is an open system that exchanges energy, ma-
terial and information with natural and social environ-
ment. For example, coal-fired power plants need to pur-
chase coal in the energy market. The construction in-
vestment of the plants is affected by national economic
development and macroeconomic policy, etc.
Although there are complex technical and economic
relations between the generating, transmitting, distribut-
ing and retailing subsystems, they must be coordinate
highly, e.g. the variables of EMOS varied with time, but
they are generally in coordination and non-linear condi-
tions.
EMOS is in erratic state. For reasons above, in the
process of electricity market operation, the system ex-
changes material and information with outside, and pro-
vides power to users by tracking load at any time. In
other word, the system is always in dynamic equilibrium
state [4].
For all above, EMOS has synergetic evolution features
of complex system and accords with the principles of
Synergetics.
4. Synergetic Model of E lectricit y Market
Operation
4.1. Select State Variables
To create the synergetic model of EMOS, we should
select the state variables first.
Based on the SCP principle of Harvard School, the
electricity market is divided into three parts: market
structure, market conduct and market performance. In
SCP, structure determines conduct, further more, conduct
determines performance. But it’s not a simple one-way
relationship. At the same time, conduct can affect struc-
ture, and performance can react on structure and conduct
either [5-7]. For above, we divide the EMOS into three
subsystems: structure subsystem, conduct subsystem and
performance subsystem. Four state variables are selected:
declared supply and demand ratio (SDR), reserve rate of
generation (RG), transacted power amount (TP) and
market clearing price (CP). These state variables are de-
scribed in Table 1.
4.2. Synergetic Model
Let

1
X
t,

2
X
t,

3
X
t,

4
X
t represent SDR, RG,
Table 1. Description of the state variables of electricity
market operation.
State
variables Implication
SDR The formula is: de cl ared supply/declared demand.
RG The formula is: (available generation amount-actual
power demand)/available generation amount
TP The actual transacted power amount after bidding.
CP The market clearing price after bidding.
TP and CP individually. Based on Synergetics, we sup-
pose that the change rate of

i
X
t is


dd
i
X
tt
which is determined by following: the first factor is the
inside synergy effect of the state variables. That is the
development and inhibition effect of the state variable
itself. The other factor is the outside synergy effect of the
state variables. That is the cooperation and competition
effect from the other state variables. The inside synergy
items of the ith state variable are and

ii i
aX t


2
ii i
bXt .
The outside synergy items are and

ij j
aX t


2
ij j
bXt .
We cannot tell which ones are development and coopera-
tion items, and which are inhibition and competition ones.
So it is assumed that the coefficients of all items are
positive. The exact symbol will be given by the model
results.
Based on the discussion above, the synergetic model
of EMOS is:

 
 


2
42
1,
d
d
i
j
iii iii
ij jiji
jji
Xt aX tbXt
t
aXtbXtf t




(1)
In model (1),


i
f
t is the outside interference that is
influenced by environment and policy. The main purpose
of this paper is to find the order parameter of EMOS by
studying the interaction of state variables, but not to
forecast when the electricity market develops from an
ordered state to another by the help of outside interfer-
ence. So we suppose


0ft
i

in this paper.
4.3. Find the Order Parameters
In Synergetics, when system tends to the critical po int, it
evolves from a disordered structure to an ordered state,
or from one ordered state to another one. At this point,
the state variables will develop into two categories:
variables changing rapidly with time are known as the
fast variables; the other kinds change very slowly, known
as the slow variables which are the order parameters. The
order parameter, a core concept of Synergetics, can lead
to new structure of the system, and reflect the ordered

C. J. LI ET AL. 363
degree of the new structure [8-11]. Haken established
two synergetic research methods: micro and macro
method. From the point of micro method, we can find the
order parameters through the size of damping co-
efficients in synergetic model. And from the point of
macro method, the principle of maximum information
entropy is used to find the order parameters. But some
problems exit in macro method: it is not sure that the
information entropy increases or deceases when the sys-
tem is developing from one state to another. So we use
the micro method to find order parameter in this paper.
above into the synergetic model (1), and get the equa-
tions with the help of MATLAB: (see (2))
This is the synergetic model of the regional electricity
market.
5.2. Verifying the Model
In model (2), in order to simplify the calculation, the first
and second power of the items were considered, the
higher power items were omitted. So the accuracy of the
synergetic model needs to be verified, we use fourth-
order Runge-Kutta method and grey relevance method to
verify the model.
5. Case Study
5.1. The Synergetic Model of a Regional
Electricity Market 5.2.1. Verifying by Fourth-Order Runge - Kutta Algorithm
Using fourth-order Runge-Kutta algorithm, we got the
numerical solution of model (2). Comparing the simu-
lated data


1
i
X
t
 with initial data


1
i
X
t, we made
the trend figures of these data. See Figure 1 and Figure
2.
Based on the synergetic model of EMOS above, we will
analyze a regional electricity market in this part. Table 2
is the operation data of the market in year 2008 and
2009.
Since the unit and magnitude of the initial data is dif-
ferent, we normalize the data first:

  
 

0min
max min
1,2,,4; 1,2,24.
ii
t
iii
t t

X
tXt
Xt
X
tX
it



We can see the trends of initial data and simulated
data are identical approximately. So model (2) is rea-
sonable.
t
5.2.2. Verifyin g b y Grey Rel e va nce Met ho d
The fit degree of the model has b een displayed intu itively
above. To verify the model further, we calculate the grey
relevance degree of the initial and simulated data series
[12,13]. The result is in Table 3.
In order to weaken the randomness of the time series,
we cumulate the normalized data, and get new series


1
i
X
t: Based on the grey relevance theory, the relevance co-
efficient is 0.5 generally. If the grey relevance degree is
more than 0.6, we can consider the model is satisfied.
From Table 3, the results are all more than 0.6. So model
(2) is good.



 
10
1
, 1,2,24.
k
ii
t
XkXt k



Using least square method, we substitute the data



































12
11 11 111 23
222
111
234
12
11 11 222 13
d0.1971 0.02440.35730.46430.2675
d
0.02520.00960.0158
d0.09060.00160.73490.0141 0.7306
d
0.06
Xt 1
4
1
4
X
tXt XtXtX
t
XtXt Xt
Xt
t
X
tXt XtXtX
t
 

 









t



























22
111
2
134
(1) 2
11 11
333 12
222
111
124
(1) 2
11 1
444 1
07() 0.00510.0421
d()0.28180.01510.0237 0.05550.4852
d
0.03330.05820.0281
d()0.3059 0.00990.5345
d
Xt Xt Xt
Xt 1
4
X
tXt XtXtX
t
XtXt Xt
Xt Xt XtXt
t

 

 













11
23
222
111
123
0.0397 0.6089
0.02670.00830.043
t
X
tX
XtXt Xt





















t
(2)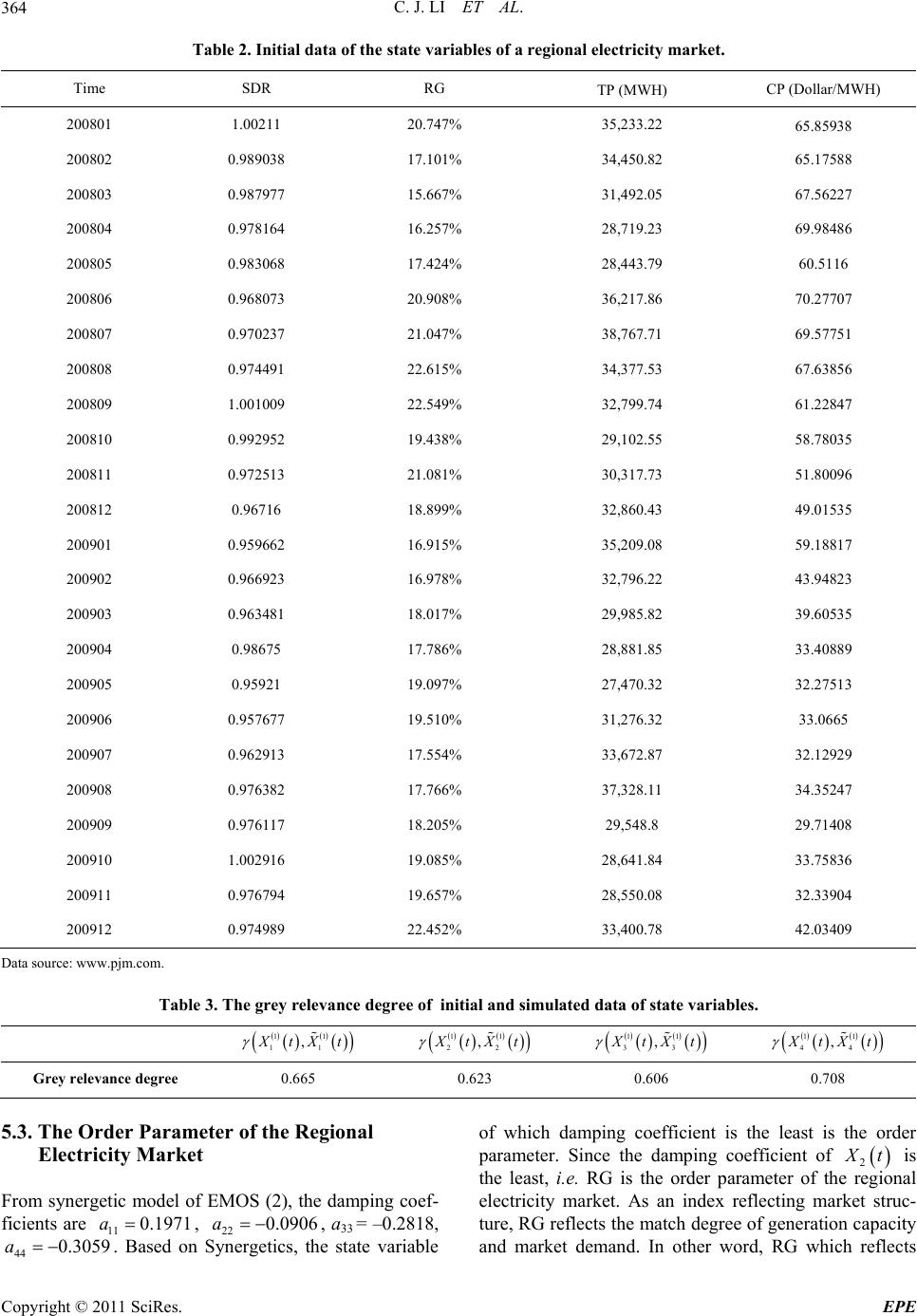

C. J. LI ET AL. 364
Table 2. Initial data of the state variables of a regional electricity market.
Time SDR RG TP (MWH) CP (Dollar/MWH)
200801 1.00211 20.747% 35,233.22 65.85938
200802 0.989038 17.101% 34,450.82 65.17588
200803 0.987977 15.667% 31,492.05 67.56227
200804 0.978164 16.257% 28,719.23 69.98486
200805 0.983068 17.424% 28,443.79 60.5116
200806 0.968073 20.908% 36,217.86 70.27707
200807 0.970237 21.047% 38,767.71 69.57751
200808 0.974491 22.615% 34,377.53 67.63856
200809 1.001009 22.549% 32,799.74 61.22847
200810 0.992952 19.438% 29,102.55 58.78035
200811 0.972513 21.081% 30,317.73 51.80096
200812 0.96716 18.899% 32,860.43 49.01535
200901 0.959662 16.915% 35,209.08 59.18817
200902 0.966923 16.978% 32,796.22 43.94823
200903 0.963481 18.017% 29,985.82 39.60535
200904 0.98675 17.786% 28,881.85 33.40889
200905 0.95921 19.097% 27,470.32 32.27513
200906 0.957677 19.510% 31,276.32 33.0665
200907 0.962913 17.554% 33,672.87 32.12929
200908 0.976382 17.766% 37,328.11 34.35247
200909 0.976117 18.205% 29,548.8 29.71408
200910 1.002916 19.085% 28,641.84 33.75836
200911 0.976794 19.657% 28,550.08 32.33904
200912 0.974989 22.452% 33,400.78 42.03409
Data source: www.pjm.com.
Table 3. The grey relevance degree of initial and simulated data of state variables.





11
11
,XtXt 







11
22
,XtXt 







11
33
,XtXt 






11
44
,XtXt 

Grey relevance degree 0.665 0.623 0.606 0.708
5.3. The Order Parameter of the Regional
Electricity Market
From synergetic model of EMOS (2), the damping coef-
ficients are , 2211 0.1971a0.0906a

, a33 = –0.2818,
. Based on Synergetics, the state variable
of which damping coefficient is the least is the order
parameter. Since the damping coefficient of
44 0.30a 59


2
X
t is
the least, i.e. RG is the order parameter of the regional
electricity market. As an index reflecting market struc-
ture, RG reflects the match degree of generation capacity
and market demand. In other word, RG which reflects

C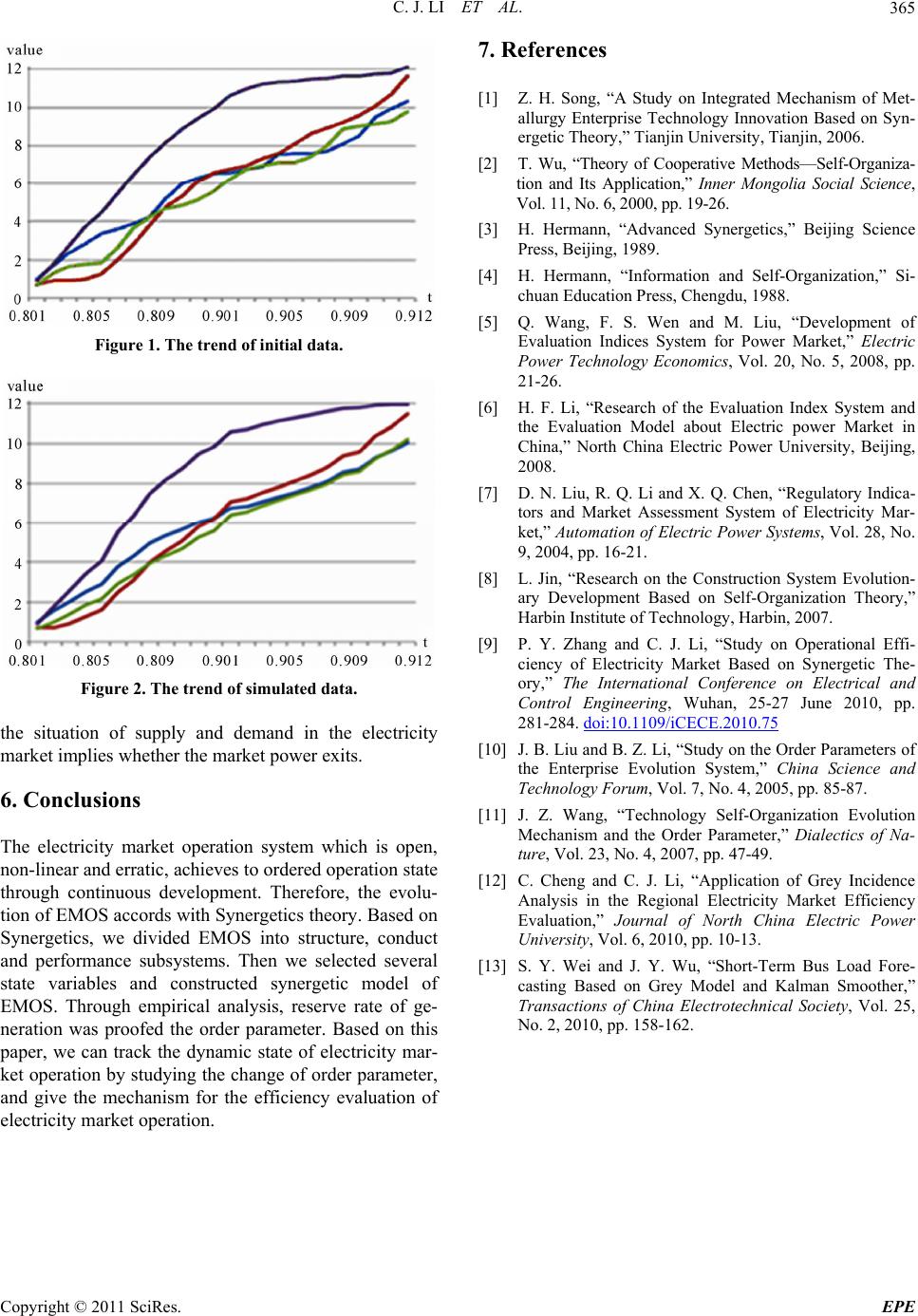. J. LI ET AL.365
Figure 1. The trend of initial data.
Figure 2. The trend of simulated data.
the situation of supply and demand in the electricity
market implies whether the market power exits.
6. Conclusions
The electricity market operation system which is open,
non-linear and erratic, achieves to ordered operation state
through continuous development. Therefore, the evolu-
tion of EMOS accords with Synergetics theory. Based on
Synergetics, we divided EMOS into structure, conduct
and performance subsystems. Then we selected several
state variables and constructed synergetic model of
EMOS. Through empirical analysis, reserve rate of ge-
neration was proofed the order parameter. Based on this
paper, we can track the dynamic state of electricity mar-
ket operation by studying the change of order parameter,
and give the mechanism for the efficiency evaluation of
electricity market operation.
7. References
[1] Z. H. Song, “A Study on Integrated Mechanism of Met-
allurgy Enterprise Technology Innovation Based on Syn-
ergetic Theory,” Tianjin University, Tianjin, 2006.
[2] T. Wu, “Theory of Cooperative Methods—Self-Organiza-
tion and Its Application,” Inner Mongolia Social Science,
Vol. 11, No. 6, 2000, pp. 19-26.
[3] H. Hermann, “Advanced Synergetics,” Beijing Science
Press, Beijing, 1989.
[4] H. Hermann, “Information and Self-Organization,” Si-
chuan Education Press, Chengdu, 1988.
[5] Q. Wang, F. S. Wen and M. Liu, “Development of
Evaluation Indices System for Power Market,” Electric
Power Technology Economics, Vol. 20, No. 5, 2008, pp.
21-26.
[6] H. F. Li, “Research of the Evaluation Index System and
the Evaluation Model about Electric power Market in
China,” North China Electric Power University, Beijing,
2008.
[7] D. N. Liu, R. Q. Li and X. Q. Chen, “Regulatory Indica-
tors and Market Assessment System of Electricity Mar-
ket,” Automation of Electric Power Systems, Vol. 28, No.
9, 2004, pp. 16-21.
[8] L. Jin, “Research on the Construction System Evolution-
ary Development Based on Self-Organization Theory,”
Harbin Institute of Technology, Harbin, 2007.
[9] P. Y. Zhang and C. J. Li, “Study on Operational Effi-
ciency of Electricity Market Based on Synergetic The-
ory,” The International Conference on Electrical and
Control Engineering, Wuhan, 25-27 June 2010, pp.
281-284. doi:10.1109/iCECE.2010.75
[10] J. B. Liu and B. Z. Li, “Study on the Order Parameters of
the Enterprise Evolution System,” China Science and
Technology Forum, Vol. 7, No. 4, 2005, pp. 85-87.
[11] J. Z. Wang, “Technology Self-Organization Evolution
Mechanism and the Order Parameter,” Dialectics of Na-
ture, Vol. 23, No. 4, 2007, pp. 47-49.
[12] C. Cheng and C. J. Li, “Application of Grey Incidence
Analysis in the Regional Electricity Market Efficiency
Evaluati on,” Journal of North China Electric Power
University, Vol. 6, 2010, pp. 10-13.
[13] S. Y. Wei and J. Y. Wu, “Short-Term Bus Load Fore-
casting Based on Grey Model and Kalman Smoother,”
Transactions of China Electrotechnical Society, Vol. 25,
No. 2, 2010, pp. 158-162.