Circuits and Systems
Vol.07 No.08(2016), Article ID:67652,10 pages
10.4236/cs.2016.78165
Fuzzy Empowered Cognitive Spatial Relation Identification and Semantic Action Recognition
R. I. Minu1, G. Nagarajan2
1Department of Computer Science and Engineering, Jerusalem College of Engineering, Chennai, India
2Department of Electrical and Electronic Engineering, Sathyabama University, Chennai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2016; accepted 20 April 2016; published 24 June 2016
ABSTRACT
Automatic labeling of the action held by the players in a live-in sports video is the main motivation of this paper. In this paper, we proposed a fuzzy-based action recognition system from a basketball sports image. This paper deals with the intellectual sports event action recognition from a live video stream. It required an intelligent system which would automatically and semantically label the action in the videos through machine understandability concept. The machine knowledge can be feed through the domain ontology of particular sports event. The major required component for this kind of system is an efficient image analysis component and automation action labelling component. The image is labelled using Type-2 Fuzzy set concept.
Keywords:
SIFT, Type II Fuzzy, Segmentation, JSEG, RCC

1. Introduction
Human action recognition from a live video streaming is one of the emerging and challenging research topics in computer vision. Action recognition from a still image is one of the profound area researches for past years. Recently Ijjina et al. [1] provide an accuracy rate of 99.98% on human action recognition using UCF50 dataset.
In this paper, the bag-of-visual word is created using the significant, low-level feature such as dominant color, scalable color, color layout, edge histogram and SIFT. Using these features, a visual word has been created which can be used as a data attribute in the created fuzzy basketball sports event ontology. To fulfill the objective of this paper, a fuzzy-based concept was implemented to identify the action on the given sports event image. For this concept, fuzzy-based image recognition algorithm was used to label the action held on the given image. For implementation, basketball domain image dataset from Stanford University was used.
This paper is organized in such a way that initially the background details about the recent state-of-art of the human action recognition technique and the overall proposed procedure is briefed. Then the concept of the semantic segmentation and the spatial relation based labeling with the help of fuzzy technology is explained.
2. Background
The recent work on human action recognition is elaborated in this section. Ijjina et al. [1] produce a recognition rate of 99.98% by using UCF50 dataset. The author utilizes deep convolutional neural networks which were initialized by a genetic algorithm. Ben et al. [2] in this paper try to classify the human body action by analyzing the skeletons. They developed tools with smoothing, denoising, temporal registration and extraction of action in a time domain. Johanan et al. [3] compare the Gaussian mixture model based action recognition algorithm with Fisher vectors model with symmetric positive definite matrices and linear subspaces. In their evaluation Fisher vector model obtains higher accuracy rate for scale invariant and ideal condition. In general Khurram & Zamir [4] provided an insight and adopting the action recognition in UCF sports dataset. They had summarized the overall process into three steps local feature extraction, learning, and classification.
With respect to basketball sport, some of the primitive actions are listed in Figure 1. Each action is further classified into several types which are beyond the scope of this paper.
The steps involved in identifying the action are shown in Figure 2. Initially, the images are segmented semantically using the concept of Multi-class image semantic segmentation (MCISS) (Gao et al., [5] ). From the segmented image, the overlapping of the image objects is determined using the cognitive spatial relationship between them. As each action has a different kind of overlaying relationship, a Type-2 trapezoidal membership function was used to label the actual action held on the image.
3. Semantic Image Segmentation
Semantic segmentation is one of the most crucial steps for many applications such as image editing and content-based image retrieval. Existing MCISS [5] approaches often consider only the top-down process and suffer from poor label consistency among neighboring pixels. To overcome this limitation, this work proposes a combined MCISS method to integrate a state-of-the-art top-down (TD) approach Semantic Texton Forests (STF) and a classical bottom-up (BU) approach JSEG to exploit their relative merits. Experimental results on two challenging datasets show that the proposed method can achieve higher accuracy in comparison with the original
Figure 1. Types of basketball action.
Figure 2. Steps involved for action recognition.
Figure 3. Semantic segmentation.
STF method while it does not notably prolong the computational time. However, JSEG has some disadvantages; several limitations are found for the algorithm. One case is when two neighbor regions do not have a clear boundary, then over segmentation problem reduces the segmentation quality. We can improve this by using modified versions of JSEG called fractal JSEG, which is an improved version of the JSEG color image segmentation algorithm, combining the classical JSEG algorithm and a local fractal operator that measures the fractal dimension of each pixel, thus improving the boundary detection in the J-map, which shows improved results in comparison with the classical JSEG algorithm. Another approach called I-FRAC which was specified by Karin el al. [6] also shows better results for some class of images where a variation of colors is too low .hence in this work an approach that uses both algorithms based on selection criteria is implemented. This work is based on the assumption that by improving the segmentation accuracy of bottom approach overall segmentation accuracy can be improved. The implementation analysis of this work is explained in [7] . The overall sketch of image semantic segmentation is shown in Figure 3.
4. Cognitive Spatial Relation Identification
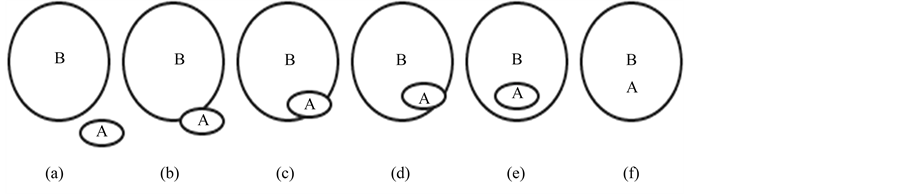
The fundamental problem of computer vision is that of recognizing the objects represented in the image using the prior knowledge of the model in it. The features extracted from the segmented image are represented as the model in this action recognition scenario. The identification of the action is performed by a standard classification procedure, through direct mapping of the feature vector of the trained image set to the test image set. In this work the connectivity between connected regions of the views is described by means of the formalism of region connection calculus (RCC). In RCC, the topological properties of the disconnected regions of the views are encoded into a structure of co-circuits. This set of co-circuits is one of the several combinational structure referred through relative positioning. Actually, only nine of the RCC have a meaningful interpretation in physical space and are referred to as “disjoint”, “meet”, “equal”, “inside”, “covered by”, “contains”, “covers”, and “overlap” (both with disjoint or intersecting boundaries). The utilized six of eight RCC combinations are shown in Figure 4 [Figure 4(a) Disconnected DC(a,b); Figure 4(b) Extremely connected EC(a,b); Figure 4(c) Partially overlapped PO(a,b); Figure 4(d) Tangential proper part TPP(a,b); Figure 4(e) Non-tangential proper part NTPP(a,b); Figure 4(f) Equal EQ(a,b)].
Thus by implementing the region connection calculus strategies, the action held on the given image is identified. For this, initially, the image is semantically segmented as specified. From the segmented image, the notable object such as a ball, hoop, and the human body is identified. For this identification silhouette of this object are compared and identified. From the identified objects outlines the region connection calculus relationships are determined to come up with wise decision making. In short the processes are listed below and shown in Figure 5.
・ The given image is segmented precisely through semantic segmentation,
・ The connected edges of the segmented image are compared with the trained silhouette of ball, hoop, and human to identify the notable object in the given image,
・ Once the object is identified, there RCC combination is determined.
Each action agrees upon all the eight extensive region connection calculus combination. Thus just by identifying the spatial relationship between the ball-hoop, ball-human, and human-hoop it is tough to identify the action. Thus, it required a fuzzy kind of decision-making algorithm to crack the issues. Figure 6 shows the some of the possible object connection calculus for the Dunk action. This figure shows the toughness required to strengthen the system.
In general fuzzy technique was used for image segmentation [8] . The basic idea of fuzzy logic was used to
Figure 4. Eight common RCC.
Figure 5. The spatial connection identification.
Figure 6. The spatial connection identified on dunk action image.
accomplish knowledge information from a vague set of data. If X is a collection of n different xn data sets, then a fuzzy set F with respect to X can be denoted in ordered pair
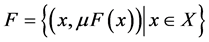 . (1)
. (1)
The membership functions are used to map every element in X to a value in A which ranges from [0, 1] interval. These membership functions are designed with respect to a certain graphical structure like S-function, Z-function, and Triangular, Trapezoidal, Gaussian, PI and Vicinity membership function. With respect to the domain, the function can be selected. In this paper Type-II Trapezoidal membership function was used.
Let consider an action Dunk. From Figure 7, the distance between the ball-human, ball-hoop and ball-hoop are calculated manually by incorporating the segmented ground truth image in a graph.
So for an action Dunk to decide which cognitive spatial relation will suit is decided by the distance between the ball with a hoop, hand, and player. So from Figure 7, the distance between the ball-human is 20 to 60 pixel value.
To provide a precise decision on kind of action and to solve this hypothetical uncertainty fuzzy system was used. For the given image the uncertainty decision as shown in Figure 8 would arise.
As shown in Equation (2), the Type-2 fuzzy set requires two sets of membership function value. Here, X denotes the primary set of data and Zx is called the secondary set of data. The membership function degree of the secondary set of data will be always equal to one which is symbolically explained as {(x, v), 1}. Now, the membership function can be categorized into lower membership function (LMF) and upper membership function (UMF). Thus, the distance similarity can be fixed between the values of 1 to 10. When the value ranges
Figure 7. Dunk action analyses.


Figure 8. (a) Decision with respect to ball (b) Action-cognitive_spatial_relation.
from 1 to 3, the object is said to touch spatially and all the related action in touch relation would come as a query result. Still, in order to refine the result, a range can be specified for each action. The membership function calculation would be as shown in Figure 13.
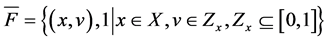 . (2)
. (2)
As shown in Equation (2), the Type-2 fuzzy set requires two sets of membership function value. Here, X denotes the primary set of data and Zx is called the secondary set of data. The membership function degree of secondary set of data 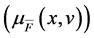 will be always equal to one which is symbolically explained as {(x, v), 1}. Now, the membership function can be categorized into lower membership function (LMF) and upper membership function (UMF). Thus, the distance similarity can be fixed between the values of 1 to 10. When the value ranges from 1 to 3, the object is said to touch spatially and all the related action in touch relation would come as query result. Still, in order to refine the result, a range can be specified for each action. The membership function calculation would be as shown in Figure 9.
will be always equal to one which is symbolically explained as {(x, v), 1}. Now, the membership function can be categorized into lower membership function (LMF) and upper membership function (UMF). Thus, the distance similarity can be fixed between the values of 1 to 10. When the value ranges from 1 to 3, the object is said to touch spatially and all the related action in touch relation would come as query result. Still, in order to refine the result, a range can be specified for each action. The membership function calculation would be as shown in Figure 9.
The fuzzy system is represented in residual lattices with respect to lattice and monoid as L = (L, ≤, ., I). The lattices (variable 1 ≤ variable 2) provide the possible maximum and minimum value for the variable and the monoid (variable 1. variable 2) describes the logical reasoning used in the fuzzy system. In this fuzzy system, the union and intersection are used to find the touch and overlap spatial relationship between the items. So, the representation of this semantic search engine using fuzzy logic would be as shown in Equation (3).
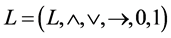 (3)
(3)
The fuzzy values can be formalized in a formal concept analysis way to verify whether the ontology built through fuzziness provides completeness to the ontology. The context of a concept is explained with the triplets (object, attribute, relation). So, for this system, the object would be the spatial relation class values and the attribute is the value calculated from the image. With respect to these values, the action can be determined.
5. Experimental Results
The whole concept of action recognition is implemented as a separate GUI in Matlab to analyze the precision of the procedure to identify the action. Figure 10 shows the implementation framework. For the given input image, say query image the distance between the objects is identified. From the identified values the fuzzy membership function is used to identify the action held on the given image.
As shown in Figure 11, this procedure gives a 100% precision and recall result. Thus, the identified action is used as attribute in the created ontology.
Figure 12 shows the Mean Average Precision (MAP) for different sports event recognition with respect to three different systems. The accuracy of different leading system says Kesorn and Poslad [9] OVSS, Elfiky et al. [10] Pyramid BOW with our approach.
Table 1 shows the possible distance for Dunk action for 4 test cases. The precision and recall factor of using visual word and using fuzzy for action recognition is shown in Table 2.
So as shown in Figure 13, to measure the classification performance quantitatively a Precision-Recall curve is computed and its average Precision-Recall is found from the graph. Precision is the fraction of the images classified to respective action that are relevant to the user’s query image. The recall is the fraction of the images classified, that are relevant to the queries that are successfully classified. From the Precision-Recall plot, the area
Figure 9. Membership functions calculation for dunk action.
Figure 10. Implementation of action recognition using fuzzy type II.
Figure 11. Precision-recall and ROC curve of the given input.
Table 1. Range of values for dunk action.
Table 2. Image recognition rate.
Figure 12. MAP for image recognition.
Figure 13. Precision-recall-average precision-recall for image recognition.
under the precision-recall curve gives the Average Precision Recall. The AP provides an accuracy of 83.5% for the given Basketball event image.
5. Conclusion
In this paper, the procedure for identifying the action on given sports image was briefly explained. To identify the action, initially the image is segmented using a unique semantic segmentation procedure. From the segmented images, the objects on them with respect to the selected sports domain, such as ball, human and hoop are identified using the predefined silhouette of the objects. From the identified object, the distance between them where calculated. From the determined values, a Type-2 based membership function is used to label the action on image. For experimental analysis, we used basket ball game which provides an precision of 100%. When analyzing with respect to specific action there is a recognition rate of 83.5%. This can be improvised by utilizing intelligent feature extraction algorithm.
Cite this paper
R. I. Minu,G. Nagarajan, (2016) Fuzzy Empowered Cognitive Spatial Relation Identification and Semantic Action Recognition. Circuits and Systems,07,1906-1915. doi: 10.4236/cs.2016.78165
References
- 1. Ijjina, E.P. and Chalavadi, K.M. (2016) Human Action Recognition Using Genetic Algorithms and Convolutional Neural Networks. Pattern Recognition, in Press.
http://dx.doi.org/10.1016/j.patcog.2016.01.012 - 2. Amor, B.B., Su, J.Y. and Srivastava, A. (2016) Action Recognition Using Rate-Invariant Analysis of Skeletal Shape Trajectories. IEEE Transactions on Pattern Analysis and Machine Intelligence, 38, 1-13.
http://dx.doi.org/10.1109/TPAMI.2015.2439257 - 3. Carvajal, J., et al. (2016) Comparative Evaluation of Action Recognition Methods via Riemannian Manifolds, Fisher Vectors and GMMs: Ideal and Challenging Conditions.
http://arxiv.org/pdf/1602.01599v1.pdf - 4. Soomro, K. and Zamir, A.R. (2014) Action Recognition in Realistic Sports Videos. In: Moeslund, T.B., Thomas, G. and Hilton, A., Eds., Computer Vision in Sports, Springer International Publishing, Switzerland, 181-208.
http://dx.doi.org/10.1007/978-3-319-09396-3_9 - 5. Gao, C., Zhang, X. and Wang, H. (2012) A Combined Method for Multi-Class Image Semantic Segmentation. IEEE Transactions on Consumer Electronics, 58, 596-604.
http://dx.doi.org/10.1109/TCE.2012.6227465 - 6. Komati, K.S., Salles, E.O.T. and Filho, M.S. (2009) Fractal-JSEG: JSEG Using an Homogeneity Measurement Based on Local Fractal Descriptor. 2009 XXII Brazilian Symposium on Computer Graphics and Image Processing, Rio de Janiero, 11-15 October 2009, 253-260.
- 7. Madhu, K. and Minu, R.I. (2013) Image Segmentation Using Improved JSEG. 2013 International Conference on Pattern Recognition, Informatics and Mobile Engineering (PRIME), Salem, 21-22 February 2013, 37-42.
http://dx.doi.org/10.1109/icprime.2013.6496444 - 8. Gómez, D., Yáñez, J., Guada, C., Rodríguez, J.T., Montero, J. and Zarrazola, E. (2015) Fuzzy Image Segmentation Based upon Hierarchical Clustering. Knowledge-Based Systems, 87, 26-37.
http://dx.doi.org/10.1016/j.knosys.2015.07.017 - 9. Kesorn, K. and Poslad, S. (2012) An Enhanced Bag-of-Visual Word Vector Space Model to Represent Visual Content in Athletics Images. IEEE Transactions on Multimedia, 14, 211-222.
http://dx.doi.org/10.1109/TMM.2011.2170665 - 10. Elfiky, N.M., et al. (2012) Discriminative Compact Pyramids for Object and Scene Recognition. Pattern Recognition, 45, 1627-1636.
http://dx.doi.org/10.1016/j.patcog.2011.09.020