Open Journal of Social Sciences
Vol.04 No.03(2016), Article ID:64548,6 pages
10.4236/jss.2016.43011
Dynamic Option Pricing Model Based on the Realized-GARCH-NIG Approach
Honglei Zhang1, Yixiang Tian1, Gaoxun Zhang2
1School of Management and Economics of UESTC, Chengdu, 611731, China
2School of Science, Southwest University of Science and Technology, Mianyang, 621010, China



Received 8 March 2016; accepted 12 March 2016; published 15 March 2016
ABSTRACT
In this paper, we take the advantage of high frequency data to develop option pricing model and select the Realized GARCH model to describe the volatility of assets, use NIG distribution to describe the distribution of underlying assets, and also build the Realized-GARCH-NIG model to price the option. Finally, we obtain the dynamic option pricing model based on the Realized-GARCH-NIG approach. To verify the effect of the dynamic option pricing model based on the Realized-GARCH- NIG approach, this paper provides the empirical analysis between the dynamic option pricing model based on the Realized-GARCH-NIG approach and the B-S option pricing model. The results show that the option value obtained from the dynamic option pricing model based on the Realized-GARCH-NIG approach is more accurate and effective than the B-S option pricing model.
Keywords:
Option Pricing Model, Realized GARCH Model, High Frequency Data, NIG Distribution

1. Introduction
Option is a derivative financial tool, which now has become an important risk management tool for investors. The estimation and forecast of asset volatility have a great influence on option value, which have become the important direction of current option pricing research. Black and Scholes [1] derived the B-S option pricing model with risk neutral conditions, which lay a solid foundation for modern option pricing theory. Merton and Robert [2] considered the jump process in the market price volatility, and proposed the option pricing model based on market price jump-diffusion process. Hull, John, and Alan White [3] built random price volatility model by modeling the volatility with random process method, and proposed the option pricing model with random volatility diffusion. Duan [4] built an option pricing model by estimating the time-varying characteristics of asset volatility with GARCH model. Melick, William and Thomas [5] considered the mixed distribution assumption in the price dynamics process, presented the option pricing model that assets return follows the mixed normal distribution, and conducted empirical analysis to obtain better results. Duan [6] considered the characteristics of fat tail, sharp peak and skewness distribution, and built option pricing model based on GARCH-GED. But GED distribution selected by Duan is still symmetric, which can’t describe the asymmetric distribution characteristics of assets. Chorro [7] selected more general generalized hyperbolic distribution to describe the distribution characteristics of assets, described the dynamic process of asset price with GARCH process, built option pricing model based on GARCH-GH, and improved the accuracy of option pricing model by conducting empirical analysis on CAC40 and SP500 index options.
Efficient estimation on asset volatility and distribution characteristics is an important factor affecting the option pricing model. As high frequency data is widely used in recent years, many econometricians start to take the advantages of high frequency data into account, and directly model the volatility of asset with high frequency data. The realized volatility model proposed by Andersen [8] is representative, and the realized volatility model with high frequency data adopted by them has included plenty of intraday trading information. Hansen [9] presented Realized GARCH model to estimate the volatility, and obtained better results than other models in volatility estimation. Since all previous option pricing researches are based on low frequency data research results, high frequency data hasn’t been utilized for option pricing research yet.
Different from previous option pricing research, we take the advantages of high frequency data into account, and use high frequency data to make research of option pricing model to describe the volatility of assets with Realized GARCH model integrating high frequency data. To capture the skewness, sharp peak and fat tail distribution characteristics, we use the normal inverse gaussian (NIG) distribution to describe the distribution of assets rather than the normal distribution and build Realized-GARCH-NIG model to price the option. Final, we obtain the dynamic option pricing model based on the Realized-GARCH-NIG approach. In this paper we use the NASDAQ 100 Index Option data as research example, give an empirical analysis between the dynamic option pricing model based on the Realized-GARCH-NIG approach and the B-S option pricing model.
The structures of this article are shown in the order as follows: Section 2 is Research design, Section 3 is Empirical Methods, Section 4 is results and discussion, and Section 5 is conclusion.
2. Research Design
2.1. The Option Pricing Model
The B-S option pricing model proposed by Black and Scholes [1] is the beginning of option pricing research, and in the meanwhile, scholars represented by John [10] have developed risk neutral (martingale) option pricing theory, and derive option pricing model with risk neutral assumption. Option price model can be obtained by constructing equivalent martingale measure, and risk neutral (martingale) pricing method is now the mainstream option pricing method. So risk neutral (martingale) pricing method is utilized to research option pricing model in this paper. Let 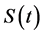 as the price of asset, and
as the price of asset, and 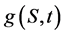 as the price of derivative product. Let
as the price of derivative product. Let 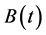 as the price of risk-free asset of a unit. If risk neutral measure Q exists, then
as the price of risk-free asset of a unit. If risk neutral measure Q exists, then 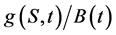 is the martingale, this paper can obtain
is the martingale, this paper can obtain
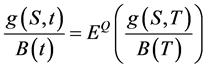 (1)
(1)
As the B-S option model,
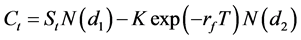 (2)
(2)
This paper can obtain
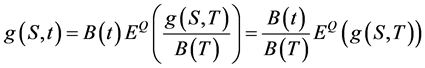 (3)
(3)
If the return of risk-free asset 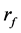 is assumed to be fixed, the price
is assumed to be fixed, the price 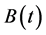 of risk-free asset of a unit at t is
of risk-free asset of a unit at t is
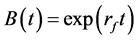 (4)
(4)
So, this paper can obtain
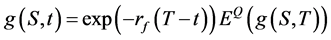 (5)
(5)
The function shows that the current price of derivative product is the discounted value of the price under risk neutral measure Q at T. According to equivalent martingale measure principle, the option value can be regarded as the function of the underlying asset, so the option that can be obtained under the underlying asset condition is as follows:
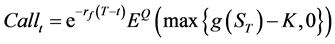 (6)
(6)
where, rf is risk-free interest rate, EQ is the expectation under risk neutral measure, T is the expiration date, 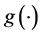 is the function of underlying asset, ST is the price of the underlying asset i at the expiration date , and K is the exercise price of option.
is the function of underlying asset, ST is the price of the underlying asset i at the expiration date , and K is the exercise price of option. 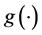 is the function of underlying asset.
is the function of underlying asset.
2.2. The Dynamic Option Pricing Model Based on the Realized-GARCH-NIG Approach
Duan [4] utilizes GARCH process to describe the volatility of assets, but the data selected by such GARCH model is low frequency data. As high frequency data is widely used in recent years, many econometricians start to directly model the volatility with high frequency data. Andersen [8] set up a realized volatility model with the high frequency data. Hansen [9] integrated the advantages of high frequency data and low frequency data in volatility estimation, and presented the Realized GARCH model. Such Realized GARCH model is as follows:
 (7)
(7)
where 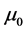 represents a mean equation, and residual error zt of the return follows standard normal distribution, and xt can be any one of realized volatility measure, and errors caused by market intraday microstructure noise and non-trading time (closing) are adjusted by coefficients
represents a mean equation, and residual error zt of the return follows standard normal distribution, and xt can be any one of realized volatility measure, and errors caused by market intraday microstructure noise and non-trading time (closing) are adjusted by coefficients 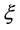 and
and




where, 

when










If X follows NIG distribution, it is simplified as:

where in, 




This paper utilizes Realized-GARCH-NIG model to describe the volatility process and distribution of assets. Duan provided a method of converting asset distribution into risk neutral distribution in his research, and this paper utilizes Realized-GARCH-NIG model to price the option by reference to Duan’s method. According to the risk neutral pricing principle, option price can be expressed as:

3. Empirical Methods
3.1. Data Sources
This paper selects the data from the database of the Chicago Board Options Exchange, and selects the NASDAQ 100 Index Option data as the research samples from June 01, 2012 to May 30, 2013. To verify the effectiveness of option pricing model proposed in this paper, this paper selects the B-S option pricing model to compare with the dynamic option pricing model based on the Realized-GARCH-NIG approach. Because of the complicated model that we used in this paper, we use the Monte-Carlo method (simulation times: 10000) to analyse the option price.
3.2. The Estimation Results
Table 1 shows the Realized-GARCH-NIG model parameter results, and Table 2 shows parameter results of the NIG distribution.
It can be seen from Table 1 that the estimated values Log, AIC and BIC can reflect the effectiveness of parameter results to a certain extent, and it can be seen from Table 2 that NIG distribution parameters are significant, and the estimated values Log, AIC and BIC can reflect the effectiveness of parameter results to a certain extent.
3.3. Comparison of Empirical Results
To quantitatively compare the pricing effect of model, this paper compares the model with three different error measurement methods. These three errors are root mean square error (RMSE), average absolute error (AAE) and average relative error (APRE) respectively. Calculation functions are as follows:
Table 1. Realized GARCH model parameters of NASDAQ 100 index option.
Table 2. NIG distribution parameter of NASDAQ 100 index options.
Table 3. Pricing errors of different models.



where, 

Table 3 shows the error comparison results. From three indexes, it can be seen that estimation error of dynamic option pricing model based on the Realized-GARCH-NIG approach is less than the B-S option pricing mode.
Above empirical results indicate that the B-S option pricing model can’t accurately describe the volatility and the characteristics of fat tail, sharp peak and skewness distribution. These defects result the deviation of option price. In this paper, the Realized GARCH model integrating high frequency data selected reflects unique advantages and the empirical results indicate that the Realized-GARCH-NIG model built in this paper is more accord with actual market situation and it can effectively describe the volatility of assets. Compared with the B-S option pricing mode, the dynamic option pricing model based on the Realized-GARCH-NIG approach is slightly deviated from actual option price and more accord with actual market situation, and can improve the accuracy and effectiveness of option pricing model.
4. Conclusion
In previous option pricing researches, low frequency data and normal distribution are often used to estimate the dynamic process of assets, those inaccurate estimation methods have a larger influence on option value estimation. Based on the advantages of high frequency data, NIG distribution, this paper utilizes the Realized- GARCH-NIG model to describe the volatility and the characteristics of fat tail, sharp peak and skewness distribution, and gets the dynamic option pricing model based on the Realized-GARCH-NIG approach. Choice the NASDAQ 100 Index Option data as research example, give an empirical analysis between the dynamic option pricing model based on the Realized-GARCH-NIG approach and the B-S option pricing model. Empirical results indicate that the dynamic option pricing model based on the Realized-GARCH-NIG approach is more accord with actual market situation, and can effectively improve the accuracy of option pricing model. With the development of financial markets, the demand of option products will certainly continue to emerge, and the option pricing model proposed in this paper provides a good reference in option pricing research. This paper will further research the application of high frequency data in option pricing model, and research high frequency nonlinear option pricing model and realization method in a dynamic market process.
Acknowledgments
Zhang Hong Lei thanks the support of the Natural Science Foundation of Sichuan Education Department (16ZB0538).
Cite this paper
Honglei Zhang,Yixiang Tian,Gaoxun Zhang, (2016) Dynamic Option Pricing Model Based on the Realized-GARCH-NIG Approach. Open Journal of Social Sciences,04,66-71. doi: 10.4236/jss.2016.43011
References
- 1. Eberlein, E. and Keller, U. (1995) Hyperbolic Distributions in Finance. Bernoulli, 281-299. http://dx.doi.org/10.2307/3318481
- 2. Cox, J.C., Ross, S.A. and Rubinstein, M. (1979) Option Pricing: A Simplified Approach. Journal of Financial Economics, 7, 229-263. http://dx.doi.org/10.1016/0304-405X(79)90015-1
- 3. Hansen, P.R., Huang, Z. and Shek, H.H. (2012) Realized Garch: A Joint Model for Returns and Realized Measures of volatility. Journal of Applied Econometrics, 27, 877-906. http://dx.doi.org/10.1002/jae.1234
- 4. Andersen, T.G., Bollerslev, T., Diebold, F.X., et al. (2003) Modeling and Forecasting Realized Volatility. Econometrica, 71, 579-625. http://dx.doi.org/10.1111/1468-0262.00418
- 5. Chorro, C., Guégan, D. and Ielpo, F. (2012) Option Pricing for GARCH-type Models with Generalized Hyperbolic Innovations. Quantitative Finance, 12, 1079-1094. http://dx.doi.org/10.1080/14697688.2010.493180
- 6. Duan, J.C. (1999) Conditionally Fat-Tailed Distributions and the Volatility Smile in Options. Rotman School of Management, University of Toronto, Working Paper.
- 7. Melick, William, R. and Charles, P. (1997) Thomas, Re-covering an Asset’s Implied PDF from Option Prices: An Application to Crude Oil during the Gulf Crisis. Journal of Financial and Quantitative Analysis, 32, 91-115. http://dx.doi.org/10.2307/2331318
- 8. Duan, J.C. (1995) The GARCH Option Pricing Model. Mathematical Finance, 5, 13-32. http://dx.doi.org/10.1111/j.1467-9965.1995.tb00099.x
- 9. Hull, J. and White, A. (1987) The Pricing of Options on Assets with Stochastic Volatilities. Journal of Finance, 42, 281-300. http://dx.doi.org/10.1111/j.1540-6261.1987.tb02568.x
- 10. Merton, R.C. (1976) Option Pricing When Underlying Stock Returns Are Discontinuous. Journal of Financial Economics, 3, 125-144. http://dx.doi.org/10.1016/0304-405X(76)90022-2
- 11. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 637- 654. http://dx.doi.org/10.1086/260062


