Advances in Pure Mathematics, 2011, 1, 238-242
doi:10.4236/apm.2011.14042 Published Online July 2011 (http://www.SciRP.org/journal/apm)
Analytical Solution of Two Extended Model Equations for
Shallow Water Waves by Adomian’s Decomposition
Method
Mehdi Safari
Islamic Azad University, Aligoodarz Branch, Department of Mechanical En gineering, Aligoodarz, Iran
Received May 22, 2011; revised June 26, 2011; accepted July 5, 2011
Abstract
In this paper, we consider two extended model equations for shallow water waves. We use Adomian’s de-
composition method (ADM) to solve them. It is proved that this method is a very good tool for shallow water
wave equations and the obtained solutions are shown graphically.
Keywords: Adomian’s Decomposition Method, Shallow Water Wave Equation
1. Introduction
Clarkson et al [1] investigated the generalized short wa-
ter wave (GSWW) equation
d
t
uxu0
x
txxtt xx
uuuu u   
 (1)
where

and

are non-zero constants.
Ablowitz et al. [2] studied the specific case 4


and 2

 where Equation (1) is reduced to
42 d0
x
txxtt xtx
uuuuu uxu 

33 d0
x
txxt txt x
uuuuxu 

(2)
This equation was introduced as a model equation
which reduces to the KdV equation in the long small
amplitude limit [2,3].However, Hirota et al. [3] exam-
ined the model equation for shallow water waves
uu (3)
obtained by substituting 3

  in (1).
Equation (2) can be transformed to the bilinear forms

23
10
3
xt txxtsx
DD DDDDDDff

 



30
x
DDD ff

20
tx x
D Dff
(4)
where s is an auxiliary variable, and f satisfies the bilin-
ear equation
xs (5)
However, Equation (3) can be transfo rmed to the bilinear
form

xt
DD D (6)
where the solution of the equation is


,2ln
x
x
uxt f (7)


,
f
xt
 
1
,1 ,
nn
n
is given by the perturbation expansion where
xtf xt 




f
(8)

is a bookkeeping non-small parameter, and where


,
nxt 1, 2,,nn,
f

 are unknown functions that will
be determined by substituting the last equation into the
bilinear form and solving the resulting equations by
equating different powers of

to zero.
The customary definition of the Hirota’s bilinear op-
erators are given by
 
,, ,
nm
tx
nm
DDab
axtbxt xxtt
tt xx

 
  

 
 
  
 
(9)
Some of the properties of the D-operators are as follows

23
22
24 22
2
22 2
63
42
2
dd,3 d
,3,ln
15 15
ttx
ttxtt
xx tx
x
x
t
xxx
Df fDDf f
uxxu uxux
ff
DffDffDDff
uuu f
ff f
Df fuuuu
f



 
 
 
 
(10)

M. SAFARI
239
 
ln,


F
where

,2
x
x
f xt
4
uxt (11)
Also extended model of Equation (2) is obtained by
the operator
x
D to the bilinear forms (4)
and (5)

30
x
D ff

 


23
1
3
xt txxxts
DD DDDDDD
(12)
where s is an auxiliary variable, and
f
satisfies the bi-
linear equation

30
x
D ff
6 0
xxx x
u uu 
4
xs
DD (13)
Using the properties of the D operators given above,
and differentiating with respect to x we obtain the ex-
tended model for Equation (2) given by
42 d
x
t xxttx tx
uuuuu uxu 
 (14)
In a like manner, we extend Equation(3) by adding the
operator
x
D

23
0
x
D ff 
6 0
xxx x
u uu 
 
Fug t
to the bilinear forms (6) to obtain

xt txx
DD DDD (15)
Using the properties of the D operators given above
we obtain the extended model for Equation(3) given by
33 d
x
t xxttx tx
uuuuu uxu 
 (16)
In this paper, we use the Adomian’s decomposition
method (ADM) to obtain the solution of two considered
equations above for shallow water waves. Large classes
of linear and nonlinear differential equations, both ordi-
nary as well as partial, can be solved by the ADM [4-15].
A reliable modification of ADM has been done by
Wazwaz [16].The decomposition method provides an
effective procedure for analytical solution of a wide and
general class of dynamical systems representing real
physical problems [4-14].This method efficiently works
for initial-value or boundary-value problems and for lin-
ear or nonlinear, ordinary or partial differential equations
and even for stochastic systems. Moreover, we have the
advantage of a single global method for solving ordinary
or partial differential equations as well as many types of
other equations.
2. Basic idea of Adomian’s Decomposition
Method
We begin with the equation

LuR u (17)
where L is the operator of the highest-ordered derivatives
with respect to t and R is the remainder of the linear op-
erator. The nonlinear term is represented by u. Thus
we get


LugtR uFu 
1
L
(18)
The inverse

is assumed an integral operator
given by

1
0
d
t
t
Lt


1
L
(19)
The operating with the operator on both sides of
Equation (18) we have


 
1
0
ufLgtRuFu

 
0
(20)
f
is the solution of homogeneous equation where
0Lu  (20)
involving the constants of integration. The integration
constants involved in the solution of homogeneous equa-
tion (21) are to be determined by the initial or boundary
condition according as the problem is initial-value prob-
lem or boundary-value problem.
The ADM assumes that the unknown function


,uxt
 
0
,,
n
n
uxtu xt




can be expressed by an infinite series of the form
(22)
F
and the nonlinear operator u

0n
n
can be decomposed by
an infinite series of polynomials given by
uA



F
(23)


,uxt nnwill be determined recurrently, and where
A
are the so-called polynomials of uu defined by
01
,,,
n
u
00
1d ,0,1,2,
!d
nii
nn
AnF un
n






 
 



42 d
6
x
txxttx t
xxxx x
LuLuuLuLuLux
LuL uuLu
 
 

(24)

3. ADM Implement for First Extended
Model of Shallow Water Wave Equation
We consider the application of ADM to first extended
model of shallow water wave equation. If Equation (14)
is dealt with this method, it is formed as
(25)
where
333
223
,, ,
xxt xxxt xxx
LLLL
x

x
txtx
 
  




1
0
d
t
t
Lt


(26)
If the invertible operator is applied to
Equation (25), then

M. SAFARI


11
6
ttt xxtt
x xxxx
LLu LLuuLu
LuL uuLu


 
240
42 d
x
x t
LuLux

2 d
x
x t
Lu Lux


0
,,
n
n
u xt








0
00
00
,
,
,d
,,
,
n
n
n
n
n
xt
uxt
u xtx
u xt
uxt



















(27)



is obtained. By this
 


1
,,0 4
6
txxt t
x xxxx
uxtuxL LuuLu
LuL uuLu

 

(28)
is found. Here the main point is that the solution of the
decomposition method is in the form of

uxt (29)
Substituting from Equation (29) in Equation(28), we find
 




1
0
00
00
,,0
4,
2,
6,
nt xxtn
n
nt
nn
x
xn t
nn
xn xxx
nn
nx
nn
uxtuxL Lu
uxtL
Lu xtL
Lu xtL
uxtL


































(30)
is found.
According to Equation (19) approximate solution can
be obtained as follows:


2
0
1s ec
,
ch
uxt c


11
21
22
cx
c






 (31)



1
3
11
sinh 21
,11
cosh 21
uxtc
c






2
11
1
1
cc
xtcc
cc
xc









1111
1
2d
6d
tx
x t
LuLu x
t


 
(32)


21
0
111
,4
xxt t
xxxx x
uxtLuuLu
LuLuuLu

 
(33)
Thus the approximate solution for first extended
model of shallow water wave equation is obtained as


2
,,uxtuxt uxt uxt (34)
The terms

012
,, ,,,uxtuxtuxtin Eq
ob (31), (32), (33).
d Extended
e-
x
uLu
(35)
where
uation (34),
01
,,
tained from Eqs.
4. ADM Implement for Secon
Model of Shallow Water Wave Equation
re we consider the application of ADM to second exH
tended model of shallow water wave equation. If Equa-
tion (16) is dealt with this method, it is formed as
33 d6
x
txxttx tx xxx
L uLuuLuLuL uxLuLu 

33
23
,, ,
x xxtxxx
L LL
tx
t
L

x
tx
 
 
  (36)
If the invertible operator

1
0
d
t
t
Lt

 is applied to
Eq

uation (35), then


33 d
6
x
tx t
xxxx x
uuLuLuLux
LuL uuLu

 
 (37)
is obtained. By this
11
tt t xxt
LLu LL



 

133 d
6
x
txxttxt
xxxx x
LLuuLuLuLux
LuL uuLu

 

(38)
is found. Here the main point is that the solution o
0n
(39)
Substituting from Equation (39) in Eq
fin

 
 
 
 
1
00
00
00
00
00
,,0 ,
3, ,
3, ,d
,,
6, ,
ntxxtn
nn
ntn
nn
x
xn tn
nn
xn xxxn
nn
nxn
nn
uxtuxLLuxt
uxtLuxt
LuxtLuxtx
LuxtLuxt
uxtL uxt















 





















(40)
,,0uxt ux
f the
decomposition method is in the form of
 
,,
n
uxtu xt


uation (38), we
d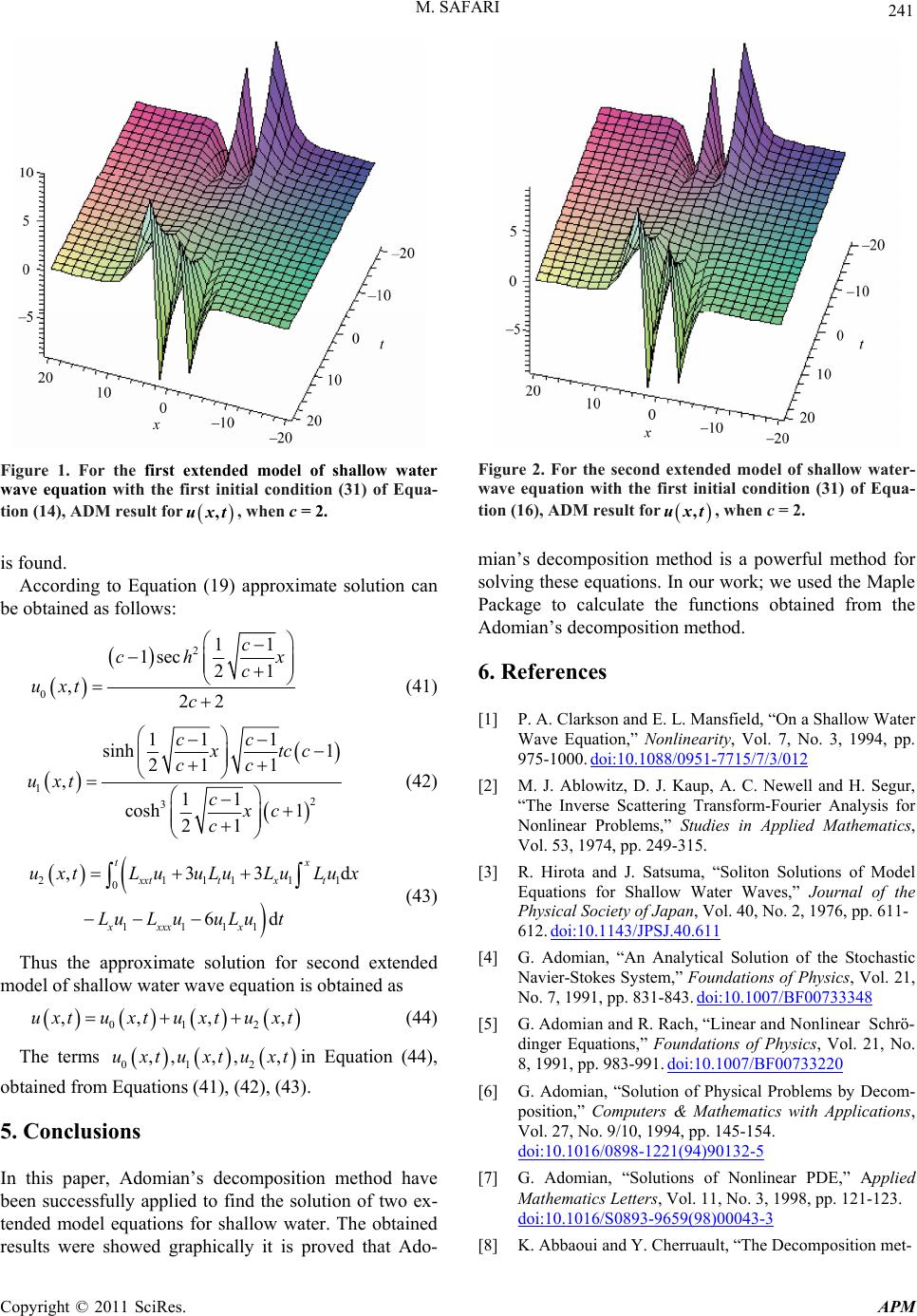




M. SAFARI
241
Figure 1. For the first extended model of shallow water
wave equation with the first initial condition (31) of Equa-
tion (14), ADM result for

uxt,, when c = 2.
is found.
According to Equation (19) approximate solution can
be obtained as follows:


2
0
1s ec
,
ch
uxt c


11
21
22
cx
c






 (41)



12
311
cosh 1
21
cxc
c






11 1
sinh 1
21 1
,
cc
xtcc
cc
uxt







 (42)
1111
3d
x
x t
LuLu x

(43)
Thus the approximate solution for second extended
model of shallow water wave equation is obtained as
 
2
,,xtu xt

2
,, ,xtuxtin Equation (44),
obtained from Equations (41), (42), (43).
5. Conclusions
In this paper, Adomian’s decomposition method
been successfully applied to find the solution of tw
tended model equations for shallow water. The obtained
results were showed graphically it is proved that Ado-

 1
0
,3
t
xxt t
uxtLuuLu

 11 11
6d
xx xx x
Lu L uuLut 
2
 
01
,,uxtuxtu

(44)
The terms

01
,,uxtu
have
o ex-
Figure 2. For the second extended model of shallow water-
wave equation with the first initial condition (31) of Equa-
tion (16), ADM result for


uxt,, when c = 2.
mian’s decomposition method is a powerful method for
solving these equa tions. In our work; we used th e Maple
Package to calculate the functions obtained from the
Adomian’s decomposition method.
6. References
[1] P. A. Clarkson and E. L. Mansfield, “On a Shall ow Wate r
Wave Equation,” Nonlinearity, Vol. 7, No. 3, 1994, pp.
975-1000. doi:10.1088/0951-7715/7/3/012
[2] M. J. Ablowitz, D. J. Kaup, A. C. Newell and H. Segur,
“The Inverse Scattering Transform-Fourier Analysis for
Nonlinear Problems,” Studies in Applied Mathematics,
Vol. 53, 1974, pp. 249-315.
pan, V
[3] R. Hirota and J. Satsuma, “Soliton Solutions of Model
Equations for Shallow Water Waves,” Journal of the
Physical Society of Jaol. 40, No. 2, 1976, pp. 611-
612.doi:10.1143/JPSJ.40.611
[4] G. Adomian, “An Analytical Solution of the Stochastic
Navier-Stokes System,” Foundations of Physics, Vol. 21,
No. 7, 1991, pp. 831-843. doi:10.1007/BF00733348
[5] G. Adomian a nd R. Rach, “Linear and Nonl inear Schrö-
dinger Equations,” Foundations of Physics, Vol. 21, No.
3-991. doi:10.1007/BF007332208, 1991, pp. 98
Solution of Physical Problems by Decom-[6] G. Adomian, “
position,” Computers & Mathematics with Applications,
Vol. 27, No. 9/10, 1994, pp. 145-154.
doi:10.1016/0898-1221(94)90132-5
[7] G. Adomian, “Solutions of Nonlinear PDE,” Applied
Mathematics Letters, Vol. 11, No. 3, 1998, pp. 121-123.
doi:10.1016/S0893-9659(98)00043-3
[8] K. Abbaoui and Y. Cherruault, “The Decomposition met-

M. SAFARI
242
hod Applied to the Cauchy Problem,” Kybernetes, Vol.
28, No. 1, 1999, pp. 103-108.
doi:10.1108/03684929910253261
[9] D. Kaya and A. Yokus, “A Numerical Comparison of
o. 6,
Partial Solutions in the Decomposition Method for Linear
and Nonlinear Partial Differential Equations,” Mathe-
matics and Computers in Simulation, Vol. 60, N
2002, pp. 507-512. doi:10.1016/S0378-4754(01)00438-4
[10] A. M. Wazwaz, “Partial Differential Equations: Methods
and Applications,” Balkema, Rottesdam, 2002.
[11] A. M. Wazwaz, “The Extended Tanh Method for New
Solitons Solutions for Many Forms of the Fifth-Order
KdV Equations,” Applied Mathematics
Vol. 184, No. 2, 2007, pp. 1002-1014 and Computation, .
doi:10.1016/j.amc.2006.07.002
[12] A. M. Wazwaz, “The Tanh–Coth Method for Solitons
and Kink Solutions for Nonlinear Pa rabolic Equations,”
Applied Mathematics and Computation, Vol. 188, No. 2,
2007, pp. 1467-1475. doi:10.1016/j.amc.2006.11.013
[13] D. D. Ganji, E. M. M. Sadeghi and M. Safari, “Applicati-
on of He’s Variational Iteration Method and Adomian’s
6
Decom-Position Method to Prochhammer Chree Equati-
on,” International Journal of Modern Physics B, Vol. 23,
No. 3, 2009, pp. 435-446.
doi:10.1142/S021797920904965
ith
[14] M. Safari, D. D. Ganji and M. Moslemi, “Application of
He’s Variational Iteration Method and Adomian’s De-
composition Method to the Fractional KdV-Burgers-
Kuramoto Equation,” Computers and Mathematics w
Applications, Vol. 58, No. 11-12, 2009, pp. 2091-2097.
doi:10.1016/j.camwa.2009.03.043
[15] D. D. Ganji, M. Safari and R. Ghayor, “Application of
He’s Variational Iteration Method and Adomian’s De-
composition Method to Saw
Equation,” Numerical Methods fo
ada-Kotera-Ito Seventh-order
r Partial Differential
Equations, Vol. 27, No. 4, 2011, pp. 887-897.
doi:10.1002/num.20559
[16] A. M. Wazwaz, “A Reliable Modification of Adomian
Decomposition Method,” Applied Mathematics and Com-
putation, Vol. 102, No. 1, 1999, pp. 77-86.
doi:10.1016/S0096-3003(98)10024-3