Modern Economy, 2011, 2, 344-353
doi:10.4236/me.2011.23038 Published Online July 2011 (http://www.SciRP.org/journal/me)
Intrinsic Motivation and Real Individual Piecewise
Linear Wages
Marie-Christine Thaize Challier
Department of Economics, Ermes, University of Paris 2, Paris, France
Received March 3, 2011; revised April 25, 2011; accepted May 6, 2011
Abstract
This paper presents a simple framework for understanding the prevalence of basic piecewise linear wages in
the real world. It extends the analysis of individual piecewise linear wages to environments in which the par-
ticipation constraint is reinforced by intrinsic motivations. It identifies a class of “acceptable” piecewise lin-
ear wages verifying both this reinforced participation constraint and the adverse selection constraint. Among
them, it restricts the characterization to a class of real-world wages. Through the advantages and drawbacks
of certain acceptable piecewise linear wages, it helps explaining why they are common in the real world even
if they are not optimal.
Keywords: Real Individual Wages; Piecewise Linear Wages; Intrinsic Motivation
1. Introduction
It is widely accepted that simple piecewise linear wages
are common in the real world (e.g., Reference [1], p. 9
and References [2-5]). 1Indeed linearity is a dominant
characteristic of real-world wages since the latter are
often (i) very basic remunerations, either constant (such
as hourly wages or other time wages) or linear in produc-
tion (piece wages) or (ii) simple remunerations such as
piecewise linear wages.2One of the reasons explaining
the importance of such simple wages is their low institu-
tional cost [13]. Another explanation, given by the stan-
dard agency model to explicate the practical relevance of
such mere wages, considers that risk-neutral principals
and agents are indifferent across a large broad range of
incentive contracts which are sometimes optimal con-
tracts linear in the outcome (for instance [9]).
The purpose of this paper is to provide an alternative
rationale regarding the significance of real piecewise
linear wages and not to characterize optimal wages. It
clarifies the reason why these wages are of high practical
relevance although non optimal. To do this it examines
the properties and implications of some of these real-
world piecewise linear wages. It underlines the interest
of positive psychology, mainly of intrinsic motivations
(see [14-17]) in the labor relations. 3Four intrinsic moti-
vations emerges here: self-confidence [23], self-esteem
[24], reciprocity [25], and self-efficacy ([26-28]). Ano-
ther distinguishing mark of our model is due the fact that
the threshold is not a predetermined quota as usually set
in the literature (References [3-5]). Here, the threshold is
endogenous. The present paper is close to the expectancy
theory (where employees expect that their efforts will
reach the desired performance) discussing the problems
caused by poorly defined targets (References [29-32]).
This paper complements the existing theoretical lite-
rature on the wage structure. Without any moral hazard
constraint, it defines “acceptable” piecewise linear wages,
i.e., wages verifying both an adverse selection constraint
and an individual rationality constraint reinforced by
intrinsic motivations. It limits the study to a class of ac-
ceptable wages widespread in the real world and charac-
terizes them. It shows that these non optimal wages can
be incentive and highlights their advantages and draw-
backs.
Section 2 presents the basic model and defines the
family of “acceptable” piecewise linear wages. Section 3
characterizes some real-world wages among this family
1Among the huge literature on the real forms of employees’ wages, see
also for instance Reference [6] and the special edition on performance
and reward [7].
2Agency theory has shown that optimal contracts can be linear in the
outcome as well as complex nonlinear contracts (e.g., quadratic wages,
p
olynomial schedules). Among the vast literature, see e.g. References
[8-10]; and for surveys regarding incentive-
b
ased theories see [11] and
[12].
3For economic studies taking into account such personal motivations
see e.g. References [18-22], and references mentioned below.

M.-C. THAIZE CHALLIER 345
and discusses the implications. Section 4 concludes with
a summary.
2. The Model
An employer (principal) has to pay a subordinate (agent)
possessing private information in a situation characte-
rized by: a static contract in the context of a single period
principal-agent framework; a contract whose remunera-
tion depends on an objective measurement of the out-
come; and a contract based on the individual perfor-
mance in the case of a tangible task. Before working, the
agent had to choose a contract, knowing not only the
technology of the firm and it potential job but also the
nature of the output-based pay. The principal and the
agent are two risk-neutral parties who reciprocate th-
rough a two-part wage system corresponding to piece-
wise linear wages.
2.1. Intrinsic Motivation, Participation and
Wages
The agent privately observes his/her ability



, 




 with

 . The profit-maximizing prin-
cipal has some probability distribution for the unknown
type parameter

. The density for this probability,

f

, is a continuous function of

with


f

> 0
for all

. Let

F

be the cumulative distribu-
tion function for the parameter

. The agent exerts a
productive effort


0,eZA , with 0Z,
supposed to be an unobservable variable, but its realized
outcome is observable for the principal. The cost of ef-
fort for the agent having the ability

is

0,ce

,
twice continuously differentiable in e and

; it satis-
fies the usual hypotheses that an increased effort rises the
cost whereas an increased ability reduces the cost:
0; 0
e
cc

 (1)
The output determines a monetary outcome denoted
y with


0, M yY y

  . It is a random variable
with

,yeg

being the probability density function
and

,Gye

the cumulative distribution function
with the usual hypothesis that, y:

0,
e
Gye   (2)
This means that an additional effort increases the like-
lihood of higher output. The technology is assumed to be
common knowledge.
The principal announces a payment schedule w:
Y  . When the agent reveals the true type para-
meter

and if the principal observes the production
level
y
, the latter pays the amount ),( yw

to the
agent. Thus the agent’s problem is:






,
max ,,d,
Y
ewygyeyce 

 


 (3)
Let


),(
ˆ
,),(
ˆwwe
 be the solution of this
problem.4 Then, the principal solves:








(.)
max, ,
ˆ ,,
dd
Y
www
f
yw ygye
y








 
According to Reference [33], the principal can achieve
the same expected profit if he chooses

,.w

in order
to induce the agent to reveal his/her true ability

. The
solution to (3) involves the adverse selection (or truth-
telling) incentive constraint:

ˆ,,w
 

 (4)
The principal’s problem can thus be stated as:






(.)
max ,
ˆ
,,dd
Y
wwfyw ygyey





under (4). The ex ante participation or individual ratio-
nality constraint is given by:





 
,,,
ˆˆ
,,d,
Ywwwygye yce
 







(5)
Let


*t

be the pure adverse selection transfer de-
fined by Reference [34] as:
    
d
ˆˆ
*, ,
s
s
tce ces


  
 (6)
where the second term of the right-hand side represents
the informational rent. This rent is negative by assump-
tion implying that *:t


is a function such that:






,,
ˆ
*, wtce    (7)
The transfer


*t

represents the expected remune-
ration amount that has to be offered to induce the agent
to reveal his/her true type in the presence of adverse se-
lection. The agent faces incentives but still earns


*t

under the optimal effort. Thus, the condition (5) can be
reinforced by the following individual rationality con-
straint:5
4Both the optimal effort ˆ
e and the optimal announcement ˆ

depend
on the true ability

and on the wage w.
5Concerning the justification of the wage level and the employer’s
agreement, it is increasingly recognized that it may be possible to in-
duce the agent to work better by introducing social preferences and
reciprocity (References [35,36]). It is also well documented that certain
employers are unwilling to accept low wage offers of employees even
when unemployment is high (References [37-39]), which is in line with
studies in psychology [40]. The sociological version of the efficiency
wage theory introduced the idea that the principal may be “generous” i
n
exchange for higher productivity (e.g., References [41,42]). The “fair-
wage-effort hypothesis” formulates that workers have their own idea
about the fair wage and reduce their effort if their actual wage is lowe
r
[43].

M.-C. THAIZE CHALLIER 346




,,
ˆ ,,d*
Ywwygye yt
  
 (8)
A distinguishing mark of this paper appears also
through (8), i.e., the individual participation constraint
reinforced by non-pecuniary motives that increase the
utility reservation. 6This constraint encompasses four
intrinsic motivations: 1) self-confidence – one’s belief in
one’s abilities; 2) self-esteem − belief regarding a per-
son’s evaluation of his/her own worth; 3) reciprocal mo-
tivation as a “cooperative job attitude” that can affect the
compensation package ([25] p. 168); and 4) self-effi-
cacy − belief about future performance; i.e., one’s belief
in one’s capability to achieve certain goals or to one’s
perception of one’s worth to perform well in specific
circumstances.
Specifically, first, the reinforced individual participa-
tion constraint assumes that the agent not only knows his
or her own level of ability but also trusts this level as
well as trusts his or her assessment on this level. This
refers to self-confidence (see for instance modern psy-
chological theories [23]). The idea here is that the agent
self-evaluates, i.e., appraises him-or herself indepen-
dently and has assurance on his or her own ability’s
evaluation.
Second, the agent asks for a wage )(*

t depending
on this ability and assesses this wage as greater than his
or her cost ),),(
ˆ (


wec . In other words, the agent
participates if he or she receives the adverse selection
transfer )(*

t, itself higher than his or her cost. At
this stage, our reinforced individual participation con-
straint refers both to self-esteem and reciprocity. Re-
garding self-esteem, it underlines that the agent knows
not only his or her ability’s level but also the valu e of
this ability. He or she is aware of his or her worth. In-
deed, according to psychologists (see [24]), self-esteem
refers to one’s evaluation of his or her own worth. It is a
basic human need corresponding to the requirement of
self worth from embracing challenges. Concerning reci-
procity, the literature (see [25] and the references therein)
has shown that reciprocal motivation of employers and
employees induce higher effort level and compensation
package.
Third, given the level and value of his or her ability,
the agent is aware of his or her capacity of reaching the
threshold. This idea comes from the theory of self-effi-
cacy reflecting a person’s evaluation of his capability of
performing well (i.e., attaining a goal, completing tasks,
or challenging) [26].
2.2. A Family of Payment Functions
Consider now a family of piecewise linear wages de-
pending on a vector of parameters

1212
,,,

  
where each parameter is a numerical function on

, i.e.
4
: 


 . The members of the wage family are de-
fined by the following “two-part wage” system (separat-
ing contract) confined to the wages composed of a base
salary and a marginal remuneration or bonus per unit of
y produced:


 
 
111
222
,;
ˆ ,;() (),
ˆ ,;(),
wy
wyy ifyy
wyy ifyy



 

 






 
 
(9)
where the threshold


ˆ,yY

  is defined by:
 




  




ˆ
11
0
22
ˆ
ˆ,,d
ˆ,,d
*
M
y
y
y
ygye y
ygye y
t


 
 






 (10)
A relevant point is that (10) stems from the equality
between the agent’s welfare

(.) ,
y
Ew ce

 in the real
situation and his/her welfare
 
,*cet


 in the pure
adverse selection situation. The constraint (10) comes
from (8) when the transfer binds the constraint. Here, the
threshold


ˆ, y

 is not a prefixed quota as usually set
in the models (References [3-5,48]). The threshold is here
endogenous and results from the assessment of the ex-
pected outcome at the point where


(.) *
y
Ew t

. In-
deed, our principal relies on her costly reciprocity as an
incentive device. Put differently, the two part wage sys-
tem (9) does not refer to the classical incentive device
with a prefixed quota. Our consideration is close to the
one formulating that firms voluntarily paid rents to elicit
non-minimum effort levels (among others, see Reference
[49]). In order to elicit more effort, the principal pays
more, on the average, if the endogenous threshold is
reached (due to the two-part wage constraint) and she
pays more than the agent’s cost (due to the welfare con-
straint). Since reciprocity-based voluntary cooperation is
an important factor in the labour relationship (for instance,
References [25,35,50]) I emphasize on the principal’s
intention to match the expected wage and the pure ad-
verse selection transfer asked by the agent through her
individual participation constraint reinforced by her self-
-efficacy.
Moreover, let us set

21
,; ,;wy wy

  for all


,
y
 , and assume that:


1
01 

;

2
01  ; (11)
6In contrast, up to now, the standard model extension about the partici-
p
ation constraint considered that nonmonetary factors lowered the
utility reservation. These factors were seen from the point of view o
f
the agent, and included idealism, ethical features, professionalism o
r
mission (References [44,45]). Concerning type-dependent participatio
n
constraints in adverse selection models see [46]. On the importance o
f
p
articipation constraints see also [47].

M.-C. THAIZE CHALLIER 347
 
12
0

  (12)
The assumption (11) indicates that the agent cannot be
the full residual claimant. This implies (12), that is, entry
fees are excluded. In addition, the existence of


ˆ,y


satisfying (10) depends on the value of


 . The fam-
ily of payment functions should be therefore restricted to


 such that

ˆ,Yy

 . The value of


ˆ,
y


also depends on

ˆ,e


, the latter being linked to

through w. Through a minor abuse of notation,


ˆ,ew

can now be written as

ˆ,e


.
Let  be the family of wages defined by (9), (10),
(11) and (12) and such that


ˆ,
y
Y  . By construction,
all members of this family satisfy the reinforced partici-
pation constraint (8). The definition also assumes that
they are incentive compatible, i.e., they induce (4).7
The following notation will prove useful. Given

 , eA and a number *
y
Y, let


,,*
y
ey 

,, *,, *ye yye y 

 be defined by:
 
 
*
0
*
,, *;
,, *;
,d
,d
M
y
y
y
ye ye
ye ye
yg yy
yg yy










(13)
Therefore (10) can be written as:
 

 
 

11
22
ˆ (.)(.), ,
ˆ
(.)1., ,
*
yGye
yGye
t
 

 






(14)
where, in order to simplify the notation, the parenthesis
(.) is explicitly:
 

ˆˆ (.),, ,,ey



 (14′)
2.3. On the Agent’s Problem
The agent’s problem (3) can now be written as:


 
  

  
  
 

1
1
2
2
ˆ
max, ,,
ˆ ,, ,,
ˆ ,, ,
ˆ
1,,,,
,
eA ye y
Gy eye
ye y
Gy eye
ce
 
 















(15)
The first order condition for

,
ˆ
e

 to be a solution
of this problem is:
 


 
 


1
2
(.)(.) ,
1
(.)(.) ,
2
ˆ,,
ˆ,
ˆ,
ee
ee
e
yGy
yGy
ce
e
e
 
 
 
 







(16)
where (.) is given by (14’) and where



,
ˆ
(.) ,
e
Gye 

 is the derivative of the function


.,(.)Gy

 evaluated at

,
ˆ
e

 . According to (14),
the agent’s problem is actually:



max ,*
eA cet


.
2.4. A Few Members of 
Let us consider Equations (14) and (16), i.e., the system
of two linear equations in the four variables,


1

 ,


2


,


1


and


2


. The set of solutions to this
system is a linear variety of dimension 2 in 4


. There
are potentially an infinite number of acceptable members
in

. The term acceptable means that the piecewise
linear wage satisfies (4) and (8). I list some members or
subsets of

below; for expositional simplicity, I limit
the study to five of them among the above-mentioned real
piecewise linear wages. All of them solve (14) and (16).
They define an acceptable contract payment function only
if they meet the restrictions (11) and (12) and if


,
ˆYy


.
Case 1.




12
0  

;








   

1*,
1,, ;
,,,
ˆ,
ˆˆˆ ,, ,
e
e
tc
Gee
G
e
y
yey e
 


















   

2*,
,, .
,,,
ˆ,
ˆˆˆ
,, ,
e
e
tc
Gee
G
e
y
yey e
 









Case 2.
 



  
12
,
,,
ˆ,
0; ˆˆ
,,
e
e
ce
ye y








 ;






  
  
12
*
,
,,
,,;
ˆ,
ˆˆ ,,
ˆˆ
,,
e
e
t
ce
ye y
ye y
 




 







Case 3. The set of solutions to (14) and (16) with


10


. For example, if the system is solved for


2

 and


2

 , we obtain:
7See References [51,52] pp. 257-262.

M.-C. THAIZE CHALLIER 348
    








 


21
1ˆˆˆ ˆ
,,, ,,,*1, ,,,
;
e e
GyeyetGy eece









 





 

  

     

 

21
1ˆˆ
,, *,,,,
ˆˆˆˆ ˆˆ
(,,,,,,) ,,,,,,
1
e
ee
Gyeety ey
Gyeyece yey
 
  
 



 


 


where
 


.. .1
ee
yG yG

 .
Case 4. The set of solutions to (14) and (16) with




12


 . The system can be solved for


2


,


1


and


2


. This yields:
 

 
  
ˆ,, ,
1
2ˆˆ
,,, ,
eeye
e
ye y
e
c

 
 






;









  
  
12 1
,,
,,,
,,
ˆ,1ˆˆ
*,,
ˆˆ
,,
e
ce
eey
e
yyey
ye y
e
t
 





 



 






.
Setting


1

  0, we get Case 2.
Case 5.

2

  0;

1

  0;
 

 











1
ˆˆˆ (,,,, ,,)*()1(,,.
ˆˆˆ 1,,, ,,,,,,,
ee
ee
Gy eyetGy ee
Gy eey eGy
c
eyeye
  


 








 






;













   


2
ˆ
,*, ,,
ˆˆˆ
1, ,,,,, ,,,,
e
ee
e
ye tyee
Gy ee
c
ye Gyeyeye




  


 




.
3. Characterization and Discussion
Prior to establishing the propositions, this section defines
the following rewards that will be useful to explain some
characteristics of the wages.
Definition 1.
(i) The reward

R

depends on whether


ˆ
y

is
reached or not:
 
21
ˆˆ
,;, ;Rwywyy

   .8 (17)
(ii) The rewards


1
R

and


2
R

depend on the
difference between


.w and


*t

:
 
 
11
22
;
.
ˆ ,;*
ˆ ,; *
Rwyyt
Rwyt








(18)
To improve the understanding of the rewards


1
R

-
and

2
R

the value of


*t

has been positioned in
the figures and represented by the horizontal dotted line.9
The following propositions characterize some wide-
spread piecewise linear wages. (All these wages are de-
picted in the figures displayed in the appendix).
Proposition 1. Let 4 : 

 ,

:*t 


 ,
and


ˆ,:y


 be functions such that,


:
1) The vector

has the values given in Case 1. If
these values satisfy (11) and (12), then they define an
acceptable wage, called PL1, given by:


 



 




 



 

 

,;
ˆ
1,,(,),
*ˆˆˆ
,,, ,,,
ˆ,
ˆ ,, ,,
*ˆˆˆ
(,,, ,,,
ˆ,
e
e
e
e
wy
Gy eee
tGye
c
c
ye
if yy
Gy eee
tGyey e
if yy




 

 

  





















(19-PL1)
2) The vector

has the values given in Case 2. If
these values satisfy (11) and (12), then they define an
acceptable wage, called PL2, given by:
8The symbol  means here that the value of y is smaller but very
close to ˆ y.
9The position of


*t

on the figures obviously depends on the steep-
ness of the wages and on the lengths of the segments [0,


ˆ,y


[ and

ˆ,,
M
yy  

where
M
y is the maximum value of the production y.

M.-C. THAIZE CHALLIER 349

 
  
   
 

  
 



ˆ(,), ˆ
*,,if,
ˆˆ
,,, ,
,; ˆ,, ˆ
*,,if,
ˆˆ ,,, ,
ˆˆ
,,
ˆˆ
,,
e
e
e
e
e
teyy
ye y
wy e
tyy
ye y
c
c
ye y
yye y
  
 
  


 
 
















(20-PL2)
3) The vector

has the values given in Case 3. If
these values satisfy (11) and (12), then they define an acceptable wage, called PL3, given by:

 
   

 

 




1
1
11
ˆ if ,
1
,;..*. (1..
ˆ
..*......if,
ee
eee
yy
wyGt G yc
cGt yGyyy

 










  

(21-PL3)
Proof. In each of these three cases, it is easily verified
that the given values for the parameters satisfy (14) and
(16).
Implication 1. Proposition 1 and Definition 1 assign
the following rewards:
 for wage PL1:
 
12
00,, 0RR R  .
 for wage PL2:
 
12
00,, 0RR R  .
 for wage PL3: (a)
 
12
00,, 0RR R  .
(a’)
 
12
00,, 0RR R  .
Proposition 1 refers to acceptable contracts with a con-
stant wage below the threshold

ˆ,y

 . The piecewise
linear wage PL1 (given in (19) and depicted in Figure 1)
includes two constant wages and offers


R 


0.(.) (.)
ee
cG 10In addition,

2*t


 

1

  under 0
e
c and 0
e
G. Explicitly, when
the real output y is lower (resp. higher) than the thresh-
old

,
ˆ y

 , the wage received is lower (resp. higher)
than the pure adverse selection transfer

*t

, the latter
being here the reservation wage. It is necessary to produce

,
ˆ
yy

  in order to obtain



*,;twy


  (see
Table 1). The step-function wage PL1 performs well
since it encourages the agent to achieve the threshold.
Nevertheless the agent is not stimulated to exceed the
threshold since

20
 .
The piecewise linear wages PL2 and PL3 (given in (20)
and (21)) present a positive base salary

1


, a con-
stant wage below the threshold

ˆ,y

 , and a piece
wage beyond

ˆ,y

 . The wage PL2 (Figure 2)
presents a positive reward


R

. In addition, if


*t

has the value given in Figure 2 then

10R


and

20R
  (see Implication 1 and Table 1). Put diffe-
rently, at

ˆ,yy

 , the wage

2,;wy

 will be
equal to the pure adverse selection transfer


*t

and
thus

20R
 . Therefore, given that the agent asks for
at least


*t

, PL2 incite him or her to achieve


ˆ,y

 .
The convex wage PL3 may be the noncontinuous
convex wage PL3a (see Figure 3a) or the continuous
convex wage PL3a’ (see Figure 3a’). The analysis is
straightforward in the case of the piecewise linear wage
PL3a whose nature gives

0R   and where intrinsic
motivations lead the agent to reach the threshold
(


10R


and


20R
 ). In other words, at the
threshold


ˆ,y

 , the wage received

,;wy

 is
higher than the reservation wage

*t

(see Implica-
tion 1 and Table 1).
Figure 1. Wage PL1.
Table 1. Summary of the comparison between the real wage
and the reservation wage for some of acceptable piecewise
linear wages.
Cases PL1, PL3a, PL4:


,; *wyt 

 at


ˆ,yy

 ;


,; *wy t 

 at

ˆ,y


Case PL2:


,; *wyt 

 at

ˆ,y


Case PL3a’:


,; *wyt 

 at

ˆ,
B
yyy 


Case PL5:


,; *wy t 

 at


ˆ,
A
yyy

 
10The positivity of

R

may be explained by the fact that extra
effort both raises the principal’s utility via the increase in the probabil-
ity of reaching the threshold (since0
e
G) and reduces the agent’s
utility via the increase of the cost (since 0
e
c).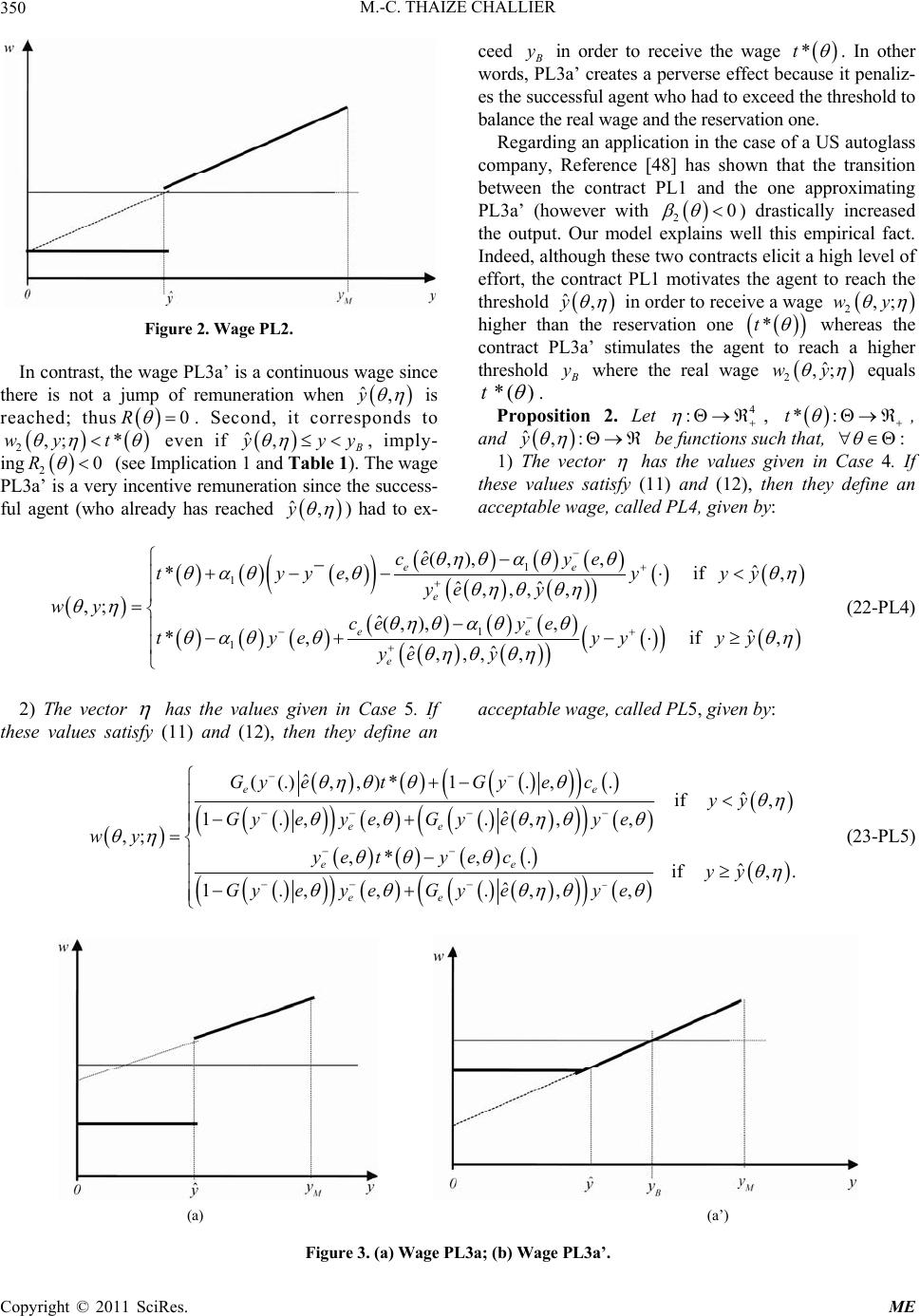

M.-C. THAIZE CHALLIER 350
Figure 2. Wage PL2.
In contrast, the wage PL3a’ is a continuous wage since
there is not a jump of remuneration when


ˆ,y

 is
reached; thus

0R  . Second, it corresponds to

2,; *wy t


 even if

ˆ,
B
y
yy   , imply-
ing

20R
  (see Implication 1 and Table 1). The wage
PL3a’ is a very incentive remuneration since the success-
ful agent (who already has reached

ˆ,y

 ) had to ex-
ceed
B
y in order to receive the wage

*t

. In other
words, PL3a’ creates a perverse effect because it penaliz-
es the successful agent who had to exceed the threshold to
balance the real wage and the reservation one.
Regarding an application in the case of a US autoglass
company, Reference [48] has shown that the transition
between the contract PL1 and the one approximating
PL3a’ (however with


20
 ) drastically increased
the output. Our model explains well this empirical fact.
Indeed, although these two contracts elicit a high level of
effort, the contract PL1 motivates the agent to reach the
threshold


ˆ,y

 in order to receive a wage


2,;wy


higher than the reservation one


*t

whereas the
contract PL3a’ stimulates the agent to reach a higher
threshold
B
y where the real wage

2ˆ
,;wy

 equals
)(*

t.
Proposition 2. Let 4
: 

 ,

:*t 


 ,
and


ˆ,:y


 be functions such that,




:
1) The vector

has the values given in Case 4. If
these values satisfy (11) and (12), then they define an
acceptable wage, called PL4, given by:










 


 
 




1
1
1
1
ˆ(, ),,ˆ
*, if,
ˆˆ
,,, ,
,; ˆ(, ),,ˆ
*, if,
ˆˆ
,,, ,
e
e
e
e
ee
eye
tyye yyy
ye y
wy eye
tye yyyy
ye y
c
c
 




  



 












 






(22-PL4)
2) The vector

has the values given in Case 5. If
these values satisfy (11) and (12), then they define an acceptable wage, called PL5, given by:

  








 


 
 



 


 
ˆ
((.) ,,)*1.,.
ˆ
if ,
ˆ 1.,, .,,,
,;
,*,.ˆ
if, .
ˆ
1.,, .,,,
ee
ee
ee
ee
Gy etGyeyy
GyeyeG yeye
wy ye tyeyy
GyeyeG yey e
c
c
 


 
 


 






 











(23-PL5)
(a) (a’)
Figure 3. (a) Wage PL3a; (b) Wage PL3a’.

M.-C. THAIZE CHALLIER 351
Proof. The values for the parameters satisfy (14) and
(16). The proof is straightforward.
Implication 2. Proposition 2 and Definition 1 assign
the following rewards:
 for wage PL4:
 
12
00,, 0RR R  .
 for wage PL5:
 
1
,00RR   between A y
and

ˆ,y


,

20R
 .
Proposition 2 deals with acceptable contracts without a
constant wage below the threshold. The piecewise linear
wage PL4 (given in (22) and represented in Figure 4)
includes a positive base salary (

0  ) and two in-
creasing wages. It is incentive not only because the agent
receives the reward

0R   if

ˆ,yy


 and is in-
crementally penalized below


ˆ,y


but also because it
encourages the agent to reach

ˆ,y


in order to obtain
more than

*t

.
Up to now, the agent who satisfies his or her intrinsic
motivations had to attain the threshold (wages PL1, PL2,
PL3a, and PL4) or to exceed it (wage PL3a’). Such wag-
es are incentive. This explains why they are common in
the concrete world despite their non-optimality. In con-
trast, the wage PL5 is presented here as a counterexam-
ple regarding the value of


1
R

(Implication 2). The
continuous concave wage PL5 (given in (23) and de-
picted in Figure 5) is composed of a base salary equals
to zero, an increasing wage until the threshold, and a
constant compensation beyond it. Even if the threshold is
not reached, the agent receives a remuneration higher
than the pure adverse selection transfer. In formal terms,
if

ˆ,
A
yyy 

 then


1,; *wy t


. Other-
wise stated, although PL5 satisfies the reinforced partic-
ipation constraint and the adverse selection constraint,
the agent is not stimulated to achieve the threshold

ˆ,y


since his or her reservation wage


*t

is
already satisfied at A y (see Implication 2 and Table 1).
This is the type of perverse effect where the real wage
favors the agent who does not reach the threshold.
Figure 4. Wage PL4.
Figure 5. Wage PL5.
To sum up, among the infinite number of acceptable
wages, the paper has selected and characterized six wag-
es found in the real world. Five of these six wages are
shown to be incentive (PL1, PL2, PL3a, PL3a’, and PL4).
However, the incentive continuous convex wage PL3a’
creates a perverse effect since it penalizes the successful
agent who had to exceed the threshold to balance the real
wage and the reservation one. Finally, the concave wage
PL5 is not incentive; it induces a second perverse effect
where the agent who does not reach the threshold is re-
warded.
The findings of this paper should not be interpreted to
endorse the generalization of output-contingent compen-
sations. They only help explaining the real-world piece-
wise linear wages. This empirical fact may be understood
through the advantages and drawbacks of such payments.
Among their advantages, the following ones are note-
worthy. Regarding the agent, the individual participation
constraint is reinforced by non-pecuniary motivations
that increase the reservation wage. A second advantage
occurs as regards the wages PL1, PL3a and PL4 since, at


ˆ,y


, the agent enjoys a wage

,;wy

 strictly
higher than the reservation wage

*t

. (Concerning
the wage PL5,


,;wy

 is even strictly higher than


*t

before reaching the threshold). As regards the
drawbacks of these wages, the findings have highlighted
two perverse effects. A first drawback relates to the prin-
cipal through the wage PL5 whereas the second one af-
fects the agent through the wage PL3a’.
4. Conclusions
Through a simple model, this paper contributes to the
understanding of the prevalence of several non optimal
piecewise linear wages. It enriches theories of compen-
sation by hypothesizing new determinants of pay (th-
rough intrinsic motivations reinforcing the classical indi-
vidual participation constraint) and by identifying and

M.-C. THAIZE CHALLIER 352
characterizing some subsequent “acceptable” piecewise
linear wages. By definition, the term “acceptable” means
that the wages verify the adverse selection constraint and
a participation constraint reinforced by intrinsic motiva-
tions such as agent’s self-confidence, self-esteem, reci-
procity, and self-efficacy. Then, the paper defines the
wage structure – noncontinuity or continuity, convexity
or concavity, that is, the compensation gap (i.e., positive
or negative rewards) between the real wages and the res-
ervation ones. It shows that some acceptable piecewise
linear wages can be incentive.
The recent years saw a significant increase in the use
of simple output-contingent payments over the world.
Thus, the present theoretical findings may explain this
empirical fact through the advantages and drawbacks of
such payments.
5. Acknowledgements
I am grateful to Michel Truchon for generous and very
helpful comments and suggestions. I also benefited from
the comments of the conference participants at the Euro-
pean Economic Association meeting at Budapest and of
the seminar participants at University of Laval on earlier
drafts of this paper. Of course, the usual caveats apply.
6. References
[1] O. D. Hart and B. Holmström, “The Theory of Con-
tracts,” Advances in Economic Theory: Fifth World Con-
gress, Cambridge University Press, Cambridge, 1987.
doi:10.1017/CCOL0521340446.003
[2] E. F. Fama, “Time, Salary, and Incentive Payoffs in La-
bor Contracts,” Journal of Labor Economics, Vol. 9, No
1, 1991, pp. 25-44. doi:10.1086/298257
[3] E. P. Lazear, “Personnel Economics,” The MIT Press,
Cambridge, 1996.
[4] E. P. Lazear, “Personnel Economics for Managers,”
Wiley, New York, 1998.
[5] E. P. Lazear, “Personnel Economics: Past Lessons and
Future Directions,” Journal of Labor Economics, Vol. 17,
No. 2, 1999, pp. 199-236. doi:10.1086/209918
[6] D. Parent, “Methods of Pay and Earnings: A Longitudinal
Analysis,” Industrial and Labor Relations Review, Vol.
53, No. 1, 1999, pp. 71-86. doi:10.2307/2696162
[7] D. Collings, T. Dundon and M. Marchington (Eds.),
“Human Resource Management Journal,” Special Edition
on Performance and Reward, Vol. 18, No. 4, 2008.
[8] P. Picard, “On the Design of Incentive Schemes under
Moral Hazard and Adverse Selection,” Journal of Public
Economics, Vol. 33, No. 3, 1987, pp. 305-331.
doi:10.1016/0047-2727(87)90058-2
[9] J.-J. Laffont and J. Tirole, “The Dynamics of Incentive
Contracts,” Econometrica, Vol. 56, No. 5, 1988, pp. 1153-
1175. doi:10.2307/1911362
[10] F. Balmaceda, “Uncertainty, Pay for Performance, and
Asymmetric Information,” Journal of Law, Economics
and Organization, Vol. 25, No. 2, 2009, pp. 400-441.
doi:10.1093/jleo/ewn022
[11] R. Gibbons, “Incentives in Organizations,” Journal of
Economic Perspectives, Vol. 12, No. 4, 1998, pp. 115-
132.
[12] C. Prendergast, “The Provision of Incentives in Firms,”
Journal of Economic Literature, Vol. 37, 1999, pp. 7-63.
doi:10.1257/jel.37.1.7
[13] B. Holmström and P. Milgrom, “Aggregation and Linear-
ity in the Provision of Intertemporal Incentives,” Econo-
metrica, Vol. 55, No. 2, 1987, pp. 303-328.
doi:10.2307/1913238
[14] E. L. Deci, “Intrinsic Motivation,” Plenum Press, New
York, 1975.
[15] E. L. Deci and R. M. Ryan, “Intrinsic Motivation and
Self-Determination in Human Behavior,” Plenum Press,
New York, 1985.
[16] M. E. P. Seligman, “Authentic Happiness: Using the New
Positive Psychology to Realize Your Potential for Lasting
Fulfillment,” Free Press, New York, 2002.
[17] C. Peterson and M. E. P. Seligman, “Character Strengths
and Virtues: A Handbook and Classification,” Oxford
University Press, Oxford, 2004.
[18] B. Frey, “Not Just for the Money. An Economic Theory
of Personal Motivation,” Edward Elgar, Cheltenham, 1997.
[19] D. Kreps, “Intrinsic Motivation and Extrinsic Incentives,”
American Economic Review, Vol. 87, No. 2, 1997, pp.
359-364.
[20] U. Gneezy and A. Rustichini, “Pay Enough or Don’t Pay
at All,” Quarterly Journal of Economics, Vol. 115, No. 3,
2000, pp. 791-810. doi:10.1162/003355300554917
[21] R. Bénabou and J. Tirole, “Intrinsic and Extrinsic Moti-
vation,” Review of Economic Studies, Vol. 70, 2003, pp.
489-520.
[22] R. Bénabou and J. Tirole, “Incentives and Prosocial Be-
havior,” American Economic Review, Vol. 96, No. 5,
2006, pp. 1652-1678.
[23] R. J. Corsini, “The Dictionary of Psychology,” Routledge,
Brunner, 1999.
[24] N. Branden, “The Psychology of Self-Esteem,” Bantam,
New York, 1969.
[25] E. Fehr and S. Gachter, “Fairness and Retaliation: The
Economics of Reciprocity,” Journal of Economic Per-
pectives, Vol. 14, No. 3, 2000, pp. 159-181.
doi:10.1257/jep.14.3.159
[26] A. Bandura, “Self-Efficacy: The Exercise of Control,”
Freeman & Co., New York, 1997.
[27] A. Bandura and E. A. Locke, “Negative Self-Efficacy and
Goal Effects Revisited,” Journal of Applied Psychology,
Vol. 88, No. 1, 2003, pp. 87-99.
doi:10.1037/0021-9010.88.1.87
[28] J. B. Vancouver, K. M. More and R. J. Yoder, “Self-
-Efficacy and Resource Allocation: Support for a Discon-
tinuous Model,” Journal of Applied Psychology, Vol. 93,

M.-C. THAIZE CHALLIER 353
No. 1, 2008, pp. 35-47. doi:10.1037/0021-9010.93.1.35
[29] V. H. Wroom, “Work and Motivation,” Wiley, New York,
1964.
[30] L. W. Porter and E. E. Lawler, “Managerial Attitudes and
Performance,” Dorsey, Homewood, 1968.
[31] E. A. Locke and G. P. Latham, “A Theory of Goal Set-
ting and Task Performance,” Prentice-Hall, Englewood
Cliffs, 1990.
[32] A. Furnham, “The Psychology of Behavior at Work: The
Individual in the Organization,” Psychology Press, Hove,
1997.
[33] R. B. Myerson, “Optimal Coordination Mechanisms in
Generalized Principal-Agent Problems,” Journal of Ma-
thematical Economics, Vol. 10, 1982, pp. 67-81.
doi:10.1016/0304-4068(82)90006-4
[34] J. A. Mirrlees, “An Exploration in the Theory of Opti-
mum Income Taxation,” Review of Economic Studies,
Vol. 38, No. 2, 1971, pp. 175-208. doi:10.2307/2296779
[35] E. Fehr, S. Gächter and G. Kirchsteiger, “Reciprocal
Fairness and Noncompensating Wage Differentials,”
Journal of Institutional and Theoretical Economics, Vol.
152, No. 4, 1996, pp. 608-640.
[36] E. Fehr and K. M. Schmidt, “Fairness, Incentives, and
Contractual Choices,” European Economic Review, Vol.
44, No. 4-6, 2000, pp. 1057-1068.
doi:10.1016/S0014-2921(99)00046-X
[37] T. F. Bewley, “Why Not Cut Pay?” European Economic
Review, Vol. 42, No. 2, 1998, pp. 459-490.
doi:10.1016/S0014-2921(98)00002-6
[38] E. Fehr and A. Falk, “Wage Rigidity in a Competitive
Incomplete Contract Market,” Journal of Political Eco-
nomy, Vol. 107, No. 1, 1999, pp. 106-134.
doi:10.1086/250052
[39] M. Dufwenberg and G. Kirchsteiger, “Reciprocity and
Wage Undercutting,” European Economic Review, Vol.
44, No. 4-6, 2000, pp. 1069-1078.
doi:10.1016/S0014-2921(99)00047-1
[40] M. Argyle, “The Social Psychology of Work,” 2nd Ed-
tion, Penguin, Harmondsworth, 1989.
[41] G. A. Akerlof, “Labor Contracts as Partial Gift Exch-
ange,” Quarterly Journal of Economics, Vol. 97, No. 4,
1982, pp. 543-569. doi:10.2307/1885099
[42] G. A. Akerlof and J. Yellen, “Efficiency Wage Models of
the Labor Market,” Cambridge University Press, Cam-
bridge, 1986. doi:10.1017/CBO9780511559594
[43] G. A. Akerlof and J. Yellen, “The Fair Wage-Effort Hy-
pothesis and Unemployment,” Quarterly Journal of
Economics, Vol. 105, No. 2, 1990, pp. 255-283.
doi:10.2307/2937787
[44] J. Q. Wilson, “Bureaucracy: What Government Agencies
Do and Why They Do it,” Basic Books, New York, 1989.
[45] T. Besley and M. Ghatak, “Competition and Incentives
with Motivated Agents,” American Economic Review,
Vol. 95, No. 3, 2005, pp. 616-636.
doi:10.1257/0002828054201413
[46] B. Jullien, “Participation Constraints in Adverse Selec-
tion Models,” Journal of Economic Theory, Vol. 93, No.
1, 2000, pp. 1-47. doi:10.1006/jeth.1999.2641
[47] P. Oyer, “Why Do Firms Use Incentives That Have No
Incentive Effects,” Journal of Finance, Vol. 59, No. 4,
2004, pp. 1619-1650.
doi:10.1111/j.1540-6261.2004.00674.x
[48] E. P. Lazear, “Performance Pay and Productivity,” Ame-
rican Economic Review, Vol. 90, No. 5, 2000, pp. 1346-
1361. doi:10.1257/aer.90.5.1346
[49] E. Fehr, E. Kirchler, A. Weichbold and S. Gächter,
“When Social Norms Overpower Competition: Gift Ex-
change in Experimental Labor Markets,” Journal of La-
bor Economics, Vol. 16, No. 2, 1998, pp. 324-351.
doi:10.1086/209891
[50] E. Fehr and A. Falk, “Psychological Foundations of In-
centives,” European Economic Review, Vol. 46, No. 4-5,
2002, pp. 687-724. doi:10.1016/S0014-2921(01)00208-2
[51] J.-J. Laffont and J. Tirole, “Using Cost Observation to
Regulate Firms,” Journal of Political Economy, Vol. 94,
No. 3, 1986, pp. 614-641. doi:10.1086/261392
[52] D. Fudenberg and J. Tirole, “Game Theory,” MIT Press,
Cambridge, 1991.