Received 13 January 2016; accepted 26 February 2016; published 2 March 2016

ABSTRACT

Numerical Finite-element method (FEM) based algorithms have been widely applied for the reconstruction of the photoacoustic image. As compared with the traditional analytic methods, the FEM based methods can be easily used to deal with problems with irregularly shaped imaging domain. However, the FEM based algorithms are usually computationally intensive because repeated manipulations of matrices with larger size are needed during the reconstruction process. To tackle such a problem, a novel method is proposed for reducing the size of the matrix to be inversed during the reconstruction process and hence speed up the inverse reconstruction without any sacrifice of the reconstruction accuracy.

Keywords:

Inverse Problems, Medical and Biological Imaging, Image Reconstruction Techniques

1. Introduction

Photoacoustic tomography (PAT) is an emerging biomedical imaging technique for visualizing tissue structure and function with excellent ultrasound resolution and excellent optical contrast [1] [2]. PAT is actually concerned with an inverse problem where a single pulsed light beam illuminates an object and the light-included acoustic fields in multiple locations around the object are measured.

The geometry of the object and spatial distribution of the optical property can be obtained from the measured scattered fields by using a reconstruction algorithm. For reconstructing the photoacoustic images, a proper physical model should be used for describing the propagation of light-induced acoustic wave in tissues. In most existed photoacoustic tomography reconstruction algorithms, the Helmholtz-like equation has been often used as an accurate model. Among the above mentioned algorithms [3]-[7], some rely on analytical solutions to the photoacoustic wave equation in a regularly shaped imaging domain without appropriate boundary condition applied. These algorithms can usually be implemented very fast. However, they can only be used for PAT reconstruction in the regularly shaped imaging domain and are not valid for the development algorithms for more sophisticated tissue excitation and data collection strategies. Algorithms of the other type are based on the finite element method which can be used to solve the photoacoustic wave equation more accurately in arbitrary problem geometry. Although these methods can somewhat alleviate the limitation as mentioned above, the reconstruction should be implemented with iterative optimization strategies such as the iterative Newton method [8]. These algorithms are computationally intensive especially when the number of the finite element nodes is relatively large.

To reduce the computational requirement and speed up the reconstruction process of the finite-element-based algorithms, we propose a matrix transform method that can significantly reduce the size of the matrix to be inversed in the reconstruction process and accelerate iterative procedure without any sacrifice of the reconstruction accuracy.

2. Reconstruction Algorithm and the Matrix Transform

2.1. Acoustic Forward Problem

The acoustic forward problem is to compute the boundary pressure from a proper physical model describing the propagation of the acoustic wave when the absorbed optical energy density is given. Because the optical propagation, absorption, and conversion to heat typically occur on a timescale much shorter than the mechanical relaxation, the local tissue mass density does not change significantly until all the optical energy has been converted to heat. Hence, it is often assumed that the heating occurs instantaneously. Under this assumption, the acoustic propagation in the frequency domain can be described with the following Helmholtz equation together with the second-order absorption boundary condition:

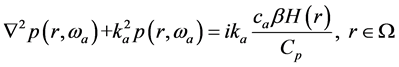(1)

(2)

where is the adsorbed optical energy density, 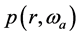is the pressure wave with frequency 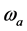and at point r, 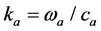is the wave number described the angular frequency, is the speed of acoustic wave in the medium, 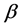is the thermal expansion coefficient, 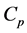is the specific heat, and

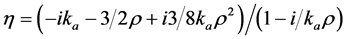(3)

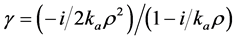(4)

with 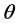being the angular coordinate at a radial position.

2.2. FEM Implementation of the Acoustic Forward Model

Upon expanding the and in terms of a set of basis functions, i.e.,

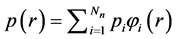(5)

(6)

and utilizing the associated boundary conditions in Equation (2), we can obtain the following finite-element discretization of Equation (1)

(7)

where the components of matrix A and b are expressed as

(8)

(9)

Vectors and can be expressed in terms of their real and imaginary components as

(10)

(11)

2.3. Reconstruction Algorithm

The inverse problem of PAT is based on the minimization of the following weighted least squares:

(12)

where and are the measured and calculated pressure wave data, represents the parameter distribution (or ) at the previous iteration, is the regularization parameter. To solve the optimization equation in Equation (12) with the gradient-based algorithm, we obtain the iterative equation as follow:

(13)

where (dimension: with being the number of acoustic field data in boundary locations, being the numbers of finite element nodes) is the Jacobian matrix, represents the distribution of or. Here, the regularization scheme is adopted to stabilize the decomposition of, is the identity matrix, and the regularization parameter is determined by combined Marquardt and Tikhonov regularization scheme [9]. The reconstruction algorithm here uses the Newton method to update a guess of initial optical and acoustic property distribution iteratively via the solution of Equations (7) and (13) so that an objective function composed of a weighted sum of the squared difference between computed and measured acoustic pressures for all frequencies can be minimized.

2.4. Matrix Transform Strategy

The reconstruction process involves the matrix inversion of. The size of this matrix is. Since N is usually very large and hence such an inversion process is usually computationally intensive. In order to reduce the computation complexity of the reconstruction algorithm, we proposed a matrix transform strategy for Equation (13) as follow:

(14)

As can be seen from Equation (14), after the matrix transform procedure, the matrix inversion can be performed with respect to the matrix of rather than that of. The size of the former matrix is rather than for the latter one. Usually, is much larger than and hence the computational requirements for matrix inversion can be significantly reduced upon performing the above mentioned matrix transform procedure.

3. Result and Analysis

As discussed above, the PAT image can be reconstructed with an iterative scheme in Equations (7) and (13). The inverse problem in PAT is the acoustic inverse initial value problem in which the initial absorbed optical energy density is estimated when measured acoustic wave on the detectors are given. The simulated distribution of the initial absorbed optical energy density is shown in Figure 1. The absorbed optical energy density for both the target and the background are shown in the Table 1. Other parameters used in Equation (1) are

, ,. In the algorithm, the speed of reconstruction is dependent on the number of the element nodes. So two finite-element-mesh with different grids as shown in Figure 2 are used for the simulation. The numbers of nodes in the fine and coarse mesh of triangular elements are 2097 and 541, respectively.

In our simulation, 32 ultrasonic transducers distributed evenly around the phantom (as shown in Figure 1) are used to receive the acoustic pressure. The k-space method is used to simulate propagation of the pressure wave through the domain based on the initial absorbed optical energy density. Since our reconstruction is performed in the frequency domain, the recorded time-varying data are first transformed into the frequency domain. We only choose components with frequencies lower than 30 MHz for our reconstruction because components with frequencies higher than this range are very small. With these simulated data in the frequency domain, the PAT image is reconstructed with the iterative scheme in Equations (7) and (13).

3.1. Reconstruction

The PAT images are reconstructed with the algorithm as the discussed before. The reconstruction is implemented in Matlab R2010a and a personal computer with 2.7 GHz Intel Core dual-core CPU and 8 G bytes of RAM. Each reconstruction result is obtained after take 5 iterations. In order to evaluate the performance of the reconstruction, the relative running time reduction and the mean square error (MSE) of defined as follow are used:

, (15)

where and is the running time before and after the matrix transform. is the number of vertex nodes. and are the real reconstruction and real absorbed optical energy density.

3.1.1. Reconstruction with the Coarse Mesh

The proposed algorithm is first evaluated in the coarse mesh (1016 elements and 541 nodes). Figure 3 gives the reconstruction results of the target with two equations, where 1) is solved with the traditional Equation (13), 2) is solved with the transformed Equation (14). From images in this figure and the MSE in Table 2, we can see that the reconstruction with two equations has the same results. The target can be properly recovered by both iterative equations. The transform of traditional equation do not cause any sacrifice on the reconstruction results. The running time of two methods are summarized in Table 2. From this table, we can see that the proposed method is more efficient than the traditional one. The proposed one saves 29.43 percent of time than the traditional method.

3.1.2. Reconstruction in the Fine Mesh

The proposed algorithm is also evaluated in the fine mesh (4064 elements and 2097 nodes). Figure 4 gives the reconstruction results of the target upon solving respectively, Equations (13) and (14), where (a) is the result from Equation (13) while (b) is the result from the transformed equation of (14). From images in this figure and the MSE in Table 3, we can draw the same conclusion as that from images in Figure 3. The running time of two methods in the fine mesh are summarized in Table 3. As can be seen from this table, the running times both increase significantly as compared with that in the coarse mesh. The relative reduction of time between these two methods also grows larger in the fine mesh. The matrix transform even takes half of the time spent by the traditional one.

4. Conclusion

In this paper, we propose a matrix transform method for reducing the computational requirements in the reconstruction of the photoacoustic tomography. The results of the simulations demonstrate that upon introducing the transform procedure, the size of the matrix involved in the reconstruction is significantly reduced. As a result, the implementation of the algorithm is significantly accelerated especially for the case when the size of the Jacobian matrix is relatively larger. Meanwhile, the simulation results also demonstrate that our acceleration of the algorithm is achieved under the condition without sacrificing the quality of the reconstruction results.

Cite this paper

Hui Zhang,Si Chen,Jiajun Wang, (2016) The Matrix Transform for Reconstruction on Finite-Element-Based Photoacoustic Tomography. Journal of Computer and Communications,04,54-60. doi: 10.4236/jcc.2016.43008

References

NOTES

^*Corresponding author.