Open Access Library Journal, 2014, 1, 1-8
Published Online June 2014 in OALib. http://www.oalib.com/journal
http://dx.doi.org/10.4236/oalib.1100473
How to cite this paper: Sovizi, M.R. and Madram, A.R. (2014) Investigation of Size Effects on the Al Nanoclusters Physical
Properties via Molecular Dynamics Simulations. Open Access Library Journal, 1: e473.
http://dx.doi.org/10.4236/oalib.1100473
Investigation of Size Effects on the Al
Nanoclusters Physical Properties via
Molecular Dynamics Simulations
Mohammad Reza Sovizi, Ali Reza Madram
Department of Chemistry, Malek Ashtar University of Technology, Tehran, Iran
Received 11 April 2014; revised 21 May 2014; accepted 30 May 2014
Copyright © 2014 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Abstract
Molecular dynamics (MD) simulation has been carried out for study of size effects on physical pro-
perties of Al nanoclusters with different sizes (N = 256, 500, 864, 1372, 2048 and 4000) in the
temperature range 300 K ≤ T ≤ 1200 K for both free and periodic boundary conditions. Energy per
site for periodic and free boundary conditions was calculated for the mentioned sizes and tem-
perature. By increasing size of Al nanocluster, the energy per atom was convergence to that of the
bulk. By use of molecular dynamics some physical properties such as melting point, surface energy,
sublimation energy, thermodynamic limit and pair distribution function have been obtained.
Melting point of bulk state is 875 K which proportional the jump of energy and sharp peak in heat
capacity. Our calculated sublimation energy (ΔHs-calculated = 330 kJ/mol) was in good agreement
with experimental result (ΔHs-experimental = 318 kJ/mol).
Keywords
Molecular Dynamics Simulation, Surface Energy, Al Nanocluster, Physical Properties
1. Introduction
Metal particles with nanometer size containing tens to thousands of atoms; have attracted a great deal of inter-
ests because of a number of their exciting potential applications in catalysis as well as in electronic and optical
nanodevices [1]-[3]. With the decreasing of particle size to nano scale level, they are formed by a limited re-
duced number of atoms and a large fraction of them occupy its surfaces. The strong size effects resulted from
this limitation reduction process may lead to novel and different behaviors. The size and shape are determined
unique properties of metal particles [4].

M. R. Sovizi, A. R. Madram
2
There are many studies which have investigated structural and dynamical behavior of different materials. This
method has been proven to be one of the most powerful tolls to predict and reproduce experimental result
[5]-[7].
Knowledge of their shape and precise structure would be very useful in the determination of their stability and
related properties. Nevertheless, there are few studies to address a thorough energetic and thermal analysis of a
wide variety of nanoparticles.
In recent decades, consolidate solids composed of nanometer size clusters have been attended because they
have unique properties such as electrical, magnetic and thermomechanical properties [8] [9]. In contrast to con-
ventional polycrystalline solids, nanophase materials have a large fraction of atoms in the interfacial region,
which have a dramatic effect on the structure and physical properties of these materials such as surface energy.
The surface energy describe the energetic situation on the surface of solids and the interaction between the co-
hesive and adhesive forces which, in turn, indicate if wetting occurs [10] [11].
Molecula r dy namics simulation for te mperatur e-dependent behavior of solid copper has been studied by Alper
and Politzer [12]. Isothermal isobaric molecular dynamics simulation of water has been done by Amrani et al.
[13]. Dynamic coexistence melting is now well understood in terms of the minimum of the potential energy sur-
face of nano particles [14]-[16]. Ferrando and Baletto [16] were reviewed structural properties of nanoclusters
such as Energetic, thermodynamic and kinetic properties. Calvo et al. [17] were been studied of Al clusters
melting in the size range of 49 ≤ N ≤ 62 by computer simulation and compared with experimental results.
Melting of neutral and singly charged sodium clusters Nan and Nan+ was investigated for several sizes, 8 ≤ n ≤
139 using both Monte Carlo and molecular dynamics simulations with an empirical many-body potential by
Calvo et al. [18]. Up to n = 75, They found that the solid-liquid-like phase change is a multistage process in-
itiated by “pre melting” The equilibrium structure is found to play an important role in the thermodynamics, in
particular when such pre melting features are induced by diffusion processes at the surface. However, larger
sizes n ≥ 93 exhibit preferentially a single process s imilar to th e bulk melting.
Influence of the many-body interactions on the thermodynamics and chaotic dynamics of small atomic clus-
ters has been investigated by Calvo et al. With standard molecular dynamics simulations as well as parallel
tempering Monte Carlo, They calculated the complete heat capacity curves and the variations of the largest
Lyapunov exponent with total energy. They observed that increasing the magnitude or decreasing the range of
the many-body forces leads to an increase of chaos and a decrease in the melting temperature. Decreasing the
range of the many-body interactions also results in a significantly lower latent hea t of melting [19]. Also mole-
cular dynamics simulations were performed to determine the melting point of aluminum nanoparticles of 55 -
1000 atoms by the Streitz and Mintmire [20] [21].
In this letter, we will address the size effects on the thermal characteristics of Al nanoparticles by molecular
dynamics simulations.
2. Molecular Dynamics Simulation
The MD simulations for Al bulk are carried out in a NVT ensemble with a constant number of atoms N, volume
V, and temperature T with the periodic boundary conditions, and for Al nanoclusters are carried out in a NVE
ensemble without any periodic boundary conditions. Temperature is controlled by a Nose-Hoover thermostat
[22] and the equations of motion are integrated using the Verlet Leapfrog algorithm [23] with a time step of
0.001 ps. The system was equilibrated for 400 ps (400,000 time steps), the averages have been computed over
the following 500 ps (500,000 time steps).
In the present study, we have used the DL-POLY-2.20 program [24]. For construction of initial configuration ,
first, a FCC block of Al was constructed from a FCC unit cell by replicatio n in three dimensions with the center
located at (0, 0, 0). The fractional coordinates in the FCC structure are (0, 0, 0), (0.5, 0.5, 0), (0.5, 0, 0.5), and (0,
0.5, 0.5).
In the molecular dynamics simulations, we chose Sutton-Chen (SC) type potentials to describe interatomic
interactions among metal atoms in a nanoparticle. This potential represents the many-body interactions, and
their parameters are optimized to describe the lattice parameter, cohesive energy, bulk modulus, elastic constants,
phonon dispersion, vacancy formation energy, and surface energy, leading to an accurate description of many
properties of metals and their alloys [25]-[28]. For the SC-type force field, the tota l potential energy for a system
of atoms can be written as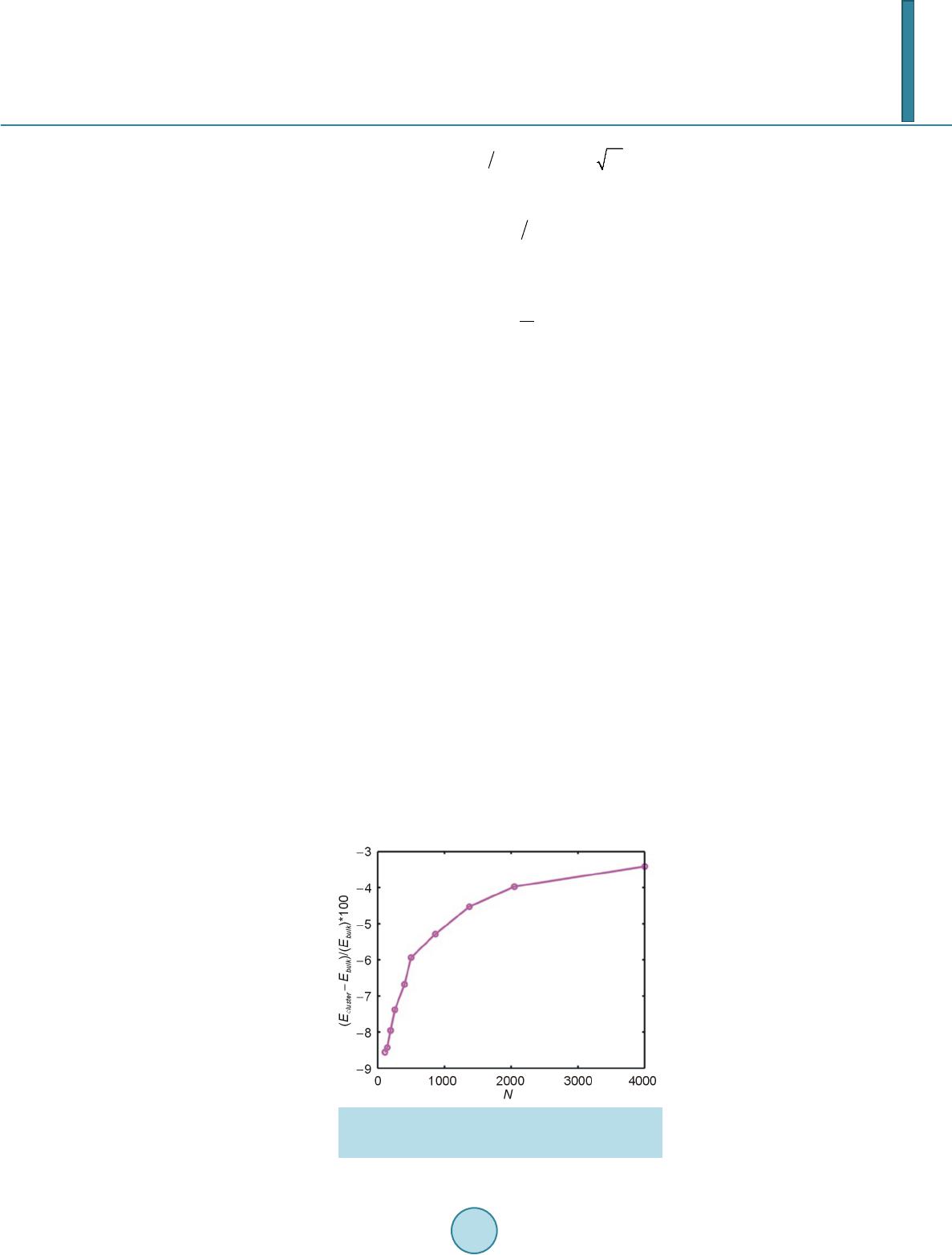

M. R. Sovizi, A. R. Madram
3
()
12
NNN
iij i
ij
i
UVR c ερ
=

= −

∑∑ ∑
(1)
Here
( )
ij
VR
is a pair interaction function defined by the following equation
() ( )
n
ij ij
V RaR=
(2)
Accounting for the repulsion between the i and j atomic cores;
i
ρ
is a local electron density accounting for
cohesion associated with atom i defined by
m
ji ij
a
r
ρ
≠

=


∑
(3)
In Equations (1) and (2),
ij
R
is the distance between atoms i and j, a is a length parameter scaling all spacing
(leading to dimensionless V and ρ); c is a dimensionless parameter scaling the attractive terms; ε sets th e overall
energy scale; n and m are integer parameters such that n > m. Given the exponents (n,m), c is determined by the
equilibrium lattice parameter, and ε is determined by the total cohesive energy. The values of
, , , , anmc ε
for
Al are: 0.033147 (eV), 4.05 (A0), 7.0, 6.0, 16.399, respect i ve ly [23].
3. Result and Discussion
3.1. Thermodynamics Limit
Molecular dynamics simulation has been carried out for Al nanoclusters with different sizes (N = 256, 500, 864,
1372, 2048 and 4000 ) in the temperature range 300 K ≤ T ≤ 1200 K for both free and periodic bound ary condi-
tions. Energy per site for periodic and free boundary conditions is calculated for the mentioned sizes and tem-
perature. By increasing size of Al nanoclusters, the energy per atom convergence to that of the bulk. To obtain
thermodynamic limit, we have calculated the equilibrium configurationally energy per site for the bulk at 300 K.
The percent difference as a function of cluster size is shown in Figure 1.
On the basis of Figure 1, by increasing the cluster size, the magnitude for the difference in configurationally
energy per site of the bulk and nanocluster decreases with N and approaches to zero exponentially. The percent
difference is about 3.5 for N = 4000.
3.2. Surface Energy
The reversible work per unit area to form a new surface of a substance (for instance by cleavage) is defined as
the specific surface free energy (or simply called the surface free energy
γ
), while the r eversible work per unit
area required toelastically stretch a surface is the surface tension,
σ
. The surface free energy constitutes a no-
ticeable contribu tion to the total free energy of a nanoparticle.
Figure 1. Percent difference in energy per site of the
nanoclusters, compared to the bulk value, as a function
of cluster size.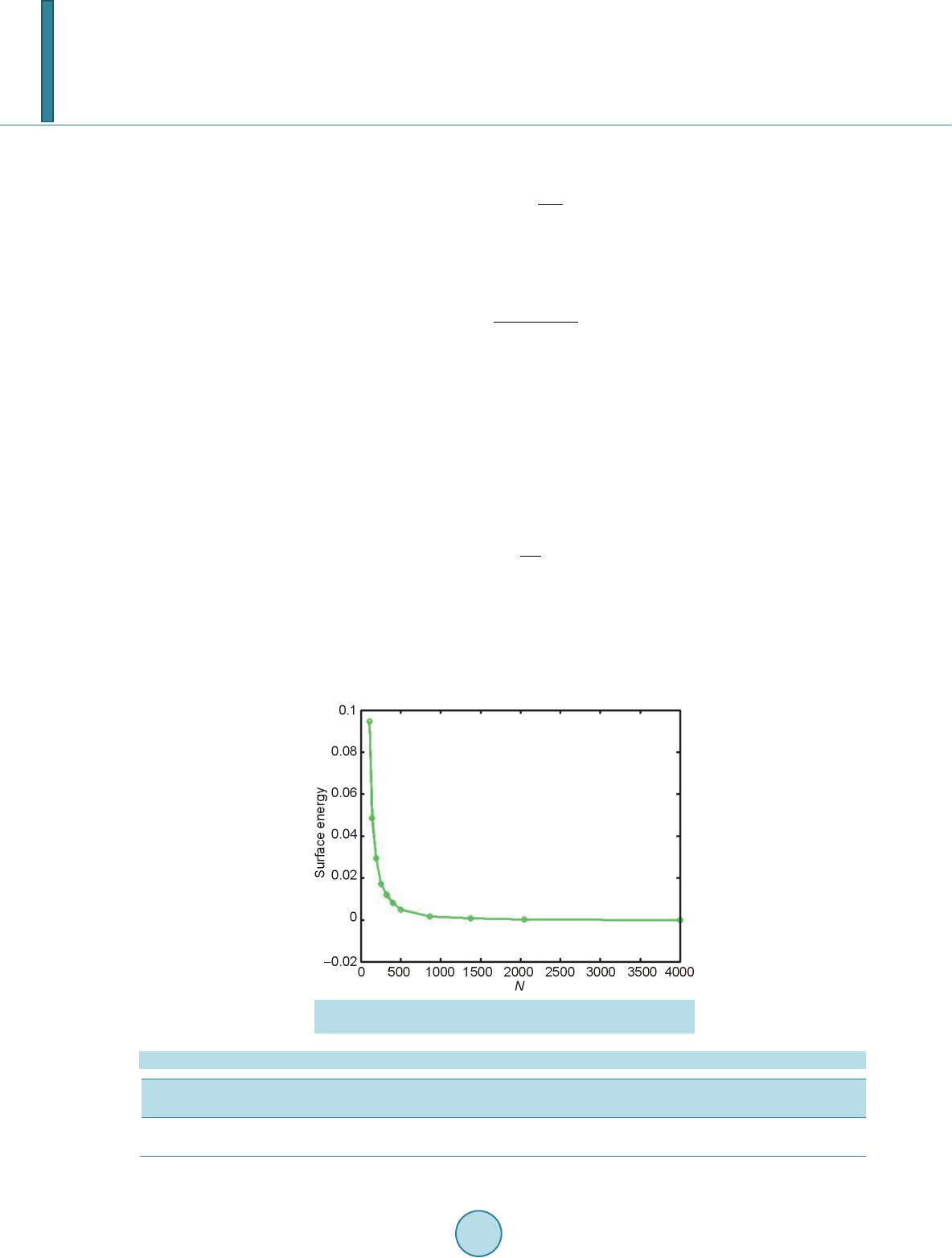

M. R. Sovizi, A. R. Madram
4
For solids, usually the surface tension is not equal to the surface free energy in value. Thus
γ
for a solid
may be computed as
ss
AA
γ
σγ
∂
= +∂
(4)
where
σ
is the surface tension, represents the surface free energy and
s
A
is the surface area. To calculate the
surface free energy, we use the approach given in reference [29].
The surface energy of a cluster may be calculated from
2
4π
cluster bulk
c
EE
R
γ
−
=
(5)
where Ecluster and Ebulk are the potential energies per site of cluster and bulk, respectiv ely, and
c
R
is the cluster
radius at a certain temperature. We have calculated the surface energy (per unit surface area) and cluster radius-
es, at 300 K for diffe re nt s i z es of nan oc l u s t e r 10 8 - 4000, the results are shown in Figure 2.
According to the Figure 2, the surface energy exponentially decreases with the cluster size.
3.2.1. Melting Point of Nanocluster
The configurationally energy per size for the Al nanocluster with different sizes 108, 144, 192, 256, 320, 400,
500, 864, 1372, 2048 and 4000 is calculated at different temperatures 300 K ≤ T ≤ 1200 K. To identify the
melting temperature, we have calculated the specific heat capacity at constant volume C as,
vv
E
CT
∂

=
∂

(6)
A jump in the calculated heat capacity as a function of temperature indicates the melting point. The tempera-
ture range in which the melting occurs for different cluster is summarized in Table 1.
Our result s f or t he melting poi nts of Al nanoc luster shows good agree ments these gi ven in refere nc e [21].
We have taken 3 snapshots for an Al nanocluster with N = 256 at three different temperatures 20 K, 500 K,
and 800 K
Figure 2. Dependence of the surface energy (eV/NA2) to the
cluster size.
Table 1. The range of melting point temperature for the given Al nanoclusters.
Size
(Atom) 108 144 192 256 300 400 500 864 1372 2048 4000
Melting
Point (K) 420 - 470 520 - 560 530 - 560 540 - 570 560 - 590
570 - 590 580 - 600 600 - 620 640 - 650 870 - 872 874 - 875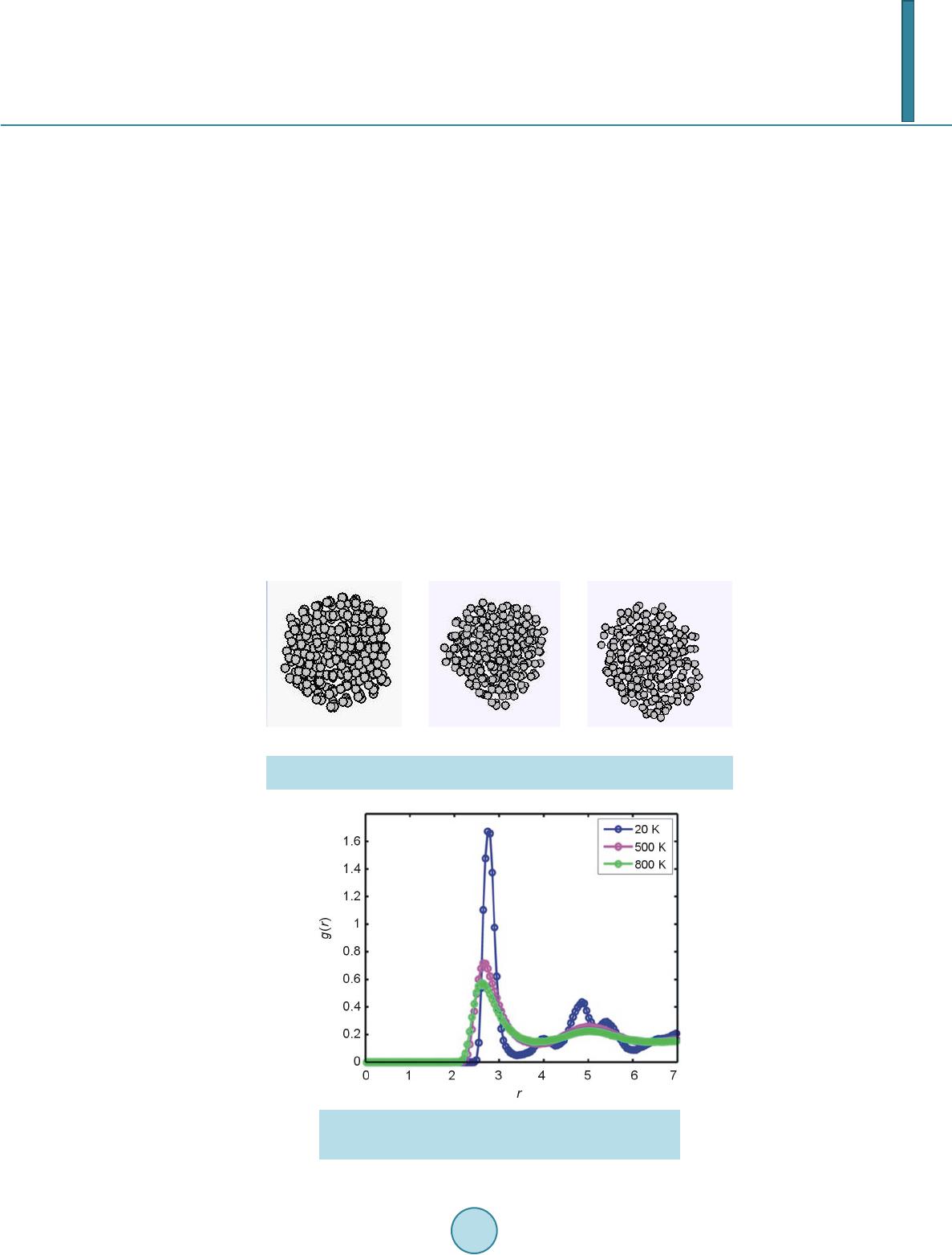

M. R. Sovizi, A. R. Madram
5
According to Figure 3 the Al nanocluster with 256 atoms at the lowest temperature 20 K has an ordered
phase, when temperature increases at 500 K before melting point, the solid of nanocluster becomes disordered,
and finally at 800 K above the melting point the structure of nanocluster is destroyed.
The correlation radial distribution function g(r) is calculated at the three temperatures shown in Figure 4.
On the basis of Figure 4 at the lowest temperature the nanocluster has a very high peak, even at large distance
there are some smaller peaks which indicates the long range order in nanocluster. By increasing temperature the
high peak becomes smaller.
3.2.2. Melting Point of Bulk
Configurationally energy per size of Al bulk using 2048 atom and periodic boundary condition is calculated at
different temperatures within the 300 ≤ T ≤ 1200. The calculated configurationally energy is plotted versus
temperature in Figure 5. On the b asis of Figure 5, ther e is a jump in the configuration energy thorough ly at 875
K.
The calculated heat capacity of the bulk is plotted versus temperature in Figure 6 for 2048 atoms Al in bulk.
The maximum which appears in the specific heat capacity corresponds to the melting point of the bulk.
3.3. Sublimation Energy
Molecular Dynamics simulations have been done at zero pressure; therefore internal energy is equal to enthalpy.
Namely:
H U PVU=+=
(7)
We may assume that Al in gas phase is ideal and then sublimation energy may be given by
(a) (b) (c)
Figure 3. Snapshot of an Al nanocluster with N = 256 at three different temper-
atures: at (a) 20, (b) 500 and (c) 800 K.
Figure 4. Pair correlation function versus distance for the Al-
nanocluster with N = 256 at three different temperatures 20,
500 and 800 K.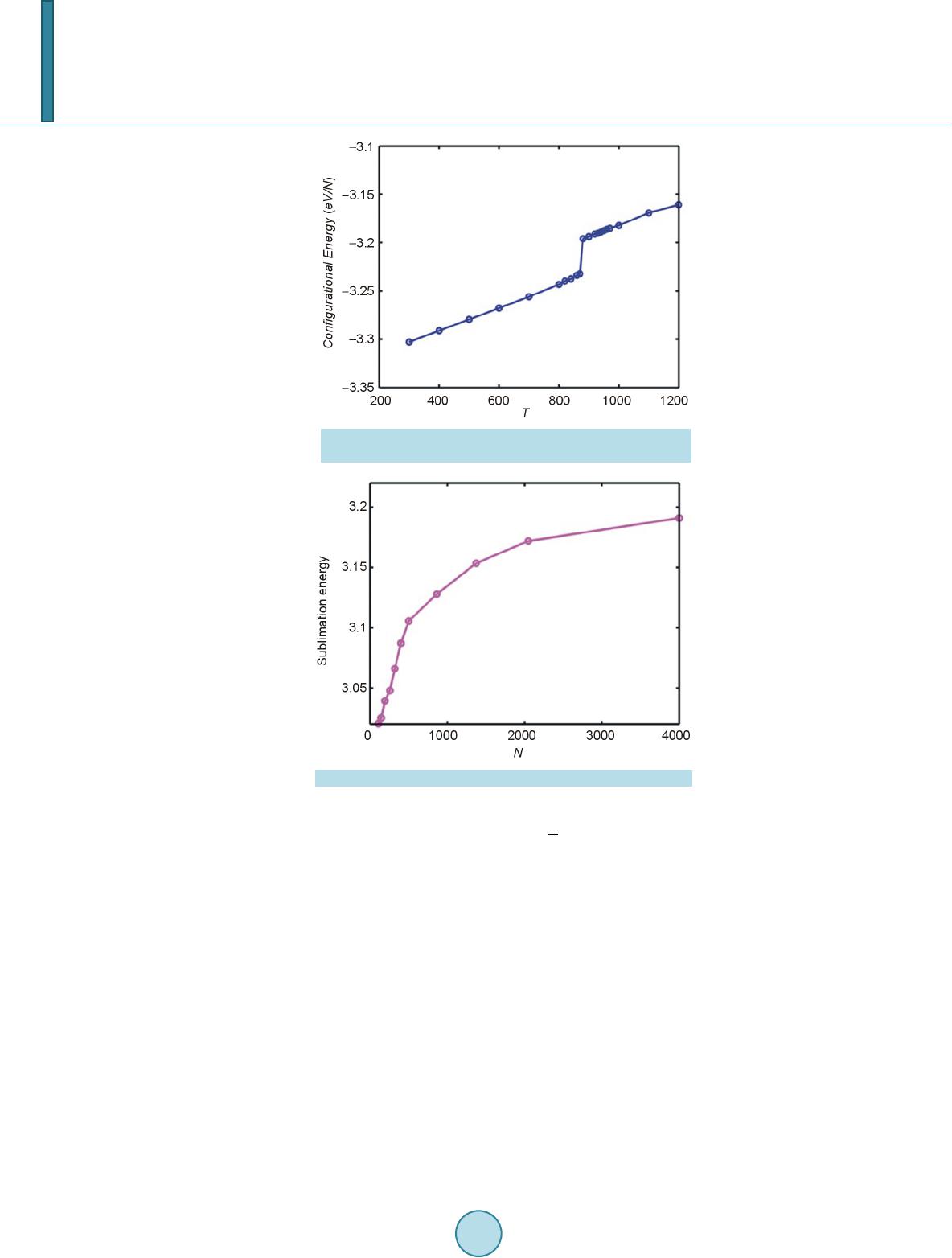

M. R. Sovizi, A. R. Madram
6
Figure 5. Configurationally energy per site for Al bulk versus
temperature.
Figure 6. Heat capacity per size versus temperature for Al bulk.
3
2
s gsBs
HHHNk TU∆=− =−
(8)
Equation (7) is used to calculate for the clusters with different size. The calculated sublimation energy is
shown in Figure 7.
According to Figure 7 the sublimation energy increase with N and asymptotically approach to limit of subli-
mation energy per size is 3.3 eV /N (318 kJ/mol). Experimental value for the sublimation energy was 330 kJ/mol
and it was closed to our result.
4. Conclusion
Molecular dynamics have been used for investigation of thermodynamic properties of Al in nanocluster and bulk
states. Some physical properties such as melting point, surface energy, sublimation energy, thermodynamic limit
and pair distribution function have been obtained. By increasing the size of nanocluster, configuration of energy
approaches to thermodynamic limit. For instance, the relative error from the bulk state for a typical particle con-
sisting 4000 Al atom is roughly 3 percent. Surface free energy decreases exponentially as a function of size and
its values is roughly zero at size of 1372. The main peak of pair distribution function at low temperature (before
melting) is sharp. There are also some other peaks after the main peak which may indicate existence of ordering
in long distance. However, increasing the temperature will result in disappearing and broadening of all the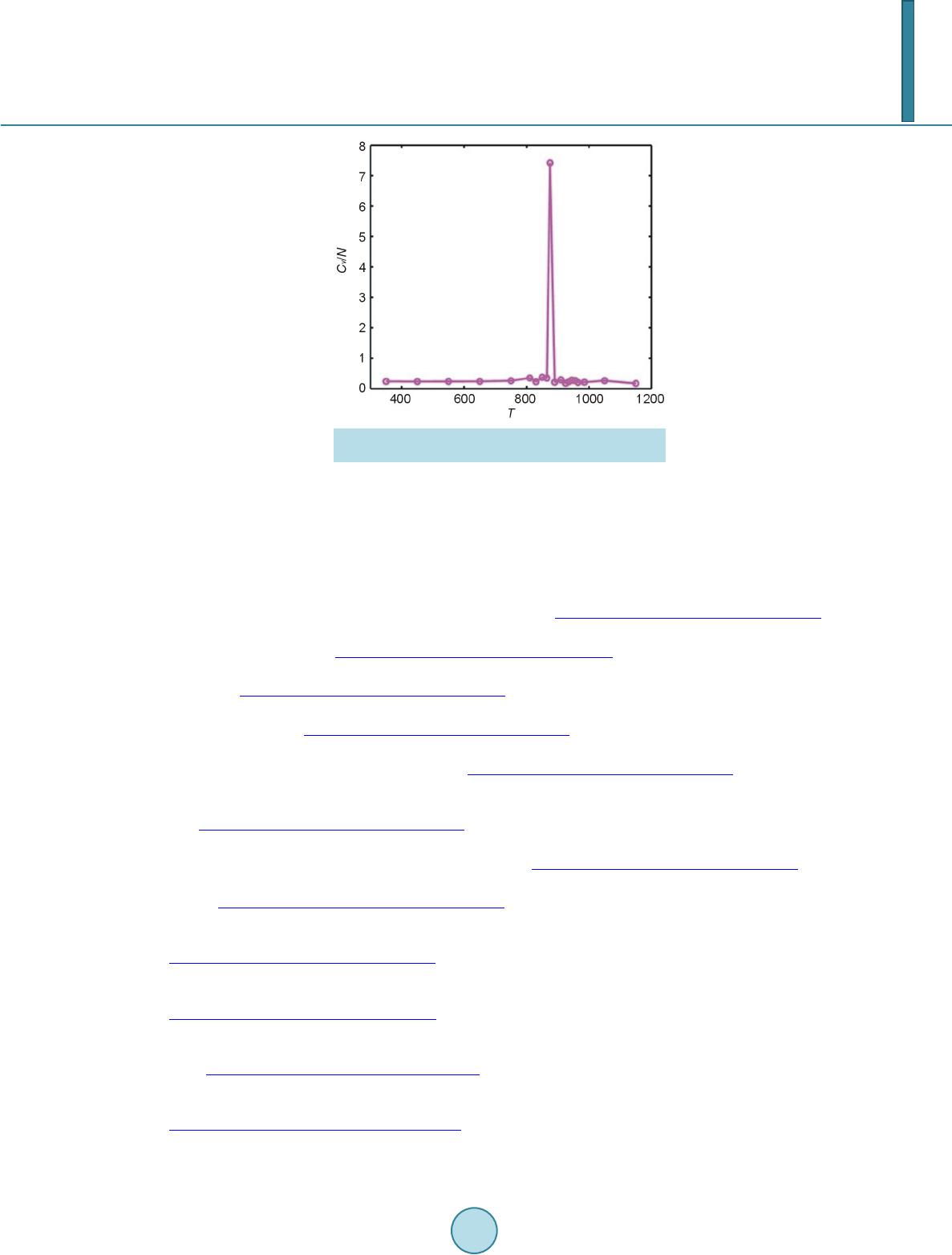

M. R. Sovizi, A. R. Madram
7
Figure 7. Sublimation energy versus size for the Al na-
nocluster.
peaks. Melting point of bulk state is 875 K which proportional the jump of energy and sharp peak in heat capac-
ity. Our calculated sublimation energy is in good agreement with experimental result (ΔHs-calculated = 330 kJ/mol,
ΔHs-experimental = 318 kJ/mol).
References
[1] Zhdanov, V.P., Schwind, M., Zorić, I. and Kasemo, B. (2010) Overheating and Undercooling during Melting and
Crystallization of Metal Nanoparticles. Physica E, 42, 1990-1994. http://dx.doi.org/10.1016/j.physe.2010.03.014
[2] Jensen, P. (1990) Growth of Nanostructures by Cluster Deposition : Expe riments and Simple Models. Reviews of Mod-
ern Physics, 71, 1695-1735. http://dx.doi.org/10.1103/RevModPhys.71.1695
[3] Umeno, A. and Hirakawa, K. (2010) Spectroscopic Analysis of Electromigration at Gold Nanojunctions. Physica E, 42,
2826-2829. http://dx.doi.org/10.1016/j.physe.2009.12.057
[4] Zhdanov, V.P. and Kasemo, B. (2010) Apparent Kinetics of Hydriding and Dehydriding of Metal Nanoparticles. Phy-
sica E, 42, 1482-1486. http://dx.doi.org/10.1016/j.physe.2009.12.002
[5] Rouhi, S. and Ansari, R. (2012) Atomistic Finite El ement Mode l for Axial Buckling and Vibration Analysis of Single-
Layered Graphene Sheets. Physica E, 44, 764-772. http://dx.doi.org/10.1016/j.physe.2011.11.020
[6] Seyyed Fakhrabadi, M.M., Samadzadeh, M., Rastgoo, A., Haeri Yazdi, M. and Mousavi Mashhadi, M. (2012) Vibra-
tional Analysis of Carbon Nanotubes Using Molecular Mechanics and Artificial Neural Network. Physica E, 44, 565-
578. http://dx.doi.org/10.1016/j.physe.2011.10.004
[7] Feng, C. and Jiang, L.Y. (2011) Molecular Dynamics Simulation of Squeeze-Film Damping Effect on Nano Resona-
tors in the Free Molecular Regime. Physica E, 43, 1605-1609. http://dx.doi.org/10.1016/j.physe.2011.05.004
[8] Gleiter, H. (1992) Materials with Ultrafine Microstructures: Retrospective and Perspective. Nanostructured Materials,
1, 1-19. http://dx.doi.org/10.1016/0965-9773(92)90045-Y
[9] Kamenev, B.V., Baribeau, J.-M., Lockwood, D.J. and Tsybeskov, L. (2005) Optical Properties of Stranski-Krastanov
grown Three-Dimensional Si/Si−xGex Nanostructures. Physica E, 26, 174-179.
http://dx.doi.org/10.1016/j.physe.2004.08.047
[10] Kalia, R. K., Nakano, A., Tsuruta, K. and Vashishta, P. (1997) Morphology of Pores and Interfaces and Mechanical
Behavior of Nanocluster-Assembled Silicon Nitride Ceramic. Physical Review Letters , 78, 689-692.
http://dx.doi.org/10.1103/PhysRevLett.78.689
[11] Campbell, T., Kalia, R.K., Nakano, A. and Vashishta, P. (1999) Dynamics of Oxidation of Aluminum Nanoclusters
using Variable Charge Molecular-Dynamics Simulations on Parallel Computers. Physical Review Letters, 82, 4866-
4869. http://dx.doi.org/10.1103/PhysRevLett.82.4866
[12] Alper, H.E. and Politzer, P. (1999) Molecular Dynamics Simulation of the Temperature-Dependent Behavior of Solid
Copper. Journal of Molecular Structure: THEOCHEM, 487,117-125.
http://dx.doi.org/10.1016/S0166-1280(99)00147-5
[13] Amrani, M., Bendeddouch, D., Bormann, D. and Krallafa, A. (2008) Isothermal Isobaric Molecular Dynamics Simula-

M. R. Sovizi, A. R. Madram
8
tion of Water. Journal of Molecular Structure: THEOCHEM, 867, 39-46.
http://dx.doi.org/10.1016/j.theochem.2008.07.017
[14] Wales, D.J. and Berry, R.S. (1994) Coexistence in Finite Systems. Physical Review Letters, 73, 2875-2878.
http://dx.doi.org/10.1103/PhysRevLett.73.2875
[15] Erkoç, Ş. (2000) Stability of Gold Clusters: Molecular-Dynamics Simulatio ns. Physica E, 8, 210-218.
http://dx.doi.org/10.1016/S1386-9477(00)00158-2
[16] Ferrando, R. and Baletto, F. (2005) Structural Properties of Nanoclusters: Energetic, Thermodynamic, and Kinetic
Effects. Reviews of Modern Physics,77, 371-423. http://dx.doi.org/10.1103/RevModPhys.77.371
[17] Calvo, F., Noya, E.G., and Doye, J.P.K. (2006) Theoretical Study of the Melting of Aluminum Clusters. Physical
Review B, 73, 125407-125413. http://dx.doi.org/10.1103/PhysRevB.73.125407
[18] Calvo, F. and Spiegelmann, F. (1999) Geometric Size Effects in the Melting of Sodium Clusters. Physical Review
Letters, 82, 2270-2273. http://dx.doi.org/10.1103/PhysRevLett.82.2270
[19] Calvo, F. and Yurtsever, E. (2000) Many-Body Effects on the Melting and Dynamics of Small Clusters. Physical Re-
view B, 62, 9977-9980. http://dx.doi.org/10.1103/PhysRevB.62.9977
[20] Streitz, F.H. and Mintmire, J.W. (1994) Electrostatic Potentials for Metal-Oxide Surfaces and Interfaces. Physical
Review B, 50, 11996-12003. http://dx.doi.org/10.1103/PhysRevB.50.11996
[21] Alavi, S., Mintmire, J.W. and Thompson, D.L. (2005) Molecular Dynamics Simulations of the Oxidation of Aluminum
Nanoparticles. Journal of Physical Chemistry B, 109, 1518-1523. http://dx.doi.org/10.1021/jp046196x
[22] Nose,S. (1990) Constant-Temperature Molecular Dynamics. Journal of Physics: Condensed Matter, 2, SA115-SA119.
http://dx.doi.org/10.1088/0953-8984/2/S/013
[23] Allen, M.P. and Ti ld esley, D.J. (1997) Computer Simulation of Liquid. Oxford University, New York,
[24] Smith, W. and Todorov, I.T. (2006) A short description of DL_POLY. Molecular Simulation, 32, 935-943.
http://dx.doi.org/10.1080/08927020600939830
[25] Qi, Y. Cagin, T., Johnson, W.L. and Goddard, W.A. (2001) Melting and Crystallization in Ni Nano-Cluste rs: The me-
soscale regime. Journal of Chemical Physics, 115, 385-394. http://dx.doi.org/10.1063/1.1373664
[26] Wen, Y.H., Wu, S.Q., Zhang, J.H. and Zhu, Z.Z. (2008) The Elastic Behavior in Ni Monocrystal: Nonlinear Effects.
Solid State Communications, 146, 253-257. http://dx.doi.org/10.1016/j.ssc.2008.02.020
[27] Sankaranarayanan, S.K.R.S., Bhethanabotla, V.R. and Joseph, B. (2005) Molecular Dynamics Simulation Study of the
Melting of Pd-Pt Nanoclusters. Physica l Review B, 71, 195415-195425.
http://dx.doi.org/10.1103/PhysRevB.71.195415
[28] Vanfleet, R.R. and Mochel, J.M. (19950 Thermodynamics of Melting and Freezing in Small Particles. Surface Science,
341, 40-50. http://dx.doi.org/10.1016/0039-6028(95)00728-8
[29] Wang, L., Zhang, Y., Bian, X. and Chen, Y. (2003) Melting of Cu Nanoclusters by Molecular Dynamics Simulation.
Physics Letters A, 310, 197-202. http://dx.doi.org/10.1016/S0375-9601(03)00263-9