Energy and Power Engineering, 2011, 3, 262-270
doi:10.4236/epe.2011.33033 Published Online July 2011 (http://www.SciRP.org/journal/epe)
Double Multiple Stream Tube Model and Numerical
Analysis of Vertical Axis W ind Turbine
Habtamu Beri, Yingxue Yao
Department of Manufacturing and Automation, Harbin Institute of Technology, Harbin, China
Received April 18, 2011; revised May 2, 2011; accepted May 11, 2011
Abstract
The present paper contributes to the modeling of unsteady flow analysis of vertical axis wind turbine
(VAWT). Double multiple stream tube (DSMT) model was applied for the performance prediction of
straight bladed fixed pitch VAWT using NACA0018 airfoil at low wind speed. A moving mesh technique
was used to investigate two-dimensional unsteady flow around the same VAWT model with NACA0018
airfoil modified to be flexible at 15˚ from the main blade axis of the turbine at the trailing edge located about
70% of the blade chord length using fluent solving Reynolds average Navier-strokes equation. The results
obtained from DMST model and the simulation results were then compared. The result shows that the CFD
simulation with airfoil modified has shown better performance at low tip speed ratios for the modeled tur-
bine.
Keywords: Wind Turbine, Actuator Disk, Momentum Model, Stream Tube, VAWT, CFD
1. Introduction
Over the past decade the wind energy conversion to elec-
tric power has experienced significant progress in the
world. This was made possible by considerable engi-
neering research and development of wind machines
with emphasis on the aerodynamic, structural, and sys-
tems characteristics. The Darrieus rotor VAWT offers a
mechanically and structurally simple method of harness-
ing the energy of the wind. Although first patented in
1931 it has been intensively developed only since 1970,
primarily by the National Research Council of Canada, 2
Sandia National Laboratories, and by others in Europe
[1].
In recent years an increasing demand in decentralized
power plants is observed renewing the interest in Vertical
Axis Wind Turbines (VAWT). The VAWT offers several
advantages when compared to the more conventional
Horizontal-Axis (HAWT) machines. The VAWT is in-
herently Omni-directional and hence obviates the need to
provide a yawing mechanism for keeping the machine
turned into the wind. The transmission and electrical gen-
eration equipment can be located at ground level, thus
tending toward a simpler, lighter structure. The VAWT is
also better able to withstand high winds. In one sense, the
price paid for structural simplicity is aerodynamic com-
plexity: VAWT aerodynamics is inherently unsteady, and
highly nonlinear. However, the relatively recent devel-
opment of several methods capable of predicting steady-
state performance has greatly in-creased our understand-
ing of VAWT aerodynamics [2].
1.1. Power Obtained from Wind Turbine
A simple model, generally attributed to Betz (1926) cited
in [3], can be used to determine the power from an ideal
turbine rotor, the thrust of the wind on the ideal rotor and
the effect of the rotor operation on the local wind field.
This simple model is based on a linear momentum theory.
The analysis assumes a control volume, in which the
control volume boundaries are the surface of a stream
tube and two cross-sections of the stream tube (see Fig-
ure 1). The only flow is across the ends of the stream
tube. The turbine is represented by a uniform “actuator
disk” which creates a discontinuity of pressure in the
stream tube of air flowing through it. Note that this
analysis is not limited to any particular type of wind tur-
bine. This analysis uses the following assumptions:
 Homogenous, incompressible, steady state fluid flow;
 No frictional drag;
 An infinite number of blades;
 Uniform thrust over the disk or rotor area;

H. BERI ET AL.263
Figure 1. Actuator disk model of a wind turbine; V, is air
velocity; 1, 2, 3 and 4 indicate locations.
 A non-rotating wake;
 The static pressure far upstream and far downstream
of the rotor is equal to the undisturbed ambient static
pressure.
Applying the conservation of linear momentum to the
control volume enclosing the whole system, it is possible
to find the net force on the contents of the control vol-
ume. That force is equal and opposite to the thrust, T,
which is the force of the wind on the wind turbine. From
the conservation of linear momentum for a one-dimen-
sional, incompressible, time-invariant flow, the thrust is
equal and opposite to the change in momentum of air
stream:

14
1
TV AVVAV  

4

(1)
where ρ is the air density, A is the cross sectional area, V
is the air velocity and the subscripts indicate values at
numbered cross sections in Figure 1.
For steady state flow, (ρAV)1 = (ρAV)4 =, where
is the mass flow rate.
m
m 
Therefore:

14
TmVV  (2)
The thrust is positive so the velocity behind the rotor,
V4, is less than the free stream velocity, V1. No work is
done on either side of the turbine rotor. Thus the Ber-
noulli function can be used in the two control volumes
on either side of the actuator disk. In the stream tube
upstream of the disk,
2
112
11
22
vpp
2
2
v

  (3)
In the stream tube downstream of the disk,
2
334
11
22
vpp
2
4
v

  (4)
where it is assumed that the far upstream and far down-
stream pressures are equal (p1 = p4) and that the velocity
across the disk remains the same (V2 = V3). The thrust
can also be expressed as the net sum of the forces on
each side of the actuator disc as:

22 3
TAPP

(5)
Solving for “(p2 − p3)” using Equations (3) and (4) and
substituting into (5), it is possible to obtain:

22
21 4
1
2
TAVV  

(6)
Equating the thrust values from (2) and (6) and recog-
nizing that the mass flow rate is A2V2,
14
22
VV
V
 (7)
Thus, the wind velocity at the rotor plane, using this
simple model, is the average of the upstream and down-
stream wind speeds. If one defines the axial induction
factor “a”, as the fractional decrease in wind velocity
between the free stream and the rotor plane, then
12
1
VV
aV

 (8)

21
1VV a


 (9)


41
12VV a (10)
From (6), (9) and (10), the axial thrust on the disk is:

2
1
141
2
TAVaa  



 (11)
The thrust on a wind turbine can be characterized by a
non-dimensional thrust coefficient as:
2
Thrust force
1dynamic force
2
T
T
C
AV 
 (12)
From (12), the thrust coefficient for an ideal wind tur-
bine is equal to 4a(l − a).
1.2. General Mathematical Expressions for
Aerodynamics Analysis of Straight Bladed
Darrieus VAWT
Straight bladed darrieus type VAWT is known for its
simplest type of wind turbine. However, its aerodynamic
analysis is quite complex. Flow velocities in the up-
stream and downstream sides of the Darrieus-type
VAWTs are not constant. The general mathematical ex-
pressions at a specific location of the blade is described
below.
From Figure 2 the relative velocity component (VR)
can be obtained from the cordial velocity component and
the normal velocity component as follows

H. BERI ET AL. 264
Figure 2. Airfoil velocity and force diagram.

22
sin
Ra a
VV VcosR   (13)
where Va is the axial flow velocity (i.e. induced velocity)
through the rotor, ω is the rotational velocity, R is the
radius of the turbine, and θ is the azimuth angle.
Normalizing the relative velocity using free stream
wind velocity one can obtain:
2
sin cos
aa RVV
VR
VVV V


 




2



(14)
Referring back to (9) and substituting V2 with Va and
V1 with V∞, Equation (14) can be re-written as:




2
1sin 1cos
R
Vaa
V
2



  (15)
where “a” is induction factor and “λ” is tip speed ratio of
the turbine.
Referring Figure 2, angle of attack can be expressed
as:
sin
tan cos
a
a
V
VR




 (16)
Non-dimensionalizing the equation,
sin
tan
cos
a
a
V
V
VR
VV








(17)


11sin
tan 1cos
a
a












(18)
The normal and tangential coefficients can be ex-
pressed as
cos sin
nL D
CC C



 (19)
sin cos
tL D
CC C



 (20)
where CL lift coefficient and CD drag coefficient for an-
gle of attack α
The instantaneous thrust force (Ti) on one single airfoil
at certain θ is
 
2
1cos sin
2
iR tn
TVhcC C

   (21)
where “h” is blade height and “c” blade chord length
The instantaneous torque (Qi) on one single airfoil at
certain θ is

2
1
2
iR
QVhcC  t R (22)
1.3. Computational Models for Darrieus-Type
Straight-Bladed VAWT
In the past, several mathematical models, based on sev-
eral theories, were prescribed for the performance pre-
diction and design of Darrieus-type VAWTs by different
researchers. According to literature survey, the most
studied and validated models can be broadly classified
into three categories (1) Momentum model, (2) Vortex
model and (3) Cascade model. For the purpose of this
paper momentum model is chosen to predict the per-
formance of VAWT as it is fast and provide reasonably
accurate prediction of steady state average turbine out-
put.
Momentum models: the first application of momen-
tum theory to the modelling of VAWTs is attributed to
Templin [4]. He used a single stream tube encompassing
the entire turbine within which the momentum balance
was calculated. The flow velocity within the stream tube
was assumed to be uniform. Wilson and Lissaman [5]
assumed a sinusoidal variation in inflow velocity across
the width of the turbine to account for non-uniform flow.
In order to account for this effect more fully, Strickland
[6] extended the model so that the flow through the tur-
bine is divided into multiple independent stream tubes as
shown in Figure 3. The momentum balance is carried
out separately for each stream tube, allowing an arbitrary
variation in inflow.
A single blade passes each stream tube twice per
revolution in the upstream and downsteam. The instan-
taneous thrust force on one single blade is given in
Equation (21). The time averaged thrust force acting in a
stream tube by “N” blades and twice per revolution can
be expressed as
instantaneous thrust2
π
a
TN
 

 (23)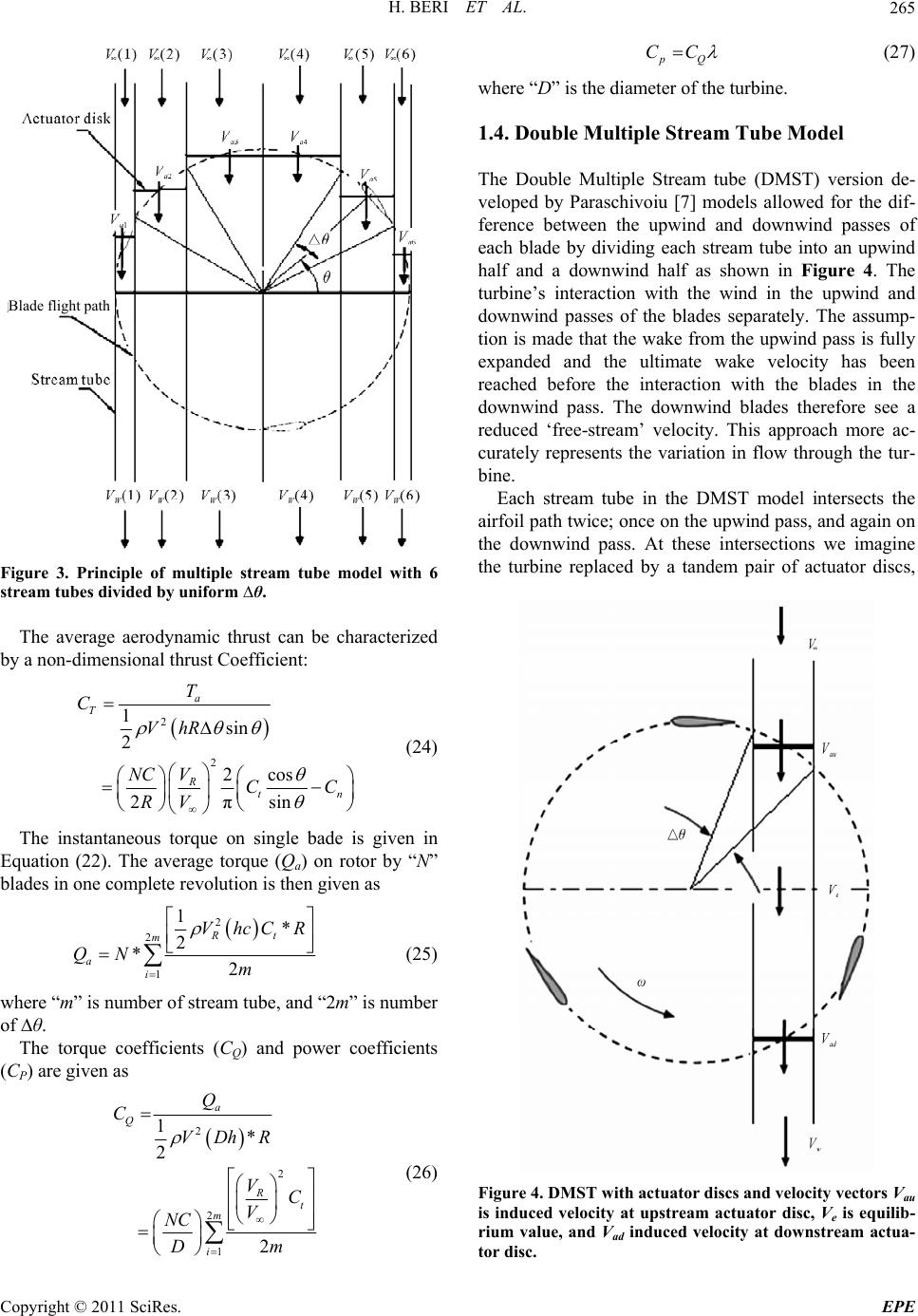

H. BERI ET AL.265
Blade flight path
Figure 3. Principle of multiple stream tube model with 6
stream tubes divided by uniform ∆θ.
The average aerodynamic thrust can be characterized
by a non-dimensional thrust Coefficient:

2
2
1sin
2
2cos
2πsin
a
T
R
tn
T
C
VhR
V NC CC
RV







 


 
 




(24)
The instantaneous torque on single bade is given in
Equation (22). The average torque (Qa) on rotor by “N”
blades in one complete revolution is then given as

2
2
1
1*
2
*2
Rt
m
a
i
VhcCR
QN m






(25)
where “m” is number of stream tube, and “2m” is number
of ∆θ.
The torque coefficients (CQ) and power coefficients
(CP) are given as

2
2
2
1
1*
2
2
a
Q
R
t
m
i
Q
C
VDhR
VC
V
NC
Dm



















(26)
pQ
CC


(27)
where “D” is the diameter of the turbine.
1.4. Double Multiple Stream Tube Model
The Double Multiple Stream tube (DMST) version de-
veloped by Paraschivoiu [7] models allowed for the dif-
ference between the upwind and downwind passes of
each blade by dividing each stream tube into an upwind
half and a downwind half as shown in Figure 4. The
turbine’s interaction with the wind in the upwind and
downwind passes of the blades separately. The assump-
tion is made that the wake from the upwind pass is fully
expanded and the ultimate wake velocity has been
reached before the interaction with the blades in the
downwind pass. The downwind blades therefore see a
reduced ‘free-stream’ velocity. This approach more ac-
curately represents the variation in flow through the tur-
bine.
Each stream tube in the DMST model intersects the
airfoil path twice; once on the upwind pass, and again on
the downwind pass. At these intersections we imagine
the turbine replaced by a tandem pair of actuator discs,
Figure 4. DMST with actuator discs and velocity vectors Vau
is induced velocity at upstream actuator disc, Ve is equilib-
rium value, and Vad induced velocity at downstream actua-
tor disc.

H. BERI ET AL. 266
upon which the flow may exert force. The DMST model
simultaneously solves two equations for the stream-wise
force at the actuator disk; one obtained by conservation
of momentum and other based on the aerodynamic coef-
ficients of the airfoil (lift and drag) and the local wind
velocity. These equations are solved twice; for the up-
wind and for the downwind part of the rotor.
Now according to the actuator disk theory shown in
(7) above the induced velocity (Vau) on the upstream
wind will be the average of the air velocity at far up-
stream (V∞) and the air velocity at downstream equilib-
rium (Ve). Thus

1 or, 2
2
auee au
VVVVV

 V

(28)
The present paper attempts to evaluate the perform-
ance of fixed pitch vertical axis with three blades using
double multiple stream tube (DMST) model and 2D un-
steady flow analysis using CFD. The conventional air-
foils used for Darrieus VAWTs were NACA0012,
NACA0015 & NACA0018. These blades are of sym-
metrical geometry with minimum or negative torque
generations at lower TSRs. Among these blades profile
NACA0018 was chosen for the analysis. This is due to
the availability of experimental data’s for comparison.
The airfoil chosen was modified to vary at the trailing
edge from the original geometry. This makes the turbine
blade to have two parts with fixed part and flexible.
The assumption for the modification of the airfoil was
to increase the lift forces for the performance of the tur-
bine at lower tip speed ratio. The flexible part assumed to
case variation of the wind velocity that passes on the top
and lower surface of the airfoil. This causes pressure
differences on airfoil so that lift force can be generated
for better performance of turbine at lower tip speed ratio.
Once the turbine passed the negative torque generation,
the flexible part assumed to take the same orientation
with the main airfoil for operation at higher tip speed
ratios like the conventional symmetrical airfoil geometry.
In the analysis, the conventional NACA0018 symmet-
rical airfoil was used for the analysis of multiple stram-
tube (DMST) model. The same NACA0018 symmetrical
airfoil was made to be divided into two parts at about
70% of the cord length as shown in Figure 5 for its 2D
unsteady flow analysis using commercial CFD software
based on Reynolds averaged Navier-stokes (RANS)
equation using moving mesh technique. The trailing edge
Figure 5. Modified geometry of NACA0018 airfoil.
axis inclination was set to 15˚ from the main blade axis.
2. Methodology
2.1. CFD Analysis
For the VAWT analysis, the modified airfoil was set to
0.2 m chord length with radius equal to 2 m. Gambit
modeling software was used to create 2D model of the
turbine. The model and mesh generated were then read
into the commercial CFD code fluent for numerical iter-
ate solution. The RANS equations were solved using the
green-gauss cell based gradient option and the sliding
mesh method was used to rotate the turbine blades. The
RNG k-epsilon model was adapted for the turbulence
closure.
The boundary conditions are shown in Figure 6. The
inlet was defined as a velocity inlet, which has constant
inflow velocity, while the out let was set as a pressure
out let, keeping the pressure constant. The no slip shear
condition was applied on the turbine blades, which set
the relative velocity of the blades to zero. The flow con-
dition used for the analysis is shown in Table 1.
Figure 6. Boundary conditions.
Table 1. Flow conditions.
TSR(λ) Velocity m/s Turbine ang.vel. (rad/s)
0.25 4 0.5
0.5
0.75
4
4
1
1.5
1 4 2
1.5 4 3
2 4 4
3 4 6
3.5 4 7
4 4 8
5 4 10

H. BERI ET AL.267
2.2. DMST Analysis
Similarly, For the VAWT analysis using DMST, the
normal NACA0018 airfoil was set to 0.2m chord length
and the turbine radius was set to 2m. The wind velocity
used in the analysis is 4 (m/s) and the tip speed ratios (λ)
are 0.5, 1, 1.5, 2, 3, 4, 5, and 6. The total number of
stream tube used for the analysis is 12 with ∆θ = 15˚.
The iterative procedure used in the DMST analysis is
shown in Figure 7. A spreadsheet is used for easy man-
agement of the data. The mesh generated near the rotor
for the numerical analysis is shown in Figure 8.
The induction factor “a” was calculated for all of the
stream tube twice, one for half upstream of the turbine
and the other half downstream of the turbine. The lift and
drag coefficients for NACA0018 section used are the
data of Sheldal and klimas [8], corrected by Lazauskas
(2002). Since the momentum equation in (12) is not ap-
plicable beyond induction factor of “0.5” the Glauert
empirical formula is used to calculate the thrust coeffi-
cient for 0.4 < a < 1.0.
3. Results and Discussions
Figure 9 shows the coefficient of power (Cp) compari-
son between computational fluid dynamics (CFD) and
double multiple stream tube (MDST) model. The coeffi-
cient of power for the modified airfoils was generated by
combining the performance of turbine trailing edge in-
clined at 15˚ for TSR 0.1 to 1 and without inclination of
the trailing edge for TSR greater than 1. The Cp was
obtained from the ratio of the modeled turbine power to
the available wind power in the air.
DMST Cp curve shows that the turbine generates
negative torque for lower tip speed ratios less than about
2.6. Whereas the CFD analysis for the modified airfoil
shows, positive torque at low tip speed ratios.
Figure 10 shows the coefficient of moment (Cm) of
the simulated model at low tip speed ratio. The Cm val-
ues were obtained from the average moment of the three
airfoils modeled through CFD computational analysis for
the modified airfoil for tip speed ratios 0.1, 0.25, 0.75
and 1. As can be seen, Cm near zero is higher and seems
to reduce up to TSR = 0.5 and then starts to rise.
Figure 11 shows simulated torque values for the mod-
eled NACA0018 modified airfoil at lower TSR. It shows
the torque values at different azimuth angle in N-m for
complete revolution of TSRs 0.1, 0.25, 0.5, 0.75 and 1.
The torque values were obtained from coefficient mo-
ment (Cm) of the modeled airfoil, air density, turbine
area, free stream velocity chosen and the radius of the
turbine modeled. The graph shows that the average
torque values at each of the TSR simulated are positive.
Assumeavalueforinductionfactora
CalculateNormalizedvelocity,attackangle,lift,
drag,no r ma landtangentialcoefficients
Calculatethrustcoefficientderivedfrom
aerodynamicsforces
Calculatethrustcoefficientderivedfromtheory
ofactuatordisc(momentumloss)
Compareaerody na m ic thrustcoefficientwith 
momentumloss 
Arethethrust
coefficientsthesame?
Acceptvaluesofaforthestreamtube
No
Yes
Figure 7. Iterative procedure used to calculate the flow ve-
locity.
Figure 8. Mesh near the rotor.
Figure 12 shows the steady state torque values at TSR
0 for different wind speeds at three different orientations
of the blades. The blade orientations were taken at three
different azimuth angles of 0˚, 45˚ and 90˚. This helps to
show the performance of the turbine at its steady state.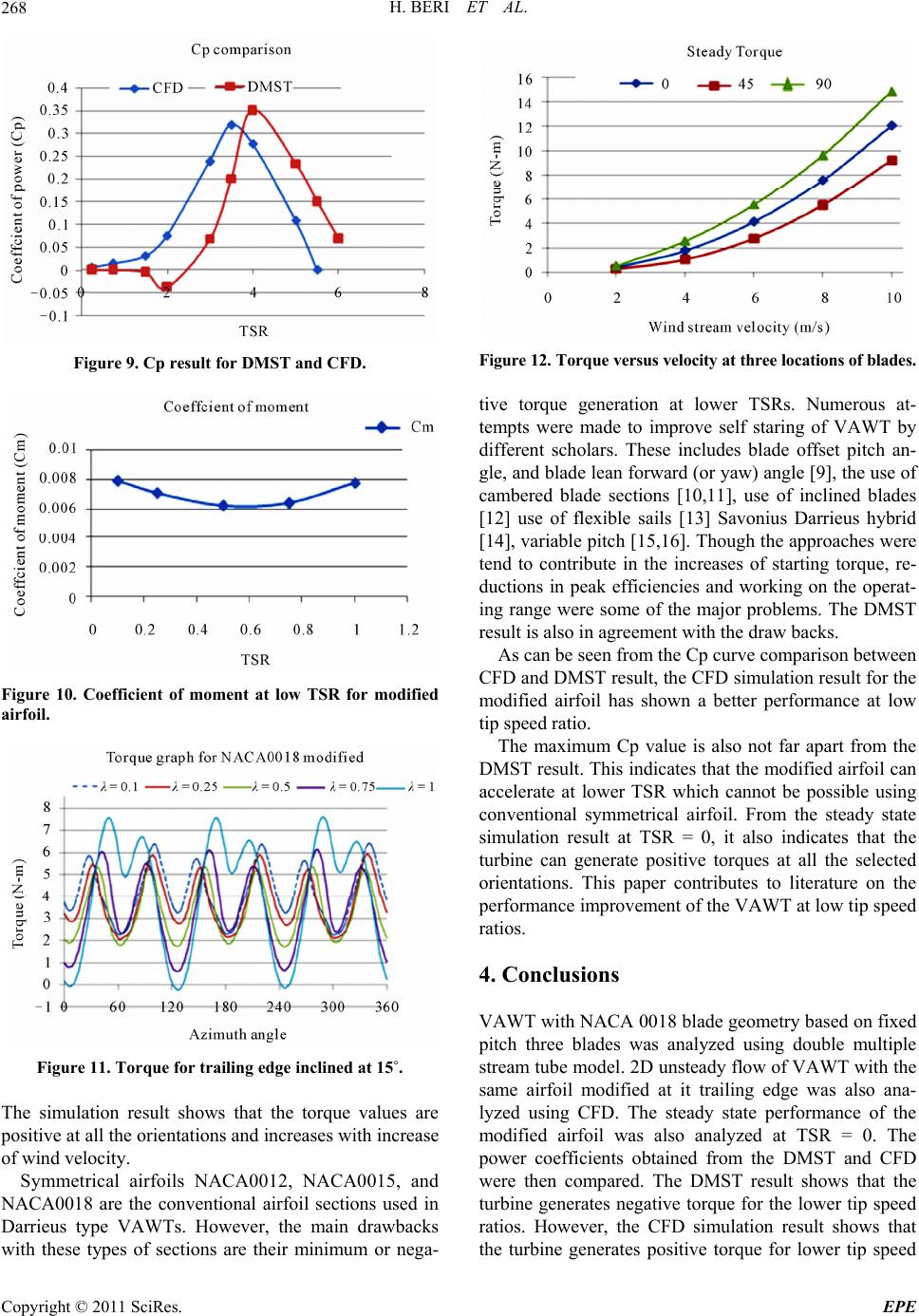

H. BERI ET AL. 268
Figure 9. Cp result for DMST and CFD.
Figure 10. Coefficient of moment at low TSR for modified
airfoil.
Figure 11. Torque for trailing edge inclined at 15˚.
The simulation result shows that the torque values are
positive at all the orientations and increases with increase
of wind velocity.
Symmetrical airfoils NACA0012, NACA0015, and
NACA0018 are the conventional airfoil sections used in
Darrieus type VAWTs. However, the main drawbacks
with these types of sections are their minimum or nega-
Figure 12. Torque versus velocity at three locations of blades.
tive torque generation at lower TSRs. Numerous at-
tempts were made to improve self staring of VAWT by
different scholars. These includes blade offset pitch an-
gle, and blade lean forward (or yaw) angle [9], the use of
cambered blade sections [10,11], use of inclined blades
[12] use of flexible sails [13] Savonius Darrieus hybrid
[14], variable pitch [15,16]. Though the approaches were
tend to contribute in the increases of starting torque, re-
ductions in peak efficiencies and working on the operat-
ing range were some of the major problems. The DMST
result is also in agreement with the draw backs.
As can be seen from the Cp curve comparison between
CFD and DMST result, the CFD simulation result for the
modified airfoil has shown a better performance at low
tip speed ratio.
The maximum Cp value is also not far apart from the
DMST result. This indicates that the modified airfoil can
accelerate at lower TSR which cannot be possible using
conventional symmetrical airfoil. From the steady state
simulation result at TSR = 0, it also indicates that the
turbine can generate positive torques at all the selected
orientations. This paper contributes to literature on the
performance improvement of the VAWT at low tip speed
ratios.
4. Conclusions
VAWT with NACA 0018 blade geometry based on fixed
pitch three blades was analyzed using double multiple
stream tube model. 2D unsteady flow of VAWT with the
same airfoil modified at it trailing edge was also ana-
lyzed using CFD. The steady state performance of the
modified airfoil was also analyzed at TSR = 0. The
power coefficients obtained from the DMST and CFD
were then compared. The DMST result shows that the
turbine generates negative torque for the lower tip speed
ratios. However, the CFD simulation result shows that
the turbine generates positive torque for lower tip speed

H. BERI ET AL. 269
ratios. The steady state performance at three different
orientations also indicates positive torque. The maximum
power coefficients show that both are in the normal
range of turbine performance.
5. References
[1] I. Paraschivoiu, “Double-Multiple Stream Tube Model
for Studying Vertical-Axis Wind Turbines,” Journal of
Propulsion and Power, Vol. 4, No. 4, 1988, p. 370.
doi:10.2514/3.23076
[2] G. F. Homicz, “Numerical Simulation of VAWT. Stochas-
tic Aerodynamic Loads Produced by Atmospheric Turbu-
lence: VAWT-SAL Code,” Technical Report SAND91-
1124, Sandia National Laboratories, Albuquerque, 1991.
[3] J. F. Manwell, J. G. McGowan and A. L. Rogers, “Wind
Energy Explained: Theory Design and Application,” John
Wiley & Sons, Hoboken, 2002.
[4] R. Templin, “Aerodynamic Performance Theory for the
NRC Vertical-Axis Wind Turbine,” National Aeronauti-
cal Establishment Laboratory Technical Report LTR-
LA-160, National Research Council, Canada, 1974.
[5] R. Wilson and P. Lissaman, “Applied Aerodynamics of
Wind Powered Machines,” Technical Report NSF-RA-
N-74-113, Oregon State University, Corvallis, 1974.
[6] J. Strickland, “The Darrieus Turbine: A Performance
Prediction Model Using Multiple Stream Tubes,” Tech-
nical Report SAND75-041, Sandia National Laboratories,
Albuquerque, 1975.
[7] I. Paraschivoiu, “Aerodynamic Loads and Performance of
the Darrieus Rotor,” Journal of Energy, Vol. 6, No. 6,
1981, pp. 406-421. doi:10.2514/3.62621
[8] R. E. Sheldal and P. C. Klimas, “Aerodynamic Charac-
teristics of Seven Airfoil Sections through 180 Degrees
Angle of Attack for Use in Aerodynamic Analysis of
Vertical Axis Wind Turbines,” Sandia National Labora-
tories, Albuquerque, 1981.
[9] L. Lazauskas, “Three Pitch Control Systems for Vertical
Axis Wind Turbines Compared,” Wind Engineering, Vol.
16, 1992, pp. 269-269.
[10] V. G. Dereng, “Fixed Geometry Self Starting Transverse
Axis Wind Turbine,” US Patent No. 4264279, 1981.
[11] H. Beri and Y. Yao, “Effect of Camber Airfoil on Self
Starting of Vertical Axis Wind Turbine,” Journal of En-
vironmental Science and Technology, Vol. 4, No. 3, 2011,
pp. 302-312. doi:10.3923/jest.2011.302.312
[12] J. R .Barker, “Features to Aid or Enable Self Starting of
Fixed Pitch Low Solidity Vertical Axis Wind Turbines,”
Journal of Wind Engineering and Industrial Aerodynam-
ics, Vol. 15, No. 1-3, 1983, pp. 369-380.
doi:10.1016/0167-6105(83)90206-4
[13] B. Hurley, “A Novel Vertical Axis Sail Rotor,” Proceed-
ings of 1st Wind Energy Workshop, London, 19-20 April
1979, pp. 40-47.
[14] T. Wakui, Y. Tanzawa, T. Hashizume and T. Nagao,
“|Hybrid Configuration of Darrieus and Savonius Rotors
for Stand-Alone Wind Turbine-Generator Systems,”
Electrical Engineering in Japan, Vol. 150, No. 4, 2005,
pp. 13-22. doi:10.1002/eej.20071
[15] H. M. Dreess, “Self-Starting Windmill Energy Conver-
sion System,” US Patent No. 4180367, 1979.
[16] L. Liljegren, “Vertical Axis Wind Turbine,” US Patent
No. 4430044, 1984.

H. BERI ET AL. 270
Abbreviations and Acronyms
A projected frontal area of turbine
a induction factor
C blade chord length
CFD computational fluid dynamics
CD lade drag coefficient
CL lade lift coefficient
Cm coefficient of moment
Cn normal force coefficient
CQ torque coefficient
Ct tangential force coefficient
CT thrust coefficient
D turbine diameter
DMST double multiple stream tube
h height of turbine
m number of stream tube
m
 mass flow rate
N number of blade
p static pressure
P∞ atmospheric pressure
Qi instantaneous torque
Qa average torque
R turbine radius
RANS Reynolds average Navier -strokes
T thrust force
Ta average thrust force
Ti instantaneous thrust force
TSR tip speed ratio
V air velocity along freestream velocity direction
Va induced velocity
Vad induced velocity in the downstream side
Vau induced velocity in the upstream side
Ve equilibrium value wind velocity
VR relative flow velocity
Vw wake velocity in downstream side
V∞ stream wind velocity
VAWT vertical axis wind turbine
α blade angle of attack
θ azimuth angle
∆θ stream tube angle division value
λ tip speed ratio = Rω/V∞
ρ fluid density
ω angular velocity of turbine in rad/s