Paper Menu >>
Journal Menu >>
 Energy and Power En gi neering, 2011, 3, 227-237 doi:10.4236/epe.2011.33029 Published Online July 2011 (http://www.SciRP.org/journal/epe) Copyright © 2011 SciRes. EPE Theoretical and Numerical Analysis of the Mechanical Erosion in Steam Turbine Blades. Part I Fernando Rueda Martínez, Miguel Toledo Velázquez, Florencio Sánchez Silva, Aldo Antonio Rueda Martínez, Samuel Alcántara Montes, Oliver Marciel Huerta Chávez Applied Thermal and Hydraulic Engineering Laboratory, Lindavista, Mexico E-mail: mtv49@yahoo.com Received April 1, 2011; revised May 2, 2011; accepted May 13, 2011 Abstract The methodology of calculation of the velocity distribution for the stream frictionless and the drops in the flow line, on the basis of the frictionless, two-dimensional, stationary, transonic and homogenous flow is es- tablished. The knowledge of conditions that govern the low pressure section of steam turbines in the last stage to have an approximate movement of the droplets in the blade cascades and the accumulation of drop- lets on the stator blades, flowing through the steam, is presented. This study is used for developing a code in Fortran about the velocity distribution in the output of stator blades that have flow conditions of wet steam, in order to understand the causes that originate the erosion on the blades of the last stages in the low pressure section of steam turbines. Keywords: Steam Turbine, Drop Distribution, Erosion Stator-Rotor Blade, Transonic Flow 1. Introduction Nucleation is the energy necessary to form a stable droplet, also named thermodynamic barrier of germina- tion. In a microscopic level, phase fluctuations occur as random events due to the thermal vibration of atoms (collisions). In terms of classical nucleation theory, the spontaneous fluctuations lead to the formation of small embryonic droplet that can grow beyond some critical radius, being possible to overcome this barrier and to hold its spontaneous growth; that is, it can only survive and grow up if there is a reduction in free energy [1]. However, if the energy barrier to spontaneous growth is large and the droplet cannot achieve its critical size, it remains unstable and possibly will evaporate. As a result of this energy barrier, the system can exist in a metasta- ble state with unfavorably high supersaturation levels being maintained in the gas phase. The existence of wa- ter droplets formation presents practical difficulty con- cerning the behavior of steam in turbines. The tempera- ture and pressure gradients are such that droplets might nucleate with undesirable effects on the performance of the machine, including the erosion of turbine blades due to the repeated impact on them. In the case of condensed phases, the principal idea is that exist a bottleneck in the transformation, which is passed through only by frag- ments, or molecular clusters, of the new phase. The clus- ter is a group of individual units mutually interrelated in all directions: vertical, horizontal, etc., that establishes a functional interdependence for the development of its processes. The bottleneck is narrowest when the clusters reach a so-called critical size. The capillarity approxima- tion is employed, whereby the critical cluster, however small, is considered as a scaled-down macroscopic drop- let of the condensed phase. Until recently, the moisture nucleation in turbines has been assumed as a homogene- ous process with the effects of steam impurities being negligible, as in this case of study. Generally, depending of the conditions of work of the turbine, in the two or third rotor stage is found heteroge- neous nucleation transition (molecules nucleate onto surfaces). In the fourth stator stage can creates the pri- mary nucleation toward the shroud. As flow expansion continues into the final stage, significant supercooling is again possible, leading to further secondary homogene- ous nucleation along the final rotor stage. Finally, smaller droplets generated along the third rotor inlet and outlet stage can be collected on blades and re-entrained as secondary droplets into the flow at the trailing edges of rotating components [2]. Importantly, the droplets generated along the inlet of third rotor blades through rotor fifth stage remain quite small, can be adequately 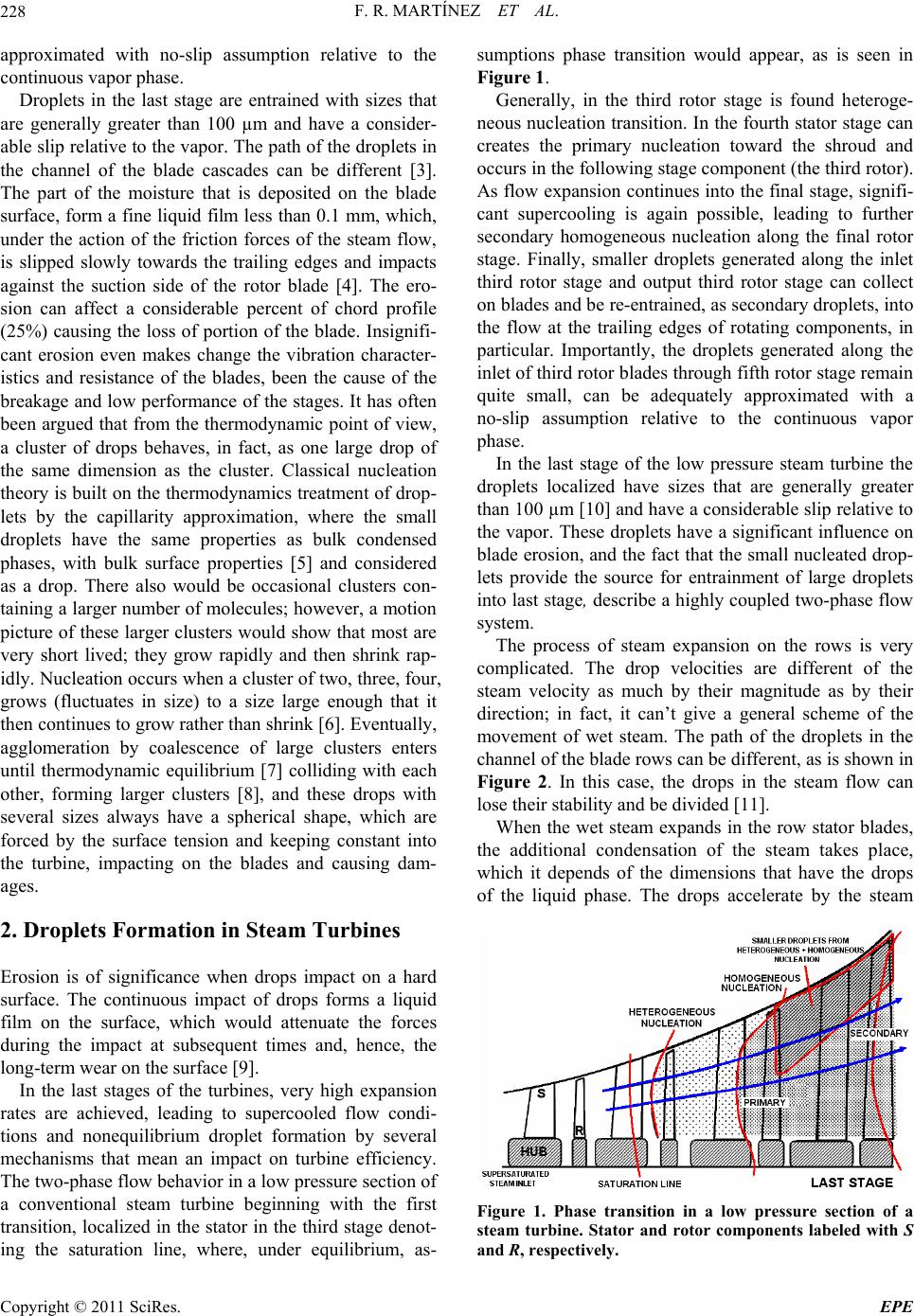 F. R. MARTÍNEZ ET AL. 228 approximated with no-slip assumption relative to the continuous vapor phase. Droplets in the last stage are entrained with sizes that are generally greater than 100 µm and have a consider- able slip relative to the vapor. The path of the droplets in the channel of the blade cascades can be different [3]. The part of the moisture that is deposited on the blade surface, form a fine liquid film less than 0.1 mm, which, under the action of the friction forces of the steam flow, is slipped slowly towards the trailing edges and impacts against the suction side of the rotor blade [4]. The ero- sion can affect a considerable percent of chord profile (25%) causing the loss of portion of the blade. Insignifi- cant erosion even makes change the vibration character- istics and resistance of the blades, been the cause of the breakage and low performance of the stages. It has often been argued that from the thermodynamic point of view, a cluster of drops behaves, in fact, as one large drop of the same dimension as the cluster. Classical nucleation theory is built on the thermodynamics treatment of drop- lets by the capillarity approximation, where the small droplets have the same properties as bulk condensed phases, with bulk surface properties [5] and considered as a drop. There also would be occasional clusters con- taining a larger number of molecules; however, a motion picture of these larger clusters would show that most are very short lived; they grow rapidly and then shrink rap- idly. Nucleation occurs when a cluster of two, three, four, grows (fluctuates in size) to a size large enough that it then continues to grow rather than shrink [6]. Eventually, agglomeration by coalescence of large clusters enters until thermodynamic equilibrium [7] colliding with each other, forming larger clusters [8], and these drops with several sizes always have a spherical shape, which are forced by the surface tension and keeping constant into the turbine, impacting on the blades and causing dam- ages. 2. Droplets Formation in Steam Turbines Erosion is of significance when drops impact on a hard surface. The continuous impact of drops forms a liquid film on the surface, which would attenuate the forces during the impact at subsequent times and, hence, the long-term wear on the surface [9]. In the last stages of the turbines, very high expansion rates are achieved, leading to supercooled flow condi- tions and nonequilibrium droplet formation by several mechanisms that mean an impact on turbine efficiency. The two-phase flow behavior in a low pressure section of a conventional steam turbine beginning with the first transition, localized in the stator in the third stage denot- ing the saturation line, where, under equilibrium, as- sumptions phase transition would appear, as is seen in Figure 1. Generally, in the third rotor stage is found heteroge- neous nucleation transition. In the fourth stator stage can creates the primary nucleation toward the shroud and occurs in the following stage component (the third rotor). As flow expansion continues into the final stage, signifi- cant supercooling is again possible, leading to further secondary homogeneous nucleation along the final rotor stage. Finally, smaller droplets generated along the inlet third rotor stage and output third rotor stage can collect on blades and be re-entrained, as secondary droplets, into the flow at the trailing edges of rotating components, in particular. Importantly, the droplets generated along the inlet of third rotor blades through fifth rotor stage remain quite small, can be adequately approximated with a no-slip assumption relative to the continuous vapor phase. In the last stage of the low pressure steam turbine the droplets localized have sizes that are generally greater than 100 µm [10] and have a considerable slip relative to the vapor. These droplets have a significant influence on blade erosion, and the fact that the small nucleated drop- lets provide the source for entrainment of large droplets into last stage, describe a highly coupled two-phase flow system. The process of steam expansion on the rows is very complicated. The drop velocities are different of the steam velocity as much by their magnitude as by their direction; in fact, it can’t give a general scheme of the movement of wet steam. The path of the droplets in the channel of the blade rows can be different, as is shown in Figure 2. In this case, the drops in the steam flow can lose their stability and be divided [11]. When the wet steam expands in the row stator blades, the additional condensation of the steam takes place, which it depends of the dimensions that have the drops of the liquid phase. The drops accelerate by the steam Figure 1. Phase transition in a low pressure section of a steam turbine. Stator and rotor components labeled with S and R, respectively. Copyright © 2011 SciRes. EPE  F. R. MARTÍNEZ ET AL.229 Figure 2. Path of droplets in the channel of blade rows [12]. flow; in addition, while greater are the size drops, less will be their velocity in comparison with the steam. Part of the humidity is deposited on the blade surface, forming a fine liquid film (of ordinary, no more than 0.1 mm), which, under the action of the friction forces of the steam flow, is slipped slowly towards the trailing edges. The drop that leaves of the blades of the stator rows with smaller velocity has a direction of the relative velocity and impacts against the suction side of the rotor blade. w By consequence, on the performance of the stage the losses due to steam (where = TS – T) differ- ence between the local saturation temperature TS and measurement temperature T) and the mechanical interac- tion of phases not only exert influence, but also the ac- tion of the wet steam, the energy consumption to trans- port the liquid films by the blade surface, under the ac- tion of centrifugal forces and other factors, they are characteristic for the stage altogether. With the increment of steam pressure, the influence of the weak moisture in the characteristics of the rows reduces the droplet dimen- sions. The erosion can affect a considerable percent of profile (sometimes to 0.2 - 0.3 of chord) causing the loss of portion of the blade. Insignificant erosion even makes change the vibration characteristics and resistance of the blades, been the cause of the breakage, as well as the performance of the stages diminishes [13]. TT The effect of the interaction of the boundary layer and the condensation is localized in the outer part of the (turbulent) boundary layer where considerably larger droplets appear in the (inviscid) core flow of the same cross section. The reason for this effect is that in the outer part of the boundary layer less droplets are formed (lower nucleation rate) than in the core flow of the same cross section. However, these droplets grow faster and get therefore larger since the reduction of the supersatu- ration, i.e. the driving force of the growth, decreases slower. This is, because the faster growth of the lower number of droplets produces less condensate than the weaker growth of the larger number of droplets in the core flow and thus causes a slower reduction of the su- persaturation. It has been observed that in low pressure section occurs a decrement of the quality, beginning with values without greater risks (x = 98%), till reaching lower qualities (x = 90%) in the last stage [15]. The blades, while working with this wet steam, suffer the constant action of the impact of the liquid microparticles, having as a consequence, the erosion of their surface (see the example in the Figure 3 of a drop impacting on the rigid surface). The considerable quantity of steam humidity added to the blade velocities, especially in the last one, is an im- portant factor that has influence on the appearance of erosion on the geometrical parameters of the turbine, the design of the blades (height, chord, axial distance, stage number, pass, entrance angles and exit profile, angles of the bladeness, etc.) and has a direct incidence on the ve- locity, as is shown in the Figure 4, where is noted in the blades the damage by the erosion phenomenon. Figure 3. Drop impacting on the rigid surface [14]. Figure 4. Coordinates of stator blade. Copyright © 2011 SciRes. EPE  F. R. MARTÍNEZ ET AL. 230 The steam velocity and their influence on the charac- teristics of clusters in condensed water vapor affect the performance of the steam turbine, and the blades are oc- casionally damaged by erosion due to the interaction with this condensed water. However, the accurate me- chanism of the erosion is still unknown [16]. As an analysis is examined a size of droplet, R = 7.52 μm, and a cluster compound of 26 molecules of water [17] calculated for a steam turbine of 300 MW [18]; this average cluster can be dangerous for the blade. It is shown that the value obtained about the critical radius from free energy is 0.0023 μm and is observed the direct condensation from the vapor at a rate βi of 2.22 × 1021 molecules per unit interfacial area per unit time. They can shrink by evaporation of molecules to the vapor and by evaporation of molecules to the adsorbed layer. Also it is observed that the critical radius is identical for the homogeneous and heterogeneous nucleation. Usually, the homogeneous nucleation has more prob- able that appears and is required a less atoms in the het- erogeneous nucleation to achieve a nucleus of a radius that is superior to the critical, although it has the same value that in the homogeneous nucleation. The mean free path of the gas molecules is , aver- age distance covered by a particle between collisions with other moving particles, necessary to follow the growth of the droplets in a condensation environment, applying an energy balance around a spherical droplet model undergoing phase change. 2 ˆ3.06 10μml When droplets reaches considerable collision veloci- ties of drops on the blade, the impact pressure of the drop ΔP can surpass the creep limit of the metal and produces on the surface a residual deformation. Nevertheless, it has been determined experimentally that at smaller colli- sion velocities (300 m/s), it even causes the wearing by erosion, due to the breakage by fatigue of the boundary surfaces by the action of the multiple shocks of the drops, which serve as concentrators of tensions and lead later to the destruction of isolated zones and the deterioration of the metal of the blades. For the case of this steam turbine, the great velocities in the last stages, in the order of 500 m/s, displayed loss mass in approximately 4% of the total mass of blade, appearing cavities of 6 mm and wearing areas by erosion of impact drops of 58 × 190 mm2 to the length of blade. The numerous microscopic surface irregularities in the material that conform the blade, may act as nucleating sites [19]. All this values are considered in the nucleation theory for the calculation of energies and rates for homogeneous and heterogeneous nucleation and can compare them and understand their original causes. For this low pressure steam turbine in the last stage is observed that, when increasing the contact angle between surface cluster and environment increments the critical free energy of the cluster, as in the homogeneous case as in the heteroge- neous case. At the same time, increases the free energy of formation of a cluster on a surface for both cases, while decreases the net number of clusters per unit time which grow larger than the critical size. But, it is impor- tant to remember the differences between the problems conditions and what kind of particles are taking into ac- count or, like in this case, it’s not considered water chemistry issues. In the steam turbines the situation is that, particularly, is not possible to predict the droplet size distribution in a correctly form only with the turbine geometry and the inlet and exhaust steam conditions. As it were observed in the last section I, in the Figure 1, exists different stages where the phases of nucleation take form and ap- pear the homogeneous and heterogeneous cases, indicat- ing clearly the differences between levels of energy for the born of each one. For homogeneous nucleation, the phase occurs of spontaneous way from the vapor phase and usually needs more ΔT than the heterogeneous case. Homogeneous nucleation creates droplets with the criti- cal radius of the germs, while the heterogeneous nuclea- tion creates droplets with similar size of the initial chem- istry contaminant. The understanding of the equations of the nucleation theory, is an essential prerequisite to cal- culate the features of the born of droplets responsible of dangerous wetness, related to the behavior of the steam turbines with erosion problems in their blades. A little knowledge of the physical processes involved is the main problem for better advances. The existence of water droplets formation presents practical difficulty concern- ing to the behavior of steam in turbines. The impact of droplets on the blade surfaces is essentially based in the range of particles with sizes affected by the forces of inertia. These droplets cannot follow the stream of the steam flow in the blade cascade. The water becomes to escape from the stator blades in form of large drops, generally toward the suction side of the following rotor blade, causing there erosion problems. The movement of water on the blade channel is the distribution of velocity and local density of steam. As condition for the calcula- tion of the drop movement, first the velocity field of the steam in the blade cascade with a procedure suitable for transonic condition is needed. The calculation of the ve- locity distribution permits the treatment of generation of a stator blade mesh in a programmable code develop- ment for this work. 3. Calculation of Transonic Velocity Fields For a calculation of the transonic stream, the time step procedure is suitable. In future, the ideal gas with con- Copyright © 2011 SciRes. EPE  F. R. MARTÍNEZ ET AL.231 stant relationship of the specific thermal capacities k is accepted for a medium of flow, and the isentropic state change and the well-known gas dynamics basic relations are described. If this condition prevails in t = 0 and if is kept as con- stant t > 0, then an iterated transition adjusts itself to a stationary condition, which is the flowing state searched. The theory determines this temporal transition, which offers the advantage that the problem receives a para- bolic character everywhere in the field, since the solution in the time t + Δt from t, is sufficiently closed in the final state. However, first the law of change of state is ac- cepted as polytropic, in accordance with 1 1 , n pp (1) the index 1 always refers about flow condition. The polytropic exponent n is given by 1. 11 p n n (2) In each case, the base factors serve to the Mach num- ber and speed sound in the flow, which provide the index 1, and the small quantities with the index R. 1 1 1 , p a (3) 1 1 1 , c Ma (4) 1 2 11 1 1 2 R pp M , (5) 1 1 1 . R R p p (6) A condition for the application of the Equation (6) is that the function of the mesh and the leading edge cross- ing compression shocks are weak. It is accepted that in the flow, the angle 1 takes place. In the zone of flow of the mesh profile the velocities of the compressible stream with the given variables of state become pressure and density of inlet and outlet plane after is calculated 1 221 1 R RR pp cp , (7) In the outline of the profile the condition is fulfilled if the velocity is tangential. Thus is possible if the velocity, pressure and density of the fields regarding the size in the inlet and outlet plane linear can be interpolated. In the closest section lmin the exit angle 2 in the fol- lowing form can be written: 1 11 11 21 21 2 min 222 11 sin1 , 22 isis is lMM t (8) min 2 sinfor 1.0, is is lM t 2 (9) with 1 21. 1 R is p Mp (10) Then, the theoretical exit angle 2is of the mesh turbine results in the case of isentropic expansion on a given pressure side. The velocities in x and y direction toward the trailing edge are calculated 2 2 π cos , 2 π sin. 2 xis yis cc cc (11) The velocity, pressure and density fields are intro- duced as initial values for the iterative methods. The pressure sizes p1 and p2 are well-known from the given state of flow. Also is known c1 and c2 in each case with p1 and p2 from the Equation (7). In Equation (2) the polytropic efficiency p considers the friction in sum- mary way and allows to understand the friction strength constantly distributed in the area. It can suppose the field strength per mass unit, in the direction of the increasing meridian coordinate against the each point n'. Then is d ddd p Fn Tsh , (12) dd p hp, (13) d d1 p p Fn . (14) If these equations are divided by dn', then dp/dn' re- places in such a way the developing Δp/Δn', where Δp and Δn' are the total differences from inlet to outlet; then 1p p Fn (15) where is an average value of the density. Thus, the polytropic exponent n and the friction force F can be determined for a given ηp. For the transition the continu- ity equation applied on the volume element ΔVk reads Copyright © 2011 SciRes. EPE  F. R. MARTÍNEZ ET AL. Copyright © 2011 SciRes. EPE 232 1sincos d xy cc tV bs (16) The circulation is extended thereby over the whole element. Thus the impulse equation () sin cossin d xk xyx c Vccc t bs VF p where ij is the angle of inclination of the side that connects the points designated with i and j. For the rep- resentation of the calculation procedure, the dimen- sionless formulation may be introduced in addition of the following definition: 1 : b Bb Stream width. (17a) : ij ij a s Sl Length of the element. Therefore 1sin cossin d xk xyx ccccp tV bs F 2 1 : a V Klb Volume of the element. (17b) 2 11 1 : p PaM Pressure. In the same way the impulse equation in tangential di- rection is deduced itself. 1sin coscosd xk xy y c t cc cpb V 1 : Density. s (18) 2 1 : a lF c Friction Force. 11 : x c Uc Axial Velocity. The circulations can be represented as sums of the connected distances Δsij, in each case are multiplied by the average value integrating along the distance. The Equation (16) is read 11 : y c Vc Peripheral Velocity. Here, index 1 refers to the inlet level, with dependence of time t = 0. The axial width of the mesh is la. Then the Equations (16), (17), (18) and (1) are represented in next (20), (21), (22) and (23). 1(sin cos) 2 (sin cos) ixiij yiij i j xjij yjijjij cc cc b b s (19) 1sin cossincos 2iijiijijijjijj ij MUVBU VB K S 1 1 1sincossincossin 2 jj ii iijiijjijjiji ijjijij ij UB UB UMUVUVBPBPS M K , 1 1sin cossincoscos 2 jj ii iijiijjijjiji ijjijij ij VB VB V M UVU VBPBP K S 1 n PP and the magnitude of Uk, Vk, k in the time + and the Equation (23) are associated to Pk. On the basis of U, V, P and into all points in the mesh in a stream value the temporal derivatives Equa- tions (20)-(22) can be calculated 4. Particular Data of Stator Blade in the Last Stage of Low Pressure , U UU (24) , V VV The presented equations previously are discretized to reach the development of the programming code of cal- culation procedure when coming out of this set of blades when the flow has certain humidity degree. The main (25) , (26)  F. R. MARTÍNEZ ET AL.233 detail is to know the behavior and the influence in the geometry that can have this type of damages that are had in the blades in normal operation. The set of blades must be analyzed of several forms: one of them is considering the amount of drops by cloudiness that exists in the same steam when it begins to become water and cause dam- ages in the trailing edge of the blades stators as a set, appearing erosion problems, that they essentially cause damages in the edge of entrance of the crown rotor blades. Then is had the analysis of the influence of water in the flow, seeing this like loss of damage of the wet steam. In this part of work the results are presented in ac- cording to droplet contact angle θ and its influence over the characteristics of clusters conformed by certain number of molecules approximately. The mean values obtained from each case in where is taken the contact angle is shown in the Table 1. The condensation on the last stage of this steam tur- bine shows the phase change may be governed by ho- mogeneous nucleation and the nonequilibrium process of condensation. It is known that condensed water vapor affects the performance of the steam turbine, and the blades of the steam turbine are occasionally damaged by erosion due to the interaction with this condensed water. The nuclei are assumed to be spherical, chemically inert, equal in size, with a smooth surface and the interface has zero thickness. The contact angles employment for calculating differ- ent equations presented were selected grated than zero and less or equal to 90˚, due to the content of partially wetting. The nucleation model used for introducing val- ues of calculation of the program shows that the value obtained about the critical radius from free energy is 0.0023 µm and it is observed a condensate cluster with a number of possible orientations of 26 molecules. They Table 1. Resulted according to the contact angle. VARIABLE θ = 30˚ θ = 45˚ θ = 60˚ R (droplet radius) 7.52 μm r * (critical radius) 0.0023 μm J (nucleation rate) 8.95 × 1024 8.15 × 1024 7.58 × 1024 C r (cluster radius) 800 μm G* (critical Gibbs energy) 1.51 × 10–21 6.82 × 10–20 18.37 × 10–20 Ghom (homogeneus, Gibbs energy) 1.338 × 10–3 6.04 × 10–3 16.26 × 10–3 G (Gibbs energy) 1.33 × 10–3 T (TS – T) 13.87 K i (molec/L2*t) 2.22 × 1021 can shrink by evaporation of molecules to the vapor and by evaporation of molecules to the adsorbed layer. Here is presented the particular characteristics data of bidimensional flow in the used stator blade (Figure 4) into the program code. Considerations of bidimensional steam flow: Subsonic-transonic, Inviscid, Compressible, Stationary, Free of friction before and later of the blade channel, Cluster as a drop is spherical, Constant diameter size of drop is 100 μm, Boundary layer in surface of profile. Flow properties of wet steam on stator blade: Inlet temperature = 64.5˚C, Inlet pressure = 0.245 bar, Inlet steam quality = 0.89, Inlet flow angle = −5 degree, Inlet blade angle = −5 degree, Inlet axial velocity = 64.49 m/s, Inlet tangential velocity = −5.63 m/s, Inlet stator Mach number = 0.142, Exit temperature = 55.7˚C, Exit pressure = 0.163 bar, Exit steam quality = 0.892, Exit flow angle = 72.3 degree, Exit blade angle = 73.9 degree, Exit axial velocity = 83.2 m/s, Exit tangential velocity = 278 m/s, Exit Mach number = 0.655. Considerations of code: Number of coordinates of the profile (x, y), Number of nodes x, Number of nodes y , Interval between nodes = 0.00080808, Long of the profile = 0.0495 m, Beta in rad, −0.08726. The approximate results of calculation to the station- ary solution was effectuated several times and examined. For the demonstration of the possibility of the inflow angle changes and the influence of the stagnation point situation, the calculation for the lattice with the poly- tropic efficiency is presented. 5. Results It is observed that the critical radius is identical for the homogeneous and heterogeneous nucleation. It is usually that the homogeneous nucleation will be more probably that creates and it is required a less atoms in the hetero- geneous nucleation for achieving a nucleus of a radius that be superior to the critical, although it has the same Copyright © 2011 SciRes. EPE  F. R. MARTÍNEZ ET AL. 234 value that in the homogeneous nucleation. The size of drop is R = 7.52 µm and the radio of the cluster that cause damages by erosion in the rotor blades is rc = 800 µm with a homogeneous nucleation volume of 1.73 × 10−10 m3 and with a heterogeneous nucleation volume of 2.94 × 10−11 m3. For calculating the equations presented here it was taken a cluster with 26 molecules of water. This is an average cluster that can be dangerous for the blade, due to its size. Optical measurements in turbines show that the mean droplet diameter is considerably lar- ger, typically in the range 0.3 - 0.7 mm, and the distribu- tion is much broader, typically from to 1.0 mm. The droplet temperature TP obtained as a function of droplet radius is TP = 359.12 K considering the temperature at conditions of pressure in the last stage. In Figures 5 to 12 are showed a clear difference be- tween suction and pressure velocity and proves the ef- fects of the rear stagnation point in the flow. In the graphic of total enthalpy (Figure 10) shows that for certain number of time steps, presents convergence in the calculation. The total enthalpy is constant only in a stationary system. The simplification of the equation system was possible introducing the constant specific total enthalpy for the entire computing area. In Figure 11 the border drop course for the blade pres- sure side is showed, i.e. the course of the drop affects directly before the outlet of the stator surface. The dis- tance of the border drop course from the blade increases directly with the drop radius, showing the drops ejected to the pressure side directly. Figure 5. Velocity and pressure pattern. Figure 6. Direction of flow in calculated zone. Figure 7. Velocity and pressure pattern. Copyright © 2011 SciRes. EPE  F. R. MARTÍNEZ ET AL.235 Figure 8. Isobars of flow zone. Figure 9. Velocity and pressure pattern. Figure 10. Total enthalpy. Figure 11. Streamlines in blade cascades. 6. Conclusions In this first part of the work, the erosion phenomenon is seen as a technological problem that is tried to analyze in Copyright © 2011 SciRes. EPE  F. R. MARTÍNEZ ET AL. 236 Figure 12. Mass flow and stream mass density . the greater possible degree. It is only possible to be di- minished, is not possible to be eliminated; therefore, the study of the erosion is necessary from its origin, the analysis of the phenomena that interact in their process of formation, the harmful effect that it causes on the sur- face of the blades, the revision of different recommenda- tions from protection against the erosion and, finally, to give a proposal of its prevention. The analyze carried out in this first part of study can not be used as a base for the calculation of the turbine stages, because the humidity influence over the performance and reaction degree, de- pend also on other geometric and pattern parameters: blades configuration, clearance, relation between surface of the blade crowns, stage to treat, etc. Therefore it is necessary to have efficient technological procedures to avoid the damages not only in the blades but also in the whole turbine, avoiding with this bigger numbers of break downs along the year and increases in cost of maintenance and economical losses caused because of this. For another hand, depending of flow condition and type of design, the shape of the droplets and the sliding coefficient that are going to determine the parameters that have an influence over the mechanical erosion, giv- ing entrance for the investigation of prevention of the blade erosion in the body of low pressure or, at least, to control it, because for the investigation and experimental field it is necessary to have a greater knowledge of the role that the variables have on a micro and macroscopic level, that causes the origin of humidity. In next second part “Theoretical and Numerical Analysis of the Mechanical Erosion in Steam Turbine Blades. Part II”, the problem display the field of veloci- ties with influence of wet in the stator blade mesh in the low pressure section of the turbine. 7. References [1] M. F. Rueda, V. M. Toledo, S. F. Sánchez, H. J. A. Or- tega and M. A. A. Rueda, “Humidity Distribution in a Two Dimensional Stator Blade Cascade of Steam Tur- bine,” 7th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Antalya, 2010. [2] D. Braukmann, Institut für Thermodynamic der Luft und Raumfahrt, uni-sttutgart.de. [3] A. E. Zaryankin, V. A. Zaryankin and B. P. Simonov, “Several Ways of Improving the Efficiency of the Flow Paths of the Steam Turbines,” Thermal Engineering, Vol. 50, No. 6, 2003, pp. 442-448. [4] M. F. Rueda, V. M. Toledo, S. F. Sánchez and M. A. A. Rueda, “Calculation of Drops Distribution in Steam Tur- bine Blades,” 5th European Conference of Economics and Management of Energy in Industry, Algarve, 2009. [5] I. J. Ford, “Thermodynamic Properties of Critical Clus- ters from Measurements of Vapour-Liquid Homogeneous Nucleation Rates,” The Journal of Chemical Physics, Vol. 105, No. 18, 1996, pp. 8324-8332. doi:10.1063/1.472687 [6] J. L. Katz, J. A. Fisk and M. M. Rudek, “Nucleation of Single Component Supersaturated Vapors,” Nucleation and Atmospheric Aerosols 1996: Proceedings of the 14th International Conference on Nucleation and Atmospheric Aerosols, Helsinki, 26-30 August 1996, pp. 1-10. [7] P. P. Wegner and J.-Y. Parlange, “Condensation by Ho- mogeneous Nucleation in the Vapor Phase,” Naturwis- senschaften, Vol. 57, No. 11, 1970, pp. 525-533. doi:10.1007/BF00625319 [8] A. Hanna, “Kinetic Effect of Cluster-Cluster Processes on Homogeneous Nucleation Rates in One- and Two-Com- ponent Systems,” The Journal of Chemical Physics, Vol. 107, No. 8, 1997, pp. 3196-3203. doi:10.1063/1.474669 [9] E. E. Michaelides, “Particles, Bubbles and Drops, Their Motion, Heat and Mass Transfer,” World Scientific Pub- lishing, Singapore, 2006. [10] J. W. P. Schmelzer, “Nucleation Theory and Applica- tion,” Wiley, Hoboken, 2005, pp. 40. doi:10.1002/3527604790 [11] D. W. Oxtoby, “Nucleation of First-Order Phase Transi- tions,” Accounts of Chemical Research, Vol. 31, No. 2, 1998, pp. 91-97. doi:10.1021/ar9702278 [12] V. M. Toledo and W. Riess, “Vorlessung Dampf-turbi- nen,” Institut fuer Stroemungsmaschinen, Universitaet Hannover, Germany, 2008. Copyright © 2011 SciRes. EPE  F. R. MARTÍNEZ ET AL. Copyright © 2011 SciRes. EPE 237 [13] J. L. Katz, “Homogeneous Nucleation Theory and Ex- periment: A Survey,” Pure and Applied Chemistry, Vol. 64, No. 11, 1992, pp. 1661-1666. doi:10.1351/pac199264111661 [14] K. K. Haller, “High-Velocity Impact of a Liquid Droplet on a Rigid Surface: The Effect of Liquid Compressibil- ity,” Thesis, Swiss Federal Institute of Technology Zurich, Zurich, 2002. [15] P. B. Heinz, “Guía Práctica para la Tecnología de las Turbinas de Vapor,” McGraw Hill, New York, 1996. [16] S. Yamamoto, “Computation of Practical Flow Problems with Release of Latent Heat,” Elsevier, Amsterdam, 2004. [17] M. F. Rueda, V. M. Toledo, L. G. Jarquín, S. F. Sánchez and G. Polupan, “Erosion Study of a Rotor Blade from a Steam Turbine,” 6th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Pretoria, 2008. [18] M. F. Rueda, V. M. Toledo, M. I. Carvajal, F. J. Abugaber and E. G. Tolentino, “Estudio Teórico de la Erosión Mecánica en un Álabe Rotor del Último Paso de la Sección de Baja Presión de una Turbina de Vapor de 300 MW,” Científica Journal, Vol. 11, No. 3, 2007. [19] J. C. Bellows, “Chemistry in the Moisture Transition Region of the Steam Turbine,” Journal of Solution Chemistry, Vol. 32, No. 10, 2003. |

