Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63510,4 pages
10.4236/jamp.2016.42027
Quest for Potentials in the Quintessence Scenario
Tetsuya Hara
Department of Physics, Kyoto Sangyo University, Kyoto 603-8555, Japan



Received 3 January 2016; accepted 13 February 2016; published 17 February 2016
ABSTRACT
The time evolution of the equation of state w for quintessence scenario with a scalar field as dark energy is studied up to the third derivative (d3w/da3) with respect to the scale factor a, in order to predict the future observations and specify the scalar potential parameters with the observables. The third derivative of w for general potential V is derived and applied to several types of potentials. They are the inverse power-law (V = M4 + α/Qα), the exponential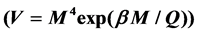 , the mixed
, the mixed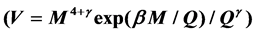 , the cosine
, the cosine 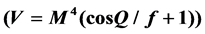 and the Gaussian types
and the Gaussian types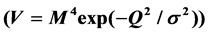 , which are prototypical potentials for the freezing and thawing models. If the parameter number for a potential form is n, it is necessary to find at least for n + 2 independent observations to identify the potential for0m and the evolution of the scalar field (Q and
, which are prototypical potentials for the freezing and thawing models. If the parameter number for a potential form is n, it is necessary to find at least for n + 2 independent observations to identify the potential for0m and the evolution of the scalar field (Q and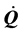 ). Such observations would be the values of ΩQ, w, dw/da, ∙∙∙, and dwn/dan. From these specific potentials, we can predict the n + 1 and higher derivative of w; dwn + 1/dan + 1, ∙∙∙. Since four of the above mentioned potentials have two parameters, it is necessary to calculate the third derivative of w for them to estimate the predict values. If they are tested observationally, it will be under- stood whether the dark energy could be described by the scalar field with this potential. At least it will satisfy the necessary conditions. Numerical analysis for d3w/da3 is made under some specified parameters in the investigated potentials, except the mixed one. It becomes possible to distinguish the potentials by the accurate observing dw/da and d2w/da2 in some parameters.
). Such observations would be the values of ΩQ, w, dw/da, ∙∙∙, and dwn/dan. From these specific potentials, we can predict the n + 1 and higher derivative of w; dwn + 1/dan + 1, ∙∙∙. Since four of the above mentioned potentials have two parameters, it is necessary to calculate the third derivative of w for them to estimate the predict values. If they are tested observationally, it will be under- stood whether the dark energy could be described by the scalar field with this potential. At least it will satisfy the necessary conditions. Numerical analysis for d3w/da3 is made under some specified parameters in the investigated potentials, except the mixed one. It becomes possible to distinguish the potentials by the accurate observing dw/da and d2w/da2 in some parameters.
Keywords:
Dark Energy, Quintessence, Thawing Model, Freezing Model

1. Introduction
There are mainly two theoretical viewpoints to explain the accelerated universe. One is related to modification of gravity and the other is associated with vacuum energy and/or matter field theories. Taking the latter viewpoint, we investigate the scalar fields in quintessence scenario how relevant it to the dark energy.
In this scenario, the potential of the scalar field has n independent parameters, so we recognize that in principle n time derivatives of the equation of state with observable ΩQ and w are enough to specify the scalar potentials and to predict the higher derivatives. In the paper [1], we have calculated the third derivative of the equation of state for five scalar potentials to identify the models and to predict the future observations. The first and second derivatives have been investigated in the paper [2].
Usually, the variation of the equation of state w for the dark energy is described by [4]
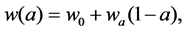 (1)
(1)
where a, w0, and wa are the scale factor (a = 1 at current), the current value of w(a) and the first derivative of w(a) by wa = −dw/da, respectively.
We have extended the parameters pace, in the paper [1],
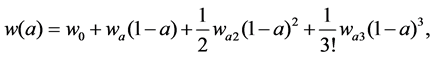 (2)
(2)
where 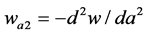 and
and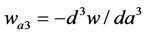 .
.
Recent Planck and other observations for w(z) are shown in Figure 1 [3]. The typical values for each z are adopted and the derived values of dw/da and d2w/da2 are estimated in Table 1.
We follow the single scalar field formalism of Steinhardt et al. (1999) [5] [6] and investigate three potentials for so-called freezing model [7], in which the field is rolling towards down its potential minimum, as V = M4+α/Qα (inverse power law) [8], 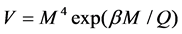 (exponential), and
(exponential), and 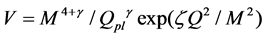 (mixed) [9]. In this freezing model, w(z) approaches to −1.
(mixed) [9]. In this freezing model, w(z) approaches to −1.
We study other two potentials for so-called thawing model, in which the field is nearly constant at first and then starts to evolve slowly down the potential; 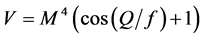 (cosine) and
(cosine) and 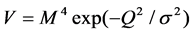 (Gaussian). In this thawing model, w(z) starts from −1 and increases later.
(Gaussian). In this thawing model, w(z) starts from −1 and increases later.
Because four of the above mentioned potentials have two parameters, it is necessary to calculate the third derivative of w for them to estimate the predict values. If they are the predicted one, it will be understood that the dark energy could be described by the scalar field with this potential. At least it will satisfy the necessary
Figure 1. From the observations, the reconstructed equation of state w(z) as a function of red shift z where 1 + z = 1/a [3]. The simulated curves in Table 1 are designated by signs.
Table 1. The values of w(z) for each z are adopted and the values dw/da and dw2/da2 are estimated. The typical values are designated by signs, which are shown in Figure 1 and plotted in Figure 2.
conditions. Numerical analysis are made for d3w/da3 under some specified parameters in the investigated potentials except mixed one which has three parameters [1].
2. Equation of state wQ by a Scalar Field
For the dark energy, we consider a scalar field Q(x,t), where the action for this field in the gravitational field is described in [2].
Neglecting the coordinate dependence, the equations for Q(t) becomes
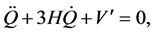 (3)
(3)
where H is the Hubble parameter, over-dot is the derivative with time, and V' is the derivative with Q. The equation of state wQ due to the scalar field is described by
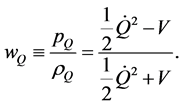 (4)
(4)
We put wQ = −1 + ∆ for the later convenience (0 < ∆ < 0.2).
3. Second, and Third Derivative of wQ
The detailed calculations of the second, and third derivatives of wQ for potentials are displayed in the paper [1]. The numerical calculations for the freezing and thawing models under limited parameters are analyzed there.
In Figure 2, the curve for α = 0 is presented for the case of V = M4+α/Qα with ∆ = 0.1 by the red solid curve in the dwQ/da and d2wQ/da2 coordinates. The signature of α will change beyond the parabolic curve. We assume α > 0, so that the upper part of the red curve is forbidden for this potential and the freezing type potentials as well. The green (inner) dotted curve is the case of 
The interesting point is that the forbidden regions for the freezing type potentials are allowed region for the thawing type potentials and the reverse is also true. It is possible to distinguish the potentials among each type due to the different predicted values of d3wQ/da3 [1], however it is necessary to make accurate observations for the values of dwQ/da, d2wQ/da2, d3wQ/da3 and other parameters such as ∆.
Figure 2. The curve for α = 0 is presented for the case of V =M4+α/Qα with ∆ = 0.1 by the red solid curve in the dwQ/da and d2wQ/da2 coordinates. The signature of α will change beyond the parabolic curve and the upper part is forbidden for the freezing model. The lower part of this curve is forbidden for the thawing model (Gausssian type). The upper part of the green (inner) dotted curve is allowed region for thawing model of 
4. Conclusions
At present, backward observations, such as Planck, baryon acoustic oscillation, Supernova Ia, Hubble constant, weak lensing, and red shift distortion, have been undertaken to estimate wQ at the age (1 + z) as in Figure 1 [3]. From Figure 1, the rough values of w(a = a0), dw/da and d2w/da2 have been estimated which are presented in Table 1. They are pointed in the dwQ/da and d2wQ/da2 plane in Figure 2.
The adopted values from observation show −0.5 < d2wQ/da2< 6 within the region 0.1 < dwQ/da < 0.5. Although there is a lot of uncertainty, at the moment, it seems to be preferable for the thawing model against the freezing model under the comparison with the numerical results and the observations [3].
About observations in Figure 1, it seems to be difficult to accept that the equation of state w = p/ρ is almost smaller than −1 in the region z −1 ~ 2.
Usually matter density increases as



If w < −1 which means ∆ < 0 is correct in Figure 1, we must consider fully different models such as phantom, k-essence, chameleon, tachyon, dilaton, quintom, modified gravity, and so on [10].
Cite this paper
Tetsuya Hara, (2016) Quest for Potentials in the Quintessence Scenario. Journal of Applied Mathematics and Physics,04,211-214. doi: 10.4236/jamp.2016.42027
References
- 1. Muromachi, Y., Okabayashi, A., Okada, D., Hara, T. and Itoh, Y. (2015) Search for Dark Energy Potentials in Quintessence. Progress of Theoretical & Experimental Physics, 2015, 093E01. [arXiv:1503.03678 [astro-ph]]
- 2. Hara, T., Sakata, R., Muromachi, Y. and Itoh, Y. (2014) Time Variation of Equation of State for Dark Energy. Progress of Theoretical & Experimental Physics, 2014, 113E01. [arXiv:1409.2726[astro-ph]]
- 3. Planck Collaborations: Ade, P.A.R., et al. (2015) Planck 2015 Results. XIV. Dark energy and Modified Gravity. [ar-Xiv:1502.01590[astro-ph]]
- 4. Linder, E.V. (2003) Exploring the Expansion History of the Universe. Physical Review Letters, 90, 091301. [arXiv:0208512v1[astro-ph]]
- 5. Steinhardt, P.J., Wang, L. and Zlatev, I. (1999) Cosmological Tracking Solutions. Physical Review D, 59, 123504. http://dx.doi.org/10.1103/PhysRevD.59.123504
- 6. Zlatev, I., Wang, L. and Steinhardt, P.J. (1999) Quintessence, Cosmic Coincidence, and the Cosmological Constant. Physical Review Letters, 82, 896. http://dx.doi.org/10.1103/PhysRevLett.82.896
- 7. Caldwell, R.R. and Linder, E.V. (2005) Limits of Quintessence. Physical Review Letters, 95, 141301. http://dx.doi.org/10.1103/PhysRevLett.95.141301
- 8. Peebles, P.J.E. and Ratra, B. (1988) The Cosmology with a Time-Variable Cosmological “Constant”. Astrophysical Journal, 325, L17-L20. http://dx.doi.org/10.1086/185100
- 9. Brax, Ph. and Martin, J. (1999) Quintessence and Supergravity. Physics Letters B, 468, 40-45. http://dx.doi.org/10.1016/S0370-2693(99)01209-5
- 10. Amendola, L. and Tsujikawa, S. (2010) Dark Energy. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511750823




