Paper Menu >>
Journal Menu >>
 Energy and Power En gi neering, 2011, 3, 246-252 doi:10.4236/epe.2011.33031 Published Online July 2011 (http://www.SciRP.org/journal/epe) Copyright © 2011 SciRes. EPE CFD Simulation of Dilute Gas-Solid Flow in 90˚ Square Bend Tarek A. Mekhail, Walid A. Aissa, Soubhi A. Hassanein, Osama Hamdy Department of Mechanical Power, Faculty of Energy Engineering (Aswan), South Valley University, Qena, Egypt E-mail: walidaniss@gmail.com Received May 11, 2011; revised June 2, 2011; accepted June 10, 2011 Abstract Gas-solid two-phase flow in a 90˚ bend has been studied numerically. The bend geometry is squared cross section of (0.15 m × 0.15 m) and has a turning radius of 1.5 times the duct’s hydraulic diameter. The solid phase consists of glass spheres having mean diameter of 77 µm and the spheres are simulated with an air flowing at bulk velocity of 10 m/s. A computational fluid dynamic code (CFX-TASCflow) has been adopted for the simulation of the flow field inside the piping and for the simulation of the particle trajectories. Simu- lation was performed using Lagrangian particle-tracking model, taking into account one-way coupling, com- bined with a particle-wall collision model. Turbulence was predicted using k-ε model, wherein additional transport equations are solved to account for the combined gas-particle interactions and turbulence kinetic energy of the particle phase turbulence. The computational results are compared with the experimental data present in the literature and they were found to yield good agreement with the measured values. Keywords: Gas-Solid Two-Phase Flow, Dilute, 90˚ Bend, CFX 1. Introduction Bends are a common element in any piping system of gas-solid flow applications such as pneumatic conveyers, pneumatic dryers, chemical industries and food process- ing. The gas-solid flow in bends is affected by complex parameters, such as centrifugal forces, formation and dispersion of ropes, secondary flows and erosion of bend outer walls. The gas-solid flow in 90˚ bend has been studied by many researchers. Yang and Kuan [1] and Kuan [2] performed a CFD predictions of dilute gas- solid flow through a curved 90˚ duct bend based on a Differential Reynolds Stress Model (DRSM) for calcu- lating turbulent flow quantities and a Lagrangian particle tracking model for predicting solid velocities. They found that the more complex DRSM failed to predict the pressure gradient effects that prevail within the bend; the predicted turbulence intensity only bears qualitative re- semblance to the measured distribution. Further, they stated that the mean streamwise velocities based on DRSM display good qualitative representation of the measured profiles while the standard k-ε is able to achieve better quantitative agreement. Levy and Mason [3] studied the effect of the bend on the cross-sectional particle concentration and segregation of solid particles from the carrier gas. They found that the rope region increased as the curvature ratio decreased. Mohanaran- gam et al. [4] and [5] reported a numerical investigation into the physical characteristics of dilute gas-solid flows over a square sectioned 90˚ bend. They employed the modified Eulerian-Eulerian two fluid model to predict the gas-particle flows and studied a dilute gas-particle flows over a square sectioned 90˚ bend employing two approaches to predict the gas-particle flows, namely the Lagrangian particle tracking model and Eulerian two fluid model. The computational results are compared with the LDV results of Kliafas and Holt [6] and were found to yield good agreement with the measured values and the Eulerian model provided useful insights into the particle concentration and turbulence behavior, they found that both Eularian-Eularian and Eularian-Lagran- gian approaches provided reasonably good comparison for gas and particle velocities together with the fluctua- tion for the gas phase. Further, they stated that despite the fact that the particle fluctuation using the Eularian model showed good comparison with the experimental data. They found that the more computational mesh and time is required for Lagrangian particle tracking model in comparison to Eularian model. Ibrahim et al. [7] stud- ied numerically the behavior of gas-solid flow in 90˚  T. A. MEKHAIL ET AL.247 bend using two different turbulence models and they found that the total pressure loss for gas-solid flow in 90˚ bend is greater than the corresponding value obtained for gas only and its value is greatly affected by the fluid and solid parameters. Bradley [8] gives a review of the causes of attrition and wear in pneumatic conveying, the consequences, and the techniques which may be applied to overcome them in a practical context. Tian et al. [9] investigated the performance of both the Eulerian La- grangian model and the Eulerian-Eulerian model to simulate the turbulent gas-particle flow. The validation against the measurement for two-phase flow over back- ward facing step and in a 90˚ bend revealed that both CFD approaches provide reasonably good prediction for both the gas and particle phases. Chu and Yu [10] simu- lated numerically gas solid flow in complex three-di- mensional (3D) systems by means of Combined Contin- uum and Discrete Method (CCDM). They compared the results, quantitatively and qualitatively, with experiment- tal data and good agreement was noticed. Chen et al. [11] investigated the relative erosion severity between plug- ged tees and elbows for dilute gas-solid flow applying a CFD based erosion prediction model. They conducted experimental tests to verify the simulation results. The ratio of erosion at the end of the plugged section to that in an elbow was found to approach a constant value for a range of conditions. A correlation was presented that provides the ratio of erosion of the outer downstream corner of the plugged tee to that in an elbow. Deng et al. [12] studied experimentally the effect of particle concen- tration on the erosion rate of pipe bends in pneumatic conveyors using different bend radii. Results show that there was a significant reduction of the specific erosion rate for high particle concentration. This reduction was considered to be as a result of the shielding effect during the particle impacts. 2. Present Study 2.1. Mathematical Model The purpose of this paper is to provide deeper under- standing of the parameters which may have an effect on the erosion and pipeline wear especially at bends. A CFD simulation of the dilute gas-solid flow in a square-sec- tioned 90˚ bend (0.15 m × 0.15 m) using a Lagrangian particle tracking model is presented, considering that all the particles have been introduced in the flow with ap- proximately the same bulk velocity of the fluid. The par- ticulate phase consists of glass particles that assumed to be spherical with diameter of 77 μm. The Finnie’s ero- sion prediction model [13] and the standard k-ε were applied to numerically predict erosion and turbulence in elbow respectively. The mixture composition and phase velocities were defined at the inlet boundary. The system pressure was fixed at the outlet boundary. The aforemen- tioned models were implemented into the CFX-TASC flow V 2.9.0 via user-defined subroutines. Using user- defined subroutines allows the flexibility in extending the collision model to handle complex engineering flows. To gain confidence in this numerical study, the predicted mean velocities for both gas phase and solid phase were validated against experimental data of Yang and Kuan [1]. 2.2. Assumptions Assumptions made in formulating the tracking model have introduced some limitations on the model. These are: Particle/particle interactions are not included in the model. Particle interactions may be important in flows where the discrete phase volumetric concentra- tion is greater than 1% [14]. This assumption implies that the model is designed for dilute systems. There are no particle source terms to the turbulence equations, and therefore, turbulence is not modulated by the discrete phase. The viscous stress and the pressure of the particulate phase are negligible. Only inert, spherical particles are considered. There is no mass transfer over the surface of the par- ticles due to particle-wall collision. The flow field is isothermal. 2.3. Gas Phase The first step is to solve the continuous carrier fluid flow equations. The continuity and momentum equations em- ployed by the CFX-2.9.0 [15] are given in Equations (1) and (2), respectively: 0 gj gg j u tx (1) 2 3 iji gg ggg j ij ggg l uieffeff ij ijji l uuu tx Puu u S xxxx x (2) where, i g u represents the gas mass-averaged velocities in the xi coordinate directions, P*g is a time-average pressure, ρ is a time-average density, μeff is the effective viscosity, and the S term is an additional time-average source term. Copyright © 2011 SciRes. EPE  T. A. MEKHAIL ET AL. 248 2.4. Solid Phase After obtaining the flow field, the particle trajectories are simulated. In the current model, the particles are as- sumed not to affect the flow field, one-way coupling between the sand particles and the carrier fluid, the fluid is allowed to influence the trajectories but the particles do not affect the fluid. It is noted that the one-way cou- pling method is suitable only for low solid loading. The particles are introduced at a finite number of starting locations. In every given time step, their positions and velocities are calculated according to the forces acting on the particle and using Newton’s second law. The equa- tion of motion for a par- ticle [15] can be written as: 0 0 3 3 2 dπd 3π d πdd 12 dd dd 3dd πd 2 6d p gg pcorgp tgg p e t gp t g t u mdCuu t duu F tt uu tt dt tt du t p (3) where, mp is particle mass, d is particle diameter, u is velocity, ρ is density, μ is fluid dynamic viscosity, Ccor is drag coefficient and t0 is the starting time. The subscript g and p refers to the fluid gas and the particle respec- tively. The term on the left-hand side is a summation of all of the forces acting on the particle expressed in terms of the particle acceleration. The first term on the right hand side is the viscous drag of fluid over the particle surface according to Stokes law. The second term is the force applied on the particle due to the pressure gradient in the fluid surrounding the particle caused by fluid accelera- tion. The third term is the force to accelerate the virtual mass of the fluid in the volume occupied by the particle. The fourth term is an external force which may directly affect the particle such as gravity or an electric field. The fifth term is the Basset force or history term which accounts for the deviation in flow pattern from steady state. A drag coefficient, Ccor, is introduced to account for experimental results on the viscous drag of a solid sphere. For a moderate particle Reynolds number 0.01 < Rep < 260, the drag correction in Equation (8) [15] is: 0.6305 0.82 0.05 10.1935(Re)Re 20 10.1315ReRe 20 p cor pp C (4) where, log Re p (5) where, the particle Reynolds number, Rep, is calculated from: Repggp d (6) In turbulent tracking, the instantaneous fluid velocity is decomposed into mean, g , and fluctuating, g , components. 2.5. The Particle-Wall Collision When a particle impacts on the pipe wall, it reflects at an angle related to the coefficient of restitution, er. The value of er determines the component of velocity normal to the surface after impact, , given the incident nor- mal component, r u i u : rr ueu i (7) The coefficient of restitution is taken to equal unity. Figure 1 shows the elastic collision for er equals to unity, where, 12 (8) 2.6. Particle Erosion Model Before conducting the flow calculations, it is necessary to modify source code to calculate particle erosion on the duct and pipe walls. To calculate the erosion a simplified Finnie's erosion model [13] is applied. Finnie proposed that erosive wear is a direct consequence of the cutting of surfaces by impacting particles. This model assumes that the erosion rate on a surface; ER may be described by: n ERKV f (9) where, V is the impact velocity of the particle on the sur- face, K and n are erosion parameters, and f(θ) is a func- tion relating wear to the impact angle (angle relative to the surface normal), θ: 2 2 1sin0 0.4π 3 sin 23cos0.4π f (10) Figure 1. Elastic collision (coefficient of restitution = 1). Copyright © 2011 SciRes. EPE 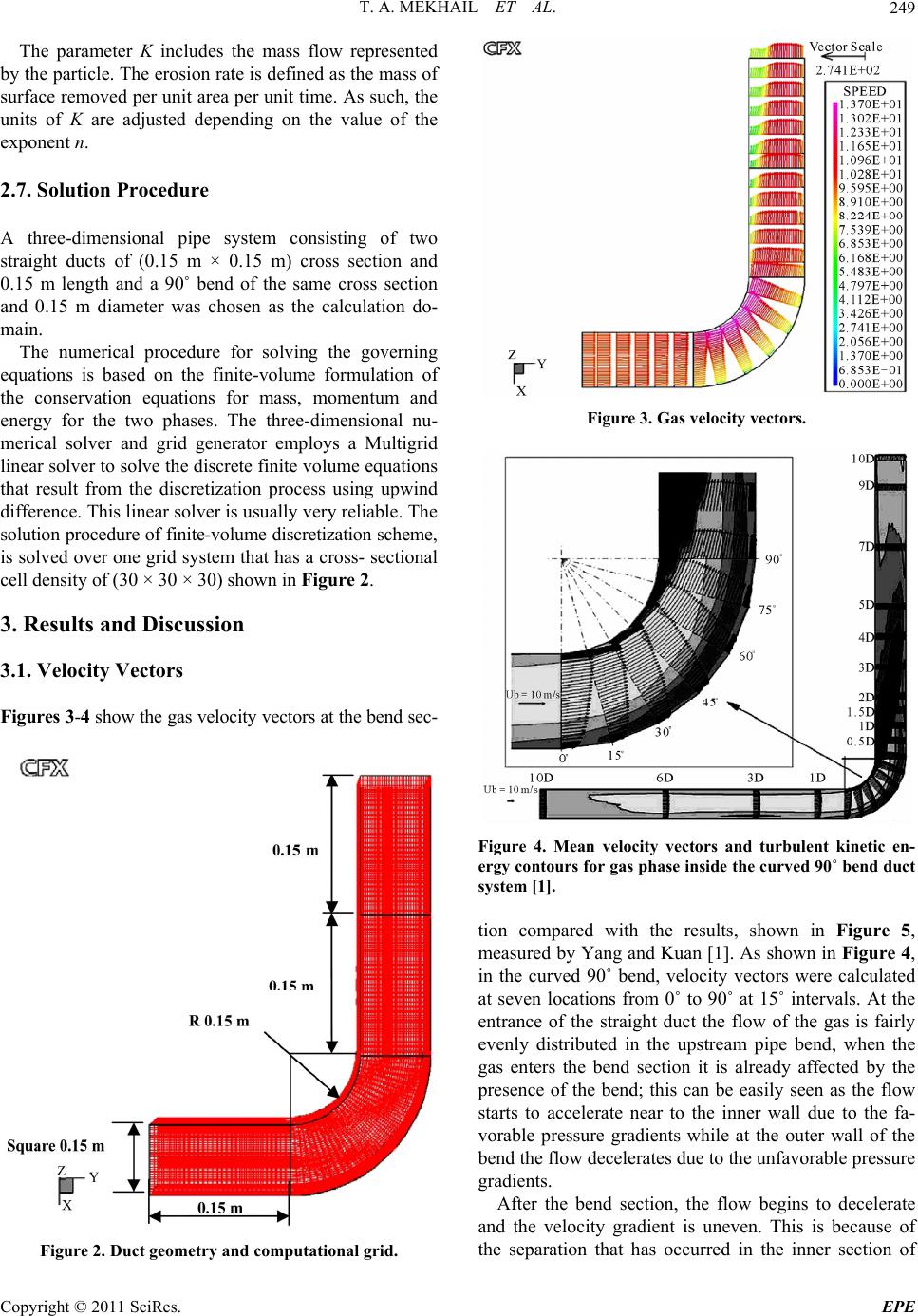 T. A. MEKHAIL ET AL.249 The parameter K includes the mass flow represented by the particle. The erosion rate is defined as the mass of surface removed per unit area per unit time. As such, the units of K are adjusted depending on the value of the exponent n. 2.7. Solution Procedure A three-dimensional pipe system consisting of two straight ducts of (0.15 m × 0.15 m) cross section and 0.15 m length and a 90˚ bend of the same cross section and 0.15 m diameter was chosen as the calculation do- main. The numerical procedure for solving the governing equations is based on the finite-volume formulation of the conservation equations for mass, momentum and energy for the two phases. The three-dimensional nu- merical solver and grid generator employs a Multigrid linear solver to solve the discrete finite volume equations that result from the discretization process using upwind difference. This linear solver is usually very reliable. The solution procedure of finite-volume discretization scheme, is solved over one grid system that has a cross- sectional cell density of (30 × 30 × 30) shown in Figure 2. 3. Results and Discussion 3.1. Velocity Vectors Figures 3-4 show the gas velocity vectors at the bend sec- Figure 2. Duct geometry and computational grid. Figure 3. Gas velocity vectors. Figure 4. Mean velocity vectors and turbulent kinetic en- ergy contours for gas phase inside the curved 90˚ bend duct system [1]. tion compared with the results, shown in Figure 5, measured by Yang and Kuan [1]. As shown in Figure 4, in the curved 90˚ bend, velocity vectors were calculated at seven locations from 0˚ to 90˚ at 15˚ intervals. At the entrance of the straight duct the flow of the gas is fairly evenly distributed in the upstream pipe bend, when the gas enters the bend section it is already affected by the presence of the bend; this can be easily seen as the flow starts to accelerate near to the inner wall due to the fa- vorable pressure gradients while at the outer wall of the bend the flow decelerates due to the unfavorable pressure gradients. After the bend section, the flow begins to decelerate and the velocity gradient is uneven. This is because of the separation that has occurred in the inner section of Copyright © 2011 SciRes. EPE  T. A. MEKHAIL ET AL. 250 (a) (b) (c) (d) Figure 5. Particle trajectories of different particle diame- ters. (a) Dp = 10 µm; (b) Dp = 40 µm; (c) Dp = 77 µm; (d) Dp = 120 µm. the bend due to the adverse pressure gradient. 3.2. Effect of Particle Diameter on the Particle Trajectories Figure 5 shows the trajectories of particles tracked in a wide range of particle diameters. It can be seen that the particles with small diameters (case (a) Dp = 10 µm) tend to follow the flow and turning before reaching the outer wall while the particles with large diameters (cases (b,c and d) Dp = 40, 77 and 120 µm respectively) don't follow the flow and hit the outer wall of the bend. With the in- crease of Dp the concentration of particles is further in- creased near the outer wall and further decreased near the inner wall. Further progresses of the flow into the bend, a particle free region starts to be identified close to the inner wall, the thickness of this particle free region gradually increases until the bend exit with the increase of the particle diameter. 3.3. Effect of Particles on Gas Speed The velocity field with and without particles injected is compared to determine the relative influence of the glass particles on the fluid flow. Two separate calculations were made: with and without particles. The speed in the duct is compared through the relation: dif_speed = speed – speed_wop (11) where, dif_speed is the difference in velocity, speed is the gas velocity with particles and speed_wop is the gas velocity without particles. Figure 6 shows the velocity vectors for the gas phase with and without particles. The difference in velocity for the flow with and without particles is shown in Figure 7. The velocity field has been substantially changed by the particles. As shown in Figure 7 there is no observed speed difference in the entrance of the duct, as the parti- cles supposed to be entered with the same gas velocity (10 m/s). The speed starts to decrease slightly at the be- ginning of the bend section near to the outer wall, this may be due to the increasing in particle concentration at this region. The difference in speed downstream of the bend is negative, speed is further decreasing especially at the inner wall of the duct, where particles coming from the first impact at the bend hit again the inner wall of the downstream duct. Particles may move faster than the gas phase or may lag behind the gas phase. Depending on the movement of the particles they setup slip velocities. These slip velocities in turn give rise to particle drag. The gas phase which is embodied with these particles, lose some of its velocity trying to overcome this drag. This helps to explain why the gas flows with particles lag behind the clean gas which has no particles. 3.4. Erosion The erosion information was generated based on Finnie’s model which described earlier. Erosion was calculated on all duct surfaces and plotted as shown in Figure 8. The current model shows that, any part of the pipe sys- tem that experiences high flow velocities or sudden changes in flow direction is subjected to erosion. The rate of particle erosion is highly dependent on the flow velocity. As stated in Equation (9). the erosion rate is a function of (Vn), then any small increases in velocity can therefore cause substantial increases in erosion. The peak erosion rate occurs at the outer wall of the bend section; where the particle impacts, are concen- trated. Particle size mostly influences erosion by deter- mining how many particles impact on a surface. Very small particles (~10 microns) are carried with the fluid and rarely hit walls, see Figure 5(a). As they are lighter, small particles more readily follow the flow of the car- Copyright © 2011 SciRes. EPE  T. A. MEKHAIL ET AL. Copyright © 2011 SciRes. EPE 251 (a) (b) Figure 6. Velocity vectors of gas phase with and without particles. (a) Velocity vectors of gas phase only; (b) Velocity vectors of gas phase with particles. Figure 7. Change in velocity field due to particle flow. Figure 8. Erosion pattern on the duct wall. rying fluid rather than impacting on the walls. Also, when they impact they tend to do so at low angles and they cause less damage. Larger particles tend to travel in straight lines and bounce off surfaces. So, the higher the free stream velocity and the larger the particle size, the more the erosion will be. ent diameters, also the erosion pattern is predicted. The mean velocity vectors of the predicted model shows good agreement with the experimental data obtained by Yang and Kuan [1]. The current numerical data can be used to further enhance CFD models, to aid better pre- diction near the inner wall of the bend by establishing an effective two-way coupling between the gas and the par- ticulate phases. 4. Conclusions The current study simulates gas and solid phases in a dilute two-phase flow system inside a square sectioned 90˚ bend using CFD. The computational results obtained by Lagrangian tracking model explain how the flow in- side the duct would be and show the shape of the gas velocity vectors and the particle trajectories with differ- 5. References [1] W. Yang and B. T. Kuan, “Experimental Investigation of Dilute Turbulent Particulate Flow inside a Curved 90˚ Bend,” Chemical Engineering Science, Vol. 61, No. 11, 2006, pp. 3593-3601. doi:10.1016/j.ces.2006.01.013  T. A. MEKHAIL ET AL. 252 [2] B. T. Kuan, “CFD Simulation of Dilute Gas-Solid Two-Phase Flows with Different Solid Size Distributions in a Curved 90˚ Duct Bend,” The Australian and New Zealand Industrial and Applied Mathematics, Vol. 46, 2005, pp. C744-C763. [3] A. Levy and D. J. Mason, “The Effect of a Bend on the Particle Cross-Section Concentration and Segregation in Pneumatic Conveying Systems,” Powder Technology, Vol. 98, No. 2, 1998, pp. 95-103. doi:10.1016/S0032-5910(97)03385-8 [4] K. Mohanarangam, Z. F. Tian and J. Y. Tu, “Numerical Simulation of Turbulent Gas—Particle Flow in a 90˚ Bend: Eulerian—Eulerian Approach,” Computers and Chemical Engineering, Vol. 32, No. 3, 2008, pp. 561-571. doi:10.1016/j.compchemeng.2007.04.001 [5] K. Mohanarangam, Z. F. Tian and J. Y. Tu, “Numerical Computation of Turbulent Gas-Particle Flow in a 90 De- gree Bend: Comparison of Two Particle Modeling Ap- proaches,” The Australian and New Zealand Industrial and Applied Mathematics, Vol. 48, 2007, pp. C741-C758. [6] Y. Kliafas and M. Holt, “LDV Measurements of a Tur- bulent Air-Solid Two-Phase Flow in a 90˚ Bend,” Ex- periments in Fluids, Vol. 5, No. 2, 1987, pp. 73-85. doi:10.1007/BF00776177 [7] K. A. Ibrahim, M. A. El-Kadi, M. H. Hamed and S. M. El-Behery, “Gas-Solid Two-Phase Flow in 90˚ Bend,” Alexandria Engineering Journal, Vol. 45, No. 4, 2006, pp. 417-433. [8] M. S. A. Bradley, “Understanding and Controlling Attri- tion and Wear in Pneumatic Conveying,” SHAPA Tech- nical Paper No. 5, April 2002. [9] Z. Tian, “Numerical Modeling of Turbulent Gas-Particle Flow and Its Applications,” PhD Thesis, School of Aero- space, RMIT University, Melbourne, 2006. [10] K. W. Chu and A. B. Yu, “Numerical Simulation of Complex Particle-Fluid Flows,” Powder Technology, Vol. 179, No. 3, 2008, pp. 104-114. doi:10.1016/j.powtec.2007.06.017 [11] X. Chen, B. S. McLaury and S. A, “Shirazi, Numerical and Experimental Investigation of the Relative Erosion Severity between Plugged Tees and Elbows in Dilute Gas-Solid Two-Phase Flow,” Wear, Vol. 261, No. 7-8, 2006, pp. 715-729. doi:10.1016/j.wear.2006.01.022 [12] T. Deng, A. R. Chaudhry, M Patel, I. Hutchings and M. S. A. Bradley, “Effect of Particle Concentration on Erosion Rate of Mild Steel Bends in a Pneumatic Conveyor,” Wear, Vol. 258, No. 1-4, 2005, pp. 480-487. doi:10.1016/j.wear.2004.08.001 [13] S. Dosanjh and J. A. C. Humphrey, “The Influence of Turbulence on Erosion by a Particle Laden Fluid Jet,” Wear, Vol. 102, No. 4, 1985, pp. 309-330. doi:10.1016/0043-1648(85)90175-9 [14] G. M. Faeth, “Mixing, Transport and Combustion in Sprays,” Progress in Energy and Combustion Science, Vol. 13, No. 4, 1987, pp. 293-345. doi:10.1016/0360-1285(87)90002-5 [15] AEA Technology Engineering Software Limited, Water- loo, Canada N2L 5Z4. Copyright © 2011 SciRes. EPE |

