The common physical origin of the glass transition, macromolecular entanglement and turbulence

doi:10.4236/ns.2011.37081

Paper Menu >>

Journal Menu >>

Vol.3, No.7, 580-593 (2011) Natural Science

http://dx.doi.org/10.4236/ns.2011.37081

The common physical origin of the glass transition,

macromolecular entanglement and turbulence

Jia-Lin Wu

College of Material Science and Engineering, Donghua University, Shanghai, China; *Corresponding Author: jlwu@dhu.edu.cn

Received 27 March 2011; revised 27 April 2011; accepted 3 May 2011.

ABSTRACT

The interface excitation (IE) on intermolecular

interface is a common concept connecting the

glass transition (GT), macromolecular entan-

glement (ME), and turbulence. IE has an addi-

tional repulsion energy and extra vacancy vol-

ume that result from the two neighboring mo-

lecules with antiparallel delocalization all in, e.g.,

the z-axial ground state of single-molecule in-

stantaneous polarized dipole at GT. IEs only

occur in the 8 orders of 2D IE loop-flows on lo-

cal x-y projection plane. Theoretical proof of the

3.4 power law of ME viscosity reveals that 1) the

delocalization mode of GT and solid-liquid tran-

sition is solitary wave; wave-particle duality of

solitary wave is ascribed to the equal probabili-

ties between appearing and disappearing of IE

loop-flow in inverse cascade and cascade mode;

2) macromolecular chain-length in ME motion

corresponds to Reynolds number in hydrody-

namics; both the ME motion and the turbulent

flow obey the same scale law. IE is not the ex-

citation of dipole energy level at GT. However,

when IEs are associated with the energy levels

of instantaneous polarized dipole, we predict

that the coherent structure formed by multilevel

8 orders of 2D IE loop-flows is the physical ori-

gin of turbulence based on the universal ran-

dom delocalization transition theory.

Keywords: Glass Transition; Mosaic Stricture;

Reptation; Coherent Structure; Random Transition

1. INTRODUCTION

Turbulence is well-deservedly often called as “the last

great unsolved problem of the classical physics.” Despite

enormous advances in sciences and many highly impor-

tant new scientific domains emerged in the past century,

the modern status of the turbulence theory is quite ex-

ceptional and differs from that of all other new sciences

[1]. On the other hand, Nobel laureate Philip Anderson

wrote, “The deepest and most interesting unsolved pro-

blem in solid state is probably the nature of glass and

glass transition (GT)” [2]. In physical theory, many

complicated phenomena originate from the global prop-

erties (Berry’s Phase) of simple quantum systems [3] and

the emergent properties of the many-times repeated ap-

plication of quite simple physical laws [4]. It is discov-

ered in this paper that the physical origin of turbulence is

the same as that of GT and macromolecular entangle-

ment (ME) when solving GT and ME in polymer phys-

ics. The three famous problems all attribute to the in-

corporation of many physical ingredients, containing the

maximal Berry’s phase  of interface excitation (IE)

loop-flows and the slowest also the maximum Brownian

regression-order potential in random systems. The ap-

pearance of the 8th order IE loop-flow plays the domi-

nant role in inducing molecule-cluster localization - de-

localization transition and flow speedup along one-di-

mensional direction in a reference 3D domain.

The minimum energy mode of the structure (confor-

mational) rearrangements in supercooled liquid could be

deduced from the motion mode of ME in melt liquid

state. This means that we can directly use the GT theory

(also proof-test the GT theory) to prove the 3.4 power

law of viscosity in ME [5,6], which is a well - known

experiment law found more than 60 years ago and yet

failing to have theoretical proof ever since. This power

law is theoretically proved in this paper. The real sur-

prise comes when we deduce the scale law of ME mo-

tion from the power law and find that the macromolecu-

lar chain-length corresponds to the Reynolds number in

hydrodynamics; both the ME motion and the turbulent

flow obey the same scale law. These findings indicate

that both ME and turbulence relate to the same theory

and the solid-to-liquid GT is the paradigm from disorder

to more disorder transition in inverse cascade – cascade

mode.

Very recently, Aleiner et al. [7] show theoretically that

the one-dimensional gas of short-range interacting ato-

mic bosons in the presence of disorder can undergo a

J.-L. Wu / Natural Science 3 (2011) 580-593

581

finite-temperature phase transition between two distinct

states: fluid and insulator, and the Anderson localization

- delocalization transition can be identified in the dy-

namics of expansion of disordered bosonic clouds re-

leased from the superimposed trapping potential. This

study may also provide an existent evidence for univer-

sal random delocalization transitions presented in this

paper, if we regard the energy of finite-temperature as

the Brownian directional regression vibration energy

along one-dimensional direction in a 3D local space and

the transition between two distinct states as the inverse

cascade—cascade mode of localization—delocalization

transition in random systems.

This paper is organized as follows. Section 2 reca-

pitulates the mosaic structure theory of GT, including the

fixed point of self-similar two-body interaction, frustra-

tion-percolation transition; and further proves the inverse

cascade – cascade mode is the fundamental mode of GT

via a validity check of GT theory for the well-known

abnormal exponential function in glass state. In Section

3, we unveil the structure of ME by means of the theo-

retical proof for the 3.4 power law of viscosity; and

show the theoretical contrast between random delocali-

zation transition and phase transition. In Section 4, we

present the theoretical predictions for the coherent struc-

ture of turbulence based on the universal geometric frus-

tration-percolation transition theory.

2. MOSAIC STRUCTURE

2.1. Inverse Cascade–Cascade Mode

One of the GT theories is the inverse cascade–cascade

mode along local one direction (e.g. notated in local

z-axial, or on x-y projection plane) in a reference (thaw,

excited) domain. The definition of excited domain in GT,

similar to that in a ferromagnetic material, is a contigu-

ous region in which the direction of thawing mole-

cule-cluster spontaneous delocalization (Section 3.3) is

uniform and different from that in neighboring regions.

This idea comes from the insight for cooperative orien-

tation activation energy, ΔEco, on melt high-speed spin-

ning-line [8]. When the work of the stress on over

5000 M/min spinning-line reaches ΔEco, the structure of

the yarn is stable and reaches full orientation, called as

FOY (Full Orientation Yarn) in current polyester fiber

industry. This phenomenon is called stress-induced GT.

The rate of change of the stress-induced liquid-to-solid

GT is 107 times of that in general quencher from melt

state to frozen glass state. A logical explanation for melt

high-speed spinning is that the macromolecules can

complete liquid-to-solid GT with full orientation within

the millisecond of time in z-space. Their motion mode,

within the entire range from melt transition (MT) tem-

perature Tm to GT temperature Tg, allows the direction of

inverse cascade – cascade in every excited domain is in

arbitrary in melt state and all apt to z-axial on melt spin-

ning-line; and finally the mode is frozen in glasses as the

soft matrix. At solid-to-liquid GT, increasing tempera-

ture only increases the number of IE loop-flows per unit

time to augment the number of thawing domains to ac-

celerate GT. According to the fundamental view and

central assumption of de Gennes’ soft matrix on mosaic

structures in glasses [9], an intrinsic 8 orders of transient

2D mosaic geometric structure theory of GT has been

proposed [10], Figure 1.

The structure is formed by the 8 orders of 2D IE loop-

flows from small to large in inverse cascade and rear-

rangement structure in cascade. The number of IEs on

the 8th order loop is identified by means of the geomet-

ric frustration, i.e., the appearance of the 8th order di-

rectly corresponds to that of boson peak and geometric

frustration in order to satisfy the claims for the theory of

GT [9-12]. The number of IE of the 8th order loop

equals to that of the 7th order, and the directions of the

two loops are opposite. Thus the 8 orders of 2D IE loop-

flows with one external degree of freedom (DoF) may be

also regarded as a domain-scale interacting classical

boson formed by 200 z-component chain-particles (mo-

lecules) [10] in a z-axial thaw domain. Furthermore, this

GT theory shows explicitly that the geometric frustration

also directly corresponds to the geometric frustration-

-percolation transition of the 8th order loop-flow to

balance the potential and the kinetic [10]. The centric 8th

order (V8) loop one by one connects with its neighboring

4 7th order (V7) loops in Figure 1. When the 4 V7 loops,

one by one, all evolve to their V8 loops (each V8 loop has

one external DoF); the central V8 loop obtains 5 inner

DoF and cascades to vanish (that is also the microscopic

melting mode with renewed cluster energy, kTm° (v8)).

This evolving picture holds true for all IE loops that

form the flow-percolation at the GT.

In Figure 1, each (small square) chain-particle has a

z-axial displacement energy 



that comes from the

Berry’s phase of parallel transports of its 4 IEs surround

its z-axis. The 8th order loop induces each of 136 parti-

cles to hop in z-axial respectively at different regression

times [10]. The central 5 cavity cells, in accordance with

de Gennes’ simple picture of “a localized ‘vacancy’

among clusters” [9], are also the mosaic cells denoting

the 5 cooperative excited particles [10] delocalized in the

correlation of sharing energy Ec (Section 3). This struc-

ture can deduce three non-integrable energies: kT2°,

kTg°, kTm° and an icosahedral directional ordering at

the GT.

The 8 orders of IE loop-flows also define the z-axial

self-similar 8 orders of transient 2D clusters vi (relaxa-

tion time



i) and 8 orders of transient 3D hard spheres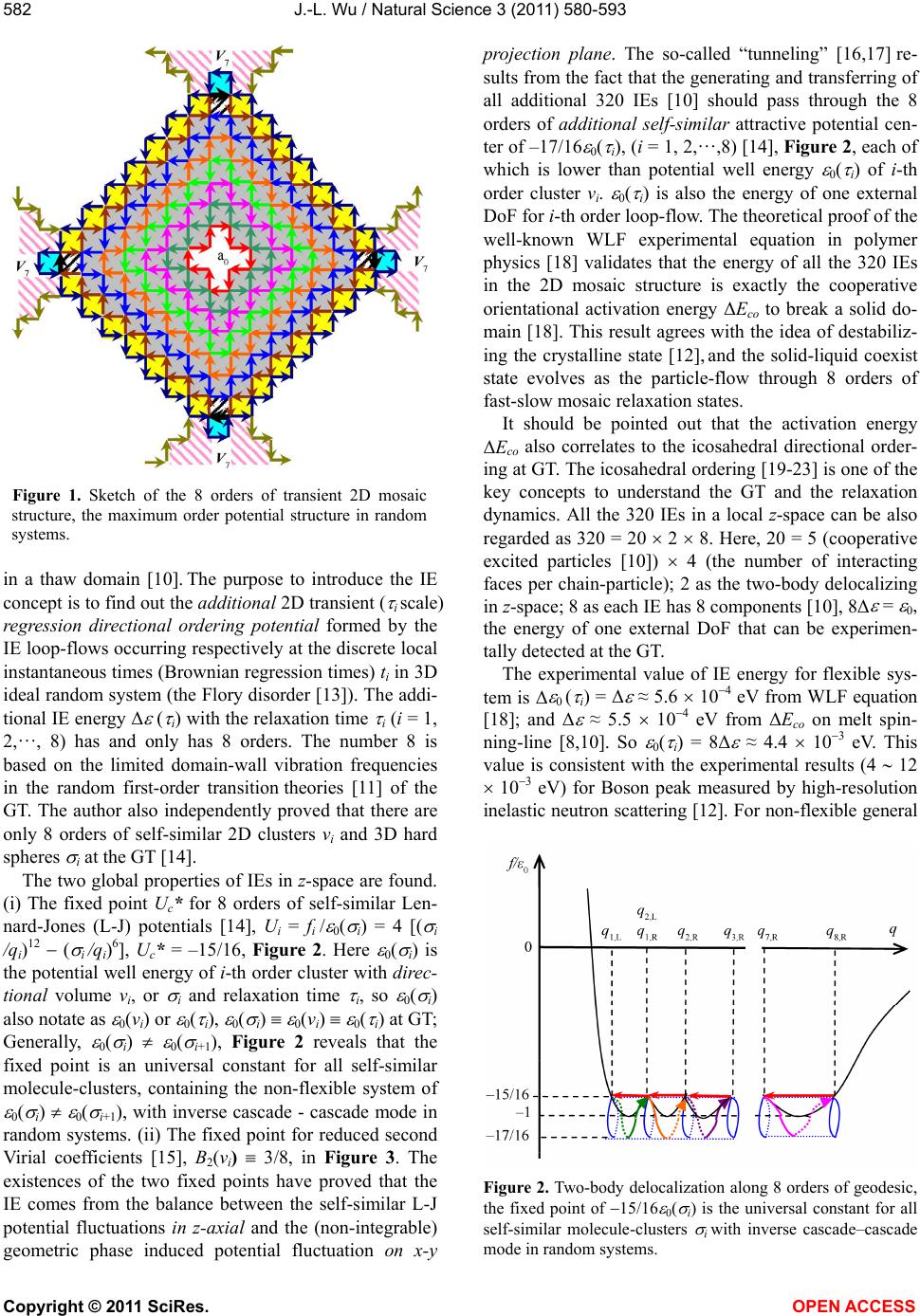



J.-L. Wu / Natural Science 3 (2011) 580-593

582

Figure 1. Sketch of the 8 orders of transient 2D mosaic

structure, the maximum order potential structure in random

systems.

in a thaw domain [10]. The purpose to introduce the IE

concept is to find out the additional 2D transient (



i scale)

regression directional ordering potential formed by the

IE loop-flows occurring respectively at the discrete local

instantaneous times (Brownian regression times) ti in 3D

ideal random system (the Flory disorder [13]). The addi-

tional IE energy Δ



(



i) with the relaxation time



i (i = 1,

2,…, 8) has and only has 8 orders. The number 8 is

based on the limited domain-wall vibration frequencies

in the random first-order transition theories [11] of the

GT. The author also independently proved that there are

only 8 orders of self-similar 2D clusters vi and 3D hard

spheres



i at the GT [14].

The two global properties of IEs in z-space are found.

(i) The fixed point Uc* for 8 orders of self-similar Len-

nard-Jones (L-J) potentials [14], Ui = fi /





i) = 4 [(



/qi)12  (



i /qi)6], Uc* = –15/16, Figure 2. Here





i) is

the potential well energy of i-th order cluster with direc-

tional volume vi, or



i and relaxation time



i, so





also notate as



0(vi) or





i),





i) 



0(vi) 





i) at GT;

Generally,





i) 





i+1), Figure 2 reveals that the

fixed point is an universal constant for all self-similar

molecule-clusters, containing the non-flexible system of





i) 





i+1), with inverse cascade - cascade mode in

random systems. (ii) The fixed point for reduced second

Virial coefficients [15], B2(vi)  3/8, in Figure 3. The

existences of the two fixed points have proved that the

IE comes from the balance between the self-similar L-J

potential fluctuations in z-axial and the (non-integrable)

geometric phase induced potential fluctuation on x-y

projection plane. The so-called “tunneling” [16,17] re-

sults from the fact that the generating and transferring of

all additional 320 IEs [10] should pass through the 8

orders of additional self-similar attractive potential cen-

ter of –17/16





i), (i = 1, 2,…,8) [14], Figure 2, each of

which is lower than potential well energy





i) of i-th

order cluster vi.





i) is also the energy of one external

DoF for i-th order loop-flow. The theoretical proof of the

well-known WLF experimental equation in polymer

physics [18] validates that the energy of all the 320 IEs

in the 2D mosaic structure is exactly the cooperative

orientational activation energy ΔEco to break a solid do-

main [18]. This result agrees with the idea of destabiliz-

ing the crystalline state [12], and the solid-liquid coexist

state evolves as the particle-flow through 8 orders of

fast-slow mosaic relaxation states.

It should be pointed out that the activation energy

ΔEco also correlates to the icosahedral directional order-

ing at GT. The icosahedral ordering [19-23] is one of the

key concepts to understand the GT and the relaxation

dynamics. All the 320 IEs in a local z-space can be also

regarded as 320 = 20  2  8. Here, 20 = 5 (cooperative

excited particles [10])  4 (the number of interacting

faces per chain-particle); 2 as the two-body delocalizing

in z-space; 8 as each IE has 8 components [10], 8Δ



the energy of one external DoF that can be experimen-

tally detected at the GT.

The experimental value of IE energy for flexible sys-

tem is Δ



0 (



i) = Δ



≈ 5.6  104 eV from WLF equation

[18]; and Δ



≈ 5.5  104 eV from ΔEco on melt spin-

ning-line [8,10]. So





i) = 8Δ



≈ 4.4  103 eV. This

value is consistent with the experimental results (4  12

 103 eV) for Boson peak measured by high-resolution

inelastic neutron scattering [12]. For non-flexible general

Figure 2. Two-body delocalization along 8 orders of geodesic,

the fixed point of 15/16





i) is the universal constant for all

self-similar molecule-clusters



i with inverse cascade–cascade

mode in random systems.

J.-L. Wu / Natural Science 3 (2011) 580-593

583

system, each of 320 IEs may have different IE energy.

Thus, each material has its own two inherent values of

independent of temperature in its own random system:

the geometric frustration—percolation (also the localiza-

tion—delocalization) transition energy, Ec = kTg° (vi),

and the renewed cluster energy, kTm°(vi). kTg°(vi) is also

the non-integrable directional regression vibration (DRV)

kinetic energy of i-th order cluster vi, kTg°(v8) = kTg in

inverse cascade; and kTm°(vi) = kTg°(vi) + 4



0(vi), kTm°(v8)

= kTm, of the 8 orders of clusters in cascade [10].

2.2. Origin of Interface Excitation in

Statistical Physics

This theory differs from current mode-coupling theo-

ries [11] of GT. A phenomenological concept of IE is

introduced by the ripplon and the universal Lindemann

distance increment [10] dL in order to obtain the global

properties of IEs in inverse cascade – cascade. The spirit

in mode-coupling scheme deals with the coupling of

fast-slow relaxation modes and two density modes in

structure rearrangements at GT. In our mode-coupling

scheme, we first focus on finding out the three direction

non-integrable energies kT2°, kTg° and kTm° existing in

the coordinates invalidation from i-th order clusters to (i

+ 1)-th order at GT, in spite of the time complications in

all anharmonic frequencies. This means that the crucial

2D 2 closed loop with the maximum non-integrable

Berry’s Phase plays a major role in anharmonic fre-

quency. The mode-coupling trick is that the relaxation

time complications have been beforehand reduced and

replaced by the slow Brownian directional regressions.

Then we deduce from global to local to find out the mi-

croscopic origin of IE (Section 2.3). The mosaic struc-

ture theory of GT reaches a new level by revealing the

microscopic physical origin of IE.

The fluctuation stability condition in (ii) is that the

chemical potentials are always zero in all subsystems

[15]. There is a profound theoretical contrast between

chemical potential and ‘temperature’. The chemical po-

tential is defined as Fermi energy level on the occasion

when the random kinetic energy of temperature in sys-

tem is zero in solid physics; whereas the non-integrable

random DRV energy, kTg°, in a thaw domain, is defined

as the delocalization energy, Ec, on the occasion when

the chemical potentials in all subsystems are always zero

at the solid-to-liquid GT. The key here is that the kTg is

only comprised by the slowest (z-space) DRV energy,

which is exactly the lowest-frequency (



i scale) mode

that has been explored at the GT. The x-axial and y-axial

(



i scale) DRV energy of all z-component molecules

(chain-particles) encircled by IEs should be zero in order

to minimize the total dominant GT energy.

In Figure 2, there are 8 sharp-angled points, U

c* =

U(qi,R) = U(qi+1, L) [14], forming the delocalization paths

of two z-axial (i.e. q-axial in the figure)



1 clusters along

8 orders of geodesic with IE energy 



(τi) = 1/8



0(τi).

i-th order geodesic is the shortest line of 2



cycle be-

tween qi,R and qi+1,R on i-th order of cylindric potential

surface (on x-y projection plane, taking



0 = 1 as

z-coordinate axis). The red arrows denote the paths of

structure rearrangements in cascade: from q8,R → q7,R

→ …→ q1,R → q0,R.

2.3. Absence of Attraction in 2D Lattices

Thus, two



1 clusters are in the delocalization state,

absent of attraction in vibration, along 8 orders of geo-

desic. The two molecule-clusters in the absence of Van

der Waals attraction are all through in a repulsion state

on the x-y projection plane during generating their one

IE. Van der Waals interaction includes the contribution

of instantaneous induced dipole - induced dipole.

Generally, instantaneous polarized dipole electron ch-

arges randomly distribute on interface 1-2 forming elec-

tron cloud (blue zone) in Figure 3(a).

At GT, an interesting and unexplored corner in Van

der Waals interaction theories is that the synchronal in-

stantaneous polarized electron charge coupling pair (two

small blue dots) may parallel transport on an interface

1-2 between chain-particles a0 and b0, or the interface

2-3 between a0 and c0 to form IE in Figure 3(b), or 3(c).

Since the site-phase difference on x-y plane between the

two z-component molecules is  [10], the state of the all

polarized electron charges in each instantaneous dipole,

in the two z-component molecules in Figure 3(b-1) or

3(c-1), must be in the same state and in the z-axial min-

imum energy state (ground state) of single-molecule in-

stantaneous dipole. In Figure 3, (b-2) and (c-2) is re-

spectively the projection of (b-1) and (c-1) on x-y plane.

Thus, the additional IE energy is the repulsive energy

between the two instantaneous synchrony z-axial ground

state polarized electron charges that parallel transport,

from one end to other end on an interface in Figure

3(b-2), simply denoted by an arrowhead (12) in 3(d)

on local x-y projection plane. Note that the two IE states

of (b-1) and (c-1) in Figure 3 occur at different local

instantaneous times. The directions of the next two par-

allel transports of instantaneous polarized electron

charge of the reference a0 are denoted as two red-broken

line arrowheads in Figure 3(c-1). IE loop-flow 1 2 

3  4 1 in Figure 3(d) offers a non-integrable poten-

tial 



to induce ion a0 (the center of mass of a0 particle)

z-direction a displacement z. Black-broken line arrow

denotes the delocalizing direction of each ion in Figure

3. Figure 3 explains the origin of 5-particle cooperative

excited field in [10]. The molecules in the absence of the

x-, y-axial (



i scale) vibrations are in the high density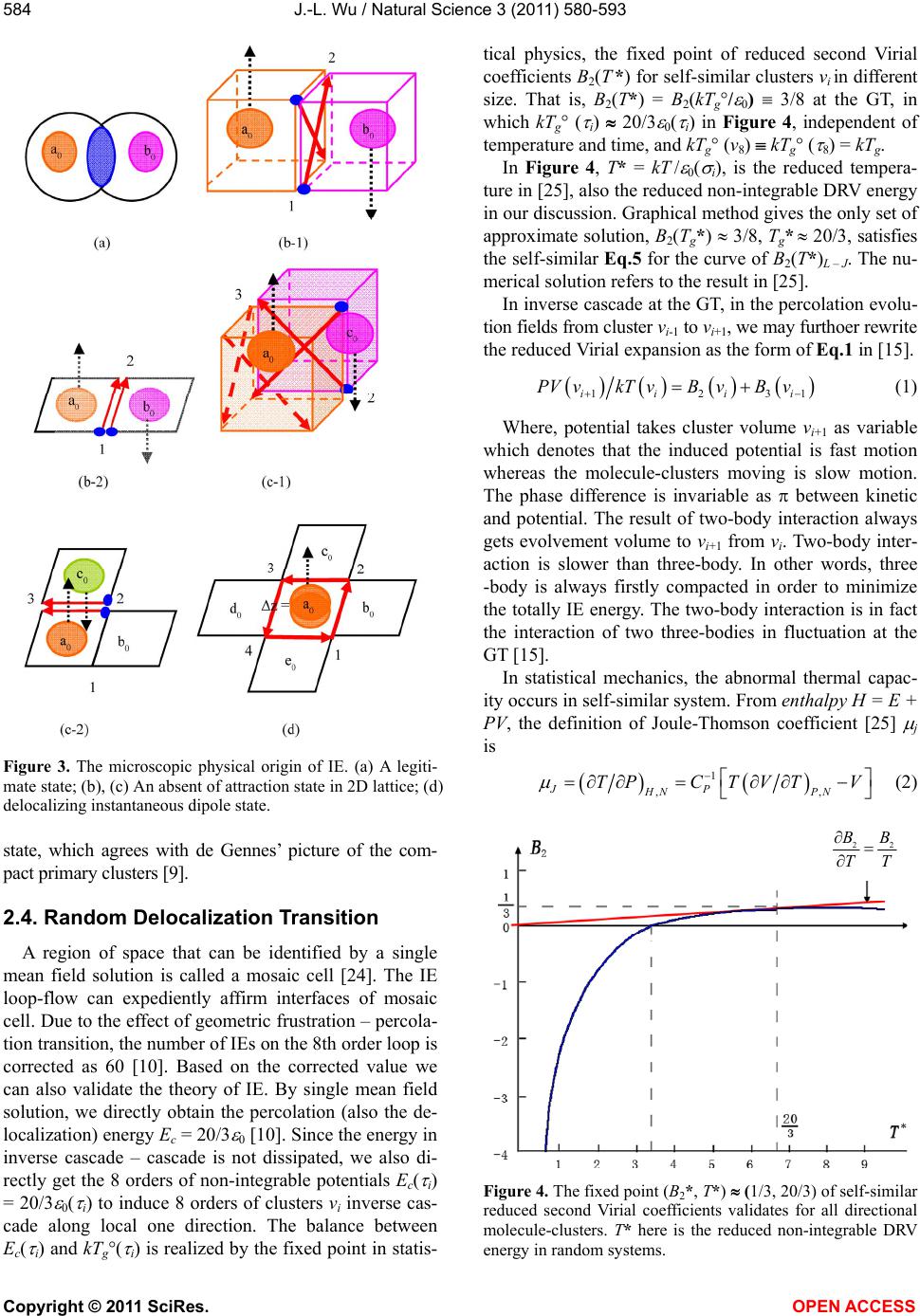

J.-L. Wu / Natural Science 3 (2011) 580-593

584

Figure 3. The microscopic physical origin of IE. (a) A legiti-

mate state; (b), (c) An absent of attraction state in 2D lattice; (d)

delocalizing instantaneous dipole state.

state, which agrees with de Gennes’ picture of the com-

pact primary clusters [9].

2.4. Random Delocalization Transition

A region of space that can be identified by a single

mean field solution is called a mosaic cell [24]. The IE

loop-flow can expediently affirm interfaces of mosaic

cell. Due to the effect of geometric frustration – percola-

tion transition, the number of IEs on the 8th order loop is

corrected as 60 [10]. Based on the corrected value we

can also validate the theory of IE. By single mean field

solution, we directly obtain the percolation (also the de-

localization) energy Ec = 20/3



0 [10]. Since the energy in

inverse cascade – cascade is not dissipated, we also di-

rectly get the 8 orders of non-integrable potentials Ec(



= 20/3





i) to induce 8 orders of clusters vi inverse cas-

cade along local one direction. The balance between

Ec(



i) and kTg(



i) is realized by the fixed point in statis-

tical physics, the fixed point of reduced second Virial

coefficients B2(T *) for self-similar clusters vi in different

size. That is, B2(T*) = B2(kTg°/



0)  3/8 at the GT, in

which kTg° (



i)  20/3





i) in Figure 4, independent of

temperature and time, and kTg° (v8)  kTg° (



8) = kTg.

In Figure 4, T* = kT /





i), is the reduced tempera-

ture in [25], also the reduced non-integrable DRV energy

in our discussion. Graphical method gives the only set of

approximate solution, B2(Tg*)  3/8, Tg*  20/3, satisfies

the self-similar Eq.5 for the curve of B2(T*)L – J. The nu-

merical solution refers to the result in [25].

In inverse cascade at the GT, in the percolation evolu-

tion fields from cluster vi-1 to vi+1, we may furthoer rewrite

the reduced Virial expansion as the form of Eq.1 in [15].







 

1231iiii

PV vkT vBvBv



 (1)

Where, potential takes cluster volume vi+1 as variable

which denotes that the induced potential is fast motion

whereas the molecule-clusters moving is slow motion.

The phase difference is invariable as  between kinetic

and potential. The result of two-body interaction always

gets evolvement volume to vi+1 from vi. Two-body inter-

action is slower than three-body. In other words, three

-body is always firstly compacted in order to minimize

the totally IE energy. The two-body interaction is in fact

the interaction of two three-bodies in fluctuation at the

GT [15].

In statistical mechanics, the abnormal thermal capac-

ity occurs in self-similar system. From enthalpy H = E +

PV, the definition of Joule-Thomson coefficient [25]



 

HN PN

TPCT VTV





 



(2)







Figure 4. The fixed point (B2*, T*)  (1/3, 20/3) of self-similar

reduced second Virial coefficients validates for all directional

molecule-clusters. T* here is the reduced non-integrable DRV

energy in random systems.

J.-L. Wu / Natural Science 3 (2011) 580-593

585

Assume the state of



J  0 corresponds to GT. When



J  0



,PN

VT VT (3)

Rewrite as Eq.4 for vi cluster

 





 

ii ii

Vv kTvVv kTv  (4)

Here kT in (2)  (4) should be also regarded as the

non-integrable random DRV energy of i-th order cluster

vi in z-space. The energy kT also is a function of the

self-similar cluster volume v

i, when outside pressure

(stress) remains constant. As long as the condition



J  0

in (2) is satisfied and (4) also holds, CP in the case of (4)

may also show an abnormal change. We see the abno r-

mal thermal capacity may occur in the following two

cases. One is in the polymer GT, CP occurs at the tem-

perature Tg. In this case, the kTg (= Ec) is the percolation

energy. The other is in the low-temperature GT in local

domain region, the abnormal thermal capacity occurs in

the manner of the energy of Boson Perk.

The hard-sphere (square well potential with IE energy)

model at the GT can be also deduced from the 8 orders

of self-similar L-J potentials along the clusters inverse

cascade direction [14]. It can be strictly proved that the

reduced third Virial coefficient for hard-sphere system is

constant, B3  5/8, [25,26] independent of temperature

and cluster volume. Thus, in z-space of the clusters in-

verse cascade, we can also get B3(vi-1)  5/8. Therefore,

in the percolation evolving field from cluster v

i-1 to v

from the interaction of two three-bodies, we have

  

2ii i

PV vkT vBv

in z-space fluctuation. In z-space, from (1),



 



22ii

iii

Bv Bv

Vv kTv Vv





From (4), we obtain an important self-similar Eq.5 at

the GT in [15].



22ii

Bv Bv

kTv kTv



 (5)

It Figure 4, if we regard the energy of T

g* as the

z-space reduced DRV kinetic energy of 8 orders of

self-similar clusters, the point (B2, kTg°)  (3/8, 20/3



is exactly the universal geometric frustration  percola-

tion transition energy for any cluster volume v in random

delocalization transitions. Moreover, the B2  3/8 at the

GT is directly proved by scaling theoretical approach [15].



  

23-1

3858 1

PV vBv Bv

kT v

  (6)

where i = 1, 2,…, 7, and when i = 8, the induced poten-

tial Ec directly equals to kTg in the geometric frustration

– percolation transition at GT. Eq.6 holds true on all

subsystems (flow-percolation fields), which means that

the kinetic energy always keeps balances with the poten-

tial energy, in the manner of the maximum Berry’s phase

of , in the mode of 8 orders of coupling 2body-3body

fluctuation clusters at GT.

2.5. Order-Induced Molecule Delocalization

The concept of connecting Anderson transition and

GT is the percolation limit model. In the theory of An-

derson disorder-induced (electron) localization [13], the

competition between kinetic energy and potential energy

influences on the electron states can reside in the ratio

W/B, W, the magnitude of the random potential, and B,

the (crystal) bandwidth in the absence of disorder. A

classical method of demonstrating consequences of dis-

order is the percolation model [13]. At the GT, the per-

colation transition energy is Ec(



8) = Ec. ΔEco is the ori-

entation activation energy with 320 IEs on the 8-order

2D mosaic structure in local z-space [10]. The ratio of Ec

/ΔEco 



c(Ec) 1/6, its physical meaning is that



c(Ec)

specifies the occupied fraction of z-space 320 IE states

that allow flow of energy Ec to occupy. The reason of the

cooperative molecules obtaining the probability of delo-

calization is that they share energy Ec. The ratio is con-

sistent with the result (the classical analog for electron

delocalization) of Zallen [13], who suggests



c (Ec) 

0.16  1/6, for the percolation limit on a continuum in

3D space. Here, the occupied fraction of all IE states

allowed to flow of energy Ec, takes the place of the oc-

cupied fraction of space allowed to molecules of energy

Ec. This means that there is the inherent theoretical con-

trast between molecule delocalization and electron lo-

calization on the concept of percolation limit.

That is, from the viewpoint of percolation, there are

two classical percolation limits. One is the limit of the

maximum disord er for the potential in random corre-

sponds to the Anderson transition, that is the Zallen’s

viewpoint [13]; whereas, the other is the limit of the

maximum order for the potential in random to the GT. At

the GT, all molecules encircled by 4 IEs on x-y projec-

tion plane are in the minimum excited energy state

(states), i.e., at the z-axial ground state of single - mole-

cule dipole in the absence of x-, y-axial (



i scale) vibra-

tions. The DRV induced potential energy in 5-particle

cooperative excited field [10] can be also regarded as the

overall order potential limit (in contrast to the maximum

disorder potential limit in Anderson random) in the ran-

dom Brownian motion. That is the reason we call the GT

as the order-induced molecule (molecule-cluster) delo-

calization transition in random systems.

In other words, the delocalization energy Ec at the GT

J.-L. Wu / Natural Science 3 (2011) 580-593

586

comes from the maximum order energy in random and

the minimum additional ground-state repulsive energy.

Thus, the percolation limit mode (the crossover from the

site- or bond- percolation in solid to the flow-percolation

in liquid) of the GT can probably explain why the 8 or-

ders of 2D mosaic geometric structure (Figure 1) asso-

ciated with percolation transition so simple. That is, this

nano-scale soft mosaic structure reflects the nature of

random delocalization transition in random systems.

2.6. Percolation Limit Picture at GT

The theory of IE loop-flow directly and definitely

shows Emig = kT2 = 17/3



0. Emig is defined as the average

energy of cooperative migration along one direction in a

percolation field [10], independent of temperature. Dur-

ing [ti, ti + ti] in a reference domain, the entire transient



i scale displacement energy in  z-axial is (136/8)



0 =



0, Figure 1, and the



i scale vibration energy in x-,

y-axial is zero; thus, the average DRV kinetic energy is

also 17/3



0 = kT2. On the other hand, during (ti + ti, ti+1),

the average random energy in the domain is as kT2.

However, the average DRV kinetic energy would occur

in other domains in the system during (ti + ti, ti+1) in the

reference domain at the GT. This is the dual-role of kT2

in kTg, reflecting the balance between random DRV en-

ergy and random thermal motion energy at the condition

of kTg°. If take Emig = kT2 as the average DRV kinetic

energy in dual-role, kT2 is in fact the deferred action

DRV kinetic energy until the appearance of the 8th order

2D loop (the appearance of kTg). In this case, kT2 will be

of the DRV kinetic energy of the 8th order cluster in the

absent of energy





8) in an excited domain in Figure 1.

Vice versa, when the temperature is T2, the reference

domain will also be of the probability of regression order

potential of kT2 if the domain can obtain the energy





8). Thus, the physical meaning of kT2 is that in a 3D

solid-domain, taking any reference direction, as long as

superadded the energy





8) on the domain, the sponta-

neous molecules delocalization would be occur in the

reference direction.

Its singularity different from phase transition is the

non-ergodicity that the adding energy may be either a

few energies only on several domains, or a large energies

one by one on neighboring domains to form a flow-

-percolation field. In any case, if the adding energy



denoted by temperature, it always satisfies kT2 +



0 = kTg.

In other words, here



0 =





8) is a reduced energy to

reduce the magnitude of its action region or its action

time in the system. The noticeable contrast between

phase transition and random transition in physical the-

ory (Table 1) is as follow. At Curie temperature point,

kTc, in magnetism, so as decrease a little of rando m en-

ergy (kT) in whole system, the spontaneous magnetiza-

tion will occur along one direction in whole system.

Whereas, at kT2 of the GT, so as increas e a little of di-

rectional ordering energy



0 in a local region, the mole-

cules spontaneous delocalization will occur along the

direction in the local region. It is in this sense T2 corre-

sponds to Curie temperature in magnetism. The numeri-

cal value of 17/3



0 is also validated by the WLF experi-

mental equation [18], 17/3



0 +



0 = kTg = 20/3



0 = Ec.

There are two critical delocalization energies Ec and kT2.

Ec is the critical percolation transition energy, corre-

sponding to the spontaneous delocalized solitary wave

(Section 3) in percolation field (the “ocean” in percola-

tion theory) at GT; and kT2 is the critical energy of parti-

cle-clusters delocalization at low-temperature GT in lo-

cal domain scale (the “lake” in percolation theory) in

percolation limit model. This percolation limit picture

with separate ‘lakes’ and ‘ocean’ is distinctly different

from the general percolation model. Note: the delocaliz-

ing step-size in glassy is far less than the amplitude of

thermal vibration, Section 3.3, thus the glass state in

random delocalizing is still in stable state.

2.7. Soft Matrix and Emergent Property

The de Gennes’ central assumption of the soft matrix

[9] is also validated. The soft matrix is exactly i-th (i  7)

order 2D loop-flows frozen in glass state. From which

the low-temperature GT would occur through a longer

Brownian regression time to inverse cascade until the

8th order and to cascade at low-temperature. The lower

the frozen, the longer is the required time of inverse

cascade. Therefore, the abnormal exponential function

[27] in glass state can be proved directly.

Generally, the physical quantity



(t) in a system will

return according to the physical law of Eq.7 when the

system deviates from its equilibrium state.



~exp t

















(7)

However, if the glassy system is driven (or normally

fluctuates) out of equilibrium, it returns according to the

formula [28]

exp t





























Where t is the (system) time and



and



are parame-

ters. Unfortunately this is not a mathematical expression

that is frequently encountered in physics. So little idea

exists of what the underlying mechanisms are [28].

Since the inverse cascade–cascade motions only occur

in some discrete “lakes” in glass state when T  Tg. Eq.7

still holds true in these “lakes” regions as long as the t in

(7) is the local domain time. One of the key concepts is

J.-L. Wu / Natural Science 3 (2011) 580-593

587

that the equilibrium state of glass state is the equilibrium

state between the random thermo motion energy kT and

the slowest DRV energy. DRV energy always dominates

the number of the excited domains at temperature T.

Assume the glass state we observed is the nonequilib-

rium state that comes from the equilibrium state at the

temperature T1 suddenly drops to the temperature T2 at

the time t = 0, and T2  T1  Tg. During the relaxation

time of t, the entire DRV relaxation energy is



= k(T1 

T2) = kT. From the famous Kolmogorov law in cascade

[1,29]

3constant

kTt



 

. (8)

Where li is the length scale of i-th order of loop (clus-

ter) and i



 is the cascade energy mobility; ti is the local

domain time and t is the relaxation time in system. From

(8)







 (9)

Substituting ti in (9) for t of local domain time in the

right term on (7)



~exp exp

loc



























 (10)

The physical meaning of



is very definitude,



=1/3

denotes the cascade motion in ideal glass state in the

case of the small fluctuation value of kT. The reason of

the deviation from 1/3 for



may be that (a) the influence

of the competition between the change ratio of tempera-

ture dT/dt and the 8 orders of relaxation times on IEs; (b)

the larger value of kT conduces



augment because of

the inverse cascade always lower than cascade. Similarly,

if the nonequilibrium glass state is arose by outside

stress (or electromagnetism and other factors) work W,

the relaxation of W can only realize through the inverse

cascade – cascade in the excited domains as same as that

in the proof of WLF equation [18]. In this case, we only

need replace kT by W in (9). This means that the ab-

normal mathematical expression (10) in glass state is

also only the emergent property of domains in system, as

same as the abnormal expression of WLF equation in the

GT (the many-times repeated applications of Clape-

yron equation governing first order phase transition on

the subsystems will educe WLF equation) [18]. The

general physical relaxation law (7) still holds true in

domain scale in glass state. The theoretical proof also

confirms that inverse cascade–cascade mode is the fun-

damental mode for glass state.

3. ENTANGLEMENT STRUCTURE

3.1. Theoretical Proof of the 3.4 Power

Law

The viscosity in ME melt is



 N3.4 for all linear en-

tangled polymers. Since N is a large number, the ex-

perimental 3.4 power law of viscosity has sensitivity for

any modified theory to de Gennes reptation model. In

concordance with the experimental 3.4 power law of

viscosity, within the experimental error range of viscos-

ity, we first roughly estimate the theoretical error toler-

ance by adopting a fine theory described ME viscosity.

The critical entanglement chain length Nc = 200 [11,30].

The experimental value of chain length N is generally

less than 103 (seeing the Fig. 9.5 in [5]). If taking the

range of N as 200  1000, N3.4 /N3.3  1.7 (N = 200)  2

(N = 1000). This indicates the error between theoretical

value and experimental result of viscosity will be about

70%  100% if the theoretical value as 3.3; and N3.4/

N3.35  1.3  1.4. This means that a fine theory should be

able to give the theoretical exponential value range of

viscosity as 3.4  0.05 for flexible polymers. At the same

time, we expect this theory must also be able to predict

the exponential of viscosity that is in line with the ex-

perimental results for non-flexible polymers. This is also

a fine way to check up the GT theory. The existing vari-

ous modified theories [5] cannot match for the 3.4 power

law. This exponent is significantly large than the predic-

tion of 3 by de Gennes reptation model [5,30] based on

the assumption that the chain of length N is a “free

chain”. The reason of the deviation is the required num-

ber of DoF of one-step-walk along z-axial for each chain

particle depends on Nz the z-component of chain N. The

key of the theoretical proof is to find out the number of

DoF, N*, for chain-length N. Only through substitution of

the reference chain of length N in single-chain reptation

model with an equivalent particle-chain of length N*, can

the random diffuse motion of the reference chain N be

entirely free in tube model. Thus, in the ‘equivalent mul-

tichain’ de Gennes reptation model, we have





 (11)

The one-step-walk along +z-axial of a reference parti-

cle a0 on chain Nz results from the induced action of the

8 orders of 2D loop-flows on the x-y projection plane in

a0 (local excited) field. Only when the 8th order appears

and acts on the particle a0, should one “particle-cavity”

in +z-direction appear in a0 field and bring a0 to move

one step along +z-axial. Statistically, when Nz  Nc = 200

(Nc is also the number of the chain-particles of structure

rearrangements [10,11,30,31] in the 8 orders of 2D mo-

saic structure), the moving of the 200 cooperative parti-

cles along z-space on x-y projection plane in a0 field

J.-L. Wu / Natural Science 3 (2011) 580-593

588

should share the energy Ec with a0. Due to the sharing

energy effect, even if a0 has obtained a cavity with

one-step-walk, the motion of a0 should still be correlated

with the 200 particles (molecules) in shared energy Ec.

In other words, the cooperative particles still “drag” the

one-step-walk of a0.

The external DoF of the 8th order 2D loop-flow en-

circled a0 is 1, taking





8) as the energy unit of DoF. In

order to eliminate the correlation of share energy to

make a0 move freely in z-axial, let Ec /





8) = Lg, where

Lg is the equivalent number of particles. Ec thus is as the

“loop-flow” energy with an equivalent chain of length Lg

circling a0. On the one hand, from the viewpoint of par-

ticle a0 on chain Nz, statistically, the Nc chain-particles

on Nz also share the energy Ec. Thus, the probability that

a0 is possessed of one unit DoF on the chain Nz is 1/N.

On the other hand, from the viewpoint of the Lg equiva-

lent particles, statistically, each equivalent particle is

located at its own long-chain with length Nz, and the

probability that each equivalent particle is possessed of

one unit DoF on its own long-chain is also 1/N.

When particle a0 on chain Nz is substituted by an

equivalent chain of length Lg, the probability of the event

that it obtains one unit DoF and freely moves one step

along z-axial, denoted as p+(a0). p+(a0) is namely the

probability of the event that all the Lg equivalent parti-

cles simultaneity move one step along z-direction in the

co-Brownian motion by 200Nz chain-particles in a0 field.

So, p+(a0) is given as



pa N

 (12)

Statistically, the probability of each particle freely

moving one step in z-space should be all equal to p+(a0).

To maintain the balance of motion between inverse cas-

cade and cascade in z-space, the probability that one

reference 8th 2D loop-flow disappears in cascade in

co-Brownian motion by 200Nz chain-particles is denoted

as p(a0) and obtained as follows.

Let a0 have nz DoFs with





8) as the unit in cascade

motion. nz is actually the number of DoF to make con-

formational rearrangement of the chain Nz in z-space,

which results from the contribution of the reference 8th

order 2D loop-flow transferred from the particle a0 field

to the other particle field on the chain. Similar to (12),

we have



pan

 (13)

where Lm = kTm /





8), Lm is the number of ‘equivalent

particles’ to eliminate the reference 8th order 2D

loop-flow of a0 in cascade.

In the complex inverse cascade–cascade motion, the

equilibrium condition is





pa pap



 (14)

so,







 (15)

The number of DoF of Nz chain-particles on chain of

length Nz to make conformational rearrangement in

z-space is Nz

*, Nz

* = nz Nz,









 (16)

In (16), Tg° has been approximately replaced by Tg.





8)  H, here H is enthalpy in (2), the constant en-

ergy for rearrange conformation (that also the energy of

z-space solitary wave in Section 3.3) in random system.

So, during the reptation of long-chain N in the 3D space,

the number of DoF Nx

* in the x-space and Ny

* in the

y-space have Nz

* = Ny

* = Nx

*, or









 (17)

From (11) and (17), we obtain the general power law

expression of viscosity in ME











 (18)

For flexible chain polymers, kTm = kTg + 4





8), kTg =

20/3





8) [10]. We have

NN (19)

And

83.375 3.4

ηNN N

This theoretical result conforms well with the experi-

mental data. For non-flexible chain polymer, Eq.18 can

be verified. For example, for the polypropylene (PP), the

Tg(PP) is 10C = 263k [32]; the Tm(PP) is 176C =

449k [33]; Eq.18 given



pp(theory)  N3.73, conforms

well with the experimental data



pp(experiment)  N3.72

[34].

The theoretical proof further confirms that inverse

cascade–cascade mode is the fundamental mode in the

solid-to-liquid transition whether in macromolecular or

in small molecular.

3.2. Degrees of Freedom of Chain-Length N

Since cascade is also the mode in turbulent flow, we

discuss the total number of DoF, NL, in the cube with

edge length of L (L  N*) in ME melts. The unit for the

length of L here is the loop scale, ls, of the 8th order 2D

loop-flow. Due to the properties of flow-percolation [10],

an 8th order 2D loop-flow may be in arbitrary direction.

In other words, in 3D space, we can consider any one

J.-L. Wu / Natural Science 3 (2011) 580-593

589

“random-walk chain” with “chain-length” NL and each

“chain-particle” with one unit length l

s. If the “end-to-

-end distance” of the “random-walk chain” is always

equal to L, L is then the root-mean-square of end-to-end

“chain-length” NL, that is, NL = L2, in Figure 5.

When L  N*, NL  (N*)2, from (19), we have

NN (20)

Comparing to the famous Kolmogorov relationship

[29] between the number of DoF NR and the Reynolds

numbers Re in (a uniform grid) turbulence

(21)

It can be seen that the two terms in two different sub-

jects: turbulence and ME both describe the same com-

plex motion phenomena about inverse cascade – cascade.

Both of them obey the same scaling law, which indicates

there is a universal theory behind them. Reynolds num-

ber is actually the ratio of the inertia force to the drag

force, and the macromolecular chain-length reflects the

ratio of the number of the particles “inertially” one by

one sharing the delocalization energy Ec to the one parti-

cle entangled with them in motion.

3.3. Solitary Wave

Each physical quantity in (12)  (18) is the inherent

invariable in random system for every material, inde-

pendent of temperature and time. Eqs.15 and 16 reveal a

z-space solitary wave moving N

z steps along a random

long-chain Nz from one end to other end. A distinct cha-

racteristic of the solitary wave is that the “particle” en-

ergy of each one-step-walk is “quantized”: nz





i) = nz



for flexible system. While nz





i) generally have 8 or-

ders of components, 8 orders of potential well energies

for general non-flexible system. The step-size is only the

nz particles of size. The number of step of its traveling

wave is Nz = N. The reptation in 3D space of a ME chain

is assembled in time by the three solitary waves on the

chain in x-, y- and z-space, which in fact attributes to the

co-Brownian regression motion by 200N chain-particles

respectively in x-, y- and z-space.

Accordingly, the ME structure about viscosity is in

fact the 8 orders of transient 2D mosaic structures on x-y

projection plane and the delocalized solitary wave in

z-space. nz is a small numerical value, e.g. if taking N =

Nc = 200, nz  0.036. However, Eq.15 reveals that nz

connects with the length-boundaries Nz of solitary wave

in its each one-step-walk. The velocity of traveling wave

will be determined by other factors including, e.g., the

generating ratio of IEs by temperature, time or outside

stress work, and the magnitudes of material relaxation

times in IEs. This special characteristic of solitary wave

shows that it differs from the mode of conventional quan-

Figure 5. The relationship between “chain-length” NL

and number of degrees of freedom.

tum-mechanical wave; the latter is always obtained from

the combination of both the wave equation and the bou-

ndary conditions.

3.4. Spontaneous Symmetry Breaking at GT

The paradigm for the phase transition theory is the

ferromagnetic transition. de Gennes [30] emphasized

that polymer solutions should compare with magnets.

However, difficulty occurs in the order parameter for a

polymer solution [30]. de Gennes proposed that the or-

der parameter is the magnetization of a spin system with

a number of spin components n = 0 [30]. Edwards’ more

concrete statement is that the order parameter



is simi-

lar to a quantum mechanical creation (or destruction)

operator [30]. The proof for 3.4 power law predicts a

definitude result for the remaining problem that the order

parameter is the spontaneous delocalized solitary wave



of a classical spin system (8 orders of 2D IE loops)

with a number of additional instantaneous spin compo-

nents n = 0, whether in macromolecules or in small

molecules, within the entire range from solid to liquid

transition. The physical meaning of n = 0 is here that the

additional “spin” of a reference chain-particle only

comes from the contributions of its 4 neighbouring par-

ticle fields, instead of its own inner-rotation change. In

addition, n = 0 also corresponding to self-avoiding ran-

dom walk [30] of 8th order 2D loop-flows.

Contrary to phase transition, we have unveiled the

step by step way from disorder to more disorder in Table

1. In which we have implied that the disordered degree

(measurement) depends on the maximum 2D IE

loop-size and the number of the loops in a random sys-

tem. The conjugate variables of solid-to-liquid transition

in Table 1 are deduced from the results of de Gennes in

[30].

J.-L. Wu / Natural Science 3 (2011) 580-593

590

Table 1. The contrast between delocalization transition and phase transition in 3D space.

Critical point Ferromagnetic phase transition Solid-to-liquid delocalization transition

Number of spin components n n = 3 n = 0

Cell Magnetic moment S displacement energy 



circled by 4 IEs

Spontaneity Magnetization M Delocalizing solitary wave



“Curie” point Tc kT2: critical delocalization energy

Reduced energy increment



= k (T



Tc) / kTc ,



 0, M = 0 in system



 0, M = S  0 in system



= k(T



T2) /



0: potential well energy



= 1, GT:



 0 in subsystems



 1, Low-temperate GT:



 0 in domain



= 5, MT: Reptation in subsystems

1



 5, Viscoelasticity (Intermittency)

Symmetry breaking M chooses one-space, breaking the isotropic M

GT: Solitary wave chooses one space, breaking the

isotropic thermal motion

MT: Three solitary waves in x, y, z-space restore the

isotropic thermal motion

Self-similar cluster cluster size



v   Finite 8th order cluster

Correlation length



 



=Nz, macromolecular chain-length



=Nc, for small molecule systems

Order parameter M Solitary wave



Replica symmetry Spin wave 8 orders of 2D IE loop-flows

Conjugate variables Extensive

quantity Intensive quantity

Nz (or Nc), step number of solitary wave



0, one-step-energy of solitary wave

Generalized rigidity Magnetic hysteresis 8th order 2D IE loop

Defect Domain boundary Extra vacancy volume in each IE on 8th order loop

4. COHERENT STRUCTURE

4.1. The Way to Turbulence

Thus, we have ascribed the GT problem to the syste-

matics of the special parallel transport state of bonding

on intermolecular interface. This is precisely in line with

the insight in [28] that crucial to the endeavor of GT

theory is a deeper understanding of the systematics of

bonding in condensed matter within a framework going

considerable beyond the current GT picture. All that we

have done is to replace the GT problem by the bonding

problem of parallel transport of instantaneous polarized

electron charges containing all atoms (atom-clusters) in

a chain-particle at the GT. However, we have progressed

and can now discuss turbulence.

The IE and the 8 orders of 2D mosaic structures at GT

may be called as the ground state IE and the first level of

8 orders of 2D mosaic structures. For small molecule

system, due to the energy transfer of rearrangement

conformation between two z-axial connecting molecules,

Nc z-component molecules respectively in absence of x-,

y-axial vibrations can also be connected one by one to

form a z-space random “long-chain with chain-section as

a molecule” walking Nc steps in the correlation of shar-

ing energy Ec.

Solid-to-liquid transition does not invoke the energy

level of molecule (molecule-cluster) instantaneous in-

duced dipole. However, for each energy level of mole-

cule (molecule-cluster) instantaneous polarized dipole,

e.g., for the first energy level of instantaneous polarized

electron charges of molecule (of all atoms and molecules

in a molecule-cluster), two neighboring molecules with

antiparallel delocalization may be all in the z-axial first

energy level state of single-molecule instantaneous po-

larized electron charges on an intermolecular interface.

Such IE is named as the first-energy-level IE. A new 8

orders of 2D mosaic structure can be formed, which is

called the second level of 8 orders of 2D coherent (mo-

saic) structure.

For small molecule liquid, only about 4/15 (8kTm /

Eco = 4/15) interfaces have been excited. As disorder

increases, more ground state IE will be excited to accel-

erate liquid flow, which corresponds to the ordinary flow

development.

As disorder keeps increasing and flow continues

speedup, each ground state IE on the 8th order 2D loop

can update to be the first-energy-level IE with new 8

orders of relaxation times, new additional IE energy and

vacancy volume. All other IEs on x-y projection plane

are still in the ground state of IE. All these z-component

molecules in the absence of x-, y-axial vibrations can

form a z-space random “long-chain” with “chain-section”

as 136 molecules encircled by 60 first-energy-level IEs.

J.-L. Wu / Natural Science 3 (2011) 580-593

591

60 first-energy-level IEs can form a 0-th “cluster-par-

ticle” in z-space in the second level of 8 orders of 2D

loop-flow, denoted as v0

(1) (a0), the figure in the super-

script parentheses denotes the first-energy-level IE of

single-molecule polarized electron charges. The 0-th

“cluster-particle” is self-similar to the z-component mo-

lecule a0 [named as v0(a0)] in Figure 1. The size of the

0-th “cluster-particle” is that of the 8th order cluster

v8(a0) in the first level of mosaic structures. The 0-th

“cluster-particle” has also 4 “interfaces” with the side

length of 15 IEs (one thick-black inverted arrow plus the

14 sky-blue arrows in Figure 1) of the first energy level.

Thus, the second level of 8 orders of 2D mosaic struc-

tures is self-similar to the first level. To drive the 136

molecules cooperatively move one step along +z-space

only needs the energy nz

(1)



(1). The mode is the solitary

wave with the first-energy-level IE in z-space.

4.2. Multilevel of Random Localization -

Delocalization Transitions

Inverse cascade is the accumulation of the directional

Brownian regression potential energy in loop-flows, and

cascade is the transfer of energy from potential to kinetic

to drive liquid cluster flow. The larger loop is formed in

inverse cascade, the bigger liquid cluster is driven in

cascade, and the higher efficiency the system has to ex-

cite liquid flowing, and the faster the velocity of flow is.

In the same way, when the flow keeps on speedup, the

third, the forth…the l-th level of 8 orders of 2D coherent

structures can be constructed one by one, in order to

augment the loop scale and the loop-potential so that the

maximu m 2D loop-potential reaches the value of the

potential forced by environment to the liquid flow. At the

moment, the l-th level geometric frustration – percola-

tion transition (seeing the universal pictures of Figures 1

and 2) appears and reaches potential balances with ki-

netic, and the cascade phenomenon of the maximum

loop-flow begins. This is the turbulent flow. The origin

of the intermittency turbulence [35] is that the high

non-ergodic state of flowing arises suddenly to make the

reduced energy increment,



(l), of each level with a value

slightly more than 1, similar to the viscoelasticity in Ta-

ble 1. The heteroclinic orbits [36] in turbulence may be

the flow-lattice edges of the l-th level 2D coherent struc-

tures.

The complicated turbulence can come down to the l-th

level solitary wave in z-space and the l  1 reptations

(snake-walks) of l  1 various levels (self-similar sub-

systems) simultaneously occurring in 3D space.

At critical phase transition, the self-similar cluster size



v  , while it is only Nc in GT, Table 1, which is

also the localization-delocalization scale of the first level

in universal random delocalization transitions. In other

words, on the way from disorder to more disorder, the

cluster size of



v   in critical phase transition will be

here divided up by l levels, Nc

(l), corresponding to the

cooperative localization – delocalization scale of l-th

level, i.e. it is also divided into l levels of geometric fru-

stration—percolation transitions, similar to Figures 1-5,

in random localization—delocalization transitions on the

way from disorder to more disorder. This is the way to

turbulence.

5. CONCLUSIONS

A theoretical perspective on the mosaic structure the-

ory of GT has been proposed. The theoretical approach

of GT connects closely the origin of turbulence. A new

and central concept is the instantaneous parallel trans-

port repulsive state absent of attraction in 2D lattices in

current Van der Waals interaction theories. The solid to

liquid GT is the paradigm of the inverse cascade – cas-

cade mode and the first level of the way to disorder and

turbulence. Nine physical ingredients, random, self-

similar, two-body interaction, fluctuation, frustration,

percolation, delocalization, Berry’s phase (parallel trans-

port) and Brownian regression potential, have been in-

corporated on IE loop-flows at the GT and the universal

random delocalization transition.

The theoretical proofs for the abnormal exponential

function in glass state and the 3.4 power law of viscosity

confirm that the inverse cascade–cascade mode is the

fundamental mode whether in solid to liquid transition or

in macromolecular motion. Due to the effect of incorpo-

ration of physical ingredients, the different terms in dif-

ferent subjects have been also incorporated. The inverse

cascade–cascade mode with mosaic structure reflects the

confluence of both the kinetic dimensions and the ther-

modynamics at the GT. It can be also denoted by both

the delocalization solitary wave (that is also the melt

mode, the conformational rearrangement mode, structure

rearrangement mode) along a local one-dimensional di-

rection and the 8 orders of 2D IE loop-flows (its scale or

size is also a domain scale, cage scale, local scale, cor-

relation scale of two-body interaction, random localiza-

tion-delocalization transition scale, maximum step-scale

of random walk, geometric frustration scale and critical

percolation scale in random systems) on the local pro-

jection plane.

Three different structure terms, the mosaic structure in

GT, the entanglement structure in ME and the coherent

structure in turbulence, are all in fact the transient 2D

geometric structure formed by IE loop-flows in their

own random system. The most important physical quan-

tity correlating GT, ME and turbulence is the directional

ordering induced potential of a maximum 2D IE loop-

flow in random system. Once the loop-flow is formed,

J.-L. Wu / Natural Science 3 (2011) 580-593

592

the GT appears, the critical ME phenomenon arises, and

the cascade in turbulence begins.

6. ACKNOWLEDGEMENTS

The author is grateful to all colleagues he had the pleasure to col-

laborate and interact, especially when he found the fundamental phys-

ics origin for the orientation activation energy obtained experimentally

on melt high- speed spinning-line in 1986. In particular, the author

would like to thank, in random order, Yuan Tseh Lee and Sheng Hsien

Lin of Academia Sinica (Taiwan), Yun Huang of Beijing University,

Da- -Cheng Wu of Sichuan University for useful discussions. Support

from the Academia Sinica (Taiwan), and the State Key Lab of Chemi-

cal Fibers and Polymer Materials, Donghua University (Shanghai) is

gratefully acknowledged.

REFERENCES

[1] Lesieur, M., Yaglom, A. and David, F. (2002) The trends

of turbulence. Springer, Berlin.

[2] Anderson, P.W. (1995) Through the Glass Lightly.

Scence, 267, 1615-1616.

doi:10.1126/science.267.5204.1615-e

[3] Berry, M.V. (1998) Foreword to “Global properties of

simple quantum systems—Berry’s phase and others”.

http://www.phy.bris.ac.uk.

[4] Kadanoff, L.P. (1991) Complex Structures from Simple

Systems. Physics Today, 44, 9. doi:10.1063/1.2810017

[5] Rubinstein, M. and Colby, R.H. (2003) Polymer physics.

New York Publisher, Oxford.

[6] Doi, M. and Edwards S.F. (1988) The theory of polymer

dynamics. New York Publisher, Oxford.

[7] Aleiner, I.L., Altshuler, B.L. and Shlyapnikov, G.V. (2010)

A finite-temperature phase transition for disordered

weakly interacting bosons in one dimension. Nature

Physics, 6, 900-904. doi:10.1038/nphys1758

[8] Wu, J.-L., Guan, D. and Quian, B. (1986) The character-

istic behaviour of the stretch-orientation zone during

high-speed PET spinning. International Polymer Proces-

sing, 1, 25-31.

[9] Gennes, P.G. (2002) A simple picture for structural

glasses. Comptes Rendus Physique, 3, 1263-1268.

doi:10.1016/S1631-0705(02)01387-7

[10] Wu, J.-L. (2009) Unified model theory of the glass tran-

sition: (Part 1) intrinsic 8 orders of 2D mosaic geometric

structure. Journal of Materials Science and Engineering,

3, 69-83.

[11] Lubchenko, V. and Wolynes, P.G. (2003) Origin of the

boson peak and thermal conductivity plateau in low

temperature glasses. Proceedings of the National Acad-

emy of Sciences, 100, 1515-1518.

doi:10.1073/pnas.252786999

[12] Greaves, G.N., Meneau, F., Majérus, O., Jones, D.G. and

Taylor, J. (2005) Identifying vibrations that destabilize

crystals and characterize the glassy state. Science, 308,

1299-1302. doi:10.1126/science.1109411

[13] Zallen, R. (1983) The physics of amorphous solids. Wi-

ley, New York.

[14] Wu, J.-L. (2009) Unified model theory of the glass tran-

sition: (Part 2) fixed point of self-similar Lennard-Jones

potentials in the glass transition. Journal of Materials

Science and Engineering, 3, 58-64.

[15] Wu, J.-L. (2009) Unified model theory of the glass tran-

sition: (Part 3) fixed point of second virial coefficients in

the glass transition. Journal of Materials Science and

Engineering, 3, 31-39.

[16] Laird, B.B. and Bembenek, S.D. (1996) Localization and

the Glass Transition, Journal of Physics: Condensed Ma-

tter, 8, Article ID: 9569.

doi:10.1088/0953-8984/8/47/064

[17] Barkai, E., Naumov, E.A., Vainer, Yu.G., Bauer, M. and

Kador, L.L. (2003) Statistics for random single-mo-

lecule line shapes in a glass. Physical Review Letters, 91,

1-4. doi:10.1103/PhysRevLett.91.075502

[18] Wu, J.-L. (2009) Unified model theory of the glass tran-

sition: (Part 4) Theoretical proof of the standard WLF

equation in the glass transition. Journal of Materials Sci-

ence and Engineering, 3, 76-82.

[19] Mechler, S., Macht, M.-P., Schumacher, G., Zizak, I. and

Wanderka, N. (2010) Frustration of the stable Zr-Ti-Ni

quasicrystal as the basis of glass formation. Physical Re-

view B, 81, 1-4. doi:10.1103/PhysRevB.81.180101

[20] Coslovich, D. and Pastore, G. (2007) Understanding fra-

gility in supercooled Lennard-Jones mixtures: I. Locally

preferred structures. Journal of Chemical Physics, 127,

1-13. doi:10.1063/1.2773716

[21] Shin, H.K. (2010) Vibrational relaxation of NO-(v = 1) in

icosahedral (Ar) 12NO-clusters. Journal of Chemical

Physics, 132, Article ID: 104302. doi:10.1063/1.3339385

[22] Tanaka, H. (2003) Roles of local icosahedral chemical

ordering in glass and quasicrystal formation in metallic

glass formers. Journal Physics: Condensed Matter, 15,

491-498. doi:10.1088/0953-8984/15/31/102

[23] Jain, T.S. and de Pablo, J.J. (2005) Local structure and

motions in a supercooled polymer. Journal of Chemical

Physics, 122, Article ID: 174515. doi:10.1063/1.1888505

[24] Lubchenko, V. and Wolynes, P.G. (2003) Barrier soften-

ing near the onset of nonactivated transport in super-

cooled liquids: Implications for establishing detailed con-

nection between thermodynamic and kinetic anomalies in

supercooled liquids. Journal of Chemical Physics, 119,

Article ID: 9088. doi:10.1063/1.1614180

[25] Reichl, L.E. (1980) A modern course in statistical physics.

University of Texas Press, Dallas.

[26] Pathria, R.K. (1977) Statistical mechanics. Pergamon

Press, Oxford.

[27] Williams, G. and Watts, D.C. (1970) Non-symmetrical

dielectric relaxation behavior arising from a simple em-

pirical decay function. Transactions of the Faraday Soci-

ety, 66, 80-85. doi:10.1039/tf9706600080

[28] Physics Survey Committal (1986) Physics through the

1990s, condensed-matter physics. National Academy,

Washington.

[29] Frisch, U. (1995) Turbulence. Cambridge University,

Cambridge.

[30] de Gennes, P.G. (1985) Scaling concepts in polymer

physics. Cornell University, New York.

[31] Lubchenko, V. and Wolynes, P.G. (2001) Intrinsic quan-

tum excitations of low temperature glasses. Physical Re-

view Letters, 87, 1-4.

doi:10.1103/PhysRevLett.87.195901

[32] Kent, J.A. (2007) Riegel’s handbook of industrial chem-

J.-L. Wu / Natural Science 3 (2011) 580-593

593

istry and biotechnology. Vol. 1, 11th Edition, Springer,

New York.

[33] Frank, H.P. (1986) Polypropylene. Gordon and Breach

Science, New York.

[34] Zhao, D., Fan, Q., Quian, R. and Xiu, D. (1981) Rela-

tionship between the zero shear rate viscosities of PP

melt and its viscosity average molecular weights. Bulle-

tin of Macromolecula, 5, 385-388.

[35] Wright, W.B., Budakian, R., Pine, D.J. and Putterman,

S.J. (1997) Imaging of intermittency in ripple-wave tur-

bulence. Science, 278, 1609-1216.

doi:10.1126/science.278.5343.1609

[36] Vassilicos, J.C. (2001) Intermittency in turbulence flows.

Cambridge University, Cambridge, 44-63.