Journal of Applied Mathematics and Physics
Vol.04 No.01(2016), Article ID:62632,6 pages
10.4236/jamp.2016.41006
An Economic Model of Bystanders’ Behaviour
Yuriko Isada1, Nobuko Igaki1, Aiko Shibata2
1School of Policy Studies, Kwansei Gakuin University, Hyogo, Japan
2Board of Trustee, International Christian University, Tokyo, Japan



Received 2 December 2015; accepted 5 January 2016; published 12 January 2016
ABSTRACT
In this paper, we deal with a classroom where bullying is occurring and assume that if a number of bystanders who tattle bullying exceeds a threshold, then bullying is stopped. Bystanders’ behaviour is formulated as a non-cooperative game, with negative externality, retaliation cost and reporting cost. Our research shows that to stop bullying, it is useful to raise the cost of negative externality and to reduce the retaliation cost and or the reporting cost. Additionally, it is shown that small class is effective in preventing bullying.
Keywords:
Bullying, Non-Corporative Game, Small Class, Free Rider

1. Introduction
Bullying is one of many serious problems in the field of education. The number of recognized incidents of bullying in 2013 was 185,860 according to the results of survey by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) in Japan [1]. In 2013, compared to 2012, the total number of recognized incidents of bullying remained almost unchanged, however, bullying incidents increased at elementary schools. Furthermore, there were 240 student suicides in 2013 compared to 196 students in 2012, 3.8% of those had been caused by bullying compared 3.1% in 2012. These facts suggest that the damage caused by bullying had been aggravated and bullying was recognized as crime recently. Magata [2] indicated that most incidents of bullying are criminal acts and illustrated the types of bullying that are criminal activities. Morita [3] emphasised the importance of by standers’ behaviour.
In this paper, we consider both the retaliation cost and the reporting cost and focus on the bystander’s behaviour. he retaliation cost was dealt in Shibata et al. [4] and the reporting cost was dealt in Isada et al. [5]. Actually, our model in this paper is a generalised model of both models [4] [5].
This paper comprises several sections in which different aspects of the bystander’s behaviour around bullying are discussed. Section 2 describes our model in detail. The Nash equilibrium within the model is analysed in section 3. Section 4 discusses numerical experiments with changes to class size and the impact of these changes on bystander’s behaviour. Our conclusions are presented in Section 5.
2. An Economic Model of by Standers’ Behaviour in Bullying
There are three kinds of students in this situation; the bully, the bullied child and by standers. In this paper we only focus on bystanders’ behaviour in a classroom where there is bullying. Suppose that that is n by standers in the class each bystander can take behaviour R, where a student reports bullying to a teacher, or behaviour S, where a student does not report the bullying. Bullying is resolved when more than t students report the bullying.All students are initially granted a utility level w. When bullying occurs, students incur a negative externality (disutility) b. The retaliation cost c is incurred for students who select behaviour R, only when the bullying could not be stopped despite reporting it. The reporting cost e is constantly incurred for student who selects behaviour R, regardless of whether bullying is stopped or not.
Then, a non-cooperative n-person game model [6] [7] is formulated shown in Table 1 . Each value shows the student’s gain in each case, where X denotes the number of reporters other than himself of herself.
3. Nash Equilibrium in the Economic Model
Each bystander play this game according to Table 1. Suppose each bystander has the same probability of reporting, q. When bystanders other than oneself select behaviour R with a probability q, the probability of case 1, 2 and 3 are  respectively as shown below:
respectively as shown below:
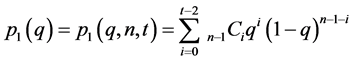 (1)
(1)
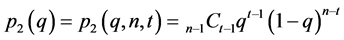 (2)
(2)
 (3)
(3)
 (4)
(4)
The Expected utility of 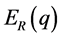 when a bystander selecting behaviour R, and the Expected utility of
when a bystander selecting behaviour R, and the Expected utility of 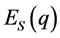 when a bystander selecting behaviour S are expressed with the following equations.
when a bystander selecting behaviour S are expressed with the following equations.
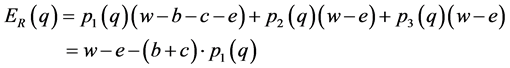 (5)
(5)
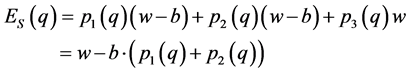 (6)
(6)
 is the state when all bystanders select behaviour R and
is the state when all bystanders select behaviour R and 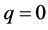 is the state when all bystanders select behaviour S. When
is the state when all bystanders select behaviour S. When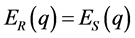 , the result is as
, the result is as . Let’s denote that
. Let’s denote that 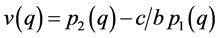 .
.
As we saw in Figure 1, from and
and , there are two values of q which hold
, there are two values of q which hold 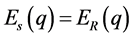 when
when 








Table 1. Changes to student’s gain by the number of reporters when selecting either behaviour R or S.
Figure 1. Two intersections of 

Let them denote

Figure 2 shows the relationship between expected utilities 



As we saw in Figure 2, 






Proposition 1
1) A pure strategy Nash equilibrium always exists in which no student reports bullying.
2) If 


3) When




Figure 3 is a graph of 



When examining Figure 1 and Figure 4, we see that we can expand the range [




Proposition 2
1) A decrease in 


2) A decrease in c causes a decrease in 

4. The Impact of Changing the Class Size
Let us examine changes in 








Figure 6 is a graph that shows the value of and 









[



Figure 2. Expected utility when there are two intersections of 

Figure 3. A graph of 
Figure 4. A graph of 
Figure 5. A graph of 

Figure 6. A graph of


5. Conclusion
In this paper we modelled the bystanders’ behaviour with bullying in a non-cooperative n-player game. The three costs are the cost of negative externality, the retaliation cost and the reporting cost, were considered in this model. If the probability of reporting q is larger than the lower limit






Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers 25350468.
Cite this paper
Yuriko Isada,Nobuko Igaki,Aiko Shibata, (2016) An Economic Model of Bystanders’ Behaviour. Journal of Applied Mathematics and Physics,04,33-38. doi: 10.4236/jamp.2016.41006
References
- 1. MEXT (2014) Results of the 2013 Survey of Problem Behaviour of Students and Various Issues with Instructing Students. http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/gijiroku/__icsFiles/afieldfile/2014/12/18/1354117_5.pdf
- 2. Magata O. (2013) Ijime to hanzai. [Bullying and Crime] Chuo. http://www.yomiuri.co.jp/adv/chuo/opinion/20140303.htm
- 3. Morita, Y. (2010) Ijime to ha nanika [What Is Bullying].Chuko Shinsho, Tokyo.
- 4. Shibata, A., Mori, T., Okamura, M. and Soyama, N. (2008) An Economic Analysis of Apathetic Behavior: Theory and Experiment. The Journal of Socio-Economics, 37, 90-107. http://dx.doi.org/10.1016/j.socec.2006.12.026
- 5. Isada, Y., Igaki, N. and Shibata, A. (2015) A Game-Theoretic Model for Bystanders’ Behaviour in Classes with Bullying. Open Journal of Social Sciences, 3, 97-102. http://dx.doi.org/10.4236/jss.2015.39015
- 6. Nash, J. (1950) Equilibrium Points in n-Person Games. Proceedings of the National Academy of Sciences of the United States of America, 36, 48-49. http://dx.doi.org/10.1073/pnas.36.1.48
- 7. Nash, J. (1951) Non-Cooperative Games. Annals of Mathematics Second Series, 54, 286-295. http://dx.doi.org/10.2307/1969529








