Received 22 November 2015; accepted 5 January 2016; published 12 January 2016

ABSTRACT

In this paper, we consider scheduling problems with general truncated job-dependent learning effect on unrelated parallel-machine. The objective functions are to minimize total machine load, total completion (waiting) time, total absolute differences in completion (waiting) times respectively. If the number of machines is fixed, these problems can be solved in 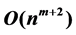time respectively, where m is the number of machines and n is the number of jobs.

Keywords:

Scheduling, Unrelated Parallel Machines, Truncated Job-Dependent Learning

1. Introduction

In modern planning and scheduling problems, there are many real situations where the processing time of jobs may be subject to change due to learning effect. An extensive survey of different scheduling models and problems with learning effects could be found in Biskup [1]. More recently, Janiak et al. [2] studied a single processor problem with a S-shaped learning model. They proved that the makespan minimization problem is strongly NP-hard. Lee [3] considered scheduling jobs with general position-based learning curves. For some single machine and a two-machine flowshop scheduling problems, they presented the optimal solution respectively. Lee [4] considered single-machine scheduling jobs with general learning effect and past-sequence-dependent setup time. For some single machine scheduling problems, they presented the optimal solution respectively. Lee and Wu [5], and Wu and Lee [6] considered scheduling jobs with learning effects. They proved that some single machine and flowshop scheduling problems can be solved in polynomial time respectively. Lee et al. [7] considered a single-machine scheduling problem with release times and learning effect. Lee et al. [8] considered a makespan minimization uniform parallel-machine scheduling problem with position-based learning curves. Lee and Chung [9], Sun et al. [10] [11], and Wang et al. [12] considered flow shop scheduling with learning effects. Wu et al. [13], Wu et al. [14], Wu et al. [15] and Wang et al. [16] considered scheduling problems with the truncated learning effect.

Recently, Wang et al. [17] considered several scheduling problems on a single machine with truncated job-dependent learning effect, i.e., the actual processing time of job 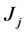is 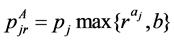if it is sche-

duled in the rth position of a sequence, where is the job-dependent learning index of job, and b is a truncation parameter with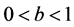. In this paper, we study scheduling problems with general truncated job- dependent learning effect on unrelated parallel-machine. The objective is to minimize total machine load, total completion (waiting) time, total absolute differences in completion (waiting) times respectively.

2. Problems Description

There are n independent jobs 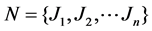to be processed on m unrelated paralle-machine 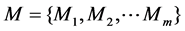. Let 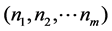denote a job-allocation vector, where 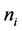denotes the number of jobs assigned to machine, and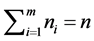. In this paper, we assume that the actual processing time of job 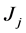scheduled on machine 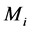is

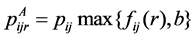, (1)

where 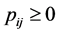denotes the normal (basic) processing time of job on machine, is the position of a sequence, is a truncation parameter with, is the general case of positional learning for job on machine, special is the polynomial learning index for job on machine, is the exponential learning index for job on machine.

Let and be the completion and waiting time for job on machine respectively. The goal is to determine the jobs assigned to corresponding each machine and the corresponding optimal sche-

dule so that the following objective functions is to be minimized: the total machine load, the total completion (waiting) times, the total absolute differences in completion (waiting) times，where denotes the makespan of machine. Using the three-field notation [18] the problems can be denoted as, where denote the model (1),.

3. Main Results

Let denote the actual processing time of a job when it is scheduled in position on machine, then, , , are defined similarly.

Lemma 1. For a given permutation on machine,

(Kanet [19])

(Bagchi [20]).

If the vector is given, let be a variable such that if job is assigned at position on machine, and, otherwise. Then, the problem (where) can be solved by the following assignment problem:

(2)

(3)

(4)

or 1, (5)

where for, for, for, for, for.

Now, the question is how many vectors exist. Obviously may be 0, 1, 2, , n. So if the numbers of jobs assigned to the first machines is given, the number of jobs assigned to the last machine is then determined uniquely (). Therefore, the upper bound of is. Based on the above analysis, we have the following result.

Theorem 1. For a given constant, can be solved in time, where

.

Proof. As discussed above, to solve the problem, polynomial number (i.e.,) of assignment problems need to be solved. Each assignment problem is solved in time (by using the Hungarian method). Hence, the time complexity of the problem can be solved in time, where

.

Note that if the number of machines is fixed, then the problem can be solved in polynomial time. Based on the above analysis, we can determine the optimal solution for the problem via the following algorithm:

Algorithm 1

Step 1. For each possible vector, solve the assignment problem (2)-(5). Then, obtain the optimal schedule and the corresponding objective function.

Step 2. The optimal solution for the problem is the one with the minimum value of the objective function, where.

The following example illustrates the working of Algorithm 1 to find the optimal solution for the problem.

Example 1. There are jobs and, The number of machines is and, , , , , , , , , , , , , , , , , , , , are given.

Solution. When, the positional weights on machine are, , , ,. Then values are given in Table 1 (the bold value is the optimal solution of the assignment problem (2)-(5)).We solve the assignment problem (2)-(5) to

When, the positional weights on machine and are, , , ,. Then values are given in Table 2. We solve the assignment problem

(2)-(5) to obtain that the optimal schedule on machine is, and on machine is. The objective function is

When, the positional weights on machine and are, , , ,. Then values are given in Table 3. We solve the assignment problem (2)-(5) to obtain that the optimal schedule on machine is, and on machine is. The objective function is

When, the positional weights on machine and are, , , ,. Then values are given in Table 4. We solve the assignment problem (2)-(5) to obtain that the optimal schedule on machine is, and on machine is. The objective function is

When, the positional weights on machine and are, , , ,. Then values are given in Table 5. We solve the assignment problem (2)-(5) to obtain that the optimal schedule on machine is, and on machine is. The objective function is

When, the positional weights on machine and are, , , ,. Then values are given in Table 6. We solve the assignment problem (2)-(5) to obtain that the optimal schedule on machine is. The objective function is

Hence, the optimal schedule on machine is, and on machine is. The optimal objective function is

Acknowledgements

Hsu was supported by the Ministry Science and Technology of Taiwan under Grant MOST 104-2221-E-252- 002-MY2.

Cite this paper

Jibo Wang,Chou-Jung Hsu, (2016) Unrelated Parallel-Machine Scheduling Problems with General Truncated Job-Dependent Learning Effect. Journal of Applied Mathematics and Physics,04,21-27. doi: 10.4236/jamp.2016.41004

References

NOTES

^*Corresponding author.