Received 22 November 2015; accepted 5 January 2016; published 12 January 2016

ABSTRACT

Solving large scale system of Simultaneous Linear Equations (SLE) has been (and continue to be) a major challenging problem for many real-world engineering and science applications. Solving SLE with singular coefficient matrices arises from various engineering and sciences applications [1]-[6]. In this paper, efficient numerical procedures for finding the generalized (or pseudo) inverse of a general (square/rectangle, symmetrical/unsymmetrical, non-singular/singular) matrix and solving systems of Simultaneous Linear Equations (SLE) are formulated and explained. The developed procedures and its associated computer software (under MATLAB [7] computer environment) have been based on “special Cholesky factorization schemes” (for a singular matrix). Test matrices from different fields of applications have been chosen, tested and compared with other existing algorithms. The results of the numerical tests have indicated that the developed procedures are far more efficient than the existing algorithms.

Keywords:

Generalized Inverse Algorithms, Simultaneous Linear Systems, Matrix Inverse, Singular Matrix, Pseudo Inverse, Cholesky Factorization

1. Introduction

In scientific computing, most computational time is spent on solving system of Simultaneous Linear Equations (SLE) which can be represented in matrix notations as

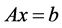(1.1)

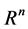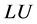where is a singular/non-singular matrix, and b is a given vector in. For practical engineering/ science applications, matrix A can be either sparse (for most cases), or dense (for some cases). For a non-sin- gular coefficient matrix A, direct methods (Cholesky factorization, algorithm, decomposition, etc) or iterative methods (Conjugate Gradient algorithm, Bi-Conjugate Stabilization, GMRES, etc.) are used to solve Equation (1.1). If the coefficient matrix is singular or rectangular, the above mentioned direct and iterative methods cannot be used to solve Equation (1.1) and thus generalized inverse is needed to solve the unknown solution vector x in Equation (1.1).

The generalized (or pseudo) inverse of a matrix is an extension of the ordinary/regular square (non-singular) matrix inverse, which can be applied to any matrix (such as singular, rectangular etc.). The generalized inverse has numerous important engineering and sciences applications. Over the past decades, generalized inverses of matrices and its applications have been investigated by many researchers [1]-[6]. Generalized inverse is also known as “Moore-Penrose inverse” or “g-inverse” or “pseudo-inverse” etc.

In this paper we introduce an efficient (in terms of computational time and computer memory requirement) generalized inverse formulation to solve SLE with full or deficient rank of the coefficient matrix. The coefficient matrix can be singular/non-singular, symmetric/unsymmetric, or square/rectangular. Due to popular MATLAB software, which is widely accepted by researchers and educators worldwide, the developed code from this work is written in MATLAB language.

The rest of this paper is organized as follows. In Section 2, we discuss background of generalized inverse. In Section 3, we give a description of the algorithm. This section also describes the efficient generalized inverse formulation (which uses modified Cholesky factorization). In Section 4, we present comparison of numerical performances of the proposed algorithm with other existing algorithms. Extensive set of coefficient matrices (including rectangular, square, symmetrical, non-symmetrical, singular, non-singular matrices) obtained from well-established/popular websites [8] [9] were tested and the numerical performance in terms of timings, error norm were compared with other algorithms. Finally, conclusions are drawn in Section 5.

2. Singular Value Decomposition (SVD) and the Generalized Inverse

A general (square or rectangular) matrix 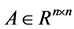can be decomposed as

(2.1)

where

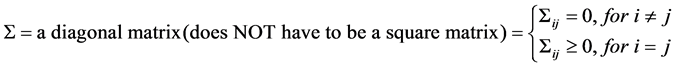(2.2)

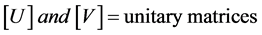
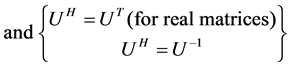(2.3)

Let A be a singular matrix of size 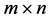and let k be the rank of the matrix. Based on Equation (2.1), one has

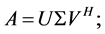
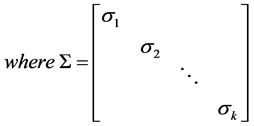
with

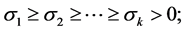(2.4)

and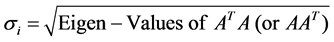

Note: Eigen-values of 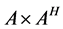and Eigen-values of 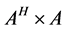are the same. However, the Eigen-vectors of and Eigen-vectors of are “NOT” the same.

Then, the generalized inverse of is the matrix and is given as

(2.5)

where

and is the diagonal matrix, with.

3. Efficient Generalized Inverse Algorithms [1]-[3] [5] [6]

Moore-Penrose inverse can be computed using Singular Value Decomposition (SVD), Least Squares Method, QR factorizations, Finite Recursive Algorithm [2] [3], etc. In this work, our numerical algorithms have been based on:

(a) The “special Cholesky factorization” (for symmetrical/singular coefficient matrix), and

(b) The generalized inverse of a product of 2 matrices [6] and can be described in the following paragraphs.

The Moore-Penrose inverse (or generalized inverse or pseudo inverse) of a matrix (not necessarily a square matrix) is the unique matrix which satisfies the following four conditions:

1. General condition:

2. Reflexive condition:

3. Normalized condition:

4. Reverse normalized condition:

Consider with a square coefficient matrix, and let the rank be less than the size of the matrix (if r is the rank of the matrix, then). Let the size of the known right-hand-side vector be. Consider a symmetric positive matrix with rank (here, the matrix plays the same role as matrix in Equation (1.1)), then based on the theorem presented in [6], there exists a unique such that:

(3.1)

In Equation (3.1), matrices have the dimensions, respectively.

M is the upper triangular (special) Cholesky factorized matrix and contains exactly zero rows. Removing the zero rows from M, one obtains a (upper, rectangular) matrix.

(3.2)

In this work, the upper triangular (special) Cholesky factorized matrix can be obtained by the regular/ standard Cholesky factorization, with the following modifications:

a) When the diagonal term of the current row is very close to zero, then factorization of this dependent row is skipped.

b) When the current row is factorized, all previous rows were used except those dependent row(s).

Consider the generalized inverse of a matrix product [1] [6]

(3.3)

From Equation (3.3), if then

(3.4)

If and A is a matrix of rank r, then one obtains from Equation (3.3)

(3.5)

Let us consider regular inverse in Equation (3.5) in place of generalized inverse

(3.6)

Using Equation (3.4),

(3.7)

From Equations (3.1)-(3.2) and Equation (3.6) one obtains,

(3.8)

Thus, Equation (3.7) becomes

(3.9)

While MATLAB solution can be obtained by implying the generalized inverse [see Equation (3.9)] to be formed explicitly, our main idea is to solve SLE where is a known right-hand-side vector.

4. Numerical Performance of ODU Generalized Inverse Solver

Based on the detailed algorithms explained in Section 3, the numerical performance of our proposed procedures are evaluated in this section. The known RHS vector can be random vector, or can be chosen such a way that the unknown solution vector.

We also compared the performance of our algorithm with the efficient algorithm described in [6] and also with MATLAB built-in function [7] for computing the generalized inverse explicitly. We use MATLAB version 7.6.0.324 (R2008a) on Intel Core 2 CPU, 2.13 GHZ, 2GB RAM, Windows XP Professional SP3 for numerical comparisons.

Table 1 and Table 2 records the times (in seconds) taken by our proposed algorithm, the algorithm mentioned in [6] and MATLAB built-in function [7]. For our convenience, we represent our algorithm with, algorithm in [6] with and MATLAB built-in function with. In addition, we have also presented the error norm for all the test matrices.

5. Conclusion

In this paper, various efficient algorithms for solving SLE with full rank, or rank deficient have been reviewed, proposed and tested. The developed numerical procedures can be applied to solve “general” SLE (in the form, where the coefficient matrix could be square/rectangular, symmetrical/unsymmetrical, non-singular/singular). The users have option to choose either a direct solver or an iterative solver inside the generalized inverse to solve for SLE. Numerical results have shown that the proposed algorithms are highly efficient as compared to existing algorithms [6] (including the popular MATLAB built-in function) [7].

Acknowledgements

The authors would like to acknowledge Gelareh Bakhtyar for her useful discussions.

Cite this paper

S. Kadiam Bose,D. T. Nguyen, (2016) Efficient Generalized Inverse for Solving Simultaneous Linear Equations. Journal of Applied Mathematics and Physics,04,16-20. doi: 10.4236/jamp.2016.41003

References