Journal of Materials Science and Chemical Engineering
Vol.04 No.01(2016), Article ID:62592,7 pages
10.4236/msce.2016.41001
Flocculation Efficiency in Taylor-Couette Flow
Qing Chang, Yuhong Mao, Liyun Zeng, Changquan Yu
School of Environmental and Municipal Engineering, Lanzhou Jiaotong University, Lanzhou 730070, Gansu, China



Received 15 July 2015; accepted 5 January 2016; published 11 January 2016
ABSTRACT
Velocity field data were acquired for Taylor-Couette flow in the annulus gap between a rotating inner cylinder and a fixed concentric outer cylinder by particle image velocimetry. The flocculation efficiencies were also obtained in the same Taylor-Couette flow under the conditions corresponding to the velocity field measurement. It was shown that the flocculation efficiencies reach the maximum values due to the closed vortices in WVF and their contraction and expansion with time, but out of WVF range, the comparatively low flocculation efficiencies were obtained due to the no-closed vortices connected with each other.
Keywords:
Flocculation, PIV, Taylor-Couette Flow, Turbulent Flow, Water Treatment

1. Introduction
Flocculation is a primary water treatment process that changes the size distribution of particles from a large number of small particles to a small number of large particles for removal in later processes. Particles increase in size because of collision with and attachment to other particles. These collisions can occur through the random Brownian motion of particles, fluid motion, and differential settling rate of particles. As far as the fluid motion is concerned, the work of Smoluchowski is the cornerstone of flocculation. According to Smoluchowski theory [1] [2], the velocity gradient leads to collisions of particles, therefore, induces flocculation. He proposed the equation for laminar flocculation as follows.
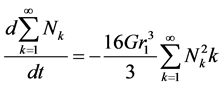 (1)
(1)
in which k is subscript denoting particle size, N is number concentration of the particles, t is time, r1 is the radius of primary particle, and G is the velocity gradient. In order to use Smoluchowski equation in turbulent flocculation condition, Camp and Stein developed the G-value as follows [1] [2].
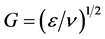 (2)
(2)
in which ε is the power input per unit mass, and ν is the kinematic viscosity. From that time, it has been widely accepted that the mixing conditions with the same G-value are almost identical from the flocculation point of view, and the G-value has been widely used in the design and scale-up of mixing process components. But since the middle of 1980s, some research results have been published that criticize and question the use of the G-value as a valid basis for the design of flocculation basins. For example, Oldsue [3] stated that different performances are expected from different impellers at the same G-value. Cleasby [4] said that the G-value is only valid for vortices whose sizes are smaller than those necessary for flocculation in both water and wastewater treatment. Han and Lawler [5] stated that the importance of the velocity gradient has been apparently overemphasized in traditional view of flocculation. In addition, it was proved [6] that the grid flocculation developed in recent years shows the excellent performances, but the G-value equals zero in some distances from the grids. In the last several decades, many researchers attempt to discuss flocculation dynamics in turbulent condition directly from turbulent flow theory. According to Kolmogorov’s local isotropic theory [7], the energy input into the fluid is primarily used for the formation of large vortices during flocculation. These large vortices accomplish most of the momentum transport but only a small amount of energy dissipation. Energy transfer in turbulent flows results in the formation of turbulent vortices of decreasing size until the energy is dissipated by viscous forces. Those vortices which have the same size approximately as the particles are thought to be responsible for flocculation. But this microscale vortices theory is only applicable to small vortices, not vortices of other size. In summary, the reasons which induce the turbulent flocculation are still not very clear up to now.
It is well known that Taylor-Couette device is one of the traditional flocculation reactors [2]. The Taylor- Couette device [8]-[10] consists of two concentric cylinders. In this device the wall-driven fluid flow in the annulus between a rotating inner cylinder and a fixed concentric outer cylinder has been studied extensively for nearly a century. This canonical flow system exhibits instabilities as the angular velocity of the inner cylinder is increased from rest. The flow undergoes a series of transitions that give rise to many flow states including laminar Taylor vortex flow (TVF), wavy vortex flow (WVF), modulated wavy vortex flow (MWVF), and turbulent Taylor vortex flow (TTVF). This TTVF becomes increasingly complex as angular velocity of the inner cylinder is continuously increased until the vortex structures themselves eventually become indiscernible. These flow transitions occur at specific values of the azimuthal Reynolds numbers, Re, defined as:
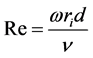 (3)
(3)
where ω is the inner cylinder angular velocity, ri is the radius of the inner cylinder, d = r0 − ri is the annular gap width, and ν is the kinematic viscosity. The critical azimuthal Reynolds number at which Taylor instability occurs, Rec, depends upon the specific geometry of the flow device used(L. Wang et al. 2005; M. Soos et al. 2007). But it is convenient to define a reduced-Reynolds number ratio R(=Re/Rec) to parameterize the flow. L. Wang et al. found that the flow is approximately in the laminar vortex flow(TVF) regime when 1 < R ≤ 5.0, and in the wavy vortex flow(WVF) regime when 5.0 < R ≤ 20, and in the modulated wavy vortex flow(MWVF) regime when 20 < R ≤ 40, and in the turbulent vortex flow(TTVF) regime when R > 40 for their apparatus according to observation of the sequences of instantaneous velocity fields [6] [8]-[12].
On the other hand, it is known that the particle image velocimetry (PIV) technique can measure the velocity of an entire flow field instantaneously to quantitatively reveal global structures of a complicated and unsteady flow [13]. It has been mainly applied in the fields of fluid dynamics and only a few applications are reported in the fields of water treatment. Recent technological advancement in optics and computer technology, which have resolved the problems of storage space and camera frequency, has enhanced the potential, therefore, now it is possible to analyze the velocity fields of Taylor-Couette flow.
By using the advanced technology of PIV and Taylor-Couette device, this study attempts to relate the flocculation efficiency to turbulent flow field, thus reveal some reasons which induce the turbulent flocculation and to give the better understanding of turbulent flocculation. It will be very helpful to researchers, designers and operators of flocculation in water treatment. To our knowledge, the relationships between the PIV data and flocculation efficiency presented here are the first reported.
2. Experiment
2.1. Equipment
The Taylor-Couette flow apparatus used in the present research was made in our laboratory. It consists of two concentric cylinders. The rotating inner cylinder is made of stainless steel, and has diameter 2ri = 75 mm. The fixed outer cylinder is made of Plexiglas, and has diameter 2ro = 100 mm. The resulting gap width is d = ro − ri = 12.5 mm, the radius ration is η = ro/ri = 0.75. The cylinder height L = 440 mm, the cylinder aspect ratio, Г = L/(r0 − ri) = 35.2. The inner cylinder is fitted with stainless steel drive shafts on the central axis. A ABB motor is used to drive the inner cylinder.
The FlowMap PIV system used in this study was bought from Dantec Dynamics of Danish. It consists of doubled pulsed Nd:YAG laser, high speed Flowsense
2.2. Method
2.2.1. Flow field Measurement
Optical distortions were eliminated by enclosing the outer cylinder in a square Plexiglas box and using a working fluid having a refractive index matched to that of Plexiglas. The flow was seeded with small tracer particles that reflect and scatter the laser light, and the CCD camera perpendicular to the laser sheet was used to capture the particle images in a plane illuminated by a laser light sheet. The FlowManager software was used to both Control the image acquisition, keep track of the recorded data, the set-ups and the experimental configuration. Data analysis is available in the FlowManager Analysis option. Besides functioning as a database, The FlowManager software also control the FlowMap system HUB through the run online menus. The maximum data collection rate for the system is 15 velocity vector fields per second. For each of reduced-Reynolds number ratio R studied, about 500 image pairs were captured. The time between laser pulses for an image pair vary with velocity fluid, Polyamide particles with an average diameter of 20 μm were used as seed particles at a concentration of 21.43 mg/L (10 particles within each interrogation area). The particles have a density of 1.03 × 103 kg/m3. The kinematic viscosity of the fluid was measured as 1.006 × 10−6 m2/s. To ensure that the flow state in the device was identical for each value of R studied, all experiments were performed using the following protocol. The rotation rate of the inner cylinder was maintained at any given angular velocity for at least 10 min, until the desired value of R was reached, and then the flow was expected to equilibrate for approximately 10 min before PIV data were collected.
2.2.2. Flocculation Test
2% suspension of kaolin was prepared as stock solutions. 1500 ml of tap water and 7.5 ml of above kaolin suspension were added to Taylor-Couette reactor. After the strong mixing by rotating of inner cylinder (500 rpm),
Figure 1. Schematic diagram of measuring system for Taylor-Couette flow field.
the turbidity of this water sample equals 100 NTU. 1%PAC solutions were added in different dosages respectively to water samples in the reactor which were stirred by the rotating of inner cylinder at 500 rpm of uniform speed for 2 min, followed by the slow stirring at different rotating speed for 10 min. Later, 10 minutes of settling time was required. After these procedures, the supernatants were drawn from the place of
3. Result
3.1. Velocity Vector map of Meridional Plane
Annulus gap meridianal plane of Taylor-Couette reactor is shown in Figure 2.
The mean velocity vector map of the meridianal plane in different rotation rates were obtained by PIV, as shown in Figure 3, n is the rotating rate of inner cylinder (r/min), R is the reduced Reynolds number ratio (=Re/Rec) which n corresponds to. For this apparatus, the critical Reynolds number Rec = 83, when laminar Taylor vortices appear. It is nearly the same as that reported by L. Wang et al. (L. Wang et al. 2005; M. Soos et al. 2007). Figure 3 shows there is a regular distribution of vortices in the axial direction, and the spinning direction of neighboring vortices is opposite. The existence of vortex at R = 1.7 shows this canonical flow system start to exhibit instabilities when n is very low. It can be observed that the numbers of vortices in the annulus gap first increase and then decrease with the increase in rotation speed of inner cylinder. It can be also observed that with the increase in rotation speed of inner cylinder, the vortex state gradually changes from the left to the right. There are fewer initial vortices which are open and connect with each other when R = 1.7 - 5.8. This indicates that vortices were just beginning to form in this range. Out of the range, many individual, integrated and separated vortices form when R is greater than 5.8, but the integrity of vortices gradually decrease with the continual increase in rotation speed of inner cylinder, and neighboring vortices connect with each other again, producing non-closed or open vortices at last.
Figure 2. Schematic diagram of measurement area on meridianal plane.
Figure 3. Mean velocity vector map of meridional plane.
The instantaneous velocity vector maps of the meridianal plane were measured in different time and at constant rotation speed by PIV. From large amount of instantaneous velocity vector map, a regular change can be observed as long as the same rotation rate of the inner cylinder remains unchanged. The similar vortices periodically occur, and the wavelength is regular. Therefore, a periodical change of vortex state can be observed in these instantaneous velocity vector maps within a certain range. But, the differences between instantaneous velocities fields in one cycle decrease, and the periodicity of vortex state reappearance become shorter and shorter with the increase in rotation speed of the inner cylinder. At last, this periodical reappearance of vortex state disappear when R is greater than 40. A time sequence of eight instantaneous velocity field for R = 11.6 are shown in Figure 4. The numbers in the bottom of figure denote the time sequence of instantaneous velocity vector field. It can be observed that the instantaneous vortices states vary with time. The vortex volume periodically expands and contracts. And the locations of the vortex centers oscillate both axially and radially.
3.2. Effect of Flow Field on Flocculation Efficiency
The flocculation efficiencies of different PAC dosages for different rotating rate of inner cylinder were obtained as shown in Figure 5.
From Figure 5, it can be seen that all of the turbidity removal rate (%) of different PAC dosages first increase, and then decrease with the increase in the rotating rate. The flocculation efficiencies reach the maximum nearly in the same range between the 10 rpm and 30 rpm. It can be visually observed that the flocs produced in this range are large and settle fast, but the flocs produced out of this range, before or after, are comparatively tinny, settle slowly, and difficult to separate from water.
4. Discussion
By using Equation (3), we calculated the azimuthal Reynolds numbers, Re, and the reduced-Reynolds number ratio R (=Re/Rec) for every rotating rate studied in this research, as shown in Table 1.
It can be seen that the flow regimes [9]-[11] which the R correspond are also placed in Table 1. As discussed above, the flocculation efficiencies reach the maximum values in the range between the 10 m and 30 rpm which corresponds the range of R = 5.8 to R = 20 (which falls within the WVF regime). From Figure 3, we can see all of vortices in WVF regime are closed vortices. This may be favorable for particles inside the vortex to collide each other. Liguang Wang reported that [9] [10] in the WVF regime, the bulk fluid motion was observed, and the vortices expand and contract periodically with time due to the superimposed waves on the toroidal vortices.
Figure 4. A sequence of eight instantaneous velocity vector fields for R = 11.6.
Figure 5. Flocculation efficiency in different rotating rate.
Table 1. Relationship flow field and rotating rate.
The same result as Liguang Wang’s are also obtained in our research, as shown in Figure 4. Therefore it can be deduced that the vortex expansion and contraction would accelerate or slow down the motion velocity of particles inside vortex, and even change the motion direction of the particles, thus increase the possibility of collision of particles, leading the higher flocculation efficiency. But with the increase in rotation speed of inner cylinder, the flow regime changes from WVF to TTVF. In the beginning of TTVF regime, the periodical contraction and expansion of vortex have almost disappeared. The integrity of vortices gradually decrease, neighboring vortices connect with each other, producing non-closed or open vortices at last, as a result, the particles can move with water flow from one vortex to the neighboring vortex, thus decrease the possibility of collision of particles, leading the lower flocculation efficiencies. As far as R lower than that of WVF is concerned, the initial vortices are just beginning to form in this range, they are also non-closed or open, the same reason as above leading the lower flocculation efficiency.
5. Conclusions
The flocculation efficiencies reach the maximum values in the range between the 10 rpm and 30 rpm which falls within the WVF regime. But out of WVF regime, the comparatively low flocculation efficiencies are obtained;
Because the vortex in WVF is the closed vortex and periodically expands and contracts with time, WVF regime may be favorable for particles to collide each other, leading the higher flocculation efficiency.
When R is lower than that of WVF, the initial vortices are just beginning to form in this regime, which are non-closed or open vortices, leading the lower possibility of collision of particles and the lower flocculation efficiency.
With the increase in rotation speed of inner cylinder, the flow regime changes from WVF to TTVF, and the vortices change from closed vortices to no-closed vortices again which connect with each other, therefore the particles can move with water flow from one vortex to the neighboring vortex, thus decrease the possibility of collision of particles, leading the lower flocculation efficiencies.
Acknowledgements
We thank the financial support from the National Natural Science Foundation of China (No. 50878102).
Cite this paper
Qing Chang,Yuhong Mao,Liyun Zeng,Changquan Yu, (2016) Flocculation Efficiency in Taylor-Couette Flow. Journal of Materials Science and Chemical Engineering,04,1-7. doi: 10.4236/msce.2016.41001
References
- 1. Cassonl, W. and Lawler, D.F. (1990) Flocculation in Turbulent Flow: Measurement and Modeling of Particle Size Distribution. J.AWWA, 63, 54-68.
- 2. Chang, Q. (2003) The Flocculation of Water Treatment. China Chemical Industry Press, Beijing, 34-38, 167-168. (In Chinese)
- 3. Oldsue, J.Y. (1983) Fluid Mixing Technology. McGraw-Hill Book Co, New York, USA.
- 4. Cleasby, J.L. (1984) Is Velocity Gradient a Valid Turbulent Flocculation Parameter. J. Envi. Eng. ASCE, 111, 741-754.
- 5. Han, M. and Lawler, D.F. (1992) The (Relative) Insignificance of G Value in Floccu-lation. J. AWWA, 84, 79-91.
- 6. Sun, Z. and Yang, J. (1998) Study on the Treatment of Water Which Has Low Temperature and Low Turbidity by Vortices-Grid Flocculation Reactor. China Water and wastewater, 14, 32-34. (In Chi-nese)
- 7. Casson, L.W. and Lawler, D.F. (1990) Flocculation in Turbulent Flow: Measurement and Modeling of Particle Size Distributions. J. AWWA, 82, 54-68.
- 8. Kataoka, K. (1985) Encyclopedia of Fluid Mechanics. In: Taylor Vortices and Instabilities in Circular Couette Flows, Housing Gulf Publishing, Vol. 1, 237-273.
- 9. Wang, L., Olsen, M.G. and Vigil, R.D. (2005) Reappearance of Azimuthal Waves in Turbulent Taylor-Couette Flow at Large Aspect Ratio. Chemical Engineering Science, 60, 5555-5568. http://dx.doi.org/10.1016/j.ces.2005.05.024
- 10. Wang, L., Olsen, M.G. and Vigil, R.D. (2005) Reappearance of Azimuthal Waves in Turbulent Taylor-Couette Flow at Large Aspect Ratio. Chemical Engineering Science, 60, 5554-5568.
- 11. Soos, M., Wang, L., Fox, R.O., Sefcik, J. and Morbidelli, M. (2007) Population Balance Modeling of Aggregation and Breakage in Turbulent Taylor-Couette Flow. Journal of Colloid and Interface Science, 307, 433-446. http://dx.doi.org/10.1016/j.jcis.2006.12.016
- 12. Yi, M.-K. and Kim, C. (1997) Experimental Studies on the Taylor Instability of Dilute Polymer Solutions. J. Non-Newtonian Fluid Mech., 72, 113-139. http://dx.doi.org/10.1016/S0377-0257(97)00032-3
- 13. Akonur, A. (2001) Fluid Physics of a Rotating Membrane Separator. PhD Thesis, Northwestern University, Evanston, Illinois, USA.







