 Circuits and Systems, 2011, 2, 217-224 doi:10.4236/cs.2011.23031 Published Online July 2011 (http://www.SciRP.org/journal/cs) Copyright © 2011 SciRes. CS Algorithmic Optimization of BDDs and Performance Evaluation for Multi-level Logic Circ uits with Area and Power Trade-offs Saurabh Chaudhury1, Anirban Dutta2 1Department of Electrical Engineering, National Institute of Technology, Silchar, India 2Department of Electronics & Communication Engineering, National Institute of Technology, Silchar, India E-mail: saurabh1971@gmail.com Received April 27, 2011; revised May 20, 2011; accepted May 27, 2011 Abstract Binary Decision Diagrams (BDDs) can be graphically manipulated to reduce the number of nodes and hence the area. In this context, ordering of BDDs play a major role. Most of the algorithms for input variable or- dering of OBDD focus primarily on area minimization. However, suitable input variable ordering helps in minimizing the power consumption also. In this particular work, we have proposed two algorithms namely, a genetic algorithm based technique and a branch and bound algorithm to find an optimal input variable order. Of course, the node reordering is taken care of by the standard BDD package buddy-2.4. Moreover, we have evaluated the performances of the proposed algorithms by running an exhaustive search program. Experi- mental results show a substantial saving in area and power. We have also compared our techniques with other state-of-art techniques of variable ordering for OBDDs and found to give superior results. Keywords: Algorithmic Optimization, BDDs, Genetic Algorithm, Branch & Bound, Variable Ordering, Area-Power Trade-offs 1. Introduction Binary decision diagram (BDD) is an important data structure which finds wide applications specially, in the area of Boolean logic manipulation, logic synthesis, for- mal verification and testing. A Boolean function that describes a digital circuit can be represented as a BDD which is a directed acyclic graph with respect to an order and satisfying a set of properties. The number of its non- terminal nodes gives their size. For multiplexer based design styles such as Pass Transistor Logic (PTL), a smaller number of nodes directly transfers to a smaller chip area. A BDD can be implemented either in canoni- cal form, reduced order (ROBDD) or in any other spe- cific order (OBDD). If all identical nodes are shared and all redundant nodes are eliminated, the OBDD is said to be reduced (an ROBDD). The size of a BDD is strongly dependent on the order of input variables. In the current problem of variable ordering, a number of algorithms exist in this context. These variable order- ing algorithms can be broadly classified as static vari- able ordering, dynamic variable ordering and evolution- ary algorithms. Most of the variable ordering algorithms from circuit topology are based on a depth first traversal through a circuit from the primary outputs to the primary inputs [1,2]. Such an ordering works well if the circuit is tree-structured. Yet another approach to variable order- ing is gradual improvement based on variable exchange [3,4]. Though this approach is effective, the results de- pend on the initial variable orders and hence on circuit topology. R. Rudell [5] describes a dynamic variable ordering technique for an OBDD and propose two algo- rithms. The technique allows maintaining all advantages provided by the ordered BDD data structure, such as, canonicity and efficient recursive algorithms. A new variable ordering algorithms for multiple output circuits has been presented in [6] use variable interleaving, while conventional algorithms use variable appending. Chris- toph Meinel and Fabio Somenzi [7] propose another al- gorithm called linear shifting, which in many cases it leads to substantially more compact diagrams when compared to simple variable reordering. Another heuris-  S. CHAUDHURY ET AL. 218 1 tic technique for deciding which BDD variables to reor- der is simulated annealing (SA) [8]. But this technique is very slow, especially if the cost function is expensive to compute. A first attempt to use evolutionary algorithms for the variable ordering problem for BDDs is presented in [9] where the main genetic operations are partially- mapped crossover and mutation which yield better re- sults (smaller BDDs) than other dynamic reordering techniques, but they are comparably slow. Many such evolutionary algorithms are presented in [10-12]. In [13], a low power optimization technique for BDD mapped circuits using temporal correlation has been presented. Output phase assignment technique for area and power minimization has been proposed in [14], which optimizes the BDD by finding suitable output polarity of a multi- output circuit using genetic algorithm. A new and pow- erful class of optimization techniques based on scatter search [15] has been proposed, which is very aggressive and attempts to find high quality solutions at a fast rate. Scatter search optimization techniques offers a reason- able compromise between quality (BDD size) and time. In [16] we see a technique to minimize the BDD com- plexity and the time of evaluation of the function based on minimum path length which is decided by initial variable order. A detailed survey of static variable or- dering heuristics (such as topological, influential, priority ordering and variable weighing etc.) has been presented in [17] in order to minimize the overall size of resulting decision diagram. Prasad, Assi, Harb and Prasad [18] propose an improved variable ordering method to obtain the minimum number of nodes in ROBDD which uses the graph topology to find the best variable ordering. Most recently, a double hybridized genetic algorithm has been proposed in [19] for the optimization of vari- able order in ROBDD. The proposed technique combines a branch & bound technique with the basic genetic algo- rithm and then uses the linear shifting algorithm as the second hybridization to find ROBDD with reduced com- plexity. We can see that variable ordering has been potentially used for reducing the size of OBDDs. In this paper, we propose some efficient variable ordering algorithms, namely, a genetic algorithm based technique and a branch and bound technique. Each of which not only reduces the size of the BDD but at the same time also minimizes power consumption. Section 2 defines the problem with some examples and then Section 3 de- scribes the methodology of adopting the two algorithms with respect to the current problem, followed by results of experimentation. Convergence to global optimum is given in Section 4. Analysis and comparison of results with other techniques are presented in Section 5. Finally, Section 6 draws the conclusion. 2. Defining the Problem of Variable Ordering in BDDs Digital integrated circuits often represented as Boolean functions can be best-manipulated graphically in the form of Binary Decision Diagrams (BDD). A BDD can be expressed mathematically as follows. :,0,fB BB (1) where f is a switching function and π—a total order on a fixed set of Boolean variables x1, x2, ···, xn. An OBDD with respect to order π is a single rooted direct acyclic graph that satisfies the properties as described in [20]. It is already mentioned that the size of a BDD is strongly dependent on the ordering of variables and is also ex- plained in Figure 1. Improving the variable ordering of BDDs is NP- Complete and finding the best order is NP-hard. How- ever, the most tedious job in case of OBDDs is to find an optimal variable order. An optimal variable order has a greater impact on power minimization also, as because, node switching and leakage is dependent on the number of BDD nodes and its order. Majority of the heuristic techniques discussed here has stressed only upon the size or complexity of the resulting BDD. However, power is considered to be one of the critical design issues espe- cially when there is drastic device scaling and increasing use of portable, battery-operated digital devices in recent times. In this paper, due weightage is given to both the area (complexity) and power consumption of the result- ing BDD after optimization. The next section proposes two techniques to tackle the problem of finding optimal variable order in order to minimize BDD complexity (area) and power. (a) (b) Figure 1. The influence of the variable ordering for f(a,b,c,d) = ab + cd with the order a, b, c, d (a) and order a, c, b, d (b). Copyright © 2011 SciRes. CS  S. CHAUDHURY ET AL. 219 3. Proposed Approaches We have attempted two different algorithmic approaches for efficient ordering of variables in OBDD, namely, the genetic algorithm which is an excellent multi-objective optimization technique and a branch and bound optimi- zation approach, which is an exact method. At first, we will put our variable ordering problem in the framework of GA and constitute a GA-based program to obtain the best possible order decided by the minimal node count and power consumption of the resulting BDD. This will be followed by the experimentation with a number of benchmark circuits. The flowchart of Figure 2 shows a pictorial representation of the proposed GA based tech- nique. Next, we will go for the same variable ordering prob- lem by adopting a branch and bound (BB) based greedy algorithmic approach which is also an excellent optimi- zation technique for multi-objective problems and has a finite but usually very large number of feasible solutions. A BB algorithm searches the complete space of solutions (exact method) for a given problem for optimum solution. However, in the current variable ordering problem for optimizing area and power, in combinational logic cir- cuits realized as BDDs, explicit enumeration is normally impossible due to the exponentially increasing number of potential solutions (factorial n number of solutions), so a modified BB algorithm is taken up, the details of which we will see in Section 3.2. Input benchmark ckt terminate Get BDD Reorder Get NC and SA buddy2.4 GA-generated solutions Rank sol(s) Is consistent solution ? Figure 2. Flow-chart of the proposed GA-based technique. 3.1. Genetic Algorithm Based Approach Genetic Algorithms (GA) are stochastic optimization based on principle of natural selection and natural genet- ics. They start with an initial population (solution space) consisting of a set of randomly generated solutions. Based on some reproductive plan especially, the cross- over and mutation, they are allowed to evolve over a number of generations. After each generation, the chro- mosomes are evaluated based on some fitness criteria. Depending upon the selection policy and fitness value, the set of chromosomes for next generation are selected. Finally, the algorithm terminates when there is no im- provement in solution over a fixed number of genera- tions. The best solution at that generation is accepted as the solution produced by GA. The formulation of Genetic Algorithm for any prob- lem involves the careful and efficient encoding of the solutions to form chromosomes, cross-over and mutation operators and a cost function measuring the fitness of the chromosomes in a population. We discuss each of these in subsequent sections. 3.1.1. Solution Representation Here, given a multilevel, multi-output circuit with n number of input (variables), the problem is to find an optimal order and as such the chromosome is a set of n variables (i1, i2, i3, i4, i5, ···, in) of any order with no repe- tition of variables. For example, a combinational logic circuit consisting of 7 variables (inputs) then according to above, 2 3 1 4 5 7 6 is a chromosome, where, each decimal number represents an input (variable) taken in some order. 3.1.2. Genetic Operators Two types of genetic operators namely the crossover and the mutation, are applied to selected parents for generat- ing offspring. Crossover is performed between two se- lected individuals, called parents, by exchanging parts of their features (i.e. encodings) to form two new individual, called offspring. The crossover point is selected ran- domly, and the substrings of two parent chromosomes are exchanged to form the offspring. Care must be taken to see that neither a variable is repeated in a chromosome nor a duplicate chromosome is generated as offspring. To generate better offspring, whole population is sorted ac- cording to fitness value and the best-fit chromosomes take part in crossover. The mutation operator brings variety into population by selecting a chromosome randomly from the popula- tion and modifies the chromosome at a point depending Copyright © 2011 SciRes. CS 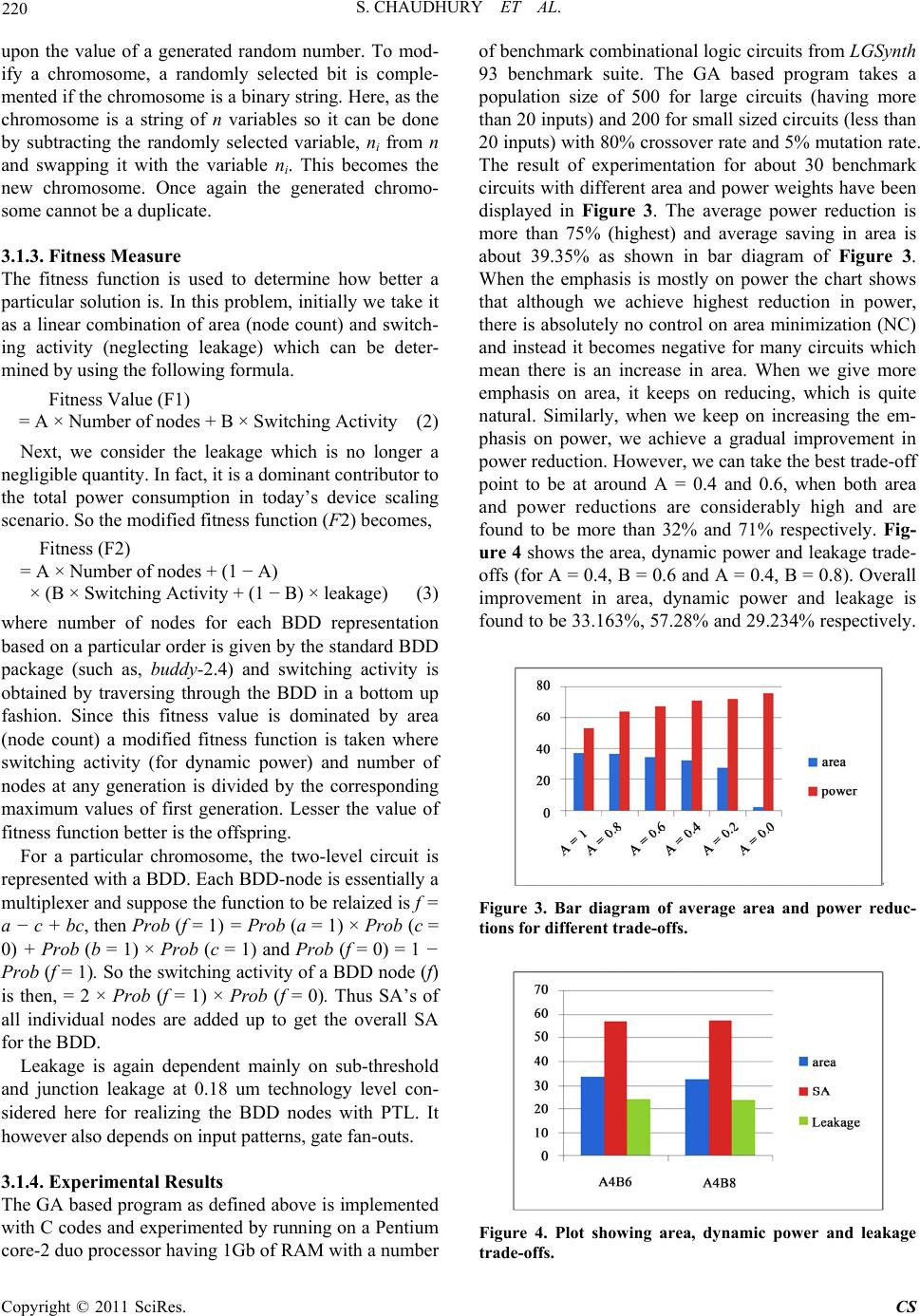 220 S. CHAUDHURY ET AL. upon the value of a generated random number. To mod- ify a chromosome, a randomly selected bit is comple- mented if the chromosome is a binary string. Here, as the chromosome is a string of n variables so it can be done by subtracting the randomly selected variable, ni from n and swapping it with the variable ni. This becomes the new chromosome. Once again the generated chromo- some cannot be a duplicate. 3.1.3. Fitness Mea sure The fitness function is used to determine how better a particular solution is. In this problem, initially we take it as a linear combination of area (node count) and switch- ing activity (neglecting leakage) which can be deter- mined by using the following formula. Fitness Value (F1) = A × Number of nodes + B × Switching Activity (2) Next, we consider the leakage which is no longer a negligible quantity. In fact, it is a dominant contributor to the total power consumption in today’s device scaling scenario. So the modified fitness function (F2) becomes, Fitness (F2) = A × Number of nodes + (1 − A) × (B × Switching Activity + (1 − B) × leakage) (3) where number of nodes for each BDD representation based on a particular order is given by the standard BDD package (such as, buddy-2.4) and switching activity is obtained by traversing through the BDD in a bottom up fashion. Since this fitness value is dominated by area (node count) a modified fitness function is taken where switching activity (for dynamic power) and number of nodes at any generation is divided by the corresponding maximum values of first generation. Lesser the value of fitness function better is the offspring. For a particular chromosome, the two-level circuit is represented with a BDD. Each BDD-node is essentially a multiplexer and suppose the function to be relaized is f = a − c + bc, then Prob (f = 1) = Prob (a = 1) × Prob (c = 0) + Prob (b = 1) × Prob (c = 1) and Prob (f = 0) = 1 − Prob (f = 1). So the switching activity of a BDD node (f) is then, = 2 × Prob (f = 1) × Prob (f = 0). Thus SA’s of all individual nodes are added up to get the overall SA for the BDD. Leakage is again dependent mainly on sub-threshold and junction leakage at 0.18 um technology level con- sidered here for realizing the BDD nodes with PTL. It however also depends on input patterns, gate fan-outs. 3.1.4. Experimental Results The GA based program as defined above is implemented with C codes and experimented by running on a Pentium core-2 duo processor having 1Gb of RAM with a number of benchmark combinational logic circuits from LGSynth 93 benchmark suite. The GA based program takes a population size of 500 for large circuits (having more than 20 inputs) and 200 for small sized circuits (less than 20 inputs) with 80% crossover rate and 5% mutation rate. The result of experimentation for about 30 benchmark circuits with different area and power weights have been displayed in Figure 3. The average power reduction is more than 75% (highest) and average saving in area is about 39.35% as shown in bar diagram of Figure 3. When the emphasis is mostly on power the chart shows that although we achieve highest reduction in power, there is absolutely no control on area minimization (NC) and instead it becomes negative for many circuits which mean there is an increase in area. When we give more emphasis on area, it keeps on reducing, which is quite natural. Similarly, when we keep on increasing the em- phasis on power, we achieve a gradual improvement in power reduction. However, we can take the best trade-off point to be at around A = 0.4 and 0.6, when both area and power reductions are considerably high and are found to be more than 32% and 71% respectively. Fig- ure 4 shows the area, dynamic power and leakage trade- offs (for A = 0.4, B = 0.6 and A = 0.4, B = 0.8). Overall improvement in area, dynamic power and leakage is found to be 33.163%, 57.28% and 29.234% respectively. Figure 3. Bar diagram of average area and power reduc- tions for different trade-offs. Figure 4. Plot showing area, dynamic power and leakage trade-offs. Copyright © 2011 SciRes. CS  S. CHAUDHURY ET AL. 221 It is also observed that the area saving can be as high as 97.33% (with 100% area weight) and power reduction of 97.46% (with 100% power weight) for a large circuit, such as, seq which is quite promising. In fact the benefit of area and power reduction is more for large circuits. 3.2. Branch and Bound Algorithm In this section, we take up the problem of BDD optimi- zation by formulating a branch and bound algorithm (BB). As the target is for an optimal trade-off between area and power, we propose here a greedy search tech- nique using BB for the current variable ordering problem. A BB algorithm searches the whole solution space for the best solution. This is done by an iteration process which has three main components: selection of the solu- tion set for bound calculation, and branching. The se- quence of these may vary according to the strategy cho- sen for selecting the next solution set to process. Here the selection of next solution set is based on the bound value of the solution sets obtained after branching from the previous level. For each of these iterations, it is checked whether the subspace consists of a lower bound, in that case, it is compared with the current best solution thereby retaining the better of the two while pruning the other sets. 3.2.1. Branching Scheme This step is called branching as its recursive application defines a tree structure (the search tree) whose nodes are obtained from the previous level by a splitting procedure i.e. subdivision of the solution space of the nodes into two or more subspaces to be investigated in a subsequent iteration. Since the efficiency of the method depends strongly on the node-splitting procedure and on the lower bound estimators, we start the search from a set of sorted, non-duplicate potential solutions and applied variable’s sequence inversion of a solution and the technique can be categorized as variable appending. Accordingly, we have three different types of solutions space, namely left- side_inverted, rightside_inverted and bothside_inverted. This splitting technique provides maximum non-over- lapping subsets or no overlapping subsets as shown in Figure 5. 3.2.2. Bounding Scheme The next step of the proposed BB technique is a proce- dure that computes only the lower bounds of the so lu- tion_set by calculating the bounds for each of the solu- tions, within the given solution_set. This step is called bounding. The lower bounds are calculated by setting the objective function of the proposed problem based on the fitness as defined in Equations (2) and (3). The key idea of the BB algorithm is: if the lower bound for some tree nodes (set of candidates) A is greater than the lower bound for some other node B in the same level, then A may be safely discarded from the search. This step is called pruning, and is usually implemented by maintain- ing a global variable m (shared among all nodes of the tree) that records the minimum lower bound seen among all solutions examined so far. Any node whose lower bound is greater than m can be discarded. Otherwise, the bounding function for the subspace is calculated and compared with the current best solution. 3.2.3. Termination Criteria The search terminates when we reach Level-(n-2), where n is the number of variables and the optimal solution is then the one recorded as “current best”. Ideally the pro- cedure stops when all nodes of the search tree are either pruned or solved. At that point, all non-pruned sub-re- gions will have their upper and lower bounds equal to the global minimum of the function. To check whether the solution obtained converges to the local minimum or not, we have repeated the above algorithmic steps by starting the search from a different solution set obtained by re- versing the set of Level-1. 3.2.4. Experimentation and Result The proposed BB algorithms is written in C and exhaus- tive experimentation has been done with the same set up as was done for GA based algorithm, with the same set of benchmarks. An input combinational logic circuit is first converted to BDD, the order of which is decided by the proposed algorithm while trading off area and power. The trade off is done by taking different weights for area (node count) and power (switching activities). Simula- tion is carried out for n-2 levels where n is the number of inputs in the circuit. The parameters taken for the ex- perimentation purpose are as follows: 1 = 2 1 3 4 5 6 7 8 10 9 2 = 3 4 2 1 5 6 7 10 9 8 1 A = 1 2 9 10 8 7 6 5 4 3 2 = 4 3 8 9 10 7 6 5 1 2 1 A = 2 1 9 10 8 7 6 5 4 3 2 = 3 4 8 9 10 7 6 5 1 2 L_inv B_inv R_inv Level-1 L-2 A 1 = 1 2 | 3 4 5 6 7 8 10 9 A 2 = 4 3 | 2 1 5 6 7 10 9 8 · · ·· · · · · · Figure 5. Branching scheme. Copyright © 2011 SciRes. CS  222 S. CHAUDHURY ET AL. Solution Set size-50 for large circuits (inputs > 20) and 100 for small and medium circuits (inputs < 20) The weights varies from 0 to 1 (0, 0.2, 0.4, 0.6, 0.8 and 1 are taken in present work). The result of experi- mentation for about 30 benchmark circuits taking differ- ent area and power weights has been shown in Figure 6. It shows the results in terms of percentage improvement in area and power against different weights. As it is clear from the bar diagram that the average power reduction is more than 78% (highest) and average saving in area is about 38.225%. It is also to be noted that even for the area weights A = 0.8 and A = 1.0, there is no negative values of switching activity, which means in almost all circuits there is a reduction in power consumption or zero reduction but no increase in power consumption. When power weight of B = 0.0, area is optimized maxi- mally. Again, when the emphasis is mostly on power the chart shows that although we achieve highest reduction in power, but there is absolutely no control on area minimization (NC). When we give more emphasis on area, saving in power keeps on reducing, which is quite natural. Similarly, when we keep on increasing the em- phasis on power, we achieve a gradual improvement in power reduction. However, we can take the best trade-off point to be at around A = 0.4 and 0.6, when both area and power reductions are considerably high and are found to be more than 30% and 70% respectively. It is also observed that the area saving can be as high as 95.9% ( with 100% area weight) and power reduction of 98.429% (with 100% power weight) for a large cir- cuits, such as, seq and cp s, which is quite promising. In fact, the benefit of area and power reduction is more for large circuits. 4. Convergence of the Approaches In this section we will see the convergence of the pro- posed GA based and BB based approaches towards Figure 6. Bar diagram of average area and power reduc- tions (BB based approach) for different trade-offs. global optimum by framing an exhaustive search pro- gram and running it for a few benchmarks circuits taking all possible input (variable) orders. To minimize CPU time, we have confined our simulations to circuits having variables (inputs) less than 7. When we compare the GA based optimization results with exhaustively searched ones, we find that both GA and BB results in same area reduction for the five benchmarks circuits considered i.e. converges to exhaustive search. However, for power, we find that the convergence is about 1.50% to 4.44% (for A = 0.4 and B = 0.6) to optimum value. Whereas, with BB algorithm, we find the convergence of power is about 1.05% to 9.09% (for different area and power trade-offs) to optimum value. This explains that the GA based ap- proach converges more to the optimum value than the BB based approach, thus indicating the effectiveness of the GA based approach. 5. Comparison of Different Approaches If we observe the results of our GA-based approach and BB approach then we find that the overall results are much better compared to the most binate sort of ordering as shown Table 1. Output phase assignment technique [14] for area and power minimization on the other hand can produce a maximum of 15.72% and 19.18% saving in area and power respectively. While with dynamic variable ordering as proposed in [5] and the hybrid algo- rithm in [9], the average area reduction is as high as 45% and 30%, respectively, compared to the initial value. However they do not take power minimization into ac- count. We then compare the results of the proposed two algorithms, with the most recent heuristic search algo- rithm based on scatter search [15], for some of the benchmark circuits as shown in Table 1. The average results for each of the algorithms in terms of percentage improvement in area are shown in the last row of Table 1. We can see that the modified BB algo- rithm and the GA based algorithm will be a better option when the area reduction is given the highest priority, while the scatter search approach will be preferable from the point of view of minimal computational time com- plexity (of the order of 0.053 hr) as shown in Figure 7. 6. Conclusions Presented here two techniques for BDD optimization namely, GA based optimization and Branch and Bound based Greedy optimization. Exhaustive experimentation has been done with ISCAS93 benchmark circuits to see the effectiveness of the proposed two techniques for area and power optimization. Finally, the comparison with other established techniques such as, scatter search tech nique and dynamic variable ordering have been done and Copyright © 2011 SciRes. CS 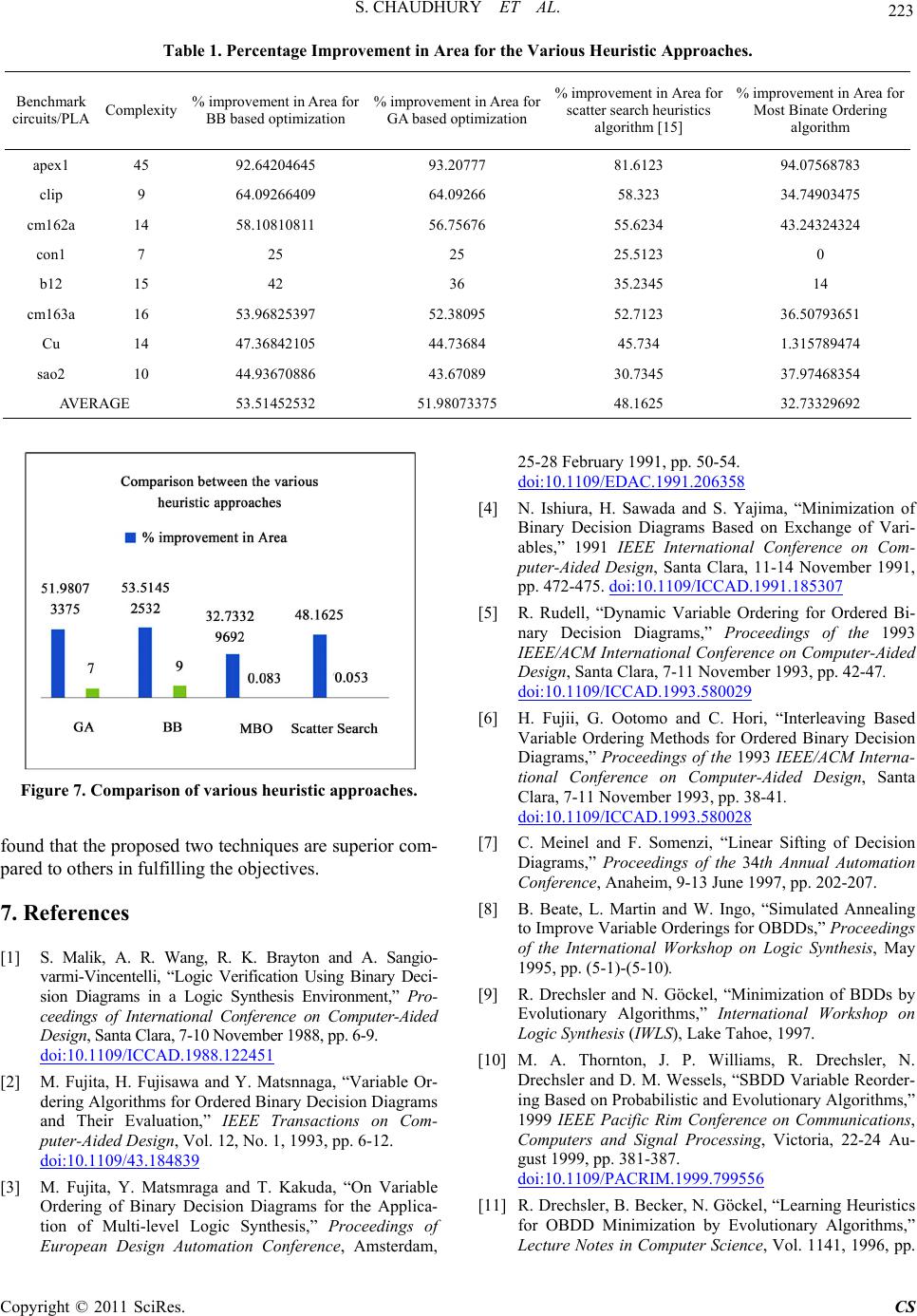 S. CHAUDHURY ET AL. Copyright © 2011 SciRes. CS 223 Table 1. Percentage Improvement in Area for the Various Heuristic Approaches. Benchmark circuits/PLA Complexity % improvement in Area for BB based optimization % improvement in Area for GA based optimization % improvement in Area for scatter search heuristics algorithm [15] % improvement in Area for Most Binate Ordering algorithm apex1 45 92.64204645 93.20777 81.6123 94.07568783 clip 9 64.09266409 64.09266 58.323 34.74903475 cm162a 14 58.10810811 56.75676 55.6234 43.24324324 con1 7 25 25 25.5123 0 b12 15 42 36 35.2345 14 cm163a 16 53.96825397 52.38095 52.7123 36.50793651 Cu 14 47.36842105 44.73684 45.734 1.315789474 sao2 10 44.93670886 43.67089 30.7345 37.97468354 AVERAGE 53.51452532 51.98073375 48.1625 32.73329692 Figure 7. Comparison of various heuristic approaches. found that the proposed two techniques are superior com- pared to others in fulfilling the objectives. 7. References [1] S. Malik, A. R. Wang, R. K. Brayton and A. Sangio- varmi-Vincentelli, “Logic Verification Using Binary Deci- sion Diagrams in a Logic Synthesis Environment,” Pro- ceedings of International Conference on Computer-Aided Design, Santa Clara, 7-10 November 1988, pp. 6-9. doi:10.1109/ICCAD.1988.122451 [2] M. Fujita, H. Fujisawa and Y. Matsnnaga, “Variable Or- dering Algorithms for Ordered Binary Decision Diagrams and Their Evaluation,” IEEE Transactions on Com- puter-Aided Design, Vol. 12, No. 1, 1993, pp. 6-12. doi:10.1109/43.184839 [3] M. Fujita, Y. Matsmraga and T. Kakuda, “On Variable Ordering of Binary Decision Diagrams for the Applica- tion of Multi-level Logic Synthesis,” Proceedings of European Design Automation Conference, Amsterdam, 25-28 February 1991, pp. 50-54. doi:10.1109/EDAC.1991.206358 [4] N. Ishiura, H. Sawada and S. Yajima, “Minimization of Binary Decision Diagrams Based on Exchange of Vari- ables,” 1991 IEEE International Conference on Com- puter-Aided Design, Santa Clara, 11-14 November 1991, pp. 472-475. doi:10.1109/ICCAD.1991.185307 [5] R. Rudell, “Dynamic Variable Ordering for Ordered Bi- nary Decision Diagrams,” Proceedings of the 1993 IEEE/ACM International Conference on Computer-Aided Design, Santa Clara, 7-11 November 1993, pp. 42-47. doi:10.1109/ICCAD.1993.580029 [6] H. Fujii, G. Ootomo and C. Hori, “Interleaving Based Variable Ordering Methods for Ordered Binary Decision Diagrams,” Proceedings of the 1993 IEEE/ACM Interna- tional Conference on Computer-Aided Design, Santa Clara, 7-11 November 1993, pp. 38-41. doi:10.1109/ICCAD.1993.580028 [7] C. Meinel and F. Somenzi, “Linear Sifting of Decision Diagrams,” Proceedings of the 34th Annual Automation Conference, Anaheim, 9-13 June 1997, pp. 202-207. [8] B. Beate, L. Martin and W. Ingo, “Simulated Annealing to Improve Variable Orderings for OBDDs,” Proceedings of the International Workshop on Logic Synthesis, May 1995, pp. (5-1)-(5-10). [9] R. Drechsler and N. Göckel, “Minimization of BDDs by Evolutionary Algorithms,” International Workshop on Logic Synthesis (IWLS), Lake Tahoe, 1997. [10] M. A. Thornton, J. P. Williams, R. Drechsler, N. Drechsler and D. M. Wessels, “SBDD Variable Reorder- ing Based on Probabilistic and Evolutionary Algorithms,” 1999 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Victoria, 22-24 Au- gust 1999, pp. 381-387. doi:10.1109/PACRIM.1999.799556 [11] R. Drechsler, B. Becker, N. Göckel, “Learning Heuristics for OBDD Minimization by Evolutionary Algorithms,” Lecture Notes in Computer Science, Vol. 1141, 1996, pp.  224 S. CHAUDHURY ET AL. 730-739. doi:10.1007/3-540-61723-X_1036 [12] W. Günther and R. Drechsler, “Improving EAs for Se- quencing Problems,” Proceedings of the Genetic and Evolutionary Computation Conference, 2000. [13] R. Drechsler, M. Kerttu, P. Lindgren and M. Thornton, “Low Power Optimization Techniques for BDD Mapped Circuits Using Temporal Correlation,” Canadian Journal of ECE, Vol. 27, No. 4, 2002, pp. 159-164. [14] S. Chaudhury and S. Chattopadhyay, “Output Phase As- signment for Multilevel Multi-output Logic Synthesis with Area and Power Trade-offs,” 2006 Annual IEEE In- dia Conference, New Delhi, 15-17 September 2006, pp, 1-4. [15] W. N. N. Hung, X. Song, E. M. Aboulhamid and M. A. Driscoll, “BDD Minimization by Scatter Search,” IEEE transactions on Computer-Aided Design of Integrated Circuits and Systems, Vol. 21, No. 8, 2006, pp. 974-979. [16] P. W. C. Prasad, M. Raseen, A. Assi and S. M. N. A. Senanayake, “BDD Path Length Minimization Based on Initial Variable Ordering”, Journal of Computer Science, Vol. 1, No. 4, 2005, pp. 520-528. [17] M. Rice and S. Kulhari, “A Survey of Static Variable Ordering Heuristics for Efficient BDD/MDD Construc- tion,” Technical Report, 2008. http://www.cs.ucr.edu/~skulhari/StaticHeuristics.pdf [18] P. W. C. Prasad, A. Assi, A. Harb and V. C. Prasad, “Bi- nary Decision Diagrams: An Improved Variable Ordering using Graph Representation of Boolean Functions,” In- ternational Journal of Computer Science, Vol. 1, No. 1, 2006, pp. 1-7. [19] O. Brudaru, R. Ebendt and I. Furdu, “Optimizing Vari- able Ordering of BDDs with Double Hybridized Embry- onic Genetic Algorithm,” Proceedings of 12th IEEE In- ternational Symposium on Symbolic and Numeric Algo- rithms for Scientific Computing, Timisoara, 23-26 Sep- tember 2010, pp. 167-173. [20] R. Ebendt, F. Gorschwin and R. Drechsler, “Advanced BDD Minimization”, Springer, New York, 2005. Copyright © 2011 SciRes. CS
|