Received October 2015

ABSTRACT

This article introduces a hyper-exponential jump diffusion process based on the continuity correction for discrete barrier options under the standard B-S model, using measure transformation and stopping time theory to prove the correction, thus broadening the conditions of the continuity correction of Kou.

Keywords:

B-S Model, Discrete Barrier Options, Hyper-Exponential Jump Diffusion, Continuity Correction Formula

1. Introduction

In 2003, S. G. Kou [1] generalized a double exponential jump diffusion model into the pricing of continuity single barrier options. They analyzed the joint distribution of the final asset price by focusing on first passage time and combining it with the nonlinear renewal theory of the time series analysis. The Laplace transforms and the non-memory property of exponential distribution were also used during the analyzing process. In his article which was published in 1997, Kou [2]-[4] put forward a continuity correction of B-S model, which combined the pricing method of continuity barrier options with that of discrete barrier options. In 2013, D. Jun [5] generalized the continuity correction formula into the double barrier options in view of Kou’s report. Also in 2013, C. D. Fuh [6] introduced the double exponential jump diffusion model to the pricing of discrete single barrier options and look-back options. His article widened the conditions of the continuity correction formula of Kou and obtained a correction formula of discrete barrier options based on the double exponential jump diffusion process.

This article uses Kou’s theoretical derivation method for the first passage time and C. D. Fuh’s thought of proving the correction formula based on double exponential jump diffusion model for reference. In order to generalize the model into the pricing of both the discrete single and double barrier options on the basis of the hyper-exponential jump diffusion process, we combine the correction formula of discrete single barrier options raised by Kou with D. Jun’s correction of discrete double barrier options under the B-S model. Although formally, the correction formula in this article seems to be same as Kou’s and D. Jun’s, there are no restrictions of strike price K and barrier value H in the correction formula in this passage, which means that the scope of application of Kou’s and D. Jun’s correction are widened. Additionally, compared with the double exponential jump diffusion model of C. D. Fuh, the hyper-exponential jump diffusion model in this article is more general.

2. Pricing on Barrier Options

2.1. Continuity Correction Model

In 1997, Steven Kou put forward the concept of continuity correction in his paper, which combined the continuity barrier options with the discrete barrier options through the continuity correction formula. Denote the stopping time by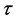, the definition goes as follows:

(2.1)

or

(2.2)

Here H stands for the barrier level and is the frequency of monitoring. Formula (2.1) and (2.2) represent the situation of continuously monitored and discretely monitored, respectively. Apparently, an up model has 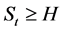and a down model has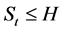. For convenience, we assume the risk-neutral interest rate r is a constant in this case. Because of the existence of jump, the “market” here is not a complete market, which means that the risk neutrality measure is not unique (more details can be found in Kou [7]). As a matter of convenience, we assume the risk neutrality measure Q just needs to meet the premise of rational expected equilibrium.

Kou has pointed out in his article that when m is large enough, which means, Formula (2.2) is weakly convergent to Formula (2.1). However, with the increasing of m, the convergence rate will become very slow and the error will also increase. To solve this problem, Kou implemented methods of time series analysis, which could provide limitations of K and H, and established correction formula as follow, based on the B-S model to fasten the convergence rate:

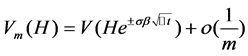(2.3)

If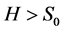, “+” will be applied, if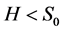, “−” will be applied.

Here, 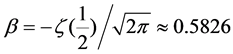, with 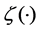standing for Riemann zeta function, which can be concretely written as.This method of adjustment is called continuity correction.

According to the correction formula, we could find that the barrier-crossing probability will be lower after the adjustment of discretely monitored barrier. The amount of the adjustment is.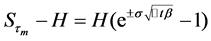

2.2. Hyper-Exponential Jump Diffusion Model

We assume that under the risk neutrality measure Q, the asset price 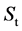will obey the following hyper-expo- nential jump diffusion geometric Brownian motion model:

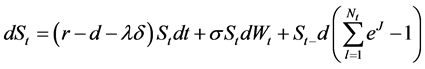(2.4)

(2.5)

Here is a standard Brownian motion, is a Poisson process with intensity, stands for the underlying asset price at previous moment, and constant represent the risk-free interest

rate, dividend rate and risk volatility, respectively. is a sequence of independent identically distributed random variables, ,

.

(2.6)

Using Ito lemma and theories of calculation of stochastic partial differential equations, the solution of model (2.4) under continuously monitored situation is:

(2.7)

where, and.

It’s obvious that, when we assume the discretely monitored time interval is, the discretely monitored asset price is, at the nth time of monitoring. As a result,

(2.8)

where,. All random variables here are independent. Now we suppose is the algebra, consequently, will still be a Q-martingale. Take the continuous up-in-put options for example, the option return is, and the corresponding discrete situation is. We use to replace for more explicit expression. Therefore, equations (2.1), (2.2) could be written as:

(2.9)

where.

Now we try to find the relationship between this two joint distribution densities, and. For (2.7) and (2.8), define,. According to the Lévy-Khintchine formula, the characteristic function can be expressed as

(2.10)

Let be the corresponding characteristic function of jump size J, and the cumulative generating function is (namely). Therefore,

(2.11)

For convenience, we use and to replace and, respectively. Denote, and now we provide the corresponding Laplace transform.

Proposition 2.1. [8] For hyper-exponential jump diffusion model (2.4) and (2.5), when, for, the Laplace operator of stopping time can be written as follows:

(2.12)

where is uniquely determined by linear equations , ,..

. What’s more,. In view of proposition 2.1, we can obtain the probability distribution of is

(2.13)

2.3. Pricing on Discrete Single Barrier Options

In this section, based on the discrete model (2.8), firstly, we make an adjustment on the discrete model, denote, then `. As a result,

and,

where. So we can have.

The preparation has been done, however, two preparatory lemmas will be introduced before finally exhibit the main conclusion.

Lemma 2.2. For continuously monitored stopping time, discretely monitored stopping time (Formula (2.9)), maturity T and monitoring time interval, when, the following equation is satisfied for arbitrary constant:

(2.14)

Proof: Assume (2.14) is a true statement, in view of (2.12) and (2.13), when,

(2.15)

From proposition 2.1, the equation above will be true if the following equation is proved:

(2.16)

where. To prove this formula, for an arbitrary constant b > 0 and constant h > 0, define a function, satisfy, which can be written as :

(2.17)

In order to obtain Equation (2.15), here, we solve this problem by adjusting Kou’s method of the first passage time under the double exponential jump diffusion process. Noticing that

(2.18)

where L stands for the infinitesimal generator

(2.19).

Here, is supposed to be twice continuously differentiable. For, we use formula to construct a series of function, As a result, for, there are. Then combining (2.18) and (2.19), for all,

As, for all,

(2.20)

where. And because is a constant, we can obtain that

(2.21)

Focusing on, we implement formula and combine (2.21), for,

(2.22)

is the local martingale and. According to the definition, there are a series of stopping time and as well. Therefore, for every, is a martingale. And according to Lebesgue’s dominated convergence theorem,

more precisely,

,

and in view of (2.21)

.

If we integrate the three formulas above, for all,

,

Now for convenience, is used to replace. Based on Kubilius [9], let, when,

As and are asymptotically independent, when,

(2.23)

which obeys Taylor expansion of the first order and. Here we use Kou’s treatment of for reference and define random walk

and

When,

(2.24)

Lemma 2.2 can be proved by substituting (2.24) and (2.16) into (2.15).

Lemma 2.3. For discrete barrier options with times of monitoring and value of barrier H, there are stopping time, (for convenience, denote), and their corresponding logarithm underlying asset prices, (Formula (2.8)). For (Formula (2.11)), the joint distribution and meet the following equation:

(2.25)

where.

Proof:

On the basis of proposition 2.1 in Kou [1] and Zhang [10], and are asymptotically independent, denote.

When, ,

Therefore,

(2.26)

Then lemma 2.3 can be proved by using corollary 3.3 in Kou [4].

Theorem 2.1. Let denote the price of continuously monitored options with barrier value H, accordingly, is the price of discretely monitored options with the monitoring frequency. Consequently, for an arbitrary discrete barrier option with maturity T, , and when, we obtain the following correction formula:

(2.27)

where, with the Riemann zeta function.

The proof of the theorem can be derived directly from Lemma 2.2 and 2.3. What we need to illustrate is that although the conclusion here seems to be similar to Kou [2]’s, there are no restriction of (upward) and (downward) for the striking price K and barrier H.

Cite this paper

Ting Liu,Chang Feng,Yanqiong Lu,Bei Yao, (2015) A Note on the Kou’s Continuity Correction Formula. Open Journal of Social Sciences,03,28-34. doi: 10.4236/jss.2015.311005

References