Received October 2015

ABSTRACT

Discovering complex and incomplete periodic patterns in the logs of events is a complicated and time consuming task. This work shows that it is possible to discover complex and incomplete periodic patterns through finding simple patterns first and through logical derivations of complex and incomplete patterns later on. The paper defines a syntax and semantics of a class of periodic patterns that frequently occur in the logs of events. A system of derivation rules proposed in the paper can be used to transform a set of periodic patterns into a logically equivalent set of patterns. The rules are used in the algorithms that derive complex and incomplete periodic patterns. A prototype implementation of the algorithms that discover complex and incomplete periodic patterns in the logs of events is presented.

Keywords:

Periodic Pattern, Complex Periodic Pattern, Incomplete Periodic Pattern, Derivation Rules, Data Mining Algorithms

1. Introduction

It is well known that precise estimation of the future workloads can be used to eliminate many performance related problems in database systems [1]. When the future operations on a database are known to a database administrator then it is possible to apply database performance tuning techniques such as indexing, clustering, partitioning of data containers, caching, relocation of data containers to faster persistent storage devices, materialization of the results of expected computations and the others. It is also well known that workload characteristics periodically change due to the repetitive nature of the real world processes implemented by in the database systems. Therefore, information about the workloads recorded in the past can be analyzed in order to anticipate the workloads in the future. The characteristics of database workloads can be quite easily collected at run-time and it can be saved in a form of log, audit trail, processing traces, etc. Unfortunately detection of the periodic changes in the workloads is a difficult problem due to the large amounts of collected data and due to a high level and nondeterministic nature of the periodically repeated processes [2]. A single process may consist of hundreds of events and it may overlap in time with many other processes. Additionally, periodicity of the processes may be incomplete due to the random events as well as due to the slight differences in length of the adjacent periods.

A problem of finding periodic patterns in the recorded workloads can be solved in a different way from the computationally intensive generation of candidate patterns and their subsequent verification in the logs of events. An important property of periodically repeated processes says that no matter how long and how complex a process is, all its elementary operations are also processed periodically. It leads to an idea where discovery of complex and incomplete periodic patterns can be done through discovery of periodic patterns of individual operations and later on through composition of simple patterns into the complex and incomplete ones. Discovery of simple and complete periodic patterns based on one operation or event can be done in a relatively simple way after partitioning historical data into the subsets that record activities of only one operation or event. The outcomes are the elementary and complete periodic patterns. Then, such homogeneous and complete patterns are “stitched” into the homogeneous and incomplete patterns with certain predefined maximum number of cycles missing. In the next stage, the sets of homogeneous and incomplete periodic patterns are union and all pairs of patterns that satisfy the predefined composition constraints such as minimal length, maximal carrier length are created and composed into complex and incomplete periodic patterns. The procedure is repeated until no new pairs can be found.

To implement a method described above we need a system of derivation rules that transforms the sets of periodic patterns into the logically equivalent sets of patterns and that allows for synthesis of longer patterns and composition of more complicated patterns. The main objective of this paper is to propose a system of derivation rules for complex and incomplete periodic patterns and to show how such system can be used in the algorithms and in a simple prototype implementation that discovers the incomplete periodic patterns from the logs of event.

The paper is organized in the following way. The next section reviews the previous research works related to discovering periodic patterns in historical information. Section 3 defines the concepts of multisets, time units and it shows how a log of events is transformed into a workload trace. Section 4 defines the syntax and semantics of complete and incomplete periodic patterns. A system of derivation rules for incomplete periodic patterns of is proposed in Section 5. Section 6 presents the algorithms that apply the system of derivation rules to find complex and incomplete periodic patterns. Section 7 describes a prototype implementation of the algorithms. Finally, Section 8 concludes the paper.

2. Previous Work

The works on frequent episodes [3] and its extensions on mining complex episodes [4] inspired the works on cyclic patterns. A starting point to many research studies on discovering cyclic patterns is a work [5] that defines the principle concepts of cycle pruning, cycle skipping, cycle elimination heuristics. Discovering periodic patterns in event logs appears to be quite similar to periodicity mining in time series [6] where the long sequences of elementary data items partitioned into a number of ranges and associated with the timestamps are analyzed to find the cyclic trends. The latest works on discovering periodic patterns address the concepts of full periodicity, partial periodicity, perfect and imperfect periodicity [7] and the most recently asynchronous periodicity [8] and [9]. A class of periodic patterns considered in this paper is a variation of periodic patterns earlier investigated in [10] and [11].

3. Workload Trace

Let be a unique identifier of an event, for example identifier of query processing plan in a database system, or an identifier of flight booking routine in a flight reservation system, etc. A log of events is a sequence of pairs 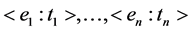where each 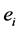is a unique identifier of an event, 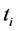is a timestamp when the processing of an event 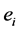has started, and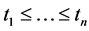.A definition of a workload trace is based on a concept of multiset [12]. A multiset M is a pair 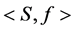where S is a finite set and 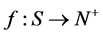is a function such that 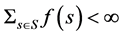called as a cardinality and denoted by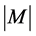. Let 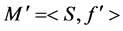be a multiset on S, then we say that 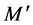is a submultiset of M and we denote it by 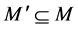if 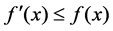for all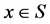. In the rest of this paper we shall denote a multiset 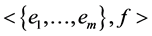where 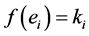for as We shall denote an empty multiset as and we shall abbreviate a single element multiset as.

At a data preparation stage a log of events is transformed into a workload trace in the following way. A period of time over which a log of events is recorded is divided into a sequence U of n disjoint time units where is a timestamp when a time unit starts and is a length of the unit. All time units satisfy the following properties: and and. Let n be the total number of time units in U and let denotes the i-th time unit in U where i changes from 1 to n. A workload trace of an event e is a sequence of n multisets of events such that or for and equal to the total number of times processing of an event e started in the i-th time unit. Let E be a set of all events whose occurrences are recorded in a log over time units U and saved

in a reduced event table. A workload trace of a log is denoted by and, i.e. it is a multiset union over the respective time units of workload traces of all events included in .

4. Periodic Patterns

In this work we consider periodic patterns that belong to a wider class of CRP periodic patterns defined as a triple whose individual components have the following meanings.

Ÿ A carrier C defines a structure of periodically repeated events, computations, queries, etc.

Ÿ A range R determines a time scope of periodic repetitions of a carrier measured in time units, for example from one time unit to another or starting in a given time unit and continuing over several cycles.

Ÿ A periodicity P determines location of the next cycle of periodic pattern, for example after a given number of time units from the latest cycle with possible delay by one or more time units.

In the previous works, for example in [10], a carrier C is a nonempty, finite sequence of multisets of syntax trees of relational algebra expressions implementing SQL statements, a range R is a pair of the ordinal numbers of time units, and a periodicity P is a total number of time units between two adjacent cycles. In [11] a carrier C is defined as a multiset of an event e, R is defined as a pair of numbers that determine the first and the last repetition of a carrier and P is defined as a pair of numbers that determine the minimal and maximum distance between any two adjacent repetitions of a carrier.

In this work we consider a subclass of CRP periodic patterns defined as a triple whose individual components have the following meanings.

Ÿ A carrier C is a nonempty sequence of at least one nonempty multisets of events.

Ÿ A range is a pair of natural numbers where f determines a location of the first cycle and t is the total number of cycles in the pattern.

Ÿ A periodicity is a pair of natural numbers where p determines a period of a cycle, i.e. a distance between every two adjacent cycles and g determines the longest gap between the adjacent cycles, i.e. the maximum total number of adjacent cycles that can be missing from the pattern.

Ÿ The values of and must satisfy the conditions and and and and and and if then and or.

Ÿ If then a periodic pattern is called as a complete periodic pattern otherwise if it is called as an incomplete periodic pattern.

Ÿ It is possible, that, i.e. the largest total number of missing cycles is equal to the total number of cycles in the pattern. Such a “ghost” periodic pattern can be interpreted as information about planned periodical processing of events, which actually has never been implemented and such that it is still possible in the future.

The following sequence of definitions leads to validation of periodic pattern in a workload trace. Let C be a sequence of multisets where. A trace of carrier C spanning over n multisets and starting at a time unit f where is denoted by and it is defined as sequence of empty multisets followed by a sequence of multisets C and followed by empty multisets. For example, is a sequence of multisets.

A trace of a complete periodic pattern over n time units where is denoted by and it is defined as a multiset union of traces for, i.e.. In the other words, a trace of

a complete periodic pattern is a union of traces of its carrier over n multisets such that each trace starts at the time units. For example, a trace of periodic pattern over 5 time units is the following union of sequences of multisets. In a special case when a value of, i.e. when a pattern consists of only one cycle, the values of parameters p and g must be equal to for example, a trace of periodic pattern over 5 time units is equal to. In another case when the values of parameters p and g are equal to and a value of parameter, a trace of periodic pattern over 5 time units is equal to.

A trace of an incomplete periodic pattern over n time units where is denoted by and it is defined as a multiset union of traces for some of and such that the traces are missing from the multiset union.

An incomplete periodic pattern is valid in a workload histogram recorded over n time units if for. Of course a complete periodic pattern is valid in a workload histogram recorded over n time units if for. In the other words a periodic pattern is valid in a workload trace that spans over n time units if some of the elements of its trace over n time units are included in the respective elements of a workload and it never happens that the elements of its trace that are not included in a workload form a contiguous sequence longer than g elements, i.e. the gaps in the cycles are no longer that g.

For example, a periodic pattern is valid in a workload trace because every element of its trace is included in the respective element of the workload trace. The periodic pattern is not valid in a workload trace because an element of its trace is not included in. However, an incomplete periodic pattern is valid in a workload trace because a sequence of at most one contiguous elements of its trace is not included in the workload.

5. Derivation Rules

A system of derivation rules presented below allows for creation of new periodic patterns valid in a workload trace that spans over n time units from a set of periodic patterns already valid in.

5.1. Discovery Rule

Let C be a multiset of events such that for. Then, a periodic pattern is valid in. A discovery rule creates a single cycle periodic pattern valid in from any non-empty submultiset of an element in a workload trace.

5.2. Incompleteness Rule

If a periodic pattern is valid in a workload then a periodic pattern such that is valid in. An incompleteness rule increases the maximum size of gaps acceptable for a periodic pattern.

5.3. Normalization Rule

If a periodic pattern is valid in a workload then a periodic pattern such that is obtained from C through elimination of all i leading empty multisets and all trailing empty multisets and such that is valid in. Normalization rule allows for elimination of leading and/or trailing empty multisets from a carrier of a periodic pattern.

5.4. Split Rule

If a periodic pattern is valid in a workload then the following three cases are possible.

Ÿ If then the periodic patterns and are valid in a workload trace .

Ÿ If and then the periodic patterns and are valid in a workload trace or the periodic patterns and are valid in a workload trace.

Ÿ If and for then the periodic patterns and are valid in a workload trace.

The first case of a split rule divides a pattern that consists of two cycles into two single cycle patterns. The second case “cuts of” a single cycle periodic pattern from either left or right side of a pattern that consist of more than two cycles. Finally, the last case splits a periodic pattern that has more than three cycles into two patterns with more than one cycle.

5.5. Synthesis Rule

If the periodic patterns and are valid in a workload trace and then the following four cases are possible.

Ÿ If and then a periodic pattern is valid in a workload trace.

Ÿ If and and then a periodic pattern is valid in a workload trace.

Ÿ If and and then a periodic pattern is valid in a workload trace.

Ÿ If and and and then a periodic pattern is valid in a workload trace.

In the first case of a synthesis rule merges two single cycle pattern into one pattern. In the next two cases a single cycle pattern is added at the left/right end of another pattern. The last case concatenates two patterns such that both of them consist of more than one cycle.

5.6. Decomposition Rule

If a periodic pattern is valid in a workload trace then a periodic pattern where a carrier is obtained by elimination of any multiset from any element of a carrier C is valid in. For example, if a periodic pattern is valid in then a periodic pattern obtained through the elimination from the first element and from the second element of a carrier is valid in. Then, a normalization rule can be used to eliminate a leading empty multiset from a carrier to get.

5.7. Composition Rule

If the periodic patterns and are valid in a workload trace and then a periodic pattern where is valid in. For example, if the periodic patterns and are valid in a workload trace then a periodic pattern is valid in.

6. Discovering Periodic Patterns

A process of discovering periodic patterns in the workload traces is implemented through systematic application of the derivation rules. In each step the rules transform a set of periodic patterns into an equivalent set of patterns. The objectives of the transformations are to find the periodic patterns that have complex carriers, that are long, that have short periods, and that have smallest length of gaps allowed.

We say that a periodic pattern is homogeneous when its carrier C is a sequence of multisets that contains occurrences of only one and always the same event. The concept of homogenous periodic pattern given above is generalization of [13]. In the first stage we discover and we transform only homogenous periodic patterns. In the second step the sets of homogeneous periodic patterns are combined into complex and incomplete patterns.

The process is controlled by the values of parameters that determines the maximal length of any periodic pattern discovered, that determines the longest gap allowed for a periodic patterns, , that determines the shortest periodic patterns allowed, and that determines the longest possible length of carrier for any periodic patterns found.

6.1. Discovering Homogeneous Periodic Patterns

A process of finding homogeneous periodic patterns consist of four steps in which the derivation rules are applied to a workload partitioned into n workloads. Each, contains only occurrences of an event for extracted from. We repeat the following steps for each.

Step 1

We start from the application of discovery rule to to create the single cycle and complete periodic patterns like.

Step 2

For each we use a synthesis rule to find the longest complete periodic patterns consistent with a form. Then, for all patterns that have the same values of parameters f and t we apply a composition rule to create the patterns like.

Step 3

The split and composition rules are used to transform the patterns like and such that into single cycle pattern where a carrier C is equal to is a sequence of separated with empty sets and repeated times and ended with. A synthesis rule is applied to assemble the single cycle complete periodic patterns into multicycle complete patterns. For example, the patterns, , are first grouped into, , and and later on are synthesized into.

Step 4

Finally, we apply a synthesis rule to the periodic patterns created so far in order to create longer and incomplete patterns with the length of gaps limited by a value of parameter. The rule is iteratively applied for the pairs of periodic patterns that have the same carrier. A pair of periodic patterns that can be synthesized into a longer and incomplete one is replaced with the results of synthesis rule. At the end of this process we obtain n sets of homogenous and incomplete periodic patterns one set per each one of n events recorded in a workload trace.

Complexity of the algorithm depends on the length n of a workload trace, on the maximum period size and on the total number h of homogeneous patterns discovered in the first three steps. The complexity of the first there steps is the complexity of Step 4 is.

6.2. Discovering Complex Periodic Patterns

A process of finding complex periodic patterns initially applies a composition rule to the sets of homogeneous and incomplete patterns obtained in the previous steps. Then, a composition rule is applied to the results of compositions until no new complex and incomplete patterns can be derived. The process is limited by a threshold value that determines the longest possible carrier of periodic pattern obtained from application of a composition rule, by a threshold value. The process is also limited by the maximal allowed length of “gaps” and the minimal length of the results of composition. The following two steps are repeated until no more new periodic patterns can be created with a composition rule.

Step 1

The sets of homogenous and incomplete periodic patterns are assembled into

Step 2

Next, we find in G all pairs of periodic patterns and such that and and and. Then if we apply a split rule to adjust the length of the patterns. A new pattern obtained from a split is appended to G. Additionally each periodic pattern must be a member of at most one pair. If a periodic pattern is involved in more than one pair then we pick a pair that maximizes the length of the patterns obtained from the future composition. It may happen that it is impossible to find any pair of periodic patterns that satisfy the conditions listed above. Then, we end the process of creating complex and incomplete periodic patterns.

Step 3

For each pair of periodic patterns and found in the previous step we apply a composition rule to create a new periodic pattern. Then, we replace the composed patterns in G with the result of composition. When all pairs are processed we return to Step 2.

The complexity of the algorithm is equal to where h is the total number of patterns included in an input set G and k is the total number of patterns obtained from split in Step 2 of the algorithm.

7. Prototype Implementation

The algorithms described in the previous section are implemented in an environment of a commercial relational database management system. We save an audit trail from processing of a sequence of SQL statements against a sample TPC-H benchmark database. Then, we apply EXPLAIN PLAN statement to transform each SQL statement into an expression of extended relational algebra. The computations of individual relational algebra operations are considered as individual events in a log. Suchlog of events together with the times tamps is transformed into a workload trace where the individual operations are grouped within predefined time units. A synthetic workload generator is used to implement periodic processing of sequences of SQL statements. A number of casually processed SQL statements are incorporated into the workload to evaluate an impact of randomly processed statements on discovery of periodic patterns. All software is implemented in SQL embedded into a host language of a database management system used.

Application of a synthetic workload generator allows for precise estimation of the quality of results obtained from the algorithms through the comparison of pre-programmed iterative processing of SQL statements with the periodic patterns obtained from the algorithms. The algorithms are applied several times to the same log of events partitioned each time into the time units of different size. In all cases when a period of iterative processing of SQL statement is a multiplicity of the length of time units the algorithms return almost perfect results and are able to precisely detect the expected patterns. In the cases when a period of iteratively processed sequence of SQL statements was not consistent with the length of time units the algorithm return a larger number of shorter and simpler periodic patterns than expected, however the results were still within the acceptable quality range. Quality of the results also strongly depends on a careful choice of the parameters that restrict carrier length, period length etc. Selection of too large or too small configuration parameters contributes to identification of accidental patterns not planned within a synthetic workload.

8. Summary and Future Work

This work describes a new approach to discovery of complex and incomplete periodic patterns in the logs of events. The method is based on an idea that it is possible to create complex and incomplete periodic patterns through systematic discovery, transformation, and composition of the simpler patterns. The new approach requires a system of derivation rules for transformation of periodic patterns into the equivalent ones. Such system of rules is defined in the paper. We show how the rules can be applied in the algorithms that process a workload trace obtained from a log of events into initially simple and homogeneous patterns and later on into complex and incomplete ones. A prototype implementation of the algorithms is used to discover the periodic patterns among the events equivalent to the computations of individual extended relational algebra operations implementing SQL statements processed by a relational database system.

A number of interesting research problems remain to be solved. An important problem is an appropriate choice of time units used to partition a log of events into multisets of events in a workload trace due an observation that quality of the discovered patterns depends on the length of time units. The next interesting problem includes investigations on the other system of derivation rules that may lead to more efficient implementations. An interesting task is more efficient and more general implementation of the algorithms that can be used to discover periodic patterns in many other domains. Finally, a class of periodic patterns considered in the paper can be extended on the patterns with more sophisticated specification of period parameter allowing for slight variations from cycle to cycle.

Cite this paper

Janusz R. Getta,Marcin Zimniak, (2015) Discovering Complex Incomplete Periodic Patterns through Logical Derivations. Open Journal of Social Sciences,03,8-15. doi: 10.4236/jss.2015.311002

References