Received October 2015

ABSTRACT

In this work, the modeling and stability problem for a communication network system is addressed. The communication network system consists of a transmitter which sends messages to a receiver. The proposed model considers two possibilities. The first one, that messages are successfully received, while in the second one, during the sending process the transmitter breaks down and as a result the message does not reach the receiver. Timed Petrinets is the mathematical and graphical modeling technique utilized. Lyapunov stability theory provides the required tools needed to aboard the stability problem. Employing Lyapunov methods, a sufficient condition for stabilization is obtained. It is shown that it is possible to restrict the communication network system state space in such a way that boundedness is guaranteed. However, this restriction results to be vague. This inconvenience is overcome by considering a specific recurrence equation, in the max-plus algebra, which is assigned to the timed Petri net graphical model.

Keywords:

Communication Network System, Transmitter Breakdown, Discrete Event Dynamical Systems, Max-Plus Algebra, Lyapunov Method, Timed Petri Nets

1. Introduction

In this work, the modeling and stability problem for a communication network system is addressed. The communication network system consists of a transmitter which sends messages to a receiver. The proposed model considers two possibilities. The first one, that messages are successfully received, while in the second one, during the sending process the transmitter breaks down and as a result the message does not reach the receiver. A communication network system can be considered as a dynamical system whose state evolves in time by the occurrence of events at possibly irregular time intervals, (therefore belong to the class of dynamical systems known as discrete event systems). Place-transitions Petri nets (commonly called Petri nets) are a graphical and mathematical modeling tool that can be applied to the communication network system in order to represent its states evolution. Petri nets are known to be useful for analyzing the systems properties in addition of being a paradigm for describing and studying information processing systems. Timed Petri nets are an extension of Petri nets, where now the timing at which the state changes are taken into consideration. This is of critical importance since it allows considering useful measures of performance as for example: how long does the communication network system spends at a given state etc. For a detailed discussion of Petri net theory see [1] and the references quoted therein. One of the most important performance issues to be considered in a communication network system is its stability. Lyapunov stability theory provides the required tools needed to aboard the stability problem for communication network systems modeled with timed Petri nets whose mathematical model is given in terms of difference equation. By proving practical stability one is allowed to preassigned the bound on the communication network systems dynamics performance. Moreover, employing Lyapunov methods, a sufficient condition for the stabilization problem is also obtained. It is shown that it is possible to restrict the communication network systems state space in such a way that boundedness is guaranteed. However, this restriction results to be vague. This inconvenience is overcome by considering a specific recurrence equation, in the max-plus algebra, which is assigned to the timed Petri net graphical model. The paper is organized as follows. In Section 2, Lyapunov theory for discrete event systems modeled with Petri nets is given. Section 3 presents max-plus algebra. In Section 4, the solution to the stability problem for discrete event systems modeled with timed Petri nets is considered. Finally, in Section 5 the modeling and stability analysis for communication network systems is addressed. Some conclusion remarks are also provided.

2. Lyapunov Stability and Stabilization of Discrete Event Systems Modeled with Petri Nets [2] [3]

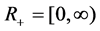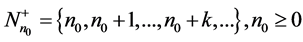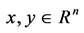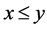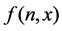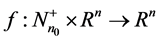NOTATION:, ,. Given, is equivalent to. A function, is called nondecreasing in x if given 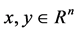such that 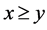and then,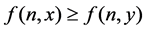. Consider systems of first ordinary difference equations given by

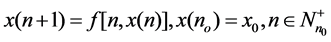(1)

where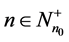, and 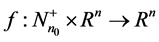is continuous in.

Definition 1. The n vector valued function is said to be a solution of (1) if and for all.

Definition 2. The system (1) is said to be practically stable, if given with, then.

Definition 3. A continuous function is said to belong to class if and it is strictly increasing.

Consider a vector Lyapunov function, and define the variation of v relative to (1) by

(2)

Then, the following result concerns the practical stability of (1).

Theorem 4. Let be a continuous function in x, define the function such that satisfies the estimates

(3)

for, , where is a continuous function in the second argument. Assume that: is nondecreasing in e, are given and finally that is satisfied. Then, the practical stability properties of

(4)

imply the practical stability properties of system (1).

Corollary 5. In Theorem (4): if we get uniform practical stability of (1) which implies structural stability.

Definition 6. A Petri net is a 5-tuple, where: is a finite set of places, is a finite set of transitions, is a set of arcs, is a weight function,: is the initial marking, and.

Definition 7. The clock structure associated with a place is a set of clock sequences

The positive number, associated to, called holding time, represents the time that a token must spend in this place until its outputs enabled transitions fire. We partition P into subsets and, where is the set of places with zero holding time, and is the set of places that have some holding time.

Definition 8. A timed Petri net is a 6-tuple where are as before, and is a clock structure. A timed Petri net is a timed event Petri net when every has one input and one output transition, in which case the associated clock structure set of a place reduces to one element

Notice that if (or) then, this is often represented graphically by, () arcs from p to t (t to p) each with no numeric label.

Let denote the marking (i.e., the number of tokens) at place at time k and let denote the marking (state) of PN at time k. A transition is said to be enabled at time k if for all such that. It is assumed that at each time k there exists at least one transition to fire. If a transition is enabled then, it can fire. If an enabled transition fires at time k then, the next marking for is given by

(5)

Let denote an matrix of integers (the incidence matrix) where with and. Let denote a firing vector where if is fired then, its corresponding firing vector is with the one in the position in the vector and zeros everywhere else. The nonlinear difference matrix equation describing the dynamical behavior represented by a PN is:

(6)

where if at step k, for all then, is enabled and if this fires then, its corresponding firing vector is utilized in the difference equation to generate the next step. Notice that if can be reached from some other marking M and, if we fire some sequence of d transitions with corresponding firing vectors we obtain that

(7)

Let be a metric space where is defined by and consider the matrix difference equation which describes the dynamical behavior of the discrete event system modeled by a PN, see (7).

Proposition 9. Let PN be a Petri net. PN is uniform practical stable if there exists a strictly positive m vector such that

(8)

Moreover, PN is uniform practical asymptotic stable if the following equation holds

(9)

Lemma 10. Let suppose that Proposition (9) holds then,

(10)

Remark 11. Notice that since the state space of a TPN is contained in the state space of the same now not timed PN, stability of PN implies stability of the TPN.

Lyapunov Stabilization

Definition 12. Let PN be a Petri net. PN is said to be stabilizable if there exists a firing transition sequence with transition count vector u such that system (7) remains bounded.

Proposition 13. Let PN be a Petri net. PN is stabilizable if there exists a firing transition sequence with transition count vector u such that the following equation holds

(11)

Remark 14. By fixing a particular u, which satisfies (11), the state space is restricted to those markings that are finite.

3. Max-Plus Algebra [4] [5]

3.1. Basic Definitions

NOTATION:, ,. Let and define the operations and by: and.

Definition 15. The set with the two operations and is called a max-plus algebra and is denoted by

Definition 16. A semiring is a nonempty set R endowed with two operations and two elements and such that: is associative and commutative with zero element is associative, distributes over, and has unit element is absorbing for i.e., , In addition if is commutative then R is called a commutative semiring, and if is such that, then it is called idempotent.

Theorem 17. The max-plus algebra has the algebraic structure of a commutative and idempotent semiring.

3.2. Matrices and Graphs

Let be the set of matrices with coefficients in with the following operations: The sum of matrices, denoted is defined by: for i and The product of matrices, denoted is defined by: for i and. Let denote the matrix with all its elements equal to and denote by the matrix which has its diagonal elements equal to e and all the other elements equal to. Then, the following result can be stated.

Theorem 18. The 5-tuple has the algebraic structure of a noncommutative idempotent semiring.

Definition 19. Let and then the k-th power of A denoted by is defined by:, (k times), where is set equal to E.

Definition 20. A matrix is said to be regular if A contains at least one element distinct from in each row.

Definition 21. Let be a finite and non-empty set and consider. The pair is called a directed graph, where is the set of elements called nodes and is the set of ordered pairs of nodes called arcs. A directed graph is called a weighted graph if a weight is associated with any arc.

Let be any matrix, a graph, called the communication graph of A, can be associated as follows. Define and a pair will be a member of, where denotes the set of arcs of.

Definition 22. A path from node i to node j is a sequence of arcs such that, for and. The path p consists of the nodes with length m denoted by. In the case when the path is said to be a circuit. A circuit is said to be elementary if nodes and are different for. A circuit consisting of one arc is called a self-loop.

Let us denote by the set of all paths from node i to node j of length and for any arc let its weight be given by then the weight of a path denoted by is defined to be the sum of the weights of all the arcs that belong to the path. The average weight of a path p is given by. Given two paths, as for example, and in the concatenation of paths is defined as. The communication graph and powers of matrix A are closely related as it is shown in the next theorem.

Theorem 23. Let, then:, where in the case when is empty i.e., no path of length k from node i to node j exists in.

Definition 24. Let then define the matrix as:. Where the element gives the maximal weight of any path from j to i. If in addition one wants to add the possibility of staying at a node then one must include matrix E in the definition of matrix giving rise to its Kleene star representation defined by:

Lemma 25. Let be such that any circuit in has average circuit weight less than or equal to. Then it holds that:

Definition 26. Let be a graph and, node j is reachable from node i, denoted as, if there exists a path from i to j. A graph G is said to be strongly connected if. A matrix is called irreducible if its communication graph is strongly connected, when this is not the case matrix A is called reducible.

Remark 27. In this paper irreducible matrices are just considered. It is possible to treat the reducible case by transforming it into its normal form and computing its generalized eigenmode see [4].

3.2.1. Spectral Theory and Linear Equations

Definition 28. Let be a matrix. If is a scalar and is a vector that contains at least one finite element such that: then, is called an eigenvalue and v an eigenvector.

Let denote the set of all elementary circuits in and write: for the maximal

average circuit weight. Notice that since is a finite set, the maximum is attained (which is always the case when matrix A is irreducible). In case define.

Definition 29. A circuit is said to be critical if its average weight is maximal. The critical graph of A, denoted by, is the graph consisting of those nodes and arcs that belong to critical circuits in.

Theorem 30. If is irreducible, then there exists one and only one finite eigenvalue (with possible several eigenvectors). This eigenvalue is equal to the maximal average weight of circuits in .

Theorem 31. Let and. If the communication graph has maximal average circuit weight less than or equal to e, then solves the equation. Moreover, if the circuit weights in are negative then, the solution is unique.

3.3. Max-Plus Recurrence Equations for Timed Event Petri Nets

Definition 32. Let for and for;. Then, the recurrence equation: is called an Mth order recurrence equation.

Theorem 33. The Mth order recurrence equation, given by equation, can be transformed into a first order recurrence equation; provided that has circuit weights less than or equal to zero.

With any timed event Petri net, matrices can be defined by setting, where is the largest of the holding times with respect to all places between transitions and with m tokens, for, with M equal to the maximum number of tokens with respect to all places. Let denote the kth time that transition fires, then the vector, called the

state of the system, satisfies the Mth order recurrence equation: Now, assuming that all the hypothesis of theorem (33) are satisfied, and setting, equation can be expressed as:, which is known as the standard autonomous equation.

4. The Solution to the Stability Problem for Discrete Event Dynamical Systems Modeled with Timed Petri Nets

Definition 34. A TPN is said to be stable if all the transitions fire with the same proportion i.e., if there exists such that

(12)

This means that in order to obtain a stable TPN all the transitions have to be fired q times. It will be desirable to be more precise and know exactly how many times. The answer to this question is given next.

Lemma 35. Consider the recurrence relation, arbitrary. A an irreducible matrix and its eigenvalue then,

(13)

Proof. Let v be an eigenvector of A such that then, .

Now starting with an unstable TPN, collecting the results given by: proposition (13), what has just been discussed about recurrence equations for TPN at the end of subsection (3.3) and the previous lemma (35) plus theorem (30), the solution to the problem is obtained.

5. Modeling and Stability Analysis of a Communication Network System

In this section, the modeling and stability analysis for a communication network system is addressed. The communication network system consists of a transmitter which sends messages through a communication channel to a receiver. The proposed model considers two possibilities. The first one, that messages are successfully received, while in the second one, during the sending process the transmitter breaks down and as a result the message does not reach the receiver. Consider a communication network system whose TPN model is depicted in Figure 1.

Where the events (transitions) that drive the system are: q: receivers connect to the communication network, s: messages are sent, b: the transmitter breaks, r: the transmission is restored, d: the message has been successfully received. The places (that represent the states of the queue) are: A: receivers concentrating, P: the receiver is waiting for a message to be sent, B: the message is being received, D: transmitter breaks down, I: the transmitter is idle. The holding times associated to the places A and I are and respectively (with). The incidence matrix that represents the model is

Therefore since there does not exists a strictly positive m vector such that the sufficient condition for stability is not satisfied, (moreover, the () is unbounded since by the repeated firing of q, the marking in P grows indefinitely). However, by taking (but unknown) we get that Therefore, the is stabilizable which implies that the is stable. Now, let us proceed to determine the exact value of k. From the model we obtain that:

and which implies

leading to:

Therefore,. This means that in order for the to be stable and work properly the speed at which the receivers concentrate has to be equal to (the firing speed of transition q) which is attained by taking.

6. Conclusion

This paper studies the modeling and stability problem for communication network systems using timed Petri nets, Lyapunov methods and max-plus algebra. The results obtained are consistent to what was expected.

Cite this paper

Zvi Retchkiman Königsberg, (2015) Modeling and Stability Analysis of a Communication Network System. Journal of Computer and Communications,03,176-183. doi: 10.4236/jcc.2015.311028

References