Received October 2015

ABSTRACT

Network localization is a fundamental problem in wireless sensor networks, mainly in location dependent applications. A common family of solutions to this problem is the range-based network localization. The resulting localization algorithms are noise sensitive and thus lacking in terms of robustness. Our contribution provides an algorithm which is robust to measurement errors. We propose an analytical tool to analyze the effect of range errors in the final location and use a distributed method to solve the noisy range localization problem.

Keywords:

Network Localization, Noisy Range Measurement, Distributed Computation

1. Introduction

Estimating the positions of agents in networked systems is crucial for many applications ranging from robotics, autonomous vehicles navigation and sensor networks. In network localization, the absolute node positions need to be estimated from partial relative measurements between nodes. For range-only localization problem, the inter-agent distance information is given, and we need to estimate the agents’ location. In noiseless case the problem usually has a unique global solution. In practice, the inter-agent distances are often measured with perturbations. Thus, the existence and uniqueness of the global solution are not guaranteed. Indeed, it is well known that in presence of distance noise, a node may have discontinuous deformations (e.g. flip ambiguities and discontinuous flex ambiguities). Then the location estimation error needs to be analyzed. In this paper, we focus on the noisy distance network localization problem.

There are some previous works related with the noisy range network localization. Some authors consider the location error properties with the particular measurement model. [1] derives Cramer-Rao Bound (CRB) error of location for Time-Of-Arrival and Received Signal Strength measurements. [2] derives CRB error from distance and angle measurements model and gives the properties of CRB error with network parameters. Anderson states that when the distance noise is small enough, the noisy minimization problem has a unique solution and the displacements of agent positions have a bound based on the distance noise [3]. Other authors focus on network multi-lateration techniques to search a global solution in noisy range network localization problem. [4] describes a hybrid centralized and distributed algorithm, which provides robust quadrilaterals as subgraph from representative network graph to avoid flip ambiguities. [5] proposes a technique based on Cayley-Menger determinant to formulate the geometric relations among sensors and anchors in sensor networks as quadratic constraints. [6] proposes two computational efficiently algorithms in n-lateration networks to refine the noisy distances based on the Cayley-Menger determinant. [7] proposes a successive refinement method, Semi-Definite Programming (SDP), trying to get a rude solution for the global optimization in the noisy case.

In noisy range-based network localization cases, most of the existing approaches to solve the problem are network multi-lateration based techniques. Typically, successive refinement approaches achieve better statistical performance than multi-lateration approaches in noiseless case. But the existing SDP method is a centralized one. In this paper, we want to investigate the noisy localization performance of a distributed gradient-based algorithm that we propose in [8].

The organization of the paper is as follows. In the Section 2, we formulate the range-based network localization problem in noisy case. In Section 3, we derive the analytical location estimation error characterizations from the Gaussian random distance perturbation model. In Section 4, we will give short overview of the distributed gradient-based localization algorithm. In Section 5, the numerical simulations are performed to prove the robustness of the localization algorithm with the distance noise and accuracies with the network parameters. In Section 6, we summarize the results.

2. Problem Statement

Let 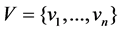be a set of n nodes (representing sensors, agents, robots, vehicles, etc.), and let 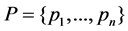denote a corresponding set of positions on the Cartesian plane, where 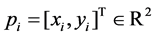are the coordinates of

the i-th node. We shall call P a configuration of nodes. Suppose that some pair of nodes, say nodes (i, j), have the possibility of measuring the relative distance between them:

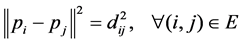. (1)

We denote with E the set of unordered node pairs (i, j) such that a distance measurement exists between i and j. Our objective is to determine a node configuration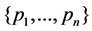, that minimizes a Least-Squares of fit criterion

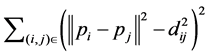(2)

When the global minimum of 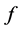is zero, we say that exact matching is achieved, that means a configuration 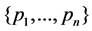is found that exactly matches the given distance measurements. Otherwise, no geometric node configuration can exactly match the given range data, and we say that approximate matching is achieved by the optimal configuration. Actual recovery of the absolute geometric node positions from distance measurements is only possible if the node configuration is generically globally rigid (ggr), [9]. In this case, the objective function in (2) has a unique global minimum, if the positions of at least three nodes are known and fixed in advance (anchor nodes, or beacons).

2.1. Problem Setup

In noiseless case, after using anchor and distance information, network localization can be formulated.

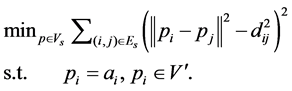(3)

where, 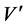is the vertex set of anchors, (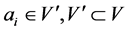).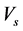is the set of the unknown sensors,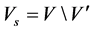. 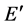is the set of edges between anchors. 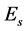is the set of edges between anchors and unknown sensors,.

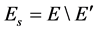In practice, the distance measurements are usually noisy. We assume the distance measurement model, Where, is the distance measurement, is the true distance and is the measurement noise in the square of the distance.

2.2. Linear Algebra Property of the ggr Formation

Let, denote the vector of node positions. The cost function (2) is rewritten as

(4)

The gradient is a row vectors,

Then the rigidity matrix R of the configuration can be written:

(5)

Let denote the cardinality of set, and the k-th edge denote edge between nodes i and j, i.e.,. Notice that in the case when anchor nodes are present, by eliminating the columns of R corresponding to anchors and each row of R corresponding to the edges between the anchors pairs, we have the reduced rigidity matrix as the submatrix obtained from R.

Based on lemma 1 [10], there is, which means the number of Equation (1) is larger than the number of the unknown variables, i.e. with the assumption of ggr formation, the equation set (1) constitutes an overdetermined system of simultaneous equations and then the solution is unique. In the noiseless case, the global optimum can be found with the ggr formation assumption. In the noisy case the unique global will not exist, except that the distance bound is typically small [3].

3. Location Estimation Error Properties in Noisy Range Network Localization

We need to know what is the effect of distance errors on the error of network localization. In this section, we propose two analytical ways to derive the error propagation. We assume the distance perturbation, is independent Gaussian random noise,. We derive the Cramer-Rao Bound (CRB) of position error with independent Gaussian random distance error model. CRB is an independent-algorithm way to express a lower bound on the covariance of unbiased estimator for deterministic parameters. This benchmark implies that if the bound is nearly achieved, then there is no need to improve the accuracy of the algorithm.

For the k-th edge in the global rigid graph, location estimation function becomes:. Let. We stack all the equations and have:

where,

Under Gaussian independent random distance assumption, the measurement pdf of the distance is:

Since we assume that the distance measurements are uncorrelated, the covariance matrix is a diagonal matrix and the nonzero element. Then the measurement pdf is the vector Gaussian pdf:

(6)

From the measurement pdf (6), we find the Fisher information matrix:

(7)

where,

According to the definition of the rigidity matrix R, by omitting the anchor information we have. We get the new form for the Fisher information matrix as follows:

So the Cramer-Rao Bound matrix is:

(8)

The position estimate error covariance matrix defined as, and it is lower bounded by the Cramer-Rao Bound:.

Distributed Gradient-Based Localization Algorithm

In the previous section, we derived the analytical bounds for the localization error. We will use these bounds for analyzing the performance of the Distributed Gradient-based Method (DGM). This algorithm and its equivalent centralized version (GM) were previously presented in [8] under noise-free distance measurements.

Distributed Gradient-based Method Algorithm: Let t denote the number of consensus iterations, denote the number of gradient update iterations, denote the configuration by algorithm in update iteration. is the neighbors communicated with node i. W is a symmetric, non-negative with strictly positive diagonal entries, doubly stochastic matrix, compatible with graph G.

Input:, Maximum number of consensus iterations;, Maximum number of gradient updates;, Maximum number of warm-up iterations;, Absolute update tolerance.

Initialization and Warm-up: Let and set the position estimates, for, to be the given initial guess for optimization. Mark all nodes as “active”. Repeat while: Fix (a small number and equal for all nodes); Update all node position estimates according to,

;

Loop until: (Consensus iterations) Repeat while: Initialize and as:

,;

Update and according to:

, (9)

(Gradient update) At each active node: Compute according to

Update position estimate according to (9); If, then mark node as “inactive”;

Let. If, or all nodes are inactive, then exit.

End loop.

4. Numerical Experiments

In this section, we analyze the performance of our localization algorithm using the error characterization given the noisy range measurements. We compare the analytical errors with the estimation errors computed by the particular algorithm. We display the root-mean-square (RMS) error associated to the CRB matrix, given by

(10)

where are non-anchor node positions to be determined. For our localization algorithm under noisy measurements, we display algorithm estimate error defined by

(11)

where are the estimated positions for the non-anchor nodes, and is the true configuration. In addition, the behavior of the algorithm with parameters such as the number of nodes, the number of anchor-nodes and the noise level are also discussed.

4.1. Network Generation

We have performed several simulations using range limited graphs, which are generically global rigid and have at least three non collinear anchor nodes. Therefore, the global solution of the localization problem is unique. We use random geometric graphs, in which nodes are deployed at random in the square plane, and an edge exists between a pair of nodes if and only if their geometrical distance is smaller than sensing radius, r. It has been proved in [9] that if, the graphs produced by the previous technique are ggr with high probability. In the following experiments, the sensing range is. The nodes are distributed in a square with nodes including 3 anchors.

4.2. Location Error Behavior as Range Error

Firstly, we investigate the error characterization with different standard deviations of the distance errors (Figure 1(a)). We generate Gaussian noises with zero mean:. The tested noise levels are appropriate for modeling state-of-the-art real measurement techniques [2]. We generate several random geometry graphs with a fixed network size and with anchors. For each, we run 100 Monte-Carlo simulations. The initial guess of configuration is simulated by corrupting the true node positions with Gaussian noises with zero mean and standard deviation.

We compare the performance of Distributed Gradient based Method (DGM) to the Semi-Definite Programming (SDP) relaxation-based method, which is a classical successive refinement approach used in range localization scenarios. Figure 1(a) shows the localization errors of algorithms DGM and SDP based on Equation (11). When there is no distance error () both algorithms converge to the ground truth. In presence of noises, the results for the DGM are better than the ones associated to the SDP method, for all noise levels. Thus, the distributed gradient-based algorithm is more robust to the range error than the SDP. It can be seen that, as the noise levels in the measurements (x-axis) increases, the error estimates increase as well, with an approximately linear trend. Figure 1(b) shows that the distributed version of our algorithm DGM behaves similarly to the centralized counterpart gradient based method (GM) in the noisy range network localization problem. The localization errors of the two gradient-based modes converge to the same value which is close to the Cramer-Rao Bound (CRB) error as the update iterations increase.

4.3. Location Error Behavior as Range Error

We investigate how the localization error is affected by the number of nodes in a network. We fix the number of anchors, and simulate scenarios with different number of nodes. We test three noise levels. Figure 2 shows that as the number of nodes increases, the location estimates become more accurate and have lower errors. As long as the network gets almost complete communications the improvement in the estimates accuracy is low. In all cases, the position estimation errors obtained with distributed gradient-based method are almost indistinguishable from the Cramer-Rao bound errors.

5. Conclusion

This paper focused on the analysis of distance noise effects for range-based network localization problems. A analytical tool, CRB errors, to derive the location error propagation have been discussed. A Distributed Gradient-based Method (DGM) is used to solve the noisy range localization problem. We have shown that our algorithm is robust to a wide range of noise levels in the measurements. This is not the case for several noise-free localization algorithms; particularly we have shown that Semi-Definite Programming method (SDP) is sensitive to noises.

Cite this paper

Mingzhu Wei,Ryad Chellali,Yang Yi,Ting Wang,Wen Qin, (2015) Location Characterization in Noisy Range Network Localization. Journal of Computer and Communications,03,126-132. doi: 10.4236/jcc.2015.311020

References