 Intelligent Control and Automation, 2015, 6, 271-288 Published Online November 2015 in SciRes. http://www.scirp.org/journal/ica http://dx.doi.org/10.4236/ica.2015.64025 How to cite this paper: Saidani, S. and Ghariani, M. (2015) Static Simulation of a 12/8 Switched Reluctance Machine (Ap- plication: Starter-Generator). Intelligent Control and Automation, 6, 271-288. http://dx.doi.org/10.4236/ica.2015.64025 Static Simulation of a 12/8 Switched Reluctance Machine (Application: Starter-Generator) Sihem Saidani, Moez Ghariani Laboratory of Electronics and Information Technology (LETI), Electric Vehicle and Power Electronics Group (VEEP), National School of Engineers of Sfax, University of Sfax, Sfax, Tunisia Received 4 May 2015; accepted 17 November 2015; published 20 November 2015 Copyright © 2015 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract Because its high efficiency, its simple stator and rotor structures, the low cost and high reliability, speed operation combined with robust and low cost construction, the switched reluctance machines have represented. In recent years, an interesting alternative to other machine types has been chosen for traction applications especially starter-generator. Their rotors do not generate sig- nificant heat, resulting in easy cooling. Their unidirectional flux and current may generate lower core losses and require a simple converter design. Moreover, the switched reluctance machines are known for their high reliability and capability of operating in four quadrants for a variable speed drive. Despite thos e merits, switched reluctance machine has not been extensively used until re- cently because of its problems of torque ripples and noise. Additionally, researchers have faced many difficulties to build a SRM model because it is inherently multivariable. It has strong coupling and especially a high nonlinearity. In this paper, we deal with many modeling methods. Numerical, analytical and intelligent approaches are studied. The important aim in this research is to use static results from FEMM simulation as flux-linkage, co-energy, static torque to form a dynamic model of a switched reluctance machine used next as a starter-generator of a hybrid vehicle. Keywords Hybrid Vehicle, Switched Reluctance Machine, Finite Element Analysis, Look up Table, FEMM, MATLAB -Simu li nk 1. Introduction The d esign and the materials used in production pre ciseness plus the time are coming the major factors taken in  S. Saidani, M. Ghariani motor manufacturing. As a matter of fact, interior permanent magnet machines (IPM) seem to be the best can- didate in hybrid vehicles. However, and due to many problems as the earth magnet materials and increasing prices especially the Dysprosium and Neodymium, the auto makers have looked for new alternatives. Thus, the switched reluctance machines (SRM), having a near performances especially high efficiency, is one of the best replacing candidates. This machine is characterized by a high starting torque and efficiency similar to a high-ef- ficiency IM. As its rotor is so simple, it is usually made by steel laminations in order to minimize the cor e losses without any windings or magnets. The SRM is the machine suited for harsh environments. Thus, the torque rip- ple, vibration, and acoustic noise are the most disadvantages of the SRM. The acoustic noise in SRMs is caused by the radial forces that inversely increase with the air gap and especially when the force frequency is near the stator resonant frequency. Many issues aimed to analyze SRM design and predict its performance in order to at- tend the best performances. Obviously, the static characteristics exactly the flux linkage and the torque versus current profiles play an important role in the prediction of the dynamic behavior of switched reluctance motors and then as their func- tions as starters and genera tors in micro-hybrid vehicle . 2. SRM as a Starter Alternator The electric motor of a starter alterna tor system must have a high starting torque for initial acceleratio n and then and high efficiency to extend the battery range and a wide operating speed range as generator. Besides, the SRM offers a wide choice of pole configurations and phase number. Consequently, a lower number of phases can re- duce the converter cost, but it increases the torque ripple for example as three phases 12/8 poles is better than 3 phases 6/4 poles as we will explain later. Different design found with the technology of the start-stop system has been described in [1] are used as a European markets for an example: Bosh, Valeo, INA (Schaeffler Techn olo- gies), Benso represented in different configurations as: • Belt Driven starter generator. • Enhanced starter. • Direct Starter. • Integrated Starter Generator. 3. Modeling Methods of Switched Reluctance Machine Due to saturation effects in the SRM, establishing the accurate nonlinear mapping relationship of the flux lin- kage with respect to phase current and rotor position is the basis of performance calculation. For many years, different modeling methods have been proposed by worldwide researchers such as O. Ichinokura in 2003, S. Song also Z. Lin. Generally, all these methodologies can be divided into three categories: The numerical, the analytical and the intelligent methods. 3.1. Intelligent Method There are many intelligent methods that can build a model of SRM, such as artificial neural network (ANN), fuzzy inference system (FIS), B-spline neural network (BSNN) and others. Based on optimization algorithm of Levenberg-Marquardt (LM) in 2005-2006 the BPNN seemed to execute with perfect result the nonlinear rela- tionship between the flux linkage and the electromagnetic torque. This approach had given through its results a strong robustness and a great ability especially for a non user or professional to model easily the SRM. Many researchers had been investigated in the dynamic behavior of (SRM) [2] by monitoring its dynamic response (torque and speed), and then they worked n minimizing the torque ripples and building different types of sensors in order to reduce the cost first and second to improve the SRM and reliability and performance. Many re- searches have proved the powerful problem-solving methodology of the Fuzzy logic with the control and the information process. Moreover the Fuzzy logic control (FLZ) seemed to be extremely a simple way to find pr e- cise solutions. 3.2. Analytical Methods In the analytical approach, the nonlinear relationships of the phase inductance and torque to phase current and rotor posi tion can be re p re s ented using different analytical expressions: [3] 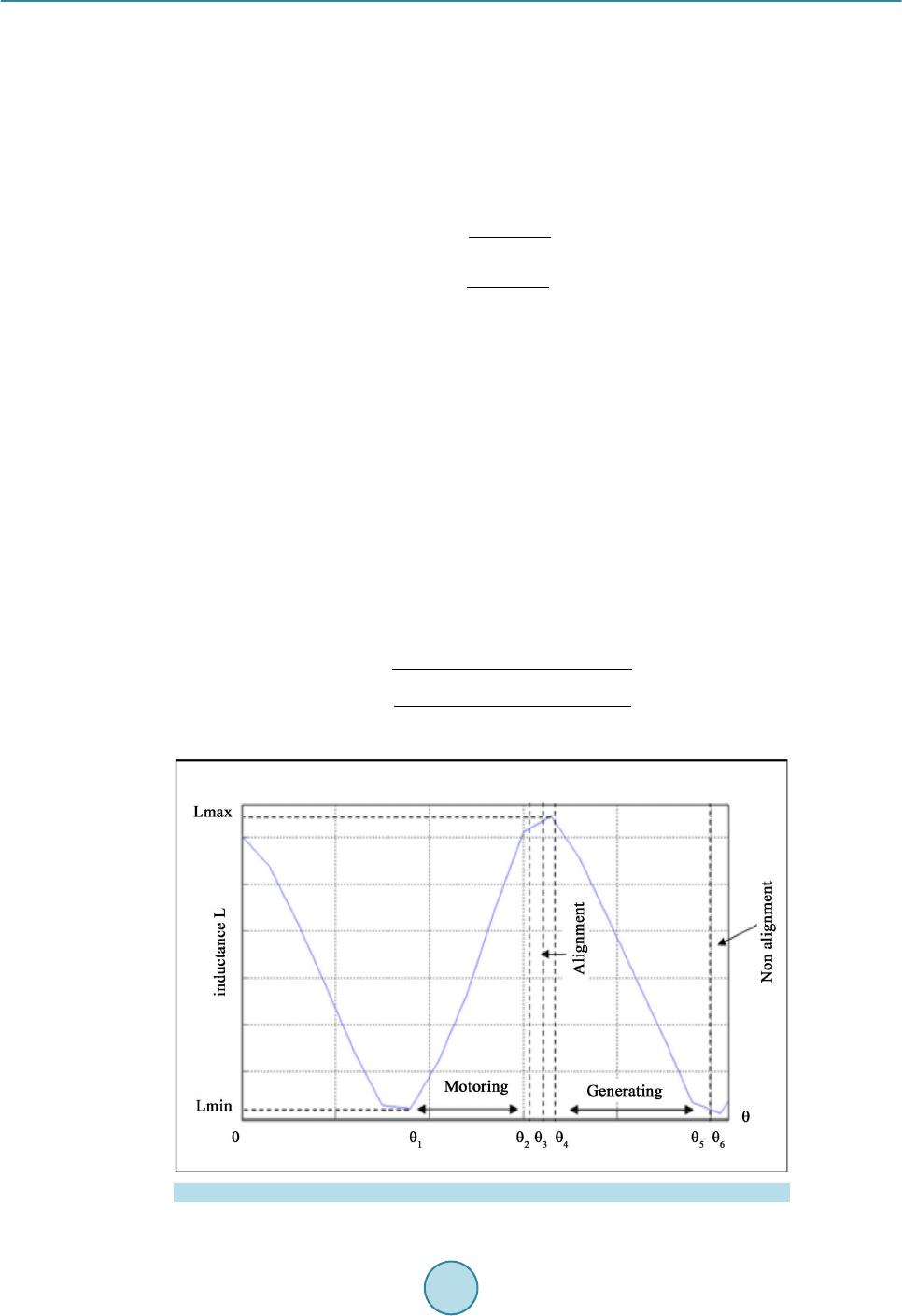 S. Saidani, M. Ghariani ()( )( )() 1 0 , cos n r kk L iLiLinN θθ = =+ ∑ (1) where is the inductance of an independent phase, L0 and Lk are a constant coefficients, Nr is the number of rotor’s pole and θ is the rotor position and n is the maximum harmonic order. Generally, the inductance val- ues at two different rotor positions Lmin and Lmax. For the first harmonic (n = 1), we can write: ()( )( )() 01 , cos r L iLiLiN θθ = + (2) where: ( ) ( ) min max 0 min max 1 (3) 2 (4) 2 LL Li LL Li + = − = The current pulses are applied on precise rotor position and the motor creates torque in the direction of in- creasing inductance. In Figure 1, we rep resen t: • The torque is posit i ve when dL/dθ > 0 from θ1 to θ2, and the SRM so it is the motoring mode. • (see Figure 13). • The torque is negative when dL/dθ < 0 from θ4 to θ5, and the SRM so it is the generating mode. The inductances Lmin and Lmax can be seen as a constant. Thus, these inductances can be calculated analytical- ly by polynomial fitting using MATLAB for example, as Lmax and Lmin given by this re lation: (5) where the ak are a constant coefficients, Using the relation: (6) The curve of flux linkage can be deduced and so the static torque deduced in (8): ( ) ( ) ( ) min 0 min 0 ,2 cos 2 k k k k kr n k n L ai Li Lai N θθ = = + =+− ∑ ∑ (7) Figure 1. Inductance vs. rotor position angle.  S. Saidani, M. Ghariani ( ) 2min 0 2sin 42 k k rr k n a N TiLi N k θ = =−− + ∑ (8) 3.3. Numerical Method Lately and due to the development of power electronics, it becomes possible to control the SRM. There for, even with acoustic noise, torque ripple, special converter technology control etc., many researchers have developed new methods of design throw geometric modeling, finite an alysis (FEA, BEA..) in order to optimize its perfor- mance and make the more and more suitable for the drive -train application especially in the hybrid vehicle. 1) FEA Recently, the finite element analysis has become useful in the machine design stage. Where, the flux distri- bution may be computed in all the regions of the machine, with no geometric limitations or bound ary cond itions of several material properties. Thus, much useful detailed information has facilitated the range of analysis like noise and vibration issues. 2) The BEA The nonlinear boundary element method is also another alternative way to modulate a machine design. Its principles and equation formulations have been well documented in [2]. The BEA, easier of processing so suita- ble for both design optimization and dynamic simulation, allows a medium movement without meshing bounda- ries and a very smooth integral operations without even the unpredictable differentiation used in FEA [3] [4]. 3) Finite Element Method (FEM) The finite element method can solve the governing differential equations in order to obtain the magnetic po- tentials that are minimizing the parameters to have optimized energy. Many tools of finite elements have been developed last years in order to compute the accurate properties and magnetic characteristics of machine without constructing a real prototype. FEMM is a program that can solve electromagnetic problems on 2D (two-dime n - sional planar). Thus, we can resolve linear and nonlinear magneto static, harmonic magnetic, linear electrostatic and steady state heat problems. The determination of magnetic characteristics facilitates the optimization and control of switched reluctance machine. In particular, the switched reluctance machine phase magnetization characteristics vary hardly as a function of both excitation current and rotor position. Thus, numerical methods have used in order to calculate the magnetic field and to predict the magnetization characteristics. 4. Finite Element of Switched Reluctance Machine The Finite Element Method Magnetics (FEMM) as a numerical technique is used to find approximate solutions of partial differen tial and integral equations. Thus, the solution is approached basically either on eliminating the differential equation completely or rendering the partial differential equation (PDE) into an approximating sys- tem of ordinary differential equations. Then, these ODE are numerically integrated using standard techniques as Runge-Kutta, Euler’s method etc. For example, FEMM version 4.2, used in our work, is using the finite element method. The (FEM) takes into account the property of non-linear used magnetic plus the SRM geometry. The solu- tions of magnetic field distributions allow the torque, flux and flux linkage, losses, energy and co-energy, and in- ductance to be evaluated. Inductance is normally defined using flux linkage (A), or stored magnetic energy (W). Using FEMM, we can generate several characteristics for example the inductance variation the magnetic field energy, Maxwell’s static and instantaneous [5] torque profiles a nd output power) have been obta ined by integral Equation 9 and Equation 10) as examples 4.1. Torque Using the Maxwell Stress Tensor (TST) the force applied to one part of the magnetic circuit and that can be ob- tained by int egrati ng the next equat i o n: ( ) 2 00 11 d 2 TS S TL rBnBBnS µµ = ×⋅− ∫ (9)  S. Saidani, M. Ghariani where: TTS is the static torque, L is the length, B is the induction vector in the elements and r is the lever arm. 4.2. The Magnetic Energy Noted in FEMM (W) as the magnetic field in the specified region and used as an alternate method of getting in- ductance for linear problems (at least not heavily saturated). In case of nonlinear materials, the energy is com- puted wit h Equation (10): (10) where: B is the magnitude of flux density (Tesla), H (A/m) is the magnitude of field intensity and V is the vo- lume of the region obtained from int e gra tion over the 2D region. 4.3. The Flux Linkage In nonlinear characteristics of the SRM, the value of flux and torque depends on with the rotor position and phase current [5] [6]. Therefore, the values of flux and torque must be known for better control of the motor. Thus, the flux or and torque curves can either be obtained using numerical experimentally or computation or by the Finite Element Analysis (FEA). As the matter of fact, the vector po tential A witch determines the magnetic field inside the motor through the next expression called Poisson’s equation: AA J xxyy γγ ∂∂ ∂∂ +=− ∂∂∂∂ (11) where the magnetic reluctivity and J is the current density vector. Using the 2D static analysis of FEMM, we can have when one phase is excited the aligned and unaligned inductance with a stator rotor poles position be- tween 0˚ and 22.5˚ and it occurs at every 22.5˚ interval. For the machine J, at a fixed rotor position, we can cal- culate the co-energy, the static torque and the flux linkage by exciting separately one phase through injecting different values of winding current. 4.4. The Co-Energy The switched reluctance machine is characterized with independent phases. Thus, to obtain th e torque T we can also calculate the energy called also work given in the next Equation (12) (Figure 2): constant 1 0 (12) (13d ) i i W T Wi θ = ′ ∂ = ∂ ′= Ψ ∫ Figure 2. Magnetization curve.  S. Saidani, M. Ghariani The co-energy can also be used to calculate the inductance phase through the Equati o n (14): (14) Regarding to our machine and before getting the static characteristics and next dynamic we need to fulfill such important steps: • Build the model of the motor according to its physical dimension and material. • Build the model of the power converter according to its topology. • Set the terminal and the boundary cond itions. • Add drivi n g s o ur c e s. • Generate the finite element mesh. For our example, Figure 3 shows a 12/8 model of a switched reluctance machine build using FEMM. Evidently, the nonlinearity of switched machine makes very difficult the modeling of the flux linkage or the inductance. Many researchers as have been made to resolve the problem of their calculation from varying the rotor position and the phase. The first way to plot the phase flux linkage is the variations of rotor position and phase current. The second way, at different phase currents we plot the phase inductance variation in functio n of rotor positi on. All thes e stat ic chara cteri stic s are hi ghly nonli near. Figure 4 shows differen t m odeli ng te chniques of switched reluctance machine. 5. Influence of Geometry on Static Behavior The choice of machine’s dimensions is considered essential to provide optimum performance of machine. There are four major factors: • The air-gap length. • The ratio of rotor diameter to machine outside diameter. • The toot h wi dth. • The core back depth cover explanation of choosing the above aspects are explained below. 5.1. Air-Gap Length In order to have the maximum torque, the air-gap length has to be made the smallest possible typically equal to 0.25 mm (in our case 0.32 mm). It is important element because it will fix the area of the co-energy curve W’ (θ, i) witch as large as possible consequently the values of aligned inductance became so high. Figure 3. Triangular meshing of 12/8 SRM using FEMM (35,294 nodes, 70,361 elements). 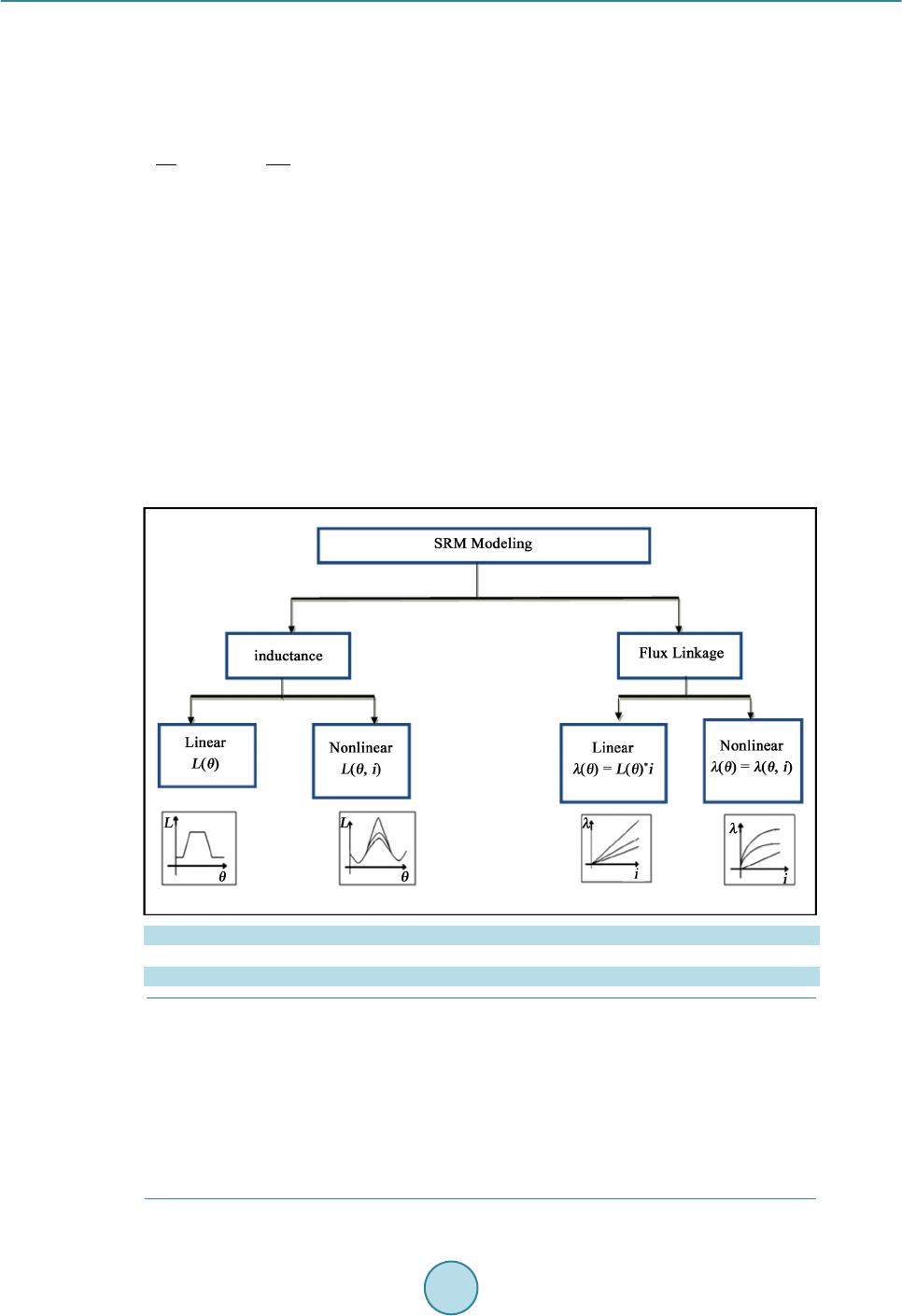 S. Saidani, M. Ghariani 5.2. Ratio of Rotor Diameter to Outside Diameter The ratio of 0.5 to 0.6 is usually used for most machines. The factor of 1/2 comes from the fact that the stator phase sees two identical air gaps in series. The factors k1 and k2 respectively the ratio of rotor interpolar arc to stator pole arc and ratio of rotor pole length to rotor interpolar arc length. A study had been explained carefully to represent the relation between th is ra tio and the unaligned inductance (see Table 1): where: and (see F igure 5). 5.3. Tooth Width Different studies have been made as using diverse stator and rotor teeth w idths were used to compar e the torque ripples. The stator teeth have to be designed to satisfy two conditions: • The narrow teeth could cause saturation and then the maximum flux which limits the SRM performances. • The wide teeth may cause insufficient room for the winding. Therefore, an equal approximately widths be- tween the stator teeth and slots. Then, usua lly in order to estimate tooth width is as a ratio of about 0.3 to 0.5 can be fixed. 5.4. Core Back Depth It is usually fixed as at lea st 0.6 times the width of the s tator teeth. Despite, the core back is occasionally can be made thicker than 0.6 to increase mechanical stiffness and consequently may reduce mechanical noise. Figure 4. Classification of linear switched reluctance machine modeling. Table 1. The unaligned inductance in function of ratio k1/k2. k2/k1 1.05 1.20 1.5 2 2.5 0.125 17.09 12.98 10.22 8.14 7 0.1875 14.48 10.4 7.99 6.25 5.44 0.25 13.22 9.27 6.63 5.42 4.68 0.375 12.33 8.3 6.03 4.65 4.01 0.5 11.86 7.91 5.69 4.36 3.75 0.75 11.56 7.7 5.48 4.18 3.6 1 11.54 7.62 5.43 4.14 3.75  S. Saidani, M. Ghariani 5.5. Other Factors 1) Effect of soft magnetic materials on losses and torque ripple There are several factors either than geometric ones especially the material made of stator. As the matter of fact, the influence of d iff erent s oft magnetic materials (SMC) w ith non-oriented grain also on the core losses and efficiency of a 6/4 SRM has been treated by H. Toda and K. Senda [7]. Besides, the impact of grain oriented (GO) and non-oriented (NO) steel on the electromagnetic characteristics of a 12/8 switched reluctance machine has been analyzed by Y. Sugawara and K. Akatsu. K. Vijayakumar, R. Karthikeyan and R. Arumugam have analyzed the influence of composite materials on the characteristics of electromagnetic torque, the average tor- que and torque ripple. Additionally, these researchers have studied the contribution of composite materials in high speed applications (relatively high frequency is considered), and made a comparison with the M19 material. To improve the performance of a 6/4 SRM, A. Chiba and H. Hayashi used amorphous materials. It’s well acknowledged that one of SRM’s inherent problems in is the torque ripple due to switched nature of the torque production. The Equation (15) explain how to determined torque ripple. The torque ripple (Tripp) represents the distance between the peak value and the common point of overlap in the static torque angle cha- racteristics of two consecutive excited SRM phases (see Figure 6). Thus, we call the maximum value, in next Figure 7, the static torque “peak static torque” as a Tmax and the minimum of the intersec t ion point Tint: Figure 5. A plane projection of stator and rotor. Figure 6. Static torque vs. a rotor position curves of soft materials. 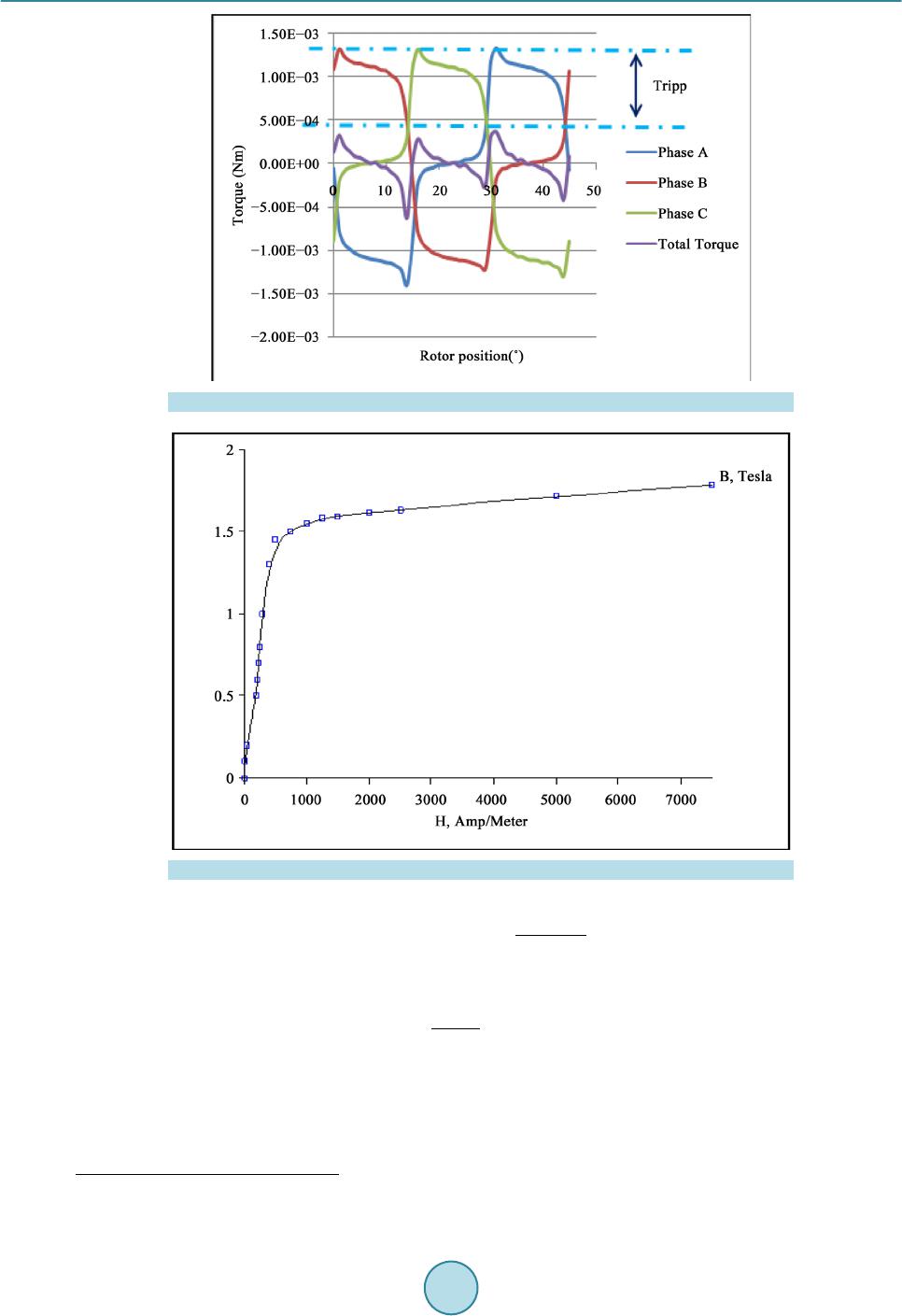 S. Saidani, M. Ghariani Figure 7. Torque ripple for 2 A phase current. Figure 8. Magnetization curve of M800-50 (FeSi 3.5%). max int max %Torque RippleTT T − = (15) The choice of magnetic material in function of the average torque given by the Equat i on (16): ( ) 2π r ava u qN T WW × = ×− (16) where, is th e differ ence of co-energies at aligned and unaligned positions, Nr is the number of rotor poles and q number of machine’s phase. In our case of study we h ave chosen the M80 0-50 (F eSi 3.5%) with a static torque less than 150 nm as shown in Figure 8: 2) Impact of winding configuration Additionally to the effect of soft magnetic materials on SRM configuration, different researches have been 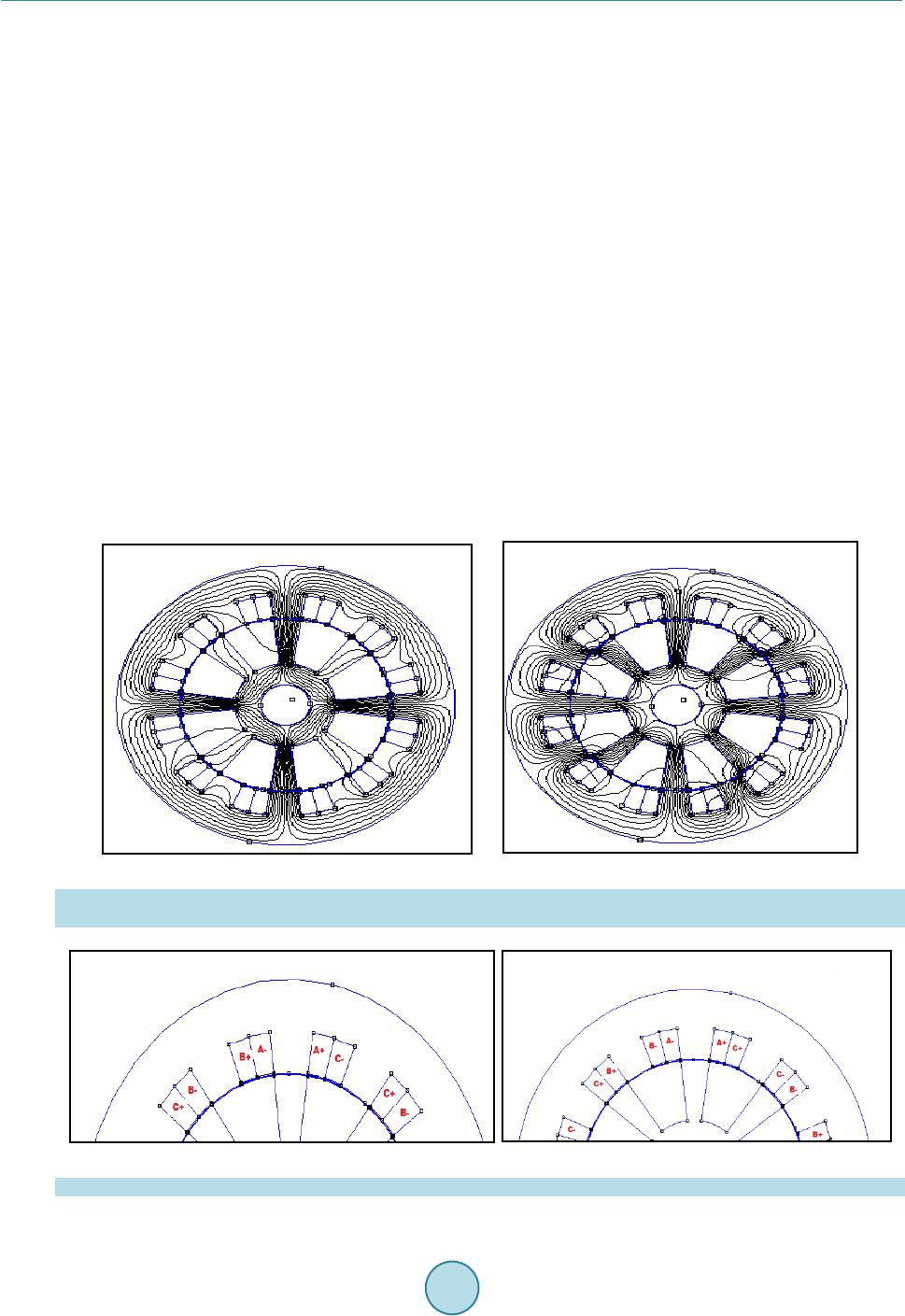 S. Saidani, M. Ghariani developed to improve the impact of winding configuration on the switched reluc tance per for mances . Recen tly, new winding configurations have b een used in the coupling between phases to produce h igher torque density for 3-phase SRMs are studied. Barrie C. Mecrow has presented a n ew winding configuration that called Fully Pitched Winding SRMs witch can produce high density output torque. In order to keep their high output tor- que density and overcome their disadvantages as its longer end-winding and high copper losses performance [8], a new current distribution has been developed with short pitched windings like conventional SRMs. Called Mutually Coupled Switched Reluctance Motors (MCSRMs). Thus, the current distributions of 3 phases is A+_A-_B-_B+_C+_C-_A- _A+_B+_B-_C-_C+ in Figure 9 as a mutually coupled SRMs, and A+_A-_B+_B-_C+_C-_A+_A-_B+_B-_C+_C- in Figure 10 as a MCSRMs. 6. Static Design of 12/8 Switched Reluctance Machine 6.1. Finite Element Analysis of 12/8 SRM The SRM is symmetric so only one phase is modeled. In our studies we have used for torque, flux linkage and inductance the phase A to be excited and to inform out the characteristics obtained. Using the finite elements method through FEMM package according to the steps schematized demands the respect of (see Figure 11). The coupled simula tion program connectin g FEMM and MATLAB softwar e [9], as shown in flowchart of Fig- ure 12: 6.2. Results The SRM used for simulation is a 12/8, 3-phase-machine, the parameters of the machine are given in Appendix A. The finite element model was realized with the FEMM software (see Appendix B). (a) (b) Figure 9. Flux distribution with the phase B excited in constant current (a) conventional SRM, (b) mutually coupled SRM (MCSRM). (a) (b) Figure 10. Winding configurations of SRM 12/8, (a) MCSRM; (b) conventional. 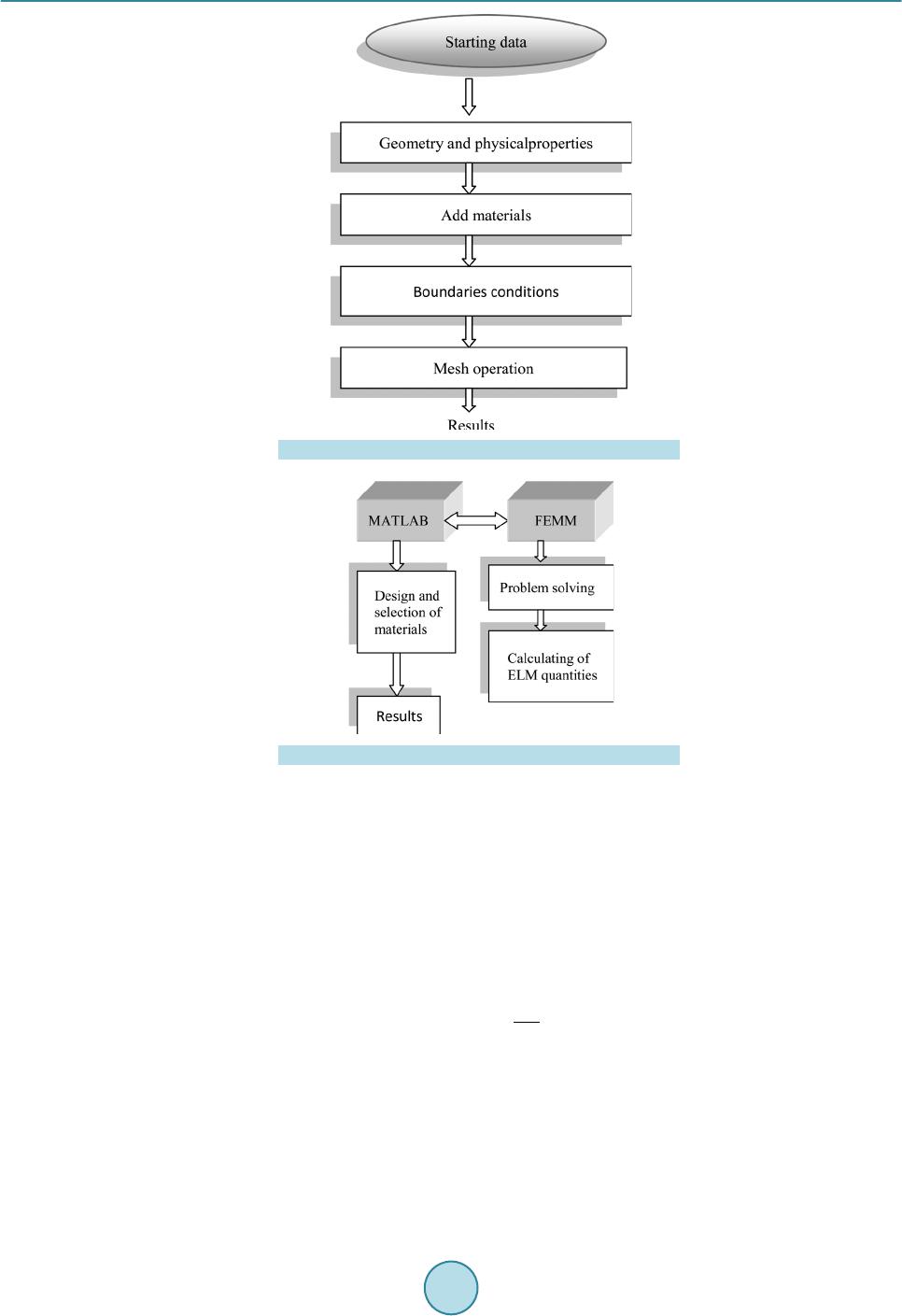 S. Saidani, M. Ghariani Figure 11. A flowchart of FEMM simulation. Figure 12. A flowchart of FEMM-MATLAB coupling. Matlab/Simulink package is the software used in the simulation through the look up table of the torque T(θ, i) in Figure 13 is and the self inductance L(θ, i) of one phase in Figure 14. Thus, and as explained in, the look up table from Simulink library is represented as: • The displacement angles are considered as a row parameters (horizontal parameters), that varied between (0˚ to 47˚). • The current is considered as column parameters (vertical parameters), which is varied between (2 to 30 A). The look-up table described previously in Figure 15 and Figure 16 can be used to determinate the speed in function of time and the rotor position. The calculation of moment of inertia is essential then to calculate the torque using the relation: (17) where: the load torque :the torque :the electromagnetic torque :the roto eed : r sp l e T T T ω  S. Saidani, M. Ghariani Whereas the moment of inertia J can be calculated as explained in: (18) where: D1 and D2 are respectively the external and the internal diameter of the machine and m is the rotor’s weight. This relationship is resolved using the previous LUT in next Figure 17. Figure 13. Static torque for different currents. Figure 14. Self inductance for different rotor position (θ˚).  S. Saidani, M. Ghariani Figure 15. The look up table of the static torque. Figure 16. The look-up table of self-inductance. Figure 17. Speed calculation. Figure18 next represents the scope 3 and 4 where the rotor position (θ) and the speed in function of time :  S. Saidani, M. Ghariani The torque is obtained from the derivate of co-energy. Thus with a simple integration of the look-up table of T(θ, i) as in [2]. We can simply calculate the co-energy using the model in Figure 19 and the result of scope “COENERGY” is presented next in Figure 20: (19) Figure 18. Speed (ω) versus time, (b) angle θ versus time. Figure 19. Calcula ti on model using MATLAB/Simulink to determine co-en erg y from torque. Figure 20. The co energy in function of rotor position (θ) of 12/8 SRM obtained from torque.  S. Saidani, M. Ghariani The flux in the air gap of the machine can be also calculated using the look-up table described in Figure 15 and Figure 16. Using the expression of flux linkage (see Figure 21) relation: (19) Thus, in Figure 22 we deal with the MATLAB/Simulink model us ed in calculation and in Fig ure 22. The re- sult of the simulation: the flux for different current in function of rotor position: Figure 21. Flux linkage in 3 -D. Figure 22. A one -phase inductance calculation.  S. Saidani, M. Ghariani The use of constant current in our simulation was a way to explain simply how to obtain the electromagnetic characteristics in gen eral case. Although in our applicatio n we will us e a 3 phase system of current or voltage to predict the dynamic behavior of the switched reluctance machine in generator and starter mode. Next, through an exciting of the th ree phases with a 3-system of current (see Figure 23) we recuperate the total to rque in Fig- ure 24 which represent the sum of every phase torque excited separately, the flux linkage and the current with a maximum current equal to 300 A in Figure 25. 7. Conclusions It is essential to have a suitable accurate model of the SRM that describes its sta tic characteristics. In literature, several different methods of modeling the static are developed. All these models consider the variation of eith er the phase flux linkage or the phase inductance with rotor position accounting for magnetic saturation. The process of predicting static or even dynamic behavior of a machine needs first a structured methodology that be- gins with fixing the machine parameters through looking for the factors of impact (geometry, materials). Besides, the difficulty of studying a SRM is its highly nonlinear character istics, which must be considered into modeling. However, to obtain a high quality control in either torque or speed control applications, it is necessary to have an accurate model of the machine that describes the static characteristics. Figure 23. A 3-alimentation of the 12/8 SRM. Figure 24. The total torque.  S. Saidani, M. Ghariani Figure 25. The flux of the tree phases. Thus, in this paper, three principle approaches of modeling have been developed namely numerical, analytical and intelligent methods. The numerical one which has been chosen is developed in this paper. The FEMM, coupled to MATLAB for the conception, is a software used to draw a 2Da 12/8 3-phase SRM. The simulation for different rotor positions makes us prepare the flux-linkage curve and then is used to extract the other perfor- mance (static torque, inductance, co-energ y). Then, MATLAB/Simulink is used as a package s oftw are to ob tain the look-up table developed in form of block in Simulink models to calculate different SRM parameters as co- energy, inductance. The modeling technique LUT is a very simple and rapid approach in implementation and structure and establishes an excellent link between finite element method (represented here in FEMM) and dy- namic simulation (with Simulink) . The dynamic model of one phase and typically the other stator phases can be prepared easily using static cha- racteristics and enable us in the next work to develop a control strategy in a Simulink/MATLAB of the three phases of a SRM and then to optimize its characteristics in mode of the alternator and generator in order to avoid the acoustic noise produced by stator vibrations in hybrid vehicle operating mode. References [1] Anderman, M. (2013) Assessing t he Future of Hybrid and Electric Vehicles: Based on Private Onsite Interviews with Leading Technologists and Executives. The xEV Industry Insider Report. [2] Nagrial, M., Rizk, J. and Aljaism, W. (2010) Dynamic Simulation of Switched Reluctance Motor Using Matlab and Fuzzy Logic. Proceedings of the 14th International Middle East Power Systems Conference (MEPCON’10), Cairo, 19- 21 December 2010, 819-824. [3] Stephen, J.E., Kumar, S.S. and Jayakumar, J. (2014) Nonlinear Modeling of a Switched Reluctance Motor Using LSSVM—ABC. Acta Polytechnica Hungarica, 11, 143-158. [4] Tormey, D.P., Torrey, D.A. and Levin, P.L. (1990) Minimum Airgap-Permeance Data for the Doubly-Slotted Pole Structures Common in Variable-Reluctance-Motors. Industry Applications Society Annual Meeting, 1990, Conference Record of the 1990 IEEE, Seattle, 7-12 October 1990, 196-200. [5] Bal, G. and Uygun, D. (2010) An Approach to Obtain an Advisable Ratio between Stator and Rotor Tooth Widths in Switched Reluctance Motors for Higher Torque and Smoother Output Power Profile. Gazi University Journal of Sci- ence (GU J SCI), 23, 457-463. [6] Vijayakumar, K., Karthikeyan, R. and Arumugam, R. (2008) Influence of Soft Magnetic Composite Material on the Electromagnetic Torque Characteristics of Switched Reluctance Motor. IEEE Power India Conference on Power System Technology, 12-15 October 2008. [7] Chi, H.P. (2005) Flux-Linkage Based Models for Switched-Reluctance Motors. PHD Philosophy, National Cheng Kung University, Tainan. [8] Rebahi, F., Bentounsi, A., Lebsir, A. and Benamimour, T. (2014) Soft Magnetic Materials for Switched Reluctance  S. Saidani, M. Ghariani Machine: Finite El ement Analysis and Pe rspective. http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=7076953 [9] Sugawara, Y. and Akatsu, K. (2013) Characteristics of Switched Reluctance Motor Using Grain-Orien ted Electr ic Steel Sheet. 2013 IEEE ECCE Asia, Melbourne, 3-6 June 2013, 1105-1110. Appendix A FEMM Finite Element Method Magnetics (FE MM) is a finite element package for solving 2D planar and ax symmetric problems in low frequency magnetic and electrostatics. The program runs under runs under all versions Win- dows and XP. The Finite Element Method Magnetics (FEMM) is a program that can solve electromagnetic problems on 2D (two-dimensional planar). Thus, we can resolve linear and nonlinear magnetostatic, harmonic magnetic, linear electrostatic and steady state heat problems. The determination of magnetic characteristics faci- litates the optimization and control of switched reluctance machine. Appendix B 12/8 SRM Dimensions The dim e ns i ons of the switched rel uc t a nc e mot or are ne xt in Table B1: Table B1. Geometry of the 12/8 SVRM. SR machine model Stator outer diameter 137 ( mm) Stator inner diameter 85 ( mm) Stator teeth length 22 ( mm) Rotor outer diameter 42.48 (mm) Air gap 0.325 (mm) Number of turns 12 Stator pole arc 30(˚) Rotor pole arc 45(˚) Rotor teeth length 18.02 (mm)
|