Received September 2015

ABSTRACT

Dimensionality reduction is very important in pattern recognition, machine learning, and image recognition. In this paper, we propose a novel linear dimensionality reduction technique using trace ratio criterion, namely Discriminant Neighbourhood Structure Embedding Using Trace Ratio Criterion (TR-DNSE). TR-DNSE preserves the local intrinsic geometric structure, characterizing properties of similarity and diversity within each class, and enforces the separability between different classes by maximizing the sum of the weighted distances between nearby points from different classes. Experiments on four image databases show the effectiveness of the proposed approach.

Keywords:

Dimensionality Reduction, Manifold Learning, Variability, Trace Ratio

1. Introduction

Linear discriminant analysis (LDA) has been used widely in pattern recognition, machine learning, and image recognition [1] [2]. However, methods based on LDA techniques are optimal under Gaussian assumption [3] [4] and they effectively capture only the global Euclidean structure which may impair the local geometrical structure of data [5]-[7]. Recently, many approaches have shown the importance of local geometrical structure for dimensionality reduction and image classification. One of the most popular linear approaches is neighbourhoods preserving embedding (NPE) [8]. NPE aims to discover the local structure of the data and find projection directions along which the local geometric reconstruction relationship of data can be preserved.

Motivated by NPE, many discriminant approaches have been developed to further improve the data classification accuracy [9]-[11], such as margin fisher analysis (MFA) [12], locality sensitive discriminant analysis (LSDA) [13], locally linear discriminant embedding (LLDE) [14] and discriminative locality alignment (DLA) [15]. They preserve the intrinsic geometrical structure by minimizing a quadratic function.

The local variation of data characterizes the most important modes of variability of data and is important for data representation and classification [13] [16]-[19]. By maximizing the variance, we can unfold the manifold structure of data and may preserve the geometry of data. Structure of real-world data is complex and unknown, thus a single characterization may not be sufficient to represent the underlying intrinsic structure. It indicates that none of the aforementioned approaches can detect a stable and robust intrinsic structure representation.

In this paper, we propose a novel dimensionality reduction approach, namely discriminant neighbourhood structure embedding using trace ratio criterion (TR-DNSE) which explicitly considers the global variation, local variation, and local geometry. Experiments on four image databases indicate the effectiveness of TR-DNSE.

The remainder of this paper is organized as follows: Section 2 analyzes NPE. The idea of TR-DNSE is presented in Section 3. Section 4 describes some experimental results. Section 5 offers our conclusions.

2. Problem Statements

Given training data matrix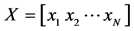, where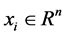 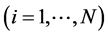denotes the i-th training data, 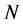is the number of training data. The objective function of NPE is [8]

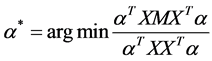(1)

where 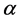denotes a projection matrix,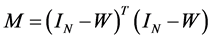. The elements 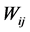in weight matrix 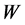denote the coefficients for reconstructing 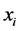from its neighbours, and can be calculated using [6].

The objective Function (1) can be decomposed into the following two objective functions:

(2)

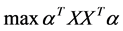(3)

The objective Function (2) aims to preserve the intrinsic geometry of the local neighborhoods [6] [8]. Given that all data points are centered, i.e., then the objective function (3) becomes

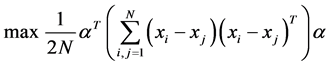(4)

Obviously, the objective function (4) which is equal to principal component analysis [2] aims to preserve the amount of variation of the values of data in the reduced space. However, it results in the following problems. It distorts the local geometry of data. As aforementioned analysis, the objective function (4) does not detect the local discriminating information among the nearby data points. Furthermore, NPE is an unsupervised approach, which does not make good use of the label information. It means that the generalization ability and stableness of NPE are not good enough.

3. Discriminant Neighborhood Structure Embedding Using Trace Ratio Criterion

3.1. The Objective Function for Dimensionality Reduction

Given training data matrix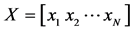, where denotes the i-th training data, N is the number of training data. denotes the class label of data. Motivated by manifold learning approaches

[6] [8] [18]-[20], we construct two adjacency graphs, namely geometry graph and variability graph, with a vertex set and two weight matrices and, to model the

local geometry and variation of data, respectively. The elements can be calculated by the following [6] [8]:

(5)

Subject to two constraints: first, enforcing if, second.

From the viewpoint of statistics, if two points and are very close to each other, (denotes the Euclidean distance between two vectors) is small, then the amount of variation of the values between them is also small. According to the analysis, the elements can be defined as follows:

(6)

where is k nearest neighbors of, is a positive parameter.

Moreover, motivated by LDA [1], we construct two global graphs and over the training data points to model the global variation, where, and if

, and and. is the number of the samples in the c-th class. The cor-

responding Laplacian matrices are denoted as and and, where is a diagonal matrix with the. As shown in [20], the between-class scatter matrix and the within-class scatter matrix can be rewritten as and.

The goal of TR-DNSE is to find projection directions such that both the amount of variation of values of data and local geometry can be preserved in the reduced space. A reasonable criterion for choosing a good map is to optimize the following four objective functions

(7)

(8)

(9)

(10)

where denotes the low-dimensional representation of,.

The objective function (7) ensures that the weights, which reconstruct the point by its same class datasets in the high dimensional space, will well reconstruct by the corresponding datasets points in the low dimensional space. The objective function (10) ensures the data points from the same class will be closer than data from different class. The objective function (9) emphasizes the large distance data pairs. Maximizing (8) is an attempt to ensure that, if the amount of variation of the values between and is large, then the amount of variation between and is also large. By simultaneously solving the four objective functions, we can obtain reasonable projection directions such that the variation and geometry of data can be well detected in low- dimensional space.

3.2. Optimal Linear Mapping

Suppose is a projection matrix, that is,. By simple algebra formulation, the objective function (7) and (8) can be reduced to

(11)

(12)

where is a N-dimensional identity matrix, , , is a symmetric matrix, is a diagonal matrix whose elements on diagonal are row or column sum of, i.e.. Finally, the optimization problem in ratio trace criterion can be reduces to finding:

(13)

3.3. Discriminant Neighborhood Structure Embedding Using Trace Ratio Criterion

Generally, the objected function (13) can be solved by using generalized eigenvalue decomposition. Given that the low-dimensional data representation is. is constrained to be in the linear subspace spanned by the

training data matrix. As shown in [21], we relax the hard constraint by substituting by and adding a regression residual term into the reformulated objective function. Then, is enforced to be close to. Specifically, we propose the following objective function:

(14)

(15)

where is a parameter to balance different terms and.

The above optimization problem in (14) is solved by Algorithm 1.

Explanation of Algorithm 1: With from the t-th iteration in (16), and are computed by maximizing the following trace different problem:

(16)

From (16), it can be observed that is a concave quadratic function with respect to the variable when the matrix is negative-definite. We set the partial derivative of with respect to the variable as zero, namely

(17)

where. In most cases, the matrix is negative-definite in our experiments, and is symmetric. Substituting in (16) by (17), then we get:

(18)

Algorithm 1. TR-DNSE algorithm.

In (18) we use the property. We also have because. Hence, is composed of the eigenvectors corresponding to the largest eigenvalues of the matrix , which explains the step 3 in Algorithm 1.

4. Experiments

In this section, we employ four widely used image databases (YALE, PIE, FERET and COLL20) to evaluate the performance of TR-DNSE and compare it with some classical approaches including Fisher face [22], MFA [12], LSDA [13], DLA [14] and LLDE [15] in the experiments. In classification stage, we use the Euclidean metric to measure the dissimilarity between two feature vectors and the nearest classifier for classification.

In our experiments, we first use the PCA to reduce the dimension of the training data by keep 80% - 97% energy of images. Likewise, we empirically determine a proper parameter within the interval and parameter t within the interval for the corresponding approaches.

The CMU PIE database [23] contains 68 subjects with 41368 face images as a whole. We select pose-29 images as gallery that includes 24 samples per person. The training set is composed of the first 12 images per person, and the corresponding remaining images for testing. Moreover, each image is of the size.

The Yale Face Database contains 165 grayscale images of 15 individuals. There are 11 images per subject. In our experiments the images are normalized to the size of. The first six images are selected to be the training data, and the rest for testing.

The FERET database [24] includes 1400 images of 200 individuals (each with seven images). All the images were cropped and resized to pixels. The images of one person are shown in Figure 1. In the experiment, we choose four images per person for training, and the remaining images from for testing.

The COIL20 image library contains 1440 gray scale images of 20 objects (72 images per object) [25]. Each image is of size. In the experiments, we select the first 36 images per object for training and the remaining images for testing.

Table 1 shows the best results of six approaches on four databases. Figure 2 plot the curves of recognition accuracy vs. number of projected vectors on four databases.

TR-DNSE has the best recognition accuracy than the other approaches in all the experiments. This is probably due to the fact that TR-DNSE preserves both the local geometry and variation of data, especially the discriminating information embedded in nearby data from different classes. Different from other approaches, TR-DNSE approach has a trace ratio criterion in solution. Related work demonstrates that the projection matrix solved

by using trace ratio criterion is generally better than the projection matrix solved by using generalized eigenvalue decomposition. By the trace ratio criterion, we can get an orthogonality projection matrix which helps to unfold the geometry and encode discriminating information of data. So the trace ratio criterion of TR-DNSE helps to get a better projection which results in better results.

5. Conclusion

Our method, TR-DNSE, which is proposed for dimensionality reduction, incorporates the intrinsic geometry, local variation, and global variation into the object function of dimensionality reduction. Geometry guarantees that nearby points can be mapped to a subspace in which they are still very close, which characterizes the similarity of data. Global variation and local variation characterize the most important modes of variability of patterns, and help to unfold the manifold structure of data and encode the discriminating information, especially the discriminating information embedded in nearby data from different classes. Experiments on four real-world image databases indicate the effectiveness of our TR-DNSE approach.

Cite this paper

Jing Wang,Fang Chen,Quanxue Gao, (2015) Discriminant Neighborhood Structure Embedding Using Trace Ratio Criterion for Image Recognition. Journal of Computer and Communications,03,64-70. doi: 10.4236/jcc.2015.311011

References