Journal of Computer and Communications
Vol.03 No.11(2015), Article ID:61280,6 pages
10.4236/jcc.2015.311010
Laplacian Maximum Margin Criterion for Image Recognition
Fang Chen1, Jing Wang2, Quanxue Gao1,2
1State Key Laboratory of Integrated Services Networks, Xidian University, Xi’an, China
2School of Telecommunications Engineering, Xidian University, Xi’an, China



Received September 2015

ABSTRACT
Previous works have demonstrated that Laplacian embedding can well preserve the local intrinsic structure. However, it ignores the diversity and may impair the local topology of data. In this paper, we build an objective function to learn the local intrinsic structure that characterizes both the local similarity and diversity of data, and then combine it with global structure to build a scatter difference criterion. Experimental results in face recognition show the effectiveness of our proposed approach.
Keywords:
Laplacian Embedding, Local Intrinsic Structure, Global Structure, Face Recognition

1. Introduction
Local geometric structure has received much attention in dimensionality reduction [1]-[3] and proven its effectiveness in image recognition, image retrieval, and document clustering [4]-[6]. One of the most popular approaches for this purpose is locality preserving projection (LPP) [1], a linear approximation of Laplacian eigenmap (LE) [2]. LPP seeks to find project axes along which the nearby data points in the high-dimensional space are mapped to nearby data points and well characterizes the local intrinsic structure of data. However, some nearby data points may come from different classes due to the uneven distribution in real-world applications. Thus, LPP does not encode the local discriminating information in this case.
Motivated by LPP and LDA, many local linear discriminant approaches have been developed for image classification, among which the most prevalent ones include MFA (Margin Fisher Analysis) [5] and LSDA (Locality Sensitive Discriminant Analysis) [6]. MFA and LSDA represent the intra-class compactness by LPP that maps nearby points from the same class to nearby points in the reduced space. However, LPP emphasizes the large distance pairs. Thus, it does not guarantee that the smaller the distance between two points in the local neighbourhood, the closer they should be embedded together in the reduced space, resulting in the impairment of local topology among nearby data with small distance [7]-[9]. Moreover, in the ideal case, the nearby data points from the same class are mapped to a single point in the reduced space by LPP. Thus, these discriminant approaches mainly capture the geometric properties of similarity, and ignores the diversity of the within-class data that is important for data recognition [7]-[10].
In real-world applications, the intrinsic structure of data is often complex, and only local or global structure is not sufficient to represent the underlying intrinsic structures. So, a reasonable approach should be the one that integrates global and local structures into the objective function of dimensionality reduction. Two of the most popular approaches are LapLDA [11] and semi-supervised discriminant structure by Laplacian Embedding (LE) [12]. As the previously discussed, the local geometry preserved by LE only considers the similarity and may impair the local topology of data [13] [14]. This may reduce the stableness and recognition performance of the algorithms.
In this paper, motivated by [14] [15], we build an objective function to learn the local intrinsic geometrical structure, which characterizes both the similarity and diversity of data, and then combine the local intrinsic structure with global intrinsic structure to build a scatter difference-based objective function, called Laplacian maximum margin criterion (LapMMC), for image recognition. Experiments on image databases demonstrate the effectiveness of LapMMC.
2. LapMMC
Given  data points
data points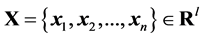 , we construct an adjacency graphs
, we construct an adjacency graphs 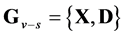 with a vertex set
with a vertex set 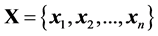 and a weight matrix
and a weight matrix 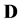 to model the intrinsic structure of data. Where the elements
to model the intrinsic structure of data. Where the elements 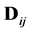 in
in 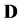 can be defined as follows
can be defined as follows
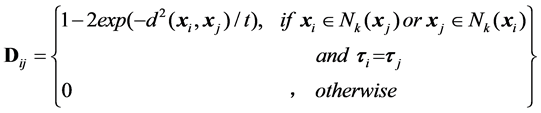 (1)
(1)
where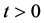 ,
, 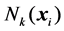 denotes the set of
denotes the set of 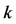 nearest neighbors of
nearest neighbors of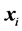 ,
, 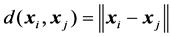 denotes the Euclidean distance between vectors
denotes the Euclidean distance between vectors 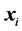 and
and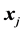 .
. 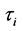 denotes the class label of data
denotes the class label of data
Now considering the problem of mapping the data points into a line, so that the local topology, which characterizes both the similarity and diversity of data, can be well preserved. As it happens, a reasonable criterion for choosing a good map is to optimize the following objective function

where 

In order to conveniently analyze the objective function (2), we only consider the nearby data, thus the objective function (2) can be also written as

where 



It is easy to see that the first term in (3) is PCA, which preserves the diversity of data, while the second term, which is just LE, preserves the similarity of data. Equation (3), i.e. Equation (2) seeks to find low-dimensional representations of

Figure 1. Difference between LE and our approach in preserving the local topology of data. (a) Two-dimensional data and one-dimensional embedding spaces obtained by LE and our approach, respectively; (b) One-dimensional embedded results obtained by LE; (c) One-dimensional embedded results obtained by our approach.
to see that, our approach well characterizes the local topology preserving at small distance data pairs in circle and thus well preserve the local intrinsic structure, which characterizes both the similarity, diversity of data and improves the stableness of the intra-class representation.
Suppose 


where 




The aim of LapMMC is to combine the local structure with global structure characterized by LDA. Thus, the objective function of LapMMC can be written as

where:

denote the between-class and within-class scatter matrix, respectively [7], 
The optimal projection vector 

Noting that, in many real world applications, 
3. Experiments
We evaluate the proposed approach LapMMC on image data databases (PIE and COIL20), and compare its performance with classical discriminant approaches including Fisherface [17], MFA [18], LSDA [19], LapLDA [20], SDA [11] and EFDC [14]. In the following experiments, we use the Euclidean metric and nearest classifier for classification due to its simplicity.
The CMU PIE database contains 68 subjects with 41368 face images as a whole. The face images were captured by 13 synchronized cameras and 21 flashes, under varying pose, illumination and expression. Each image is manually cropped and resized to 
The COIL20 image library [21] contains 1440 gray scale images of 20 objects (72 images per object). The images of each object were taken 50 apart as the object was rotated on a turntable. Each image is of size
Table 1 and Table 2 show the experimental results of different algorithms on the COIL20 and PIE database respectively. Figure 2 plots the recognition accuracy of seven methods vs. number of projection vectors on the PIE database and COIL20 database respectively.
From Table 1, Table 2 and Figure 2, we can see that, our approach LapMMC is markedly superior to other approaches. This is probably because that Fisherface may impair the local geometric structure of data, which is important for improving the recognition accuracy and stableness of the algorithm. MFA and LSDA preserve the local geometric structure by LPP and LPP only captures the similarity and ignores the diversity of data, which may impair the local topology of data [13]-[15]. Another reason may be that they neglect the global geometric structure of data, which is important for image recognition. Moreover, LapMMC obtains robustness intrinsic
Figure 2. The recognition accuracy of seven methods vs. features on the PIE database and COIL20 database.
Table 1. The top recognition accuracy (%) of seven methods on the COIL20 database and corresponding dimension of features.
Table 2. The top recognition accuracy (%) of seven methods on the PIE database and corresponding dimension of features.
geometrical structure characterized by both similarity and variability. Although LapLDA, EFDC and SDA take into consideration both the global and local geometric of data, the local geometric structure preserved by LapLDA and SDA neglect the diversity of data, and EFDC only considers the local diversity of data.
4. Conclusion
In this paper, we propose a novel linear dimensionality reduction algorithm called LapMMC, which integrates global and local geometrical structures into the objective function. To be specific, we construct an adjacency graph to learn the local intrinsic structure that characterizes both the local similarity and diversity of data, and then combine it with global structure to build a scatter difference criterion for dimensionality reduction. Experimental results on the COIL20 and PIE databases demonstrate the effectiveness of our approach.
Cite this paper
Fang Chen,Jing Wang,Quanxue Gao, (2015) Laplacian Maximum Margin Criterion for Image Recognition. Journal of Computer and Communications,03,58-63. doi: 10.4236/jcc.2015.311010
References
- 1. He, X., Yan, S., Hu, Y. and Zhang, H.J. (2003) Learning a Locality Preserving Subspace for Visual Recognition. IEEE International Conf. Computer Vision.
- 2. Belkin, M. and Niyogi, P. (2001) Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering. In: Advances in Neural Information Processing Systems.
- 3. Xu, Y., Feng, G. and Zhao, Y. (2009) One Improvement to Two-Dimensional Locality Preserving Projection Method for Use with Face Recognition. Neurocomputing, 73, 245-249. http://dx.doi.org/10.1016/j.neucom.2009.09.010
- 4. Cai, D., He, X. and Han, J. (2005) Document Clustering Using Locality Preserving Indexing, IEEE Trans. Knowledge and Data Engineering, 17, 1624-1637. http://dx.doi.org/10.1109/TKDE.2005.198
- 5. Yan, S., Xu, D., Zhang, B., Zhang, H., Yang, Q. and Lin, S. (2007) Graph Embedding and Extensions: A General Framework for Dimensionality Reduction. IEEE Trans. Pattern Analysis and Machine Intelligence, 29, 40-51. http://dx.doi.org/10.1109/TPAMI.2007.250598
- 6. Cai, D., He, X., Zhou, K., Han, J. and Bao, H. (2007) Locality Sensitive Discriminant Analysis. In: Proc. International Joint Conf. Artificial Intelligence (IJCAI’07).
- 7. Gao, Q., Xu, H., Li, Y. and Xie, D. (2010) Two-Dimensional Supervised Local Similarity and Diversity Projection. Pattern Recognition, 43, 3359-3363. http://dx.doi.org/10.1016/j.patcog.2010.05.017
- 8. Luo, D., Ding, C., Nie, F. and Huang, H. (2011) Cauchy Graph Embedding. Int. Conf. Machine Learning.
- 9. Gao, Q., Zhang, H. and Liu, J. (2012) Two-Dimensional Margin, Similarity and Variation Embedding. Neurocomputing, 86, 179-183. http://dx.doi.org/10.1016/j.neucom.2012.01.023
- 10. Weinberger, K.Q. and Saul, L.K. (2006) An Introduction Tonon-linear Dimensionality Reduction by Maximum Variance Unfolding. In: Proc. the 21th AAAI, 1683-1686.
- 11. Cai, D., He, X. and Han, J. (2007) Semi-Supervised Discriminant Analysis. IEEE Int. Conf. Computer Vision, Rio de Janeiro, 1-7. http://dx.doi.org/10.1109/iccv.2007.4408856
- 12. Belkin, M. and Niyogi, P. (2001) Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering. In Advances in Neural Information Processing Systems, MIT USA, 585-591.
- 13. Luo, D., Ding, C., Nie, F. and Huang, H. (2011) Cauchy Graph Embedding. Proc. Int. Conf. Machine Learning, Bellevue, 1-8.
- 14. Gao, Q., Liu, J., Zhang, H., Hou, J. and Yang, X. (2012) Enhanced Fisher Discriminant Criterion for Image Recognition. Pattern Recognition, 45, 3717-3724. http://dx.doi.org/10.1016/j.patcog.2012.03.024
- 15. Gao, Q., Gao, F., Zhang, H., Hao, X. and Wang, X. (2013) Two-Dimensional Maximum Local Variation Based on Image Euclidean Distance for Face Recognition. IEEE Trans. Image Processing, 22, 3807-3817. http://dx.doi.org/10.1109/TIP.2013.2262286
- 16. Belhumeur, N., Hepanha, J.P. and Kriegman, D.J. (1997) Eigenfaces vs. fisherfaces: Recognition Using Class Specific Linear Projection. IEEE Trans. Pattern Analysis and Machine Intel-ligence, 19, 711-720. http://dx.doi.org/10.1109/34.598228
- 17. Belhumeur, N., Hepanha, J.P. and Kriegman, D.J. (1997) Eigenfaces vs. Fi-sherfaces: Recognition Using Class Specific Linear Projection. IEEE Trans. Pattern Analysis and Machine Intelligence, 19, 711-720. http://dx.doi.org/10.1109/34.598228
- 18. Yan, S. Xu, D., Zhang, B., Zhang, H., Yang, Q. and Lin, S. (2007) Graph Embedding and Extensions: A General Framework for Dimensionality Reduction. IEEE Trans. Pattern Analysis and Machine Intelligence, 29, 40-51. http://dx.doi.org/10.1109/TPAMI.2007.250598
- 19. Cai, D., He, X., Zhou, K., Han, J. and Bao, H. (2007) Locality Sensitive Discriminant Analysis. In: Proc. Int. Joint Conf. Artificial Intelligence, San Francisco, 708-713.
- 20. Chen, J., Ye, J. and Li, Q. (2007) Integrating Global and Local Structures: A Least Squares Framework for Dimensionality Reduction. IEEE Conf. Computer Visual and Pattern Recognition, Minneapolis, 1-8.
- 21. http://www1.cs.columbia.edu/CAVE/software/softlib/coil20.php






