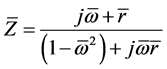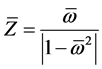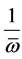World Journal of Engineering and Technology
Vol.03 No.04(2015), Article ID:61263,5 pages
10.4236/wjet.2015.34B004
Existence Region of the Module of a Parallel Contour Impedance and Phase Charts
N. A. Parfentiev, E. N. Parfentieva
All-Russian Institute of Cinematography, Moscow, Russia



Received 22 October 2015; accepted 13 November 2015; published 20 November 2015

ABSTRACT
The special point is found in frequency characteristics of one model of an oscillatory contour about which it wasn’t reported in scientific literature earlier. The point settles down at a frequency, the smaller resonant frequency of a contour. The module of an impedance doesn’t depend on the size of active resistance at this frequency. Physical interpretation of the phenomenon doesn’t exist at the moment. This article is continuation of the already research, results of calculations of existence region of the impedance module of an oscillatory contour are for the first time given in it and phase charts are provided. Two models of an oscillatory contour are considered. Existence region of the module of an impedance are essentially different for the considered models. Phase charts of an impedance are calculated depending on relative frequency. Results of research can be used in the electrician and the electronic engineer and manual for profound studying of electrical equipment.
Keywords:
Oscillatory Contour, Phase Chart, Impedance, Resonance of Currents

1. Introduction
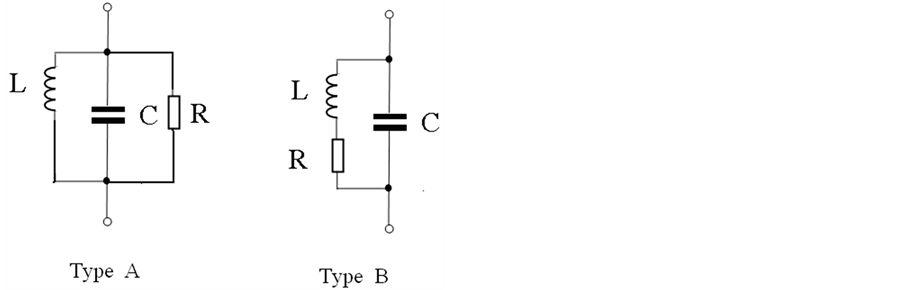
One of the most widespread elements of radio engineering devices is the oscillatory contour. Electrical circuit tutorials the type of a parallel contour (Figure 1(B)) is considered often. The analysis of such chain is limited to the statement that its resonant frequency decreases with growth of size of active resistance (unlike model of a contour (Figure 1(A)).
Results of research of contour frequency characteristics (type B, more realistic, then type A) were presented [1]. The special point or a point of stability is found in frequency characteristics of the module of complex resistance of this chain. Special point settles down at a frequency lower then the frequency of resonance. The chain module of resistance doesn’t depend on the size of active resistance.
On the basis of the found effect the mechanical model [2] was offered. The module of mechanical resistance of the model also didn’t depend on the value of coefficient of viscosity at a certain frequency.
This article is continuation of the already begun research. Results of calculations are given existence region of
Figure 1.Two models of an oscillatory contour.
the relative module impedance. Circular charts of contour various models are given in the wide range of frequencies. Formulas are defined for the dependence of shift and radius of a phase semi-circle.
1.1. Analysis of Model A
The model of a contour (Figure 1(A)) is formed from in parallel the connected elements. The impedance (in a dimensionless form) of a chain can be presented in the following form:
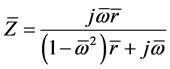
where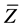 ―relation of the impedance to the characteristic resistance of a contour, equal
―relation of the impedance to the characteristic resistance of a contour, equal ,
,
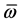 ―the frequency relation to resonant frequency,
―the frequency relation to resonant frequency,
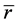 ―the relation of active resistance to the contour characteristic resistance contour.
―the relation of active resistance to the contour characteristic resistance contour.
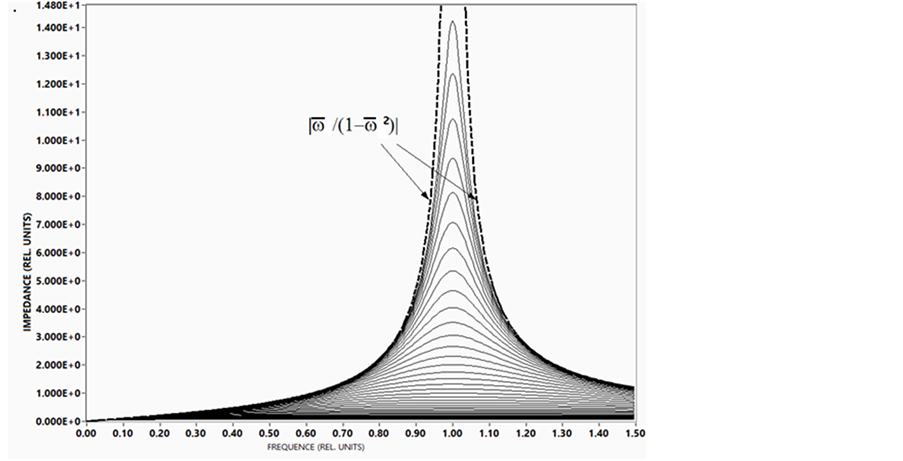
Existence region of the impedance module (type A) is presented on Figure 2.
The existence region of the impedance module is limited from below by abscissa axis (at  = 0), and from above by the asimtote
= 0), and from above by the asimtote
 ,
,
corresponding 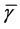 → ∞, noted by the dashed line on the picture. Curves of an impedance come nearer to the second asimtota, differing from them in the most part in the area of a maximum.
→ ∞, noted by the dashed line on the picture. Curves of an impedance come nearer to the second asimtota, differing from them in the most part in the area of a maximum.
The phase surface of model A is presented on Figure 3. It formed by the semi-circular charts of an impedance changing dependences on relative frequency. According to Figure 3 semi-circular charts include the point corre- sponding zero an impedance.
At each frequency the phase chart represents a semi-circle the radius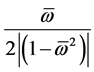 , which center is displaced at
, which center is displaced at
a radius size in a positive or negative side depending on a difference sign between this and resonant frequencies.
1.2. Analysis of Model B
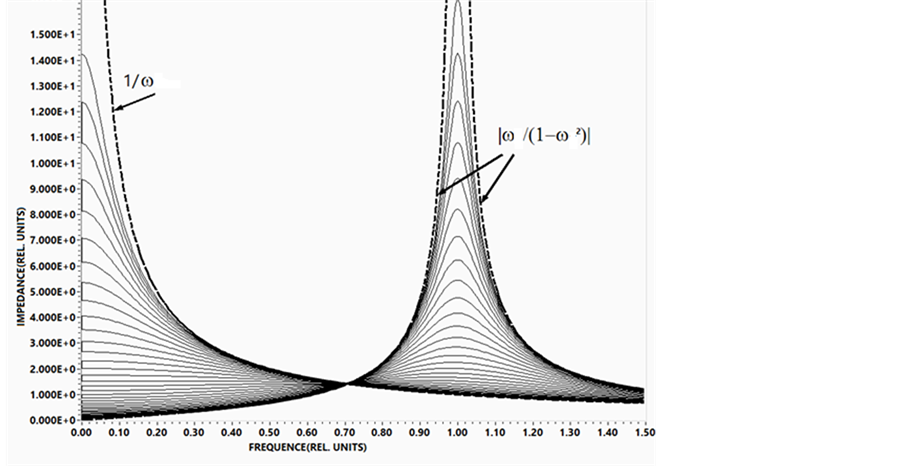
The existence region of the impedance module (Type B) is presented on Figure 4. This contour consists of the condenser and the inductance coil, modelled by the consistently connected active resistance and reactance. The impedance of a such contour can be presented in the form:
where  ,
,  and
and 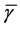 ―such dimensionless sizes of an impedance, frequency and active resistance, as for a contour of type 1A.
―such dimensionless sizes of an impedance, frequency and active resistance, as for a contour of type 1A.
Figure 2. Existence region of the impedance module (Type A).
Figure 3. Phase charts of a parallel contour (type A).
Figure 4. Existence region of the impedance module 1B.
The frequency characteristic of an impedance, significantly differs from the dependence on the Figure 2. The existence region of the impedance module is limited by two asymptotes noted on the figure by dashed lines:
1) asimtote
(at 
2) asimtote
Corresponding 
All the curves of an impedance module (and asymptotes) have the general point with value of the relative module 
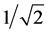
The phase surface of the impedance (type B) is given (Figure 5) depending on the frequency. The chart is
formed by semi-circles which radius is equal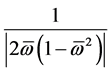
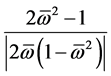
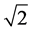
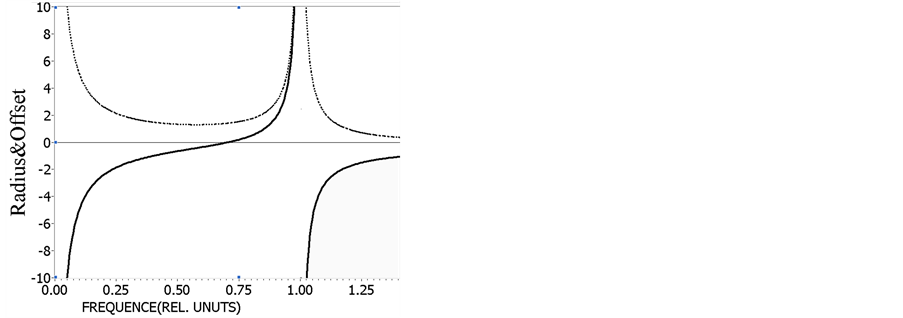
Radius and offset of a phase semi-circle is received depending on the relative frequency for model of a contour type B (Figure 6). (Offset-solid line, radius-dashed line). Line offset crossed abscissa in special point.
All calculations and plotting were performed using the program LabView 8.0.
2. Conclusions
Existence region of the impedance module are various for contours of different types. The lower bound of the module is defined for the contour of type B. In the result of research of the surfaces formed by the phase charts it is shown that charts have a semi-circle form in the wide range of frequencies. Dependence of the radius and shift of the circular charts is received for all range of frequencies. Basic distinction of the thephase charts is revealed for the contour different models.This results is obviously important for researches of the chains containing the oscillatory contour and also when studying electrical equipment and radio engineering.
Figure 5. Surface of the phase charts (type B).
Figure 6. Radius and shift of phase charts for model type B.
The founded effect may find application in measurement technology in the development of new techniques, for example, additional monitoring of the resonant frequency or measurement of the reactive component of the high-resistance resistors
Cite this paper
N. A. Parfentiev,E. N. Parfentieva, (2015) Existence Region of the Module of a Parallel Contour Impedance and Phase Charts. World Journal of Engineering and Technology,03,16-20. doi: 10.4236/wjet.2015.34B004
References
- 1. Parfentyev, N.A., Parfentyeva, E.N. and Sevastyanov, S.I. Pecularity of Frequency Characteristics of a Parallel Oscil-latory Contour. News of Higher Education Institutions, Electronics No. 62014, 110.
- 2. Parfentyev, N.A., Parfentyeva, N. and Trukhanov, S.V. (2014) About a Special Point of Frequency Characteristics of Oscillatory Systems. Natural and Technical Science, 9-10, 31.