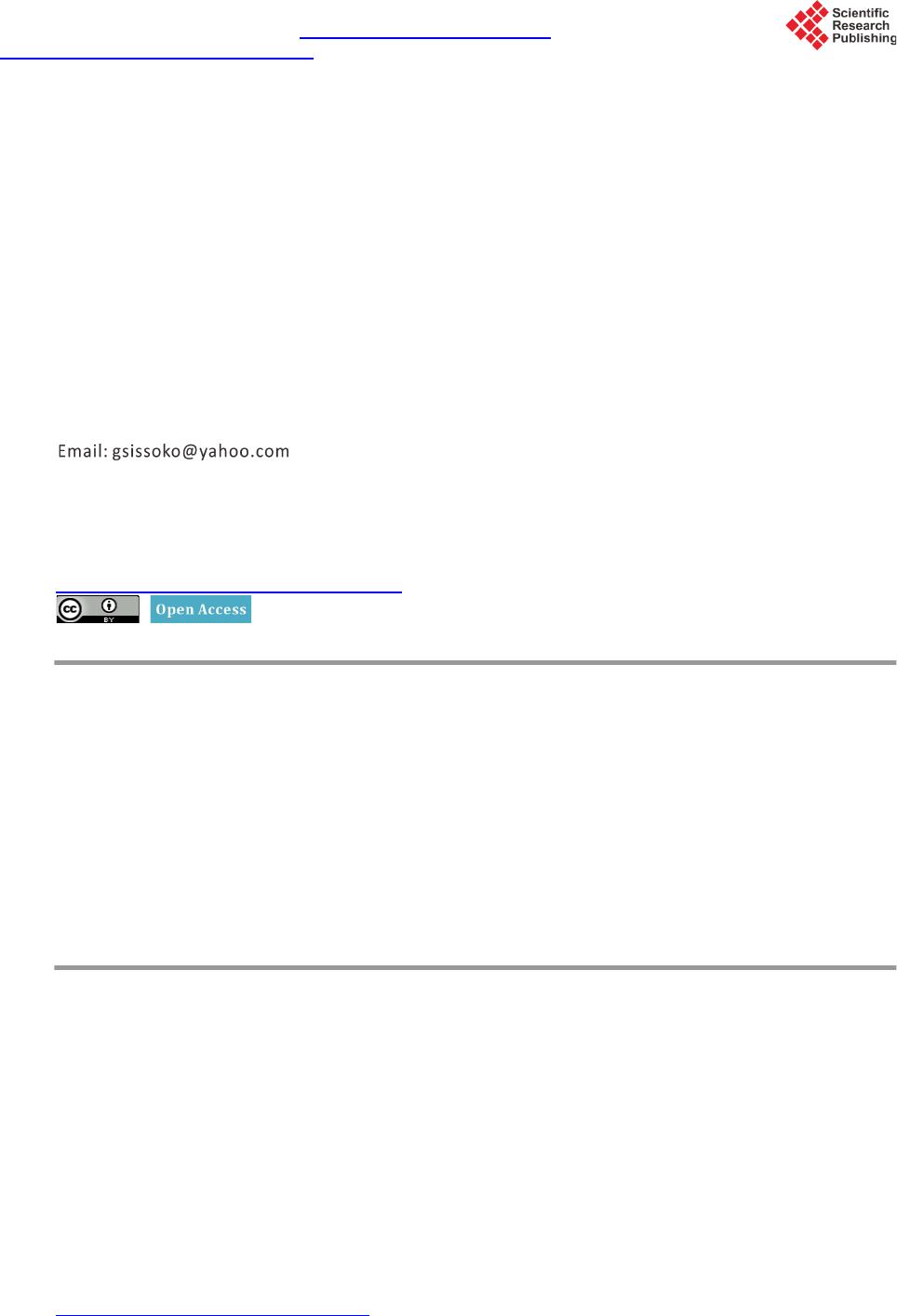
 World Journal of Condensed Matter Physics, 2015, 5, 284-293 Published Online November 2015 in SciRes. http://www.scirp.org/journal/wjcmp http://dx.doi.org/10.4236/wjcmp.2015.54029 How to cite this paper: Mbodji, S., Zoungrana, M., Zerbo, I., Dieng, B. and Sissoko, G. (2015) Modelling Study of Magnetic Field’s Effects on Solar Cell’s Transient Decay. World Journal of Condensed Matter Physics, 5, 284-293. http://dx.doi.org/10.4236/wjcmp.2015.54029 Modelling Study of Magnetic Field’s Effects on Solar Cell’s Transient Decay Senghane Mbodji1, Martial Zoungrana2, Issa Zerbo2, Biram Dieng1, Gregoire Sissoko3 1Department of Physics, Alioune DIOP University of Bambey, Bambey, Seneg al 2Laboratoire d’Energies Thermiques et Renouvelables (L.E.T.RE), Departement de Physique, U.F.R-S.E.A, Universite de Ouagadougou, Ouagadougou, Burkina Faso 3Laboratory of Semiconductors and Solar Energy, Department of Physics, Faculty of Science and Technology, Cheikh Anta Diop University, Dakar, Senega l Received 19 October 2015; ac cep ted 15 November 2015; published 18 November 2015 Copyright © 2015 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativ ecommon s.org/l icens es/by/4.0/ Abstract Experimental setup of transient decay which occurs between two steady state operating points is recalled. The continuity equation is resolved using both the junction dynamic velocity (Sf) and back side recombination velocity (Sb). The transient excess minority carriers density appears as the sum of infinite terms. Influence of magnetic field on the transient excess minority carriers density and transient photo voltage is studied and it is demonstrated that the use of this technique is valid only when the magnetic field is lower than 0.001 T. Keywords Solar Cell, Recombination Par ameter s, Magnetic Field 1. Introduction Recombination parameters of solar cells are often investigated considering the steady state [1]-[4] or one of the many transient decay techniques [5]-[10]. As regards the transient states, we can cite the electroluminescence emission measurements [11], the frequency modulation approach [12], the open circuit voltage decay (OCVD) techn ique whic h is the mo st po pula r, t he pho toc urre nt de cay ( PCD) method [13], the ste pped light -ind uced tran- sient measurements of photocurrent and voltage (SLIM-PCV) [14] , the microwave photocurrent decay (MW- PCD) [15], the well-known transie nt state ope r a ting between two steady state rea l operating points [16], etc. The OCVD is usually combined to PCD method for determining, simultaneously, the lifetime and the consid- ered surface recombination velocity (S) of materials and photovoltaic structures [13]. T he SLIM -PCV is a valid 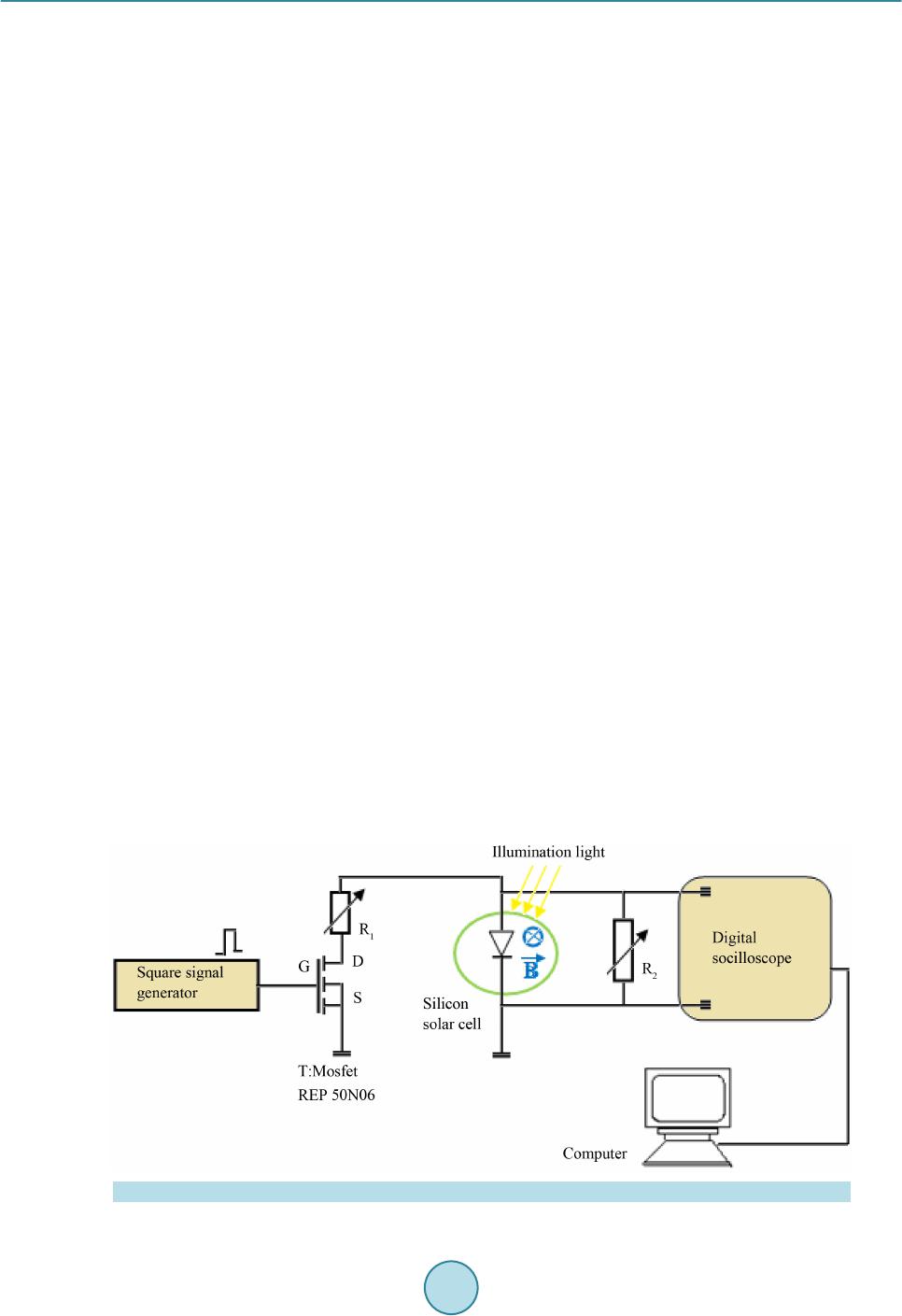 S. Mbodji et al. method to measure electron diffusion coefficient (D) and electron lifetimes of dye-sensitized solar cells (DCS) [14]. Respecting to the transient state operating between two steady state real operating points, it has been carried out on a solar cell placed in a fast-switch-interrupted circuit and submitted to a co nstant multispectral ill umina- tion. The transient decay occurs between two steady states through operating points depending on two variables resistors; this technique allows obtaining a transient decay at any operating point of the solar cell I-V curve (from the short circuit to the op en one) . By combi ning e xper imental and ca lculatio n re sults o f the phot o volta ge transient decay response, the eigen value ω0 of the fundamental decay mode and the decay time constant, the minority carrier lifetime (τ) is determined. The effective minority carrier diffusion len gth (Leff), the juncti on dy- namic velocity (Sf) and the backside recombination velocity (Sb) are then deduced [10]-[17]. Solar cells have seen remarkable improvements despite of some internal and external factors affecting their efficiency. Among internal factors, we can cite the grain boundary recombination velocity (Sgb) [1]-[3] [17] , t he intrinsic junction recombination velocity (Sf0) [1]-[3] [8]-[10] [15] [17] related to the shunt resistance (Rsh) [2]-[18] due to losses at the junction, the series resistance (Rs) [2] [16] [18], and the back side recombination velocity (Sb) which quantifies the rate at which excess carriers are lost at the back surface of the solar cells [1]-[3] [8]-[10] [16] [ 17]. One of the external factors affecting efficiency of the solar cell, is the magnetic field which has various ori- gins [19]. Depend ing on the position of the solar cell and the emittin g source of the magn etic field, one can note some effects on the solar cells devices. That is why some works concerning influence of magnetic field on solar cells are done [12] [19] [20]. It is sho wn tha t, t he pea k po wer (Pm), the shor t-circ uit p hoto curr ent, the p hot o vol t- age and the solar cell diffusion capacitance which is reduced to the Shockley’s depletion model decrease with the magnetic field when the solar cells is operating in steady state [21]. It has been also proved that under fre- quency mod ulation, the elec tron intri nsic mobilit y (µ), the d iffusion coe fficient (D), and t he d iff usio n le ngth ( L) decrease when the silicon solar c e ll is both under applied magnetic field and frequency illumination mode [12]. In this present work, we are interesting of solar cell under magnetic field and in transient decay which occurs between two steady state operating points. We examine magnetic field effects on the eige nva lue ω 0 of the fun- damental decay mode, the excess minority carriers and the photo voltage decay. 2. Materials and Methods 2.1. Experimental Setup and Working Principle of the Transient Decay Occurring between Two Steady State Operating Points The experimental setup (Figure 1) includes a square signal generator (BRI8500) which pilots a Mosfet transistor type RFP50N06, two variables resistors R1 and R2, a silicon sola r cell submitted to a cons tant multispectral ill u- mination, a digital oscilloscope, and a microcomputer. The tra nsient decay occurs according to the following procedure, described below. Figure 1 . E xperimental setup [ 10].  S. Mbodji et al. At time t < 0 the solar cell is in parallel with the resistor R2 giving the pote ntial V2 co rr e spo ndi n g to the ste ady state oper ating point F2. At time t = 0, the fast switch begins turning on a nd a t time t > 0 is completely turned on. It then connects the resistor R2 in parallel with the solar cell and the resistor R1. T he vol tage V2 drops from V2 to V1 corresponding to the new steady state operating point F1 as it can be seen on Figure 2. This experience give an experimental photo voltage decay V(t) which occurs between F2 and F1. Thi s exp er i- ence is innovative because not involving light pulse and also does not consider only the open circuit photo volt- age or the short-circuit photo current conditions as usually done in the OCVD and both the OCDV and PCD measurement techniq ues [13]. Figure 2 shows also ho w the I-V curves and then, the operating points are affected by the magnetic field as sho wn in [21]. 2.2. Theory A schematic dia gram of the conside red silicon solar cell u nder a magnetic field with its different coor dinates is given in Figure 3. The illumination was assumed to be uniform, such that the carrier generation rate depended only on depth (z) in the base and was expressed as: ( ) ( ) 3 1 exp ii i G zabz = = ⋅− ∑ (1) Coefficients ai and bi are deduced from modelling of the generation rate considered for over all the solar ra- diation spectr um [17]. Figure 2 . Illuminated I-V curve under constan t magnetic field ( B3 < B2 < B1) with two specific oper- ating points [9] [10] . Figure 3 . Illuminated silicon solar cell under magnetic field.  S. Mbodji et al. Also, the contributions of emitter and space charge region were neglected, the injection level is constant and the analysis wa s limited to the base region of t hick ness, H = 200 μm. Hence, the transient excess minority carrier distribution in the cell base was derived by solving the 1D continuit y equation [10] [16] : ( )()( ) 2 * 2 ,, ,zt ztzt Dt z δδ δ τ ∂∂ ⋅ −= ∂ ∂ (2) whe re , the diffusion constant under magnetic field was expressed as [22]: (3) µ is the mobilit y of excess minority carriers in the base [22]. D and τ are respectively, solar cell minority carrier diffusion constant coefficient and carrier lifetime [10]. Equation (2) is resolved using below boundary conditions [1]-[3] [8]-[10] [ 16 ] [17]: - At the j uncti on, z = 0 (n-p interface): ( )( ) 0 ,0, . z zt DSf t z δδ ∗ = ∂ ⋅=⋅ ∂ (4) - And at the back side of the silicon solar cell, z = H [1]-[3] [8]-[10] [16] [17] ( )( ) ,,. xH zt DSbH t z δδ ∗ = ∂ ⋅ =−⋅ ∂ (5) Sf is define d as the J unc t io n d yna mi c vel oc it y [23]. It is the sum of two ter ms which tradu ce lo sses at junctio n and the collected excess minority carriers. Sf was called junction recombination velocity in our previous papers [1]-[3] [8]-[10] [16] [17] [22] . Sb is the back surface recombination velocity which traduces excess minority carriers lost at rear side of the solar cell [1]-[3] [8]-[10] [16] [17]. Equations (4) and (5) form a STURM Liouville’s system of equations [9] whose solutions are separable vari- ables of space and time. Thus, we can set: (6) Z(z) is the space function and T(t), the time function are written, respectively: ( ) 12 cos sin zz Zz AA DD ωω ∗∗ ⋅⋅ =⋅ +⋅ (7) and ( )() 21 0 expTt Tt ωτ =⋅− +⋅ (8) with: , the decay time constant and where ω > 0. The bo undar y conditions give: (9) and ( ) * 2 tg D SfSb H DSf Sb D ω ω ω ∗ ∗ ⋅+ = ⋅−⋅ (10) with:  S. Mbodji et al. π11 0, π;π. 2 22 Hnn D ω ∗ ⋅ ∈ −+ (11) n is a natural number and: (12 ) Equation (10) is transcendental equation (of infinite number of positive roots), and was solved by Newton- Raphson numerical method [24] to obtain the allowed solutions ω n. In other works which are based to OCDV method, solution from the work of Rose and Weaver [6] are adopted. ω 0 is the eigenvalue of the fundamental decay mode and ω n are the eigenvalues of the harmonic of order n decay mode, when n > 0. Hence, we can see that A and B have discrete values and were finally calculated by normalization and Fourier transform [24]. Thus, the transient excess minority carriers density appears as the sum of infinite terms δ n(z;t). Each term, δ n(z;t), is the contribution of order n to the transient excess minority carriers density. When n is equal to zero, we have the first term, δ 0(z;t), corresponding to fundamental mode which i s charac- terized by ω 0 and whe n n > 0, δ n(z;t) corresponds to harmonic of order n characterized by ω n. δ n(z;t) is expressed as: ()( )( ) , 1 ,0 exp. n nncn ztZ zTt δτ = − (13) The transient excess minority carriers density is: (14) is discrete decay time constant. The magnetic field effects on the eigenvalue of the fundamental decay mode and on the eigenvalues of the harmonic of order n decay mode are given on Tables 1-3. Tables 1 -3: ra nge va lue s of eigenvalue ω 0 of the fu nda ment al d eca y mod e, e ige nval ues ω n (n > 0 ) of t he har- monic of order n decay modes and corresponding decay time constant modes: We can note that, the eigenvalue ω 0 of the fundamental decay mode, the eigenvalues ω n (n > 0) of the har- monic of order n decay mode decrease with the magnetic field, conversely, the different corresponding decay time constants modes increase with the magnetic field. Table 1. B = 0 T. n 0 1 2 3 4 ω n (s−1/2) 691 1409 2154 2918 3694 τ c,n (µs) 1.430 0.450 0.200 0.110 0.070 Table 2. B = 0.001 T. n 0 1 2 3 4 ω n (s−1/2) 502 1016 1 544 2 084 2 630 τ c,n (µs) 2.200 0.810 0.380 0.220 0.140 Table 3. B = 0.01 T. n 0 1 2 3 4 ω n (s−1/2) 78 156 234 313 470 τ c,n (µs) 4.380 4.050 3.610 3.120 2.250 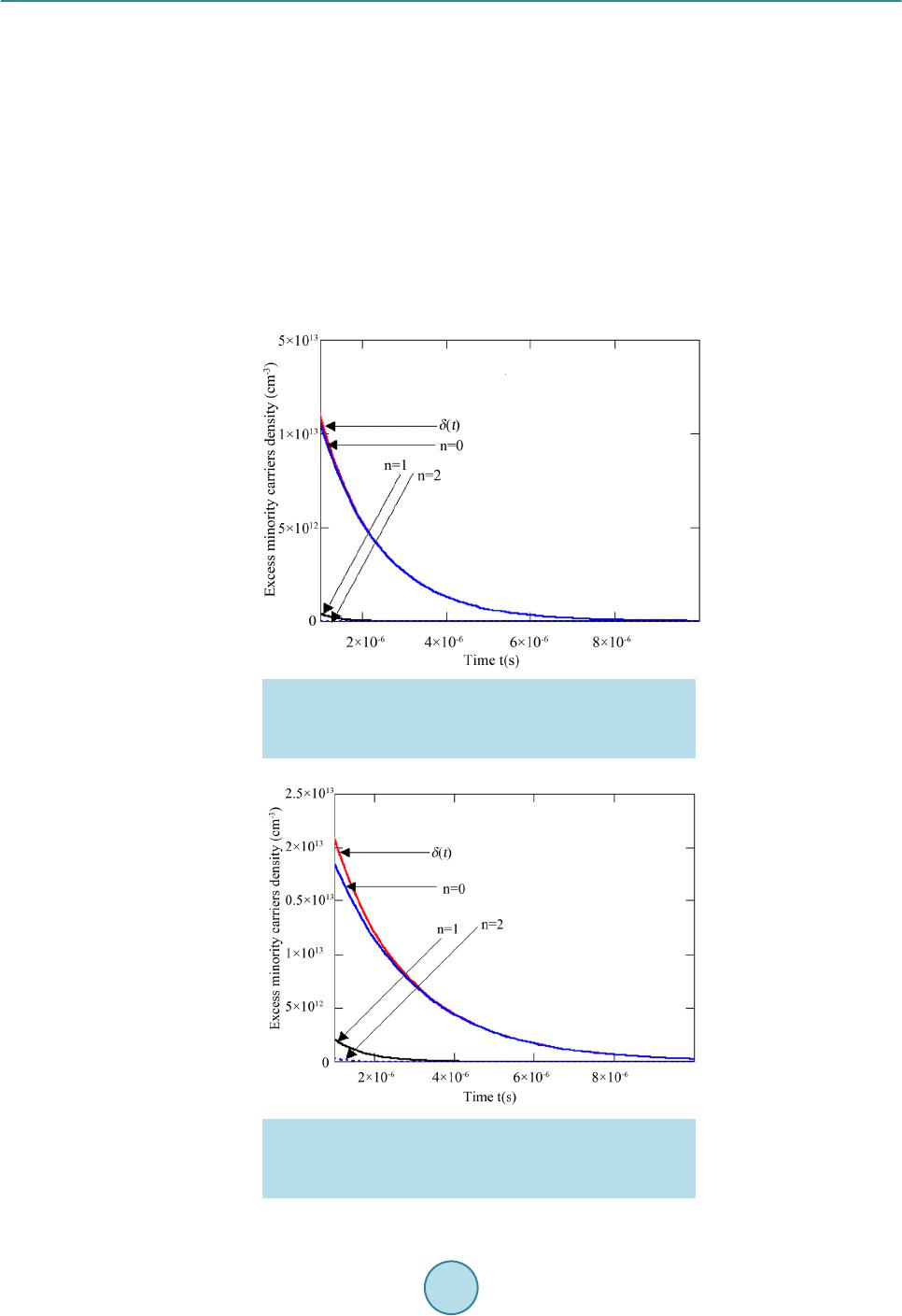 S. Mbodji et al. 3. Results and Discussion 3.1. Transient Excess Minority Carriers Density For the simulation process, all the key equations were input into MathCAD software. With base thickness and doping density fixed, the eigenvalues ω n were determined by numerical solution of Equations (9) and (10) using Newton-Rap hson met hod [23]. Compared to both OCDV and PCD techniques [13], where eigenvalues are calculated considering two operating points (open circuit and short-circuit), our method does not related to any operating point [10]-[16]. For the simulated modeling analyses, the transient excess minority carriers density was expressed as a func- tion of magnetic field B, the juncti on dyna mic velo city (Sf), the back side reco mbination velocity (Sb), the har- monic of order n, and the ti me (t). Figures 4-6 show plots of the excess minority carriers density versus both the time and the magnetic field B which takes 0, 0.001 T and 0.01 T, respectively. Figure 4. Excess minority carriers density versus the time t(s) when the magnetic field B = 0 T with H = 200 µm, D* = 26 cm2∙s−1, τ = 4.5 µs, µ = 1000 cm2∙V−1∙s−1, Sf = 4 × 105 cm∙ s−1 and Sb = 8 × 103 c m∙s−1. Figure 5. Excess minority carriers density versus the time t(s) when the magneti c field B = 0.001 T with H = 200 µm, D* = 13 cm2∙s−1, τ = 4.5 µs, µ = 1000 cm2∙V−1∙s−1, Sf = 3 × 105 cm∙s−1 and Sb = 5 × 103 c m∙s −1. 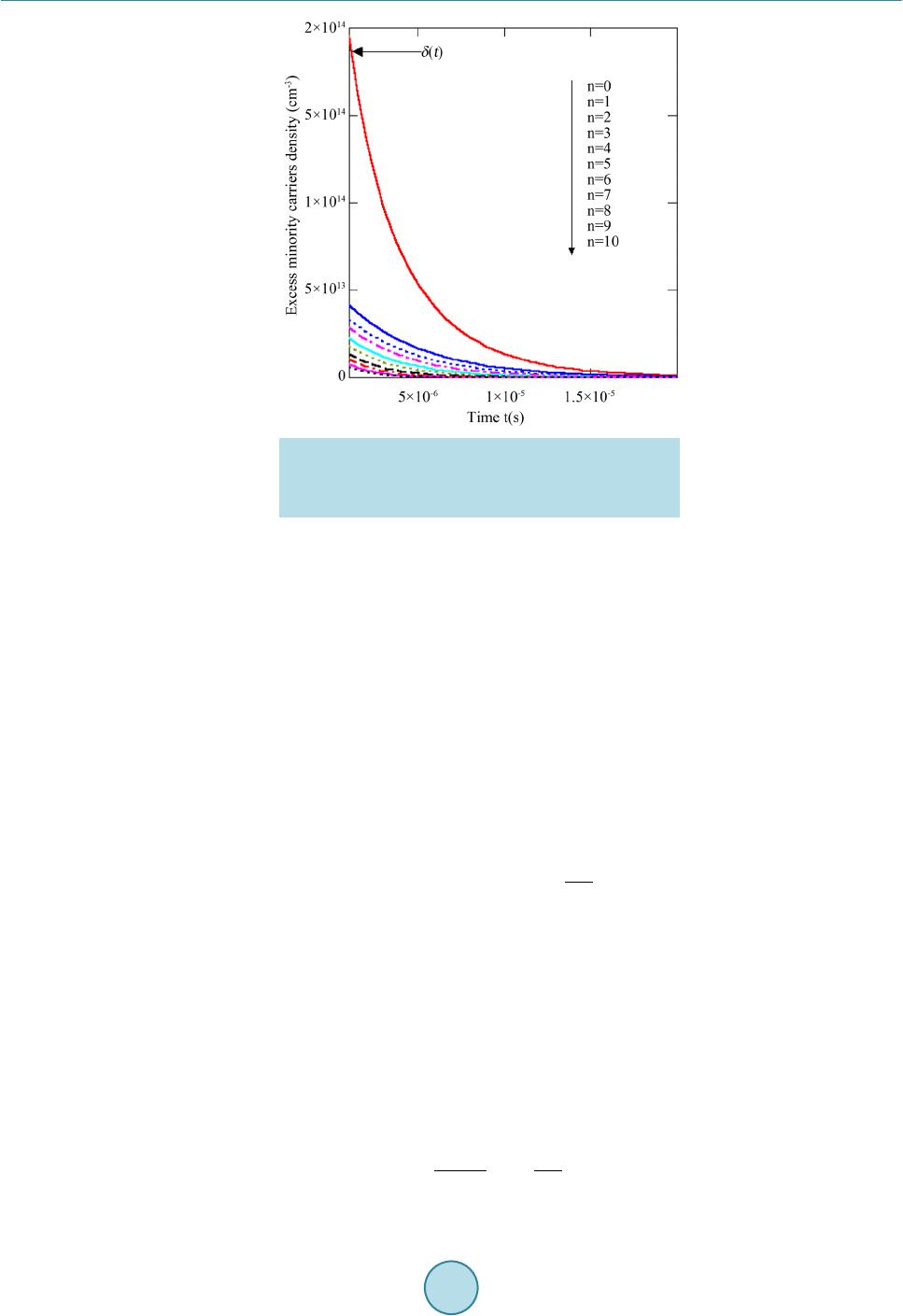 S. Mbodji et al. Figure 6. Excess minority carriers density versus the time t(s) when the magnetic field B = 0.01 T with H = 200 µm, D* = 0.257 cm2∙s−1, τ = 4.5 µs, µ = 1000 cm2∙V−1∙s−1, Sf = 2 × 103 cm∙s −1 and Sb = 700 cm∙s−1. Without magnetic field, it has been remarked that the excess minority carriers density is o btained by the fun- damental mode. The contributions of the harmonic of order n is neglected as found by [9] [10]-[16] . Figure 5 is the plot of the transient excess minor ity carriers density when B = 0.001 T. When the applied magnetic field is B = 0.001 T, we noted two situatio ns. The first is when t < 2 µs, the har- monics of order 1 and 2 aren’t null but would be neglected while the fundamental mode reaches to the transient excess minority carriers density. When t > 2 µs, the transient excess minority carriers density is equal to the contribution of fundamental’s mode. In Figure 6, we show the variation of t he transient excess minority carriers as the function of time when B = 0.01 T. For B = 0.01 T, the excess minority carriers density cannot be taken to be equal to the contribution of the fundamental mode. The contribution of all terms are important. Hence, for low magnetic field (B < 10−3 T) we concluded that the transient excess minority carriers density is given by the contribution of the fundamental mode. Thus, the transient excess minority carriers density, at the junction, is expr essed as: ()()( )( ) 0 00,0 1 0,0exp. c ttZ zTt δδ τ = =− (15) For high val ues of ma gnet ic fi eld ( B > 10−3 T), the transient excess minority carriers density is calculated tak- ing into account for all ter ms. So, both the OCDV and PCD method [13] which is used to deter mine the lifetime and the surface recombination velocity and the transient decay technique which occurs between two steady state operating cond itions [9] [10]-[15] developed for investigation of recombination parameters wouldn’t be valid in this range values of magnetic field. 3.2. Transient Photo Voltage Decay Since the excess minority carrier density and the charge carriers gap at the junct ion are kno wn, fro m the Boltzmann relation we can derive the photo voltage transient decay across the junction as: ( )( ) 0, lnexp . TT tV Vt VV δ δφ ∆ = ⋅ (16)  S. Mbodji et al. Figure 7. Ttransient photo voltage decay versus the time t(s) with H = 200 µm, τ = 4.5 µs, µ = 1000 cm2∙V−1∙s−1, and ∆V = 0.01 V. δφ is charge carriers gap at the junction [10] and VT is the thermal voltage. The transient photo voltage decay was also simulated by analysing dependence on magnetic field. Figure 7 shows plot of the transient photo voltage decay, at H = 200 µm, τ = 4.6 µs and ∆V = 0.01 V, with the magnetic field taking 0 T, 0.001 T, 0.01 T and 0.1 T, respectively. In Figure 7, it is shown that, t he transient photo volta ge decay increases with magnetic field. The increase of magnetic field corresponds to low diffusion coefficient and diffusion length as demonstrated by [12]. Hence, excess minority carriers don’t cross the j unction and so me of them are d eflected lead ing to lo w transient p hoto- current delivered by the solar cell as shown by [9]. 4. Conclusions The transient photo voltage decay occurring between two steady state operating points of a solar cell under magnetic field is studied. The corresponding experimental setup is recalled and the theoretical calculations of both the transient excess minority carriers density which is the sum of an infinite terms and photo voltage decay are made. Studies of effect of the magnetic field showed that eigenvalues decreased with magnetic field, con- versely, to decay time constants which increased with mag netic field. When the magnetic field B is lower than 0.001 T, the transient excess minority carriers density is equal to the contribution of the fundamental mode. The transient photo voltage decay can be used for the determination of recombination parameters. But for magnetic field greater than 0.001 T, the excess minority carriers density is the sum of all terms and the transient decay method is not recommended for the characterization of the solar cell. References [1] Mbodji, S., Mbow, B., Barro, F.I. and Sissoko, G. (2011) A 3D Model for Thickness and Diffusion Capacitance of Emitter-Base Junction Determination in a Bifacial Polycrystalline Solar Cell under Real Operating Condition. Turkish Journal of Physics, 35, 28 1 -291. [2] Sissoko, G. and Mbodji, S. (2011) A Method to Determine the Solar Cell Resistances from Single I-V Characteristic Curve Considering the Junction Recombination Velocity (Sf) . International Journal of Pure and Applied Sciences and Technology, 6, 103-114. [3] Mbodji, S., Dieng, M., Mbow, B., Barro, F.I. and Sissoko, G. (2010) Three Dimensional Simulated Modelling of Dif- fusion Capacitance of Polycrystalline Bifacial Silicon Solar Cell. Journal of Applied Science and Technology (JAST),  S. Mbodji et al. 15, 109-114. http://dx.doi.org/10.4314/jast.v15i1-2.54834 [4] Itturri-Hinojosa, A., Resendiz, M.L. and Torchynska, T.V. (2010) Numerical Analysis of the Performance of p -i-n Di- ode Microwave Switches Based on Different Semiconductor Materials. International Journal of Pure and Applied Sciences and Technology, 1, 93-99. [5] Cuevas, A., Stocks, M., Macdonald, D. and Sinton, R. (1998) Applications of the Quasi-Steady-State-Photoconduc- tance Technique. Proceedings of 2nd World Conference and Exhibition on Photovoltaic Solar Energy Conversion, 1236-1241. [6] Rose, B.H. an d Weaver, H.T. (1983) Determination of Effective Surface R eco mbin ati on Veloci ty and Minority Carrier Lifetime in High-Efficiency Si Solar Cells. Journal of Applied Physics, 54, 238-247. http://dx.doi.org/10.1063/1.331693 [7] Bitnar, B., Glatthaar, R., Marckmann, C., Spiegel, M., Tölle, R., Fath, P., Willeke, G. and Bucher , E. (1998 ) Lifetime Investigations on Screenprinted Silicon Solar Cells. Proceedings of the 2nd World Conference and Exhibition on Photovoltaic Solar Energy Conversion, 1362-1365. [8] Barro, F.I., Mbodji, S. , Ndiaye, A.L., Zerbo, I., Madougou, S., Zougmore, F. and Sissoko, G. (2004) Bulk an d Surface Parameters Determination by a Transient Study of Bifacial Silicon Solar Cell under Constant White Bias Light. Pro- ceedings of 19th European Photovoltaic Solar Energy Conference, 262-265. [9] Mbodji, S. , Mbow, B., Dieng, M., Barro, F.I. and Sissoko, G. (2010) A 3D Model for Thickness and Diffusion Ca- pacitance of Emitter-Base Junction in a Bifacial Polycrystalline Solar Cell. Global Journal of Pure and Applied Sci- ences, 16, 469 -47 8. [10] Bocande, Y. L., Corréa, A., Gaye, I., Sow, M.L. and S is so ko, G. (199 4) Bulk and Su rfaces P aramete rs Deter minatio n in High Efficiency Si Solar Cells. Pro c eedings of the World Renewable Energy Congress, 3, 1698-1700 . [11] Lim, J., Kang, C., Kim, K., Park, I., Hwang, D. and Park, S. (2006) UV Electroluminescence Emission from ZnO Light-Emitting Diodes Grown by High-Temperature Radiofrequency Sputtering. Advanced Materials, 18, 2720-27 24 . http://dx.doi.org/10.1002/adma.200502633 [12] Diao, A., Thiam, N., Zoungrana, M., S a hi n , G., Ndiaye, M. and Sissoko, G. (2014 ) Diffusion Coefficient in Silicon Solar Cell with Applied Magnetic Field and under Frequency: Electric Equivalent Circuits. World Journal of Con- densed Matter Ph ys ics, 4, 84-92. http://dx.doi.org/10.4236/wjcmp.2014.42013 [13] Pisarkiewicz, T. (2004) Photodeacay Method in Investigation of Materials and Photovoltaic Structures. Opto-Elec- tron ics Review, 12 , 33-40. [14] Nakade, S., Kanzaki, T., Wada, Y. and Yanagida, S. (2005) Stepped Light-Induced Transi ent M easurement s of Ph oto- curren t and Vol tage in Dye-Sensitized Solar Cells: Application for Highly Viscous Electrolyte Systems. Lan g m ui r, 21, 10803-10807. [15] Schmidt, J. and Aberle, A.G. (1997) Accurate Method for the Determination of Bulk Minority-Carrier Lifetimes of Mono- and Multicrystalline Silicon Wafers. Journal of Applied Physics, 81, 61 8 6-6199. http://dx.doi.org/10.1063/1.364403 [16] Barro, F.I., Seido u Maiga, A., Wereme, A. and Sissoko, G. (2010) Determination of Recombinatio n Parameters in the Base of a Bi facial Silicon Solar Cell under Constant Multispectral Light. Physical and Chemical News, 56, 76-84. [17] Diallo, H.L., M aiga, A.S., Wereme, A. an d Sissoko, G. (2008) New Approach of both Junction and Back Surface Re- combination Velocities in a 3D Modelling Study of a Polycrystalline Silicon Solar Cell. The European Physical Jour- nal Appl ie d P hy s ic s , 42, 193-211. http://dx.doi.org/10.1051/epjap:2008085 [18] El-Adawi, M.K. and Al-Nuaim, I.A. (2002) A Method to Determine the Solar Cell Series Resistances from a Single I-V Characteristic Curve Considering Its Shunt Resistance—New Approach. Vaccum, 64 , 33-36. http://dx.doi.org/10.1016/S0042-207X(01)00370-0 [19] Zerbo, I., Zoungrana, M., Ouedraogo, A., K o r go, B., Zouma, B. and Bathiebo, D.J. (2014) Influence of Electromag- netic Waves P ro duced by an Amp lit ude M odulat ion R adi o Ant enna o n t he E lectr ic Po wer Deliver ed b y a Sil ico n S olar Cell. Global Journal of Pure and Applied Sciences, 20, 139-148. http://dx.doi.org/10.4314/gjpas.v20i2.9 [20] Madougou, S., Made, F., Boukary, M.S. and Sissoko, G. (2007) I-V Characteristics For Bifacial Silicon Solar Cell Studi ed under a Magnetic Fi eld. Advanced Materials Resea r ch, 18, 3 03 -312. http://dx.doi.org/10.4028/www.scientific.net/AMR.18-19.30 3 [21] Madougou, S., Nzonzolo, Mbod ji, S., Barro, I.F . and Si ssoko, G. (20 04) Bifacial Sil icon Solar Cell Space Ch arge Re- gion Width Determination by a Study in Modelling: Effect of the Magnetic Fiel d. Journal des Science, 4, 116-123. [22] Vardayan, R.R., Kerst, U., Wawer, P., Nell, M.N. and Wagemann, H.G. (1998) Method of Measurement of All Re- combination Parameters in the Base Region of Solar Cells. Pro ceedings of 2nd Conference and Exhibition on Photo- voltaic Solar Energy Conversion, Vienna, 6-10 July 1998, 191-193.  S. Mbodji et al. [23] Madougou, S., Made, F., Boukary, M.S. and Sissoko, G. (2007) Recombination Parameters Determination by Using Internal Quantumm Efficincy(IQE) Data of Bifacial Silicon Solar Cells. Advanced Materials Research, 18-19 , 31 3-324. http://dx.doi.org/10.4028/www.scientific.net/AMR.18-19.31 3 [24] Goyal, M. (2007) Computer-Based Numerical & Statistical Techniques . Infinity Science Press, LLC, Hingham.
|