World Journal of Engineering and Technology
Vol.03 No.03(2015), Article ID:61139,6 pages
10.4236/wjet.2015.33C054
GDOP’s Influence on Observable Degree of Multi-Antenna GPS/SINS Integrated Attitude Measuring System
Hao He, Yuhang Zheng, Dongfang Yang, Jinsheng Zhang, Shicheng Wang
Xi’an High-Tech Institution, Xi’an, China
Email: hehao209@126.com


Received 8 October 2015; accepted 23 October 2015; published 30 October 2015

ABSTRACT
GDOP’s influence on observable degree is studied by analyzing a multi-antenna GPS/SINS attitude measuring system. Firstly, the mathematical model of the attitude measuring system, whose observations are single-differences, is provided; Secondly, it is proved that the model can be studied by PWCS theory, and GDOP’s influence on observable degree is explained intuitively. Then, the variance of observable degree is studied by simulation while GDOP is different, and the result is analysed. Simulation results show that, the observable degree becomes worse with the increasing GDOP value. Therefore, while designing such kind of Kalman filter, the influence to observable degree which made by GDOP should be considered adequately.
Keywords:
Attitude Measuring, Observable Degree, SVD, GDOP

1. Introduction
A multi-antenna GPS/SINS attitude measuring system,whose observe vectors are single-differences, is established. Those observe including baseline vector, velocity and position. By such system, the error which cause by signal delay is decreased. While designing such a Kalman Filter, the observability of states should be considered. Usually, it can be analysed by PWCS theory [1] [2]. PWCS solves the problem of whether the states can be observed totally. In order to analyze the observability in quantification, the concept of observable degree [3] is introduced. And the method of singular value decomposition (SVD) is in common use. However, SVD is not perfect, for the dimensions of states are not the same, and the singulars in different order of magnitudes reflect no more than a compare. It means, at the same system, the more the singulars in the same order is, the more the observable degree is.
Reference [3] analyzes the observability strapdown inertial navigation system by SVD, and points out that, SVD is adapted to system state estimation of time-varying dynamic systems. References [4]-[6] analyze the observability of loose-coupled, tightly-coupled and ultra-tight coupled model of GPS/INS. These references prove that, the GPS/INS integrated systems meet the requirement of PWCS, and analyze their observability in different motions. Reference [7] compares the observable degree of GPS/SINS complete integrated system (CIS) and tightly coupled system (TIS) with different number of visible stars, points out that CIS is better in observable degree than TIS, and as the same system, increasing number of visible stars makes the observable degree raising.
How about it while the number of visible stars is the same but geometric dilution of precision (GDOP) is not? Generally speaking, GDOP affects the precision of GPS receiver and still the integrated system. But no reference shows how it affects the observable degree of GPS/SINS integrated system. By analyzing a GPS/SINS integrated attitude measuring system, which is another type of CIS, the GDOP’s influence to the observable degree is studied.
2. Mathematical Model of GPS/SINS Integrated Attitude Measuring System
2.1. Error Equation of SINS
Error equation of Mathematics Platform,
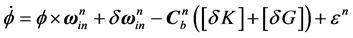 (1)
(1)
Error equation of velocity,
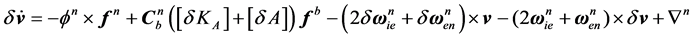 (2)
(2)
Error equation of position,
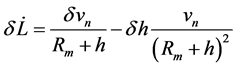 (3)
(3)
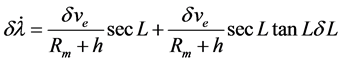 (4)
(4)
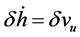 (5)
(5)
2.2. The State Space Equation
The GPS/SINS integrated system state space equation is established by error of SINS parameters.
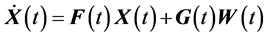 (6)
(6)
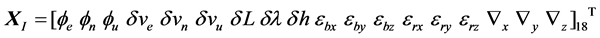 (7)
(7)
In Equation (7),  are alignment errors of Mathematics Platform;
are alignment errors of Mathematics Platform; 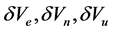 are velocity errors of SINS;
are velocity errors of SINS; 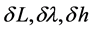 are latitude, longitude and altitude errors of SINS,
are latitude, longitude and altitude errors of SINS, 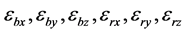 are constant drift errors and correlated drift errors of gyro.
are constant drift errors and correlated drift errors of gyro. 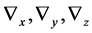 are equivalent errors of accelerometer.
are equivalent errors of accelerometer.
State-transition matrix is
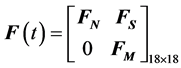 (8)
(8)
In Equation (8), 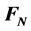 is a transition matrix corresponding 9 parameters error of SINS.
is a transition matrix corresponding 9 parameters error of SINS.
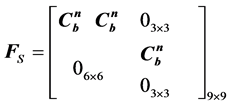 (9)
(9)
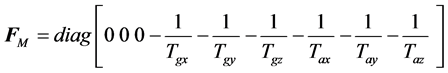 (10)
(10)
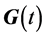 is the allocation matrix of noise,
is the allocation matrix of noise, 
2.3. The Measurement Equation
The attitude measuring part of system is realized by GPS multi-antenna layout and carrier phase relative positioning technique. Figure 1 shows a typical layout of multi-antenna GPS.
Calculate the double difference of GPS measurements, attitude measurement equations can be obtained as,

While, 



Pseudo-range observations based on single-difference equation:

Doppler velocity measurement based on single-difference equation:

where, 
Make the system measurements to be

Therefore, the observation equation is

where,




Figure 1. A layout of multi-antenna.
3. Observability Analysis
The model established before is a time-varying one. It should be analyzed by PWCS, before which, the model can be studied by PCWS needs to be proven.
It is proved that the model multi-antenna GPS/SINS integrated system accord with the PWCS theorem.


According to the definition of observability analysis matrix,

Elementary row transformation to

Set

In Equation (30), 
Therefore, 




4. GDOP’s Influence on Observable Degree
4.1. Intuitive Interpretation
Analyzes the observability by PWCS method, and results show that the rank n = 18 while the N Asset Coverage is 4, which means all the state are observable. It is obvious that the observability of states will be different while the GDOP is different. AS baseline vector B.
Figure 2 shows that, as measurements, 

Figure 2. Projection of baseline B on vector S.


Similar, the velocity and position part have the same conclusion. While the transition matrix F is the same, GDOP affect the observation equation H, and better GDOP makes better H.
PWCS theory does not show the difference when GDOP is different. Therefore, quantitative analysis is needed to study the observability degree. SVD is a common method to analyze the observable degree. But SVD is still defective because of the different dimension of states. So analyzes the observable degree changes of system-level only when GDOP changes.
4.2. Simulation Analysis
Simulation based on a 1000 sec long track, analyze the observable degree while GDOP changes. Set the N Asset Coverage 4, the length of baseline in Y axis 10 m, in X axis 5 m. Angle heading


Choose satellites number as 4, 13, 16, 19, and the averaged GDOP during simulation is 3.4; Choose satellites with number 4, 18, 19, 21, and the averaged GDOP during simulation is 12.3; Table 1 shows the SVD to SOM of simulations. The results shows that all 18 states are observable, and corresponding states are almost in the magnitude. While GDOP = 3.4, 




5. Conclusions
A GPS/SINS integrated attitude measuring system is established, and proof of it can be studied by PWCS theory is given. By using SVD and condition number method, how GDOP affects the observable degree of integrated is studied. Conclusions are obtained:
1) The integrated system this paper introduced can be studied by PWCS theory, and all its states are observable while the N Asset Coverage is more 4.
2) The relationship between GDOP and measurement matrix is studied. The less the GDOP is, the more significant the measurement matrix is. And still the precision become better.
3) The relationship between GDOP and system-level observable degree is studied via SVD and condition. The result shows that observable degree becomes worse with the increase of GDOP.
Table 1. The observable degree of different GDOPs.
Meanwhile, the conclusion comes from a certain model of GPS/SINS, of which the measurements are single- differences and double-differences. Further research is needed, for whether the conclusion is also correct for other models.
Cite this paper
Hao He,Yuhang Zheng,Dongfang Yang,Jinsheng Zhang,Shicheng Wang, (2015) GDOP’s Influence on Observable Degree of Multi-Antenna GPS/SINS Integrated Attitude Measuring System. World Journal of Engineering and Technology,03,354-359. doi: 10.4236/wjet.2015.33C054
References
- 1. Goshen-Meskin, D. and Bar-Itzhack, I.Y. (1992) Observability Analysis of Piece-Wise Constant Systems (Part I): Theory. IEEE Transactions on Aerospace and Electronic Systems, 28, 1056-1106. http://dx.doi.org/10.1109/7.165367
- 2. Goshen-Meskin, D. and Bar-Itzhack, I.Y. (1992) Observability Analysis of Piece-Wise Constant Systems (Part II): Application to Inertial Navigation In-Flight Alignment. IEEE Transactions on Aerospace and Electronic Systems, 28, 1068-1075. http://dx.doi.org/10.1109/7.165368
- 3. Cheng, X.H., Wan, D.J. and Zhong, X. (1997) Study on Observability and Its Degree of Strapdown Inertial Navigation System. Journal of Southeast University, 27, 6-10.
- 4. Shuai, P., Chen, D.C. and Jiang, Y. (2004) Observable Degree Analysis Method of Integrated GPS/SINS Navigation system. Journal of Astronautics, 25, 219-224.
- 5. Liu, F., Hu, X.M., Weng, H.N., et al. (2011) Observbility Analysis of SINS/GPS Tightly Coupled System. Journal of Tianjin University, 44, 391-395.
- 6. Zhou, W.D., Cai, J.N., Sun, L., et al. (2013) Observability Analysis of GPS/SINS Ultra-Tightly Coupled System. Journal of Beijing University of Aeronautics and Astronautics, 39, 1157-1162.
- 7. Hu, X.M., Liu, F. and Weng, H.N. (2011) Observability Analysis of MSINS/SINS Complete Integrated System. Journal of Chinese Inertial Technology, 19, 38-45.
- 8. Ma, Y.H. and Hu, J. (2008) Counterexamples for Degree of Observability Analysis Method Based on SVD Theory. Journal of Chinese Inertial Technology, 16, 448-452.




