Received 3 October 2015; accepted 23 October 2015; published 30 October 2015

ABSTRACT

The paper presents the prerequisites of involving of topological elements and graph theory as an instrument of mathematical formalization of woven structures and technology of textile fabrics. Present research is based on analysis and comparison of the main concepts and conditions of textile technology and graph theory.

Keywords:

Textile, Weaving, Structure, Plain Weave, Twill Weave, Rapport, Topology, Graph Theory, Vertex, Valency, Edge, Warp, Weft

Topology as a chapter of geometry has a lot in common with one of the branches of mathematics―the graph theory, which starts from the solving of task about Seven Bridges of Koennigsberg by Leonhard Euler. Efforts to attract the arsenal of this theory to the technological challenges of weaving are applied to determine the possi- bility of developing a predetermined color pattern with single-layer weave. But the data of the task “... to the coloring of a vertex of given color pattern’s structure in two colors that denote zero and one, ...” does not allow to bring the solution of the technological problem to describe the topology of the warp and weft of the whole field of weaving rapport considering full spatial orientation, and moreover, to obtain a specific numerical characteristics of the factor of weave.

The closest familiarization with the elements of this theory convinces us that more productive methods of application of graph theory to the problem of structural analysis of the weave of fabrics are available. To this end, we present some basic concepts and definitions of graph theory needed to solve our problems.

Graph, denoted as G = (V, E), consists of two types of elements called vertices and edges, respectively. Each edge has two vertices, and they usually indicated as υ₁, υ₂, υ₃, …, and edges-e₁, e₂, e₃, …. Vertices υ_i and υ_j, identifying edge e_l, called end vertices of edge e_l. Edge e_l is denoted by e_l = (υ_i, υ_j).

Graph G is called directed or oriented, if its edges are defined as an ordered pair of end vertices. All edges with equal end vertices are parallel. An edge whose endpoints are the same vertex is called a loop.

A graph is a simple graph if it has no multiple edges and loops. An empty graph is a graph with no edges. A graph with no vertices and edges is called null graph.

Graphical presentation of a graph is a diagram, on which a vertex is displayed as a dot, and an edge as a piece of line connecting dots, which match end vertices of an edge. For example, if V = {υ₁, υ₂, υ₃, υ₄, υ₅, υ₆} and E = {e₁, e₂, e₃, e₄, e₅} so, that e₁ = (υ₁, υ₂), e₂ = (υ₁, υ₄), e₃ = (υ₅, υ₆), e₄ = (υ₁, υ₂), e₅ = (υ₅, υ₅), then G = (V, E) is the same as in Figure 1. In this graph, e₁ and e₄ are parallel edges, and e₅ is a loop. Two vertices are called adjacent if an edge exists between them. Two edges are called adjacent if a vertex exists between them.

The edge e₁ of the graph, which is shown in Figure 1, is incident to vertices υ₁ and υ₂; υ₁ and υ₄ are adjacent vertices, and e₁ and e₂ are adjacent edges. The number of incident edges to vertex υ_i is called the degree, or valency of the vertex, and is labeled d(υ_i). A vertex of degree 1 is a leaf. A vertex of degree 0 is an isolated vertex. The maximum degree Δ(G) of a graph G is the largest degree over all vertices, the minimum degree δ(G), the smallest. In Figure 1 for graph G:

υ₃―an isolated vertex, υ₄ и υ₆―pendant vertices, e₂―a pendant edge. The sum of the degrees of vertices is 10, quantity of edges―5. So, the sum of the degrees of vertices is equal to doubled number of edges, and therefore is an even integer. Moreover, the number of vertices of graph G in odd degree is also an even integer. This is right for any graphs.

Let’s describe the structure of a weave using a graph. As a minimal part of fabric we examine the rapport of weave. The rapport of a random weave for any R_o, R_y ≥ 2, at optional R_o = R_y, in categories of graph theory represents a simple and undirected graph with order n = R_o × R_y. Let’s call it a structural graph of fabric. In structural graph of fabric, the appearance of loops in categories of graph theory is not allowed, technologically it is a defect.

Weaving cover in a range of rapport matches vertices, and the lines of warp and weft match edges of a graph. But in general, during considering of woven structure as an unlimited field with sequentially located rapports in direction of warp and weft, the valency of random vertex of a graph d(υ_i) = 4, but at separate examination of weaving rapport, the valency has an integer value from 2 to 4.

Figure 2 presents the simplest example of the graph of plain weave. It represents a simple undirected graph G = (V, E) of an order: n = R_o × R_y = 2 × 2 = 4 with V = {υ₁, υ₂, υ₃, υ₄} and E = {e₁, e₂, e₃, e₄}, where e₁ = (υ₁, υ₂), e₂ = (υ₁, υ₃), e₃ = (υ₂, υ₄) and e₄ = (υ₃, υ₄). The graph has following pairs of adjacent vertices: υ₁ and υ₂; υ₁ and υ₃; υ₂ and υ₄; υ₃ and υ₄, and following pairs of adjacent edges: e₁ and e₂; e₁ and e₃; e₂ and e₄; e₃ and e₄. Edges e₁, e₂, e₃ and e₄ are incident to their end vertices υ₁ and υ₂; υ₁ and υ₃; υ₂ and υ₄; υ₃ and υ₄ respectively.

The valency of all four vertices of graph, at separate examination of the rapport of weave irrelatively with separate rapports in direction of warp and weft in unlimited field of rapports in fabric structure equals:

The sum of degrees of vertices:

Therefore, the equality rule of the sum of degrees of vertices to doubled number of its edges is right for the graph, because the number of its edges is equal to 4 [1].

One more example is twill 1/2 weave (Figure 3). Graph G = (V, E) of this weave is a simple undirected graph

and consists of two multiplicities: vertices υ₁, υ₂, υ₃, υ₄, υ₅, υ₆, υ₇, υ₈, υ₉ and edges e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂. It has following pairs of adjacent vertices υ₁ and υ₂; υ₂ and υ₃; υ₁ and υ₄; υ₂ and υ₅; υ₃ and υ₆; υ₄ and υ₅; υ₅ and υ₆; υ₄ and υ₇; υ₅ and υ₈; υ₆ and υ₉; υ₇ and υ₈; υ₈ and υ₉, which are the end points of edges e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂ respectively, and following pairs of adjacent edges: e₁ and e₂; e₁ and e₃; e₁ and e₄; e₂ and e₅; e₃ and e₆; e₄ and e₆; e₄ and e₇; e₅ and e₇; e₆ and e₈; e₆ and e₉; e₇ and e₉; e₇ and e₁₀; e₈ and e₁₁; e₉ and e₁₁; e₉ and e₁₂; e₁₀ and e₁₂. Comparing to the previous graph of plain weave, the valency of edges is different, and adopts values 2 and 4. Namely, d(υ₁) = 2, d(υ₂) = 3, d(υ₃) = 2, d(υ₄) = 3, d(υ₅) = 4, d(υ₆) = 3, d(υ₇) = 2, d(υ₈) = 3, d(υ₉) = 2.

The sum of degrees of edges:

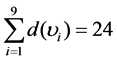
The number of egdes is 12. Therefore, in this case doubled number of edges gives the sum of valencies of edges, i.e.

And the order of graph equals: n = R_o × R_y = 3 × 3 = 9.

On the basis of two simple examples of graphs of plain and twill weaves, it is possible to make some abstractions. Particularly, for the sum of valencies of edges.

In any graph of weave, an existence of four vertices, whose valency equals two is inherent. In plain weave, these four vertices with degree of 2 is the set of vertices existing in a graph. But in general, with random R_o and R_y, the number of these vertices from a multiplicity of all vertices equals 4. In total sum of degrees of vertices, these 4 vertices give 4 × 2 = 8 valencies. There are also vertices with valency of 3 exist in the graph of weave, located “on the perimeter” of rapport, except angular as, for example, vertices υ₂, υ₄, υ₆, and υ₈ of twill weave 1/2. And finally, in general case of the graph of weave there are vertices with the valency of 4, located “inside” the rapport, such as vertex υ₅ of the graph of twill 1/2 in Figure 3.

Therefore, the sum of valencies of all vertices of fabric’s structural graph of a random weave will be:

Required dependence to define the sum of valencies of vertices, comparable to any rapport of weave at random values R_о и R_у:

The number of the edges of weave equals: 2R_оR_у-R_о-R_у.

And it is obvious that the structural graph of fabric with random weave can be presented as a cycle. Specifically, in case of plain weave with R_о = R_у = 2, it presents a cycle as a sequence υ₁, е₁, υ₂, е₃, υ₄, е₄, υ₃, е₂, υ₁. It is the simplest case with minimum number of cycles, 1. Then, as rapport increases, also the number of cycles increases. In case of twill 1/2 with R_о = R_у = 3, already four cycles are appearing: 1) υ₁, е₁, υ₂, е₄, υ₅, е₆, υ₄, е₃, υ₁; 2) υ₂, е₂, υ₃, е₅, υ₆, е₇, υ₅, е₄, υ₂; 3) υ₄, е₆, υ₅, е₉, υ₈, е₁₁, υ₇, е₈, υ₄; 4) υ₅, е₇, υ₆, е₁₀, υ₉, е₁₂, υ₈, е₉, υ₅ [1].

Cite this paper

Otabek Kasimov, (2015) Basic Concepts of Graph Theory as the Instruments of Mathematical Formalization of Woven Structures. World Journal of Engineering and Technology,03,344-347. doi: 10.4236/wjet.2015.33C052

References