Applied Mathematics, 2015, 6, 1957-1967
Published Online November 2015 in SciRes. http://www.scirp.org/journal/am
http://dx.doi.org/10.4236/am.2015.612173
How to cite this paper: Al Qarni, A.A., Banaja, M.A. and Bakodah, H.O. (2015) Numerical Analyses Optical Solitons in Dual
Core Couplers with Kerr Law Nonlinearity. Applied Mathematics, 6, 1957-1967. http://dx.doi.org/10.4236/am.2015.612173
Numerical Analyses Optical Solitons in Dual
Core Couplers with Kerr Law Nonlinearity
A. A. Al Qarni1, M. A. Banaja2, H. O. Bakodah2
1Department of Mathematics, Faculty of Science for Girls, Bisha University, Bi sha , Saudi Arabia
2Department of Mathematics, Faculty of Science for Girls, King Abdulaziz University, Jeddah, Saudi Arabia
Received 27 May 2015; accepted 6 November 2015; published 9 November 2015
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Abstract
In this paper, we present the results of numerical analysis of optical solitons in dual core couplers.
We studied the optical couplers as an application for the non-linear Schrödinger equation in the
case of Kerr law for non-linear and clarify the exact solution in this case. Then we have provided a
numerical study of the effect of changing the constants in the form of the three types of s ol iton s:
bright soliton and dark solitons and singular soliton.
Keywords
Optical Soliton, Dual Core Couplers, Kerr Law Nonlinearity
1. Introduction
The propagation solitons through optical fibers have been a major area of study given its potential applicability
in optical co mmunication syste ms. Several effects that are present in optical fibers and ampli fiers limit the per-
formance of optical system. Signal propagation through optical fibers can be affected by group velocity disper-
sion (GVD), polarization mode dispersion (PMD), and nonlinear effects. The main nonlinear effects that arise in
monomode fibers are Brillion scattering, Raman scattering, and the Kerr effect. The Kerr effect of nonlinearity
is due to the dependence of the fiber refractive index on the field intensity. The intensity dependence of the re-
fractive index leads to a larger number of interesting nonlinear effects. Notable among them, which have been
studied widely, are self-phase modulation (SPM) and cross phase modulation (XPM). The propagation solitons
through optical fibers have been well established that this dynamics is described, to first approximation, by the
integral nonlinear Schrodinge r equation (NLSE) [1]. The N onlinea r Schr odin ger’s Eq uation plays a vital ro le in
various areas of physical, biological, and engineering sciences. It appears in many applied fields, including fluid
dyna mi c s, nonlinear optics, plasma physics, and protein chemistry. The NLSE that is going to be studied is giv-

A. A. Al Qarni et al.
1958
en by
( )
2
10
2
t xx
iqqF qq++ =
(1)
F is a real-valued algebraic function, q is the dependent variable, x and t are the independent variables.
Equation (1) is known to support solitons or soliton solutions for various kinds of nonlinearity.
There are various kind s of nonli nearit i es o f the function F in ( 1) tha t are known so far.
The special case where
( )
Fs s=
, also known as the kerr law of nonline arit y, is i ntegr able b y the metho d of
inverse scattering transform (IST) [2 ]-[5].
The Kerr law of nonlinearit y originates from the fact that a light wave in an o ptical fiber faces nonlinear res-
ponses from nonharmonic motion of electrons bound in molecules, caused by an external electric field. Even
though the nonlinear responses are extremely wea k, their effects appear in vario us ways over long distances of
propagation that are measured i n ter ms of light wavelength.
2. Dual -Core Couplers
Nonlinear couplers are very useful devices that distribute light from a main fiber into one or more branch fibers.
Couplers also have applications as intensity dependent switches and as limiters.
Switching is the process of energy redistribution between the cores for a given input. The problem of switch-
ing, although involved, can be accomplished when the stability of soliton states is known.
Although there has been a lot of work in the area of optical couplers, our approach in this paper is going to
present the special cases of the kerr-law no nli ne ar ity.
Also, t he r e has been a lot of exact and approximate numerical studies in the context of optical couplers. But
these numerical techniques could get computatio nall y intense [6] [7].
For Dua l-core couplers, wave p ro pagatio n at relativel y high field in tensitie s is descr ibed by co upled nonlinear
equa tions. In the dime nsionl ess form, they are
( )
2
11 1t xx
iqa qbFqqKr++ =
(2)
( )
2
22 2t xx
ira rb FrrKq++ =
(3)
Equa t ions (2) and (3) represent a generic model to study the dynamics of optical solitons through dual-core
optical couplers.
The first term in both equations represent linear temporal evolution. The coefficients of
l
a
for
1, 2l=
is
the group velocity dispersion (GVD) while
l
b
represent non-Kerr law nonlinearity, in general. On the right
hand sides
l
K
are the coupling coefficients. The dependent variables
( )
,q xt
and
( )
, r xt
are the com-
plex-valued wave profiles that propagate through these couplers. In this research, the focus is limited to soliton
signals.
The functional F represents non-Ke rr law nonlinearity, i n general.
For Kerr l aw nonli nearity,
( )
Fs s=
. The model Equations (2) and (3) reduces to
2
11t xx
iqaqbqqK r++ =
(4)
2
22t xx
irarbrrKq++ =
(5)
For integrality aspects of this coupled equations by ansatz method an assumption of the following form is
considered:
() ()
()
,
1
, ,e
i xt
q xtPxt
φ
=
(6)
( )( )
()
,
2
, ,e
i xt
r xtPxt
φ
=
(7)
where
() ()
,1; 2
l
P xtl=
represents the amplitude components of soliton while the phase component
( )
,xt φ
is
( )
,x tkxt φ ωθ =−+ +
(8)

A. A. Al Qarni et al.
1959
In (6), K is the frequency of t he solution ’s while ω represents the wave number and
θ
is the phase consta nt.
Substituting (6) and (7) into (4) and (5) and then decomposi ng into real and imaginary parts give
( )
( )
22
2
2
0
l
llll lll
l
P
aPakbF PPKP
x
ω
∂−+ +−=
∂

(9)
and
20
ll
l
PP
ak
tx
∂∂
−=
∂∂
(10)
Respectively.
From the imaginary part equation it is possible to obtain the speed (v) of the soliton as,
2l v aK= −
(11)
Since
()
,
l
P xt
can be represented as
( )
l
P xvt−
, where the function g is the soliton wave profile depending
the type of nonlinearity and v is the speed of the soliton.
Now, equating the two values of the soliton speed, from (11) leads to
12
aa=
(12)
The speed of the soliton therefore red uces to
2v aK= −
(13)
The coupled NLSE for dual-core couplers given by (4) and (5) modifies to
( )
2
11 1t xx
iqa qb FqqKr++ =
(14)
( )
2
22 2t xx
ira rb FrrKq++ =
(15)
where
12
aaa= =
Consequently, the real part Equation (9) reduces to
( )
22
2
3
0
lllll
l
l
P
aPakbP KP
x
ω
∂− ++−=
∂


(16)
This equation will no w be integrated for three typ es of solit ons. The y are bright, da rk and sing ular solito n so-
lutions.
3. Families of Soliton Solutions
3.1. Bright Solitons
For bright solitons, one assumes [8] [9]
sech ;
l
P
ll
PA τ =
(17)
where;
( )
–Bxvt τ =
(18)
Here,
l
A
represents the soliton a mplitud e a nd
B
is the inverse width of the soliton.
Substitutin g (17) into (16) gives:
( )
( )
( )
2 2 222
3 3
sech1 sech
sechsech 0
ll
l
l
pp
llll l
P
p
ll l
l
AakapBaAp Bp
b AKA
ωτ
ττ
+
+−+ +
− +=


(19 )
Balancing pr inciple yields
23
ll
pp+=
(20)
So that
1 for1,2.
l
pl= =
(21)

A. A. Al Qarni et al.
1960
Substituting (21) into (19) we get:
() ()
222 33
sech2sechsech 0
ll llll
AakaBaA BbAKA ω τττ +−+ −+=

(22)
From coefficient
sech τ
into (22) we get
22
0
l
ll
A
akaBK A ω +−+ =

and therefore:
()
22 l
ll
A
aB kKA ω = −−

(23)
From coefficient
3
sech , τ
we get
2 2
20
l
aA Bb−=
and therefore:
2
ll
b
BA
a
=
(24)
which poses the constraint
0 for1,2.
l
ab l>=
(25)
Thi s means that the GVD and Kerr law nonl inearity must bear the sa me sign for b right so litons to exist.
Next, equating the width of the solitons for
1; 2l=
from (24) imply
22
1122
bA bA=
And therefore:
12
21
Ab
Ab
=
( 26)
whi ch again shows the
12
0bb >
(27)
This shows that the nonlinearity of the two cores must also carry the same sign. Then, equating the wave
numbers for the two components gives the relation (23) we get
22
12 21
KA KA=
and therefore:
11
22
AK
AK
=
(28 )
which again shows that
12 0
KK >
(29 )
Finally eq uating (26) a nd (28) leads to
1122
bK bK=
(30)
whic h is the co nstrai nt condi tion b etween t he give n coef ficients that must hol d for b right so litons t o exist. This
leads to the br ight 1-soliton so lutio n for dual coupler s:
( )()
( )
1
, seche
i kxt
qx tABxvt
ωθ −++
= − 

(31)
( )()
( )
2
,sech ?
i kxt
rxtABxvt
ωθ −++
=

(32)
which will exist fo r the necessary constra ints in place.
3.2. Dark Solitons
For dark solitons, the starting hypothesis is given by [6]
tanh
l
p
ll
PA τ =
(33)
with the definition of
τ
being the same in (18). However for dark solitons the parameters
l
A
and B are free
parameters. Substituting (33) and (18) into (16) leads to
( )
( )
( )
2 2 222
23
23
2tanh1 tanh
1 tanhtanhtanh0
ll
l
ll
pP
lll ll
p
pp
ll lllll
AakapBaABpp
aApB pbAKA
ωτ τ
τττ
−
+
++
=
−−
−+− +


(34)

A. A. Al Qarni et al.
1961
Balancing pr inciple yields
23
ll
pp+=
(35)
So that
1 for1,2.
l
pl= =
(36)
Substituting (36) into (34) we get:
() ()
222 33
tanh2tanhtanh 0
ll llll
AakaBaA BbAKA ω τττ +−+−+=

(37)
From coefficient
1
tanh τ
we get
22
0
l
l
A
ak aBA ω + −+=

and therefore:
( )
22 l
ll
A
aB kKA ω = −−

(38)
From coefficient
3
tanh τ
we get
2 2
20
l
aA Bb−=
and therefore:
2
ll
b
BA
a
=
(39)
which poses the constraint
0 for1,2.
l
ab l>=
(40)
Thi s means that the GVD and Kerr law nonl inearity must bear the sa me sign for b right so litons to exist.
Next, equating the width of the solitons for
1; 2l=
from (39) implied
22
1122
bA bA=
and there fore:
12
21
Ab
Ab
=
(41)
which again shows that
12
0bb >
(42)
This shows that the nonlinearity of the two cores must also carry the same sign. Then, equating the wave
numbers for the two components gives the relation (38) we get
22
12 21
KA KA=
And therefore:
11
22
AK
AK
=
(43)
which again shows that
12
0KK >
(44)
Finally equating (41) and (43) leads to
1122
bK bK=
(45)
Thi s gives dark 1 -soliton solution for dual-core couplers
( )()
( )
1
, tanhe
i kxt
qx tABxvt
ωθ
−++
= − 

(46)
( )()
( )
2
, tanhe
i kxt
rxtABxvt
ωθ −++
= − 

(47)
along with their respective constraints as indicated.
Note: These waves known as check waves.
3.3. Singular Solitons
For singular solitons, the s t arting hypothe sis is given by [6]

A. A. Al Qarni et al.
1962
csch l
P
ll
PA τ =
(48)
where
τ
is the same as in (18) while the parameters
l
A
and B are again free parameters. Upon substituting
(48) and (16) into (18) gives
( )
( )
23 2 2223
1 cschcschcsch0
l ll
p pp
lllllllll
AakapBaA BppbAKA ω τττ
+
+− −+−+=

(49)
Balancing pr inciple yields
23
ll
pp+=
(50)
So that
1 for1,2.
l
pl= =
(51)
Substituting (51) into (49) we get:
() ()
222 33
csch2cschcsch 0
ll llll
AakaBaA BbAKA ω τττ +−+ −+=

(52 )
From coefficient
csch τ
we get
22
0
l
ll
A
akaBK A ω +−+ =

and therefore:
( )
22 l
ll
A
aB kKA ω = −−

(53)
From coefficient
3
csch τ
we get
22
20
l
aA Bb−=
and therefore:
2
ll
b
BA
a
=
(54)
which poses the constraint
0 for1,2.
l
ab l>=
(55)
Thi s means that the GVD and Kerr law nonl inearity must bear the sa me sign for b right so litons to exist.
Next, equating the width of the solitons for
1; 2l=
from (54) implied
22
1122
.bA bA=
And therefore:
12
21
Ab
Ab
=
(56)
which again shows the
12
0bb >
(57)
This shows that the nonlinearity of the two cores must also carry the same sign. Then, equating the wave
numbers for the two components gives the relation (53) we get
22
12 21
.KA KA=
And therefore:
11
22
AK
AK
=
(58)
which again shows that
12 0KK >
(59)
Finally equating (56) and (58) leads to
1122
bK bK=
(60)
These lead to singular 1-soliton solutions in dual-core optical fibers with Kerr nonline arity given by
( )()
( )
1
, csche
i Kxt
qx tABxvt
ωθ
− ++
= − 

(61)
( )()
( )
2
, csche
i Kxt
rxtABxvt
ωθ − ++
= − 

(62)
which will exist fo r the necessary constra ints in place.

A. A. Al Qarni et al.
1963
4. Results of Numerical Analyses
Analytic process of the CNLS can only be found under certain special selections of parameters, i.e. certain un-
derlying physical system. For other cases, numerical analysis is necessary for seeking the evolution o f solutions.
It is essential to select a suitable numeric al method for solving the equations [10].
To study the effect of paramet er s on Solitons we conside r the following values [11]:
Case 1: if they
1
12 12
22
16
,,1.0103,,2,
2
A
bKAAv ak
bb
===== −
2
12
1, 1,6,3,,π
22
b
a kKBA
a
ωθ ======
Studying the ef fect of cha nging
2
b
(non-linear coefficient) in terms of
1
b
so take three cases
212 121
11
4,,0bbb bbb== =
Figures 1-3 shows the e ffect of this cha nge on S oliton amp litude.
Case 2: if they
1
12 12
22
16
,,1.0103,,2,
2
A
bKAAv ak
bb
===== −
2
21 12
1, 1,6,3,,π
42
b
b bkKBA
a
ωθ ==== ==
Studying the ef fect of cha nging a (velocity dispersion coefficient) on the wave form and the values
1, 1,2
2
a aa== =
Figure 4-6 shows t he effect of this change on the width Soli ton .
Case 3: if they
1
12 2
22
1 61
,,,, 2,
22
A
bKaAv ak
bb
===== −
2
21 12
1, 1,6,3,,π
42
b
b bkKBA
a
ωθ ==== ==
Studying the ef fect of cha nging
1
A
(So liton amplitude) on the wave form, and that the values of
1 11
0.550515, 1.0103,2.20206A AA== =
Figures 7-9 shows the effect of this change on the Soliton width and Soliton amplit ude.
5. Conclusions
The study couplers dual core is considered one of modern topics of great importance in the field of optical
communication. In this research, the Schrodinger equation is linear been studying these couplers in the case of
kerr law no nlinearit y and clarifying t he exact solution in this case.
An d we studied the effect of changing constants derived under the restrictions mentioned on Soliton form in
the case of Solitons bright as in the case of a change b2 (non-linear coefficient) impact on soliton amplitude.
When yo u c ha n ged a (velocity dispersion coefficient), we f ound tha t the ef fect on Soli to n width as well as when
changing
1
A
(Soliton amplitude), the i mpact o n the Soliton width and Soliton amp litude.
Similarly, these changes have in the case of dark Solito ns an d singular Solitons.
The extension of this work can apply different types of non-linear as well as increase the Perturbation terms to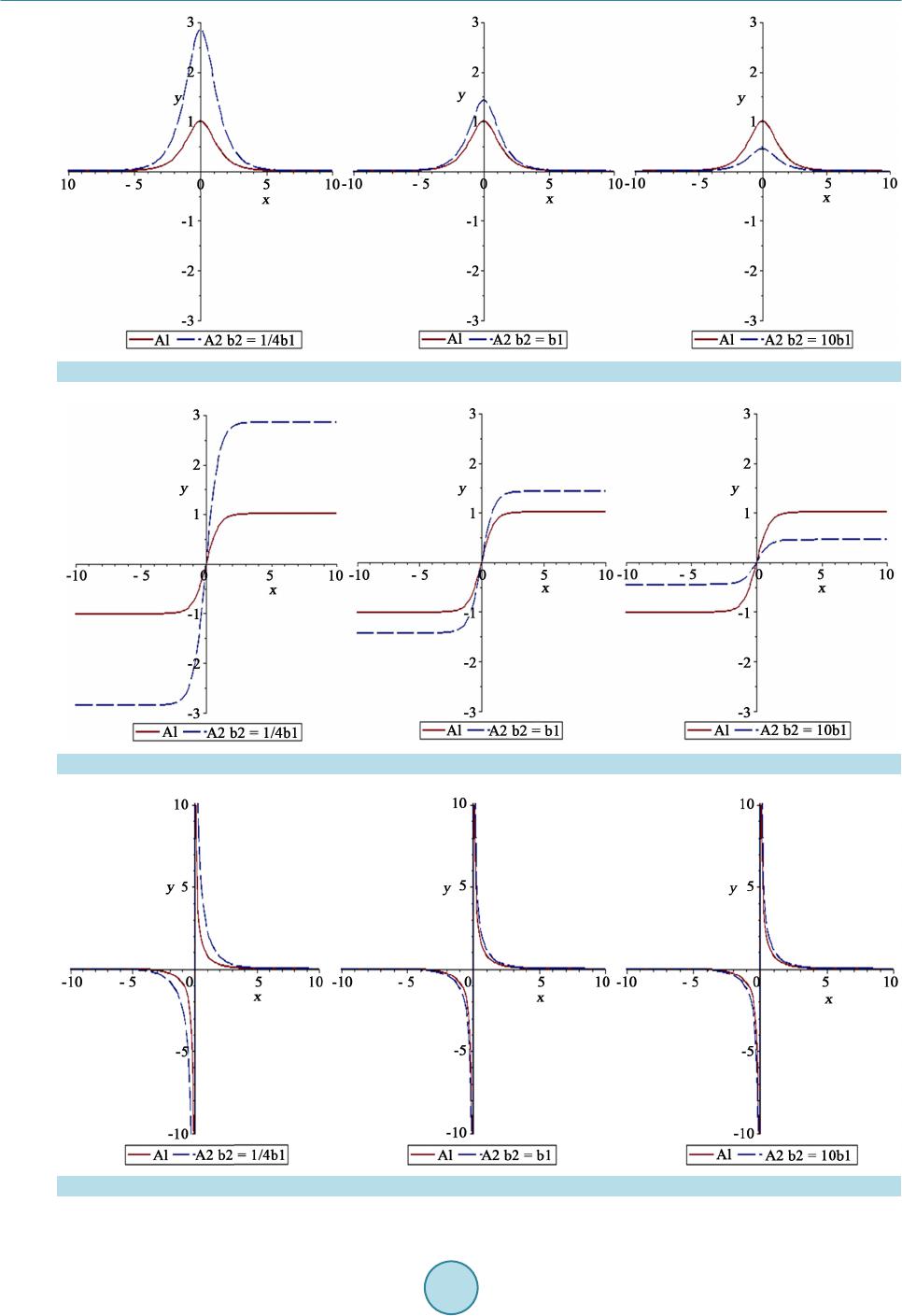

A. A. Al Qarni et al.
1964
Figure 1 . Bright solitons.
Figure 2 . Dark solitons.
Figure 3 . Singular solitons.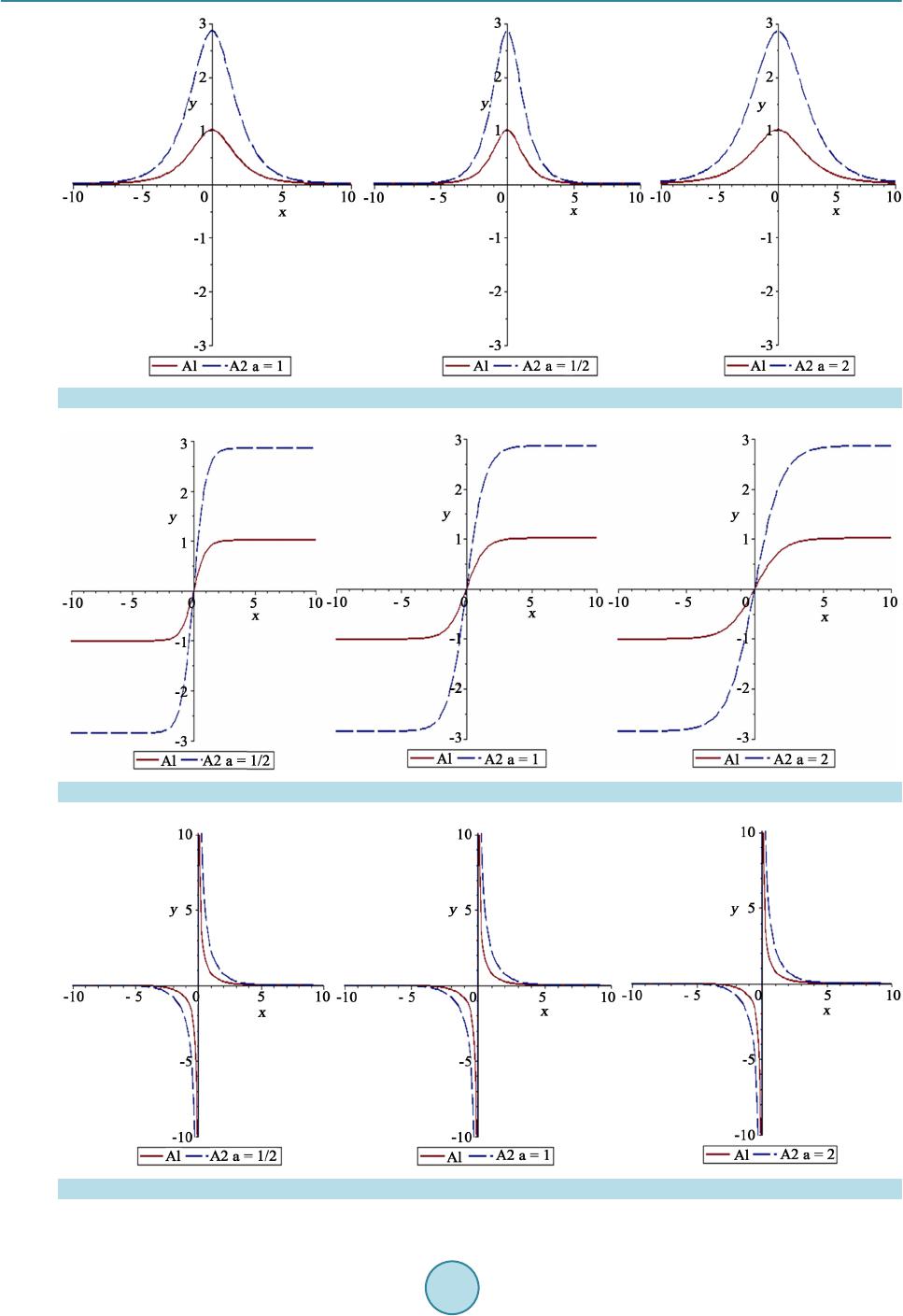

A. A. Al Qarni et al.
1965
Figure 4 . Bright solitons.
Figure 5 . Dark solitons.
Figure 6 . Singular solitons.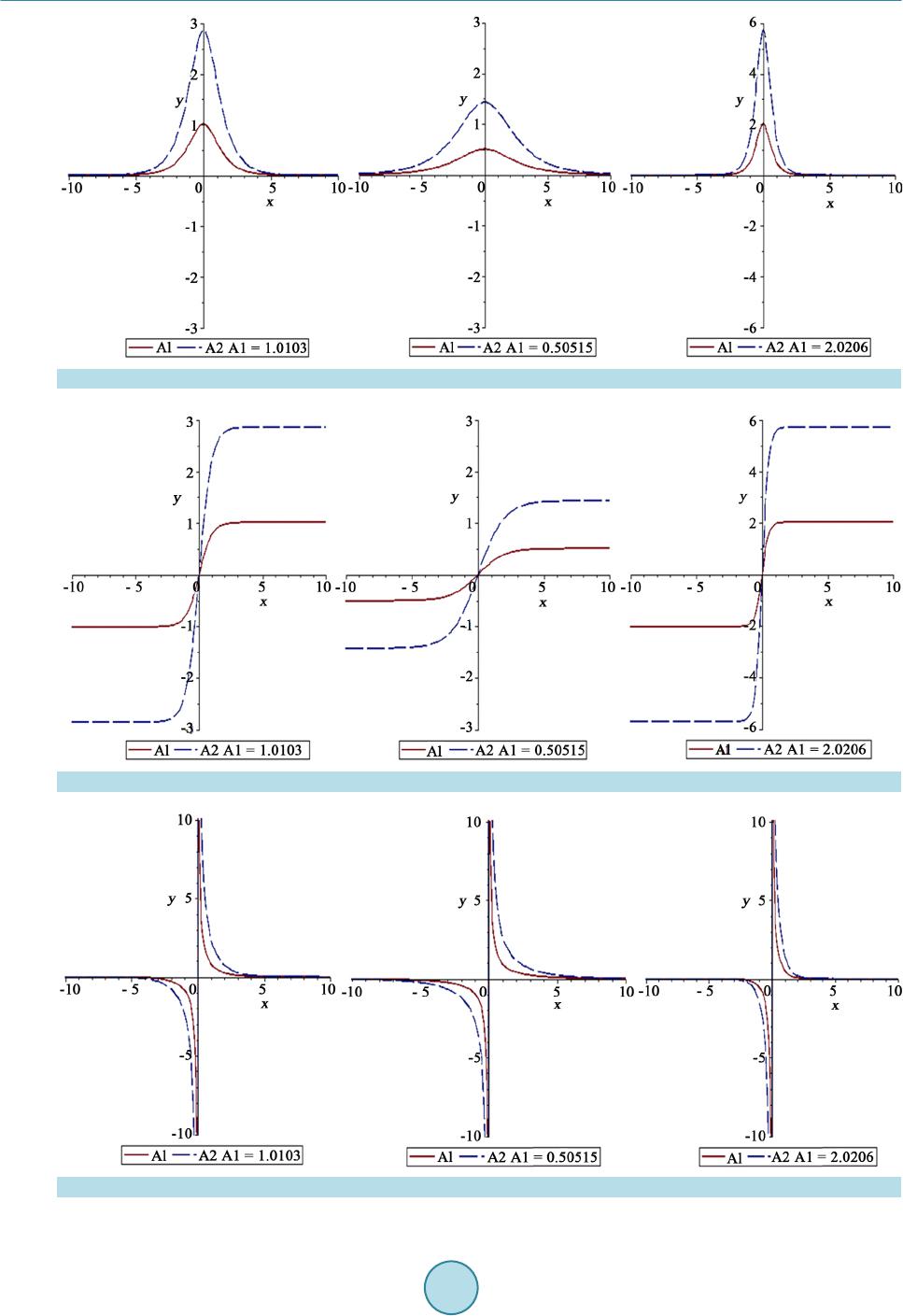

A. A. Al Qarni et al.
1966
Figure 7 . Bright solitons.
Figure 8 . Dark solitons.
Figure 9 . Singular solitons.

A. A. Al Qarni et al.
1967
offset the Schrodinger non-linear. As that finding, those solutions to some numerical methods provide a lot of
add-ons in this study, and this is what we hope implemented with God’s help in the future through the Master
thesis.
References
[1] Biswas, A. (2003) Theory of Optical Couplers. Optical and Quantum Electronics, 35, 221-235.
http://dx.doi.org/10.1023/A:1022852801087
[2] Zakharov, V.E. and Shabat, A.B. (1972) Exact Theory of T wo-Di mensio nal Sel f-Focusing and One-Dimensio nal Sel f-
Modulation of Waves in Non-Linear Media. Journal of Experimental and Theoretical Physics, 34, 62.
[3] Ablowitz, M.J. and Segur, H. (1981) Solitons and H. Segur , Solitons and the Inverse Scattering Tran sfo r m. SIAM, Phi-
ladelphia.
[4] Mihalache, D. and Panoiu, N.C. (1992) Exact Solutions of Nonlinear Schrodinger Equation for Positive Group Veloci-
ty Dispersion. Journal of Mathem ati c al P hy s ic s, 33, 2323. http://dx.doi.org/10.1063/1.529603
[5] Mihalache, D. and Panoiu, N.C. (1993) Analytic Method for Solving the Nonlinear Schrodinger Equation Describing
Pulse Pr opa g a t ion in Dispersive Optic Fibers. Journal of Physics, A26, 2679.
http://dx.doi.org/10.1088/0305-4470/26/11/016
[6] R amos, P.M. and Pavia, C.R. (2000) Self-Routing Switching of Soliton-Like Pulses in Multiple-Core Nonlinear Fiber
Arrays. Journal of the Optical Society of America B, 17, 115.
[7] Biswas, A. (2001) Solitons in Nonlinear Fiber Arrays. Journal of Electromagnetic Waves and Applications, 15, 1189.
http://dx.doi.org/10.1163/156939301X01101
[8] Biswas, A. , Khen, K.R., Rahman, A., Yildirim, A. , Hayat , T. and Aldossary, O.M. (2012) Journal of Optoelectronics
and Advanced Materials, 14, 571.
[9] Sarescu, M., Bhrawy, A.H ., Alsaery, A.A., Hilal, E.M., Khan, K.R., Mahmood, M.F. and Biswas, A. (2014) Optical
Solitons in Nonlinear Directiona l Coupler s with Spation-Temporal Dispersion. Journal of Modern Optics, 61, 441-45 8.
http://dx.doi.org/10.1080/09500340.2014.894149
[10] Banaja, M.A., Alkhateeb, S.A., Alshaery, A.A., Hilal, E.M., Bhrawy, A.H., Moraru, L. and Biswas, A. (2014) Optical
Solitons in Dual-Core Couplers. Wulfenia Journal, 21, 366-380.
[11] Biswas, A., Lott, D.A., Sutton, B., Khan, K.R. and Mahmood, M.F. (2013) Optical Gaussons in Nonlinear Direction al
Couplers. Journal of Electromagnetic Waves and Applications, 27, 1976-1985.