World Journal of Engineering and Technology
Vol.03 No.03(2015), Article ID:60552,7 pages
10.4236/wjet.2015.33C046
A Case Study to Estimate Thermal Conductivity of ABS in Cold Climate Chamber
Umair N. Mughal*, Marina Makarova, Muhammad Shakeel Virk, Geanette Polanco
Atmospheric Icing Research Team, Industrial Engineering Department, Narvik University College, Narvik-8505, Norway
Email: *unm@hin.no


Received 10 September 2015; accepted 15 October 2015; published 22 October 2015

ABSTRACT
Non steady state thermal conductivity of ABS was estimated using an analytical approach in a Cold Climate Chamber at −10˚C and −14˚C. Two hollow cylinders of ABS of varying thickness were used to estimate the conductivity. The material was porous but the porosity was unknown. This paper is a case study to understand, if it is reasonable to estimate the thermal conductivity using the analytical varying thickness approach.
Keywords:
Thermal Conductivity, ABS, Thermocouple, Cold Room, Analytical

1. Introduction
Energy exists in various forms. Thermal energy which is related with heat that can be transferred from one system to another as a result of temperature difference. Energy transfer mechanics can be principally of three types conduction (inside solid), convection (through a fluid) and radiation (electromagnetic emission). From the principle of conduction, thermal conductivity “k” is defined as the property of material to conduct heat flux due to a temperature variation between its ends. Mathematically,
 (1)
(1)
where 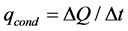 is the amount of heat transferred per unit time and is given in Watts, A is the cross sectional surface area,
is the amount of heat transferred per unit time and is given in Watts, A is the cross sectional surface area, 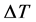 is the temperature difference between the ends and
is the temperature difference between the ends and 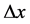 is the distance between the ends.
is the distance between the ends.
There have been different methods and devices developed during the last few decades to experimentally determine the fundamental thermal conductivity of a material. The measurement of thermal conductivity in principle involves the measurement of heat flux and temperature difference across the boundary, nevertheless to determine heat flux is not trivial. Heat flux can however be estimated by an excitation e.g. electric power going into the heater (this is called an absolute measurement), whereas the flux measurement is done by comparison (this is called comparative) [1]. It is very important to carefully consider the configuration of a measurement system and the specimen because they can be effected by the magnitude of thermal conductivity e.g. due to interface heat transfer. The method to determine the thermal conductivity of a material or sample is categorized as:
1. Steady State Technique
2. Non Steady State Techniques or Transient Techniques.
1.1. Steady State Techniques
As name defines, in this technique the temperature change is allowed to stabilize such that 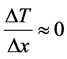 . In this case the experiment have to very well defined and under controlled environment.
. In this case the experiment have to very well defined and under controlled environment.
1.2. Non Steady State Techniques
In this non steady state technique or transient technique the conductivity is measured as the process builds up its heating cycle. This measurement is common in practice as it measures the instantaneous conductivity and then if the techniques allows then they may be averaged. There are many non-steady state conductivity measurement technique, e.g.
a) Transient Plane Source Technique [2] [3]
b) Modified Transient Plan Source Technique [2]
c) Transient Line Source Technique [4]
d) Laser Flash Technique [5]
e) 3w Technique [6] [7]
f) Time Domain Thermoreflectance Method
2. Model
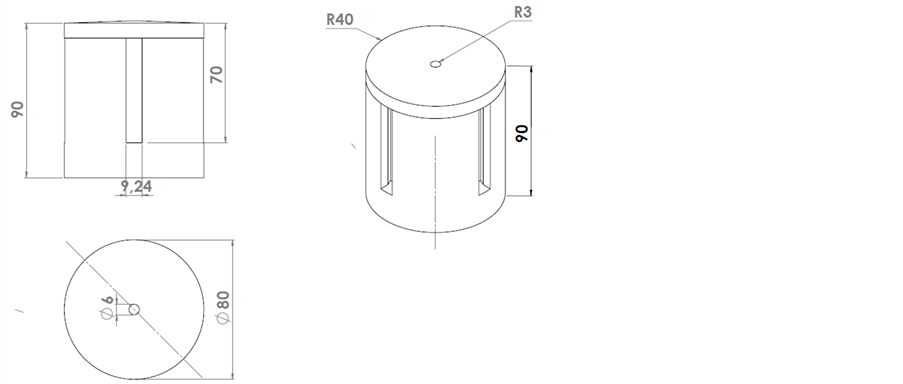
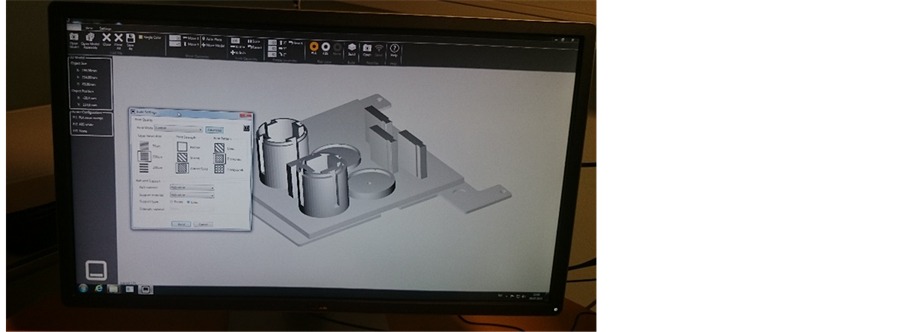
Atmospheric icing research team at Narvik University College is developing an atmospheric icing sensor which is potentially capable to detect icing event, icing type, icing load, icing rate, melting rate. The final material of this icing sensor is aluminium, nevertheless to evaluate the option of using ABS (Acrylonitrile butadiene styrene) as one of the potential material, the thermal conductivity of ABS was important to estimate in freezing domain. The geometry of this model was a scaled down model of the rotating part of the actual sensor which was produced through rapid prototyping machine CubePro Duo (Figure 1). The CAD Model was developed using Solid Works and the dimensions are given in Figure 2.
Figure 1. CubePro Duo.
Figure 2. Dimensions of model.
The layer resolution for this model was “200 mm” and the print strength was “almost solid” whereas the print pattern was “diamonds”. These settings can be seen in Figure 3 and the manufactured model can be seen in Figure 4. The porosity and the exact chemical composition of this model were however not well determined.
3. Experimental Procedure
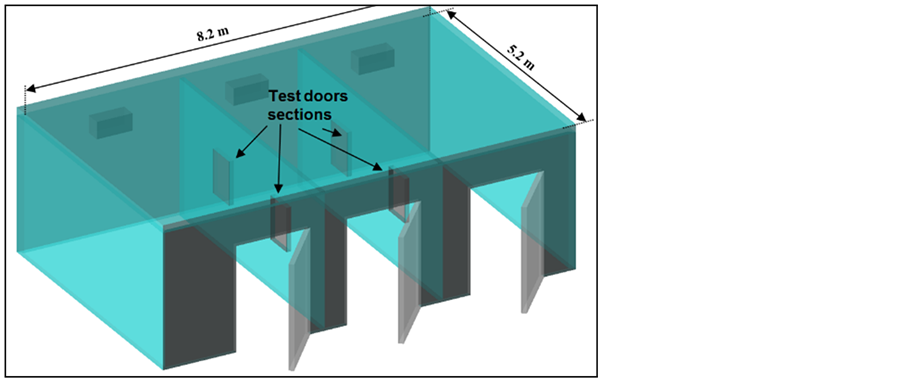
Narvik University College have three Cold Room Facilities for experimentation (see Figure 5). The controlled temperature limits are −30˚C to 20˚C. At a desired intermediate setting, the temperatures however do not remain fixed for a very long time because the temperature is being maintained by a compressor which stops immediately as soon as the temperature reaches the desired setting. It then automatically restarts as the temperature of the Cold Room is increased by DT > 1˚C or more than the desired setting. Nevertheless the cold chamber have enough insulation to maintain the temperature for a short duration. Also a minor source of error is the small window which is used to link electronic systems in the Cold Chamber and the outside world.
The main idea of this work was to estimate non steady state or transient thermal conductivity of the material by analyzing heat transfer through two hollow cylinders of different thicknesses: 5 and 10 mm. The thermocouples were mounted on the geometries, as can be seen in Figure 6 and Figure 7. To meet the data acquisition NI cDAQ 9172 Chassis is used. Two 4 channel thermocouple input modules (NI 9211) were used and analysis was done using Labview Professional Development System (License Number J10X42041). The J-type thermocouples were connected with 9211 Module (see Figure 8) and data was analyzed.
The experiment table was arranged as shown in Figure 6. Two experiments were then performed at two different controlled temperatures of Cold Chamber. The adjusted temperatures were -10ºC and -14ºC. After setting the first temperature e.g. −10˚C the system was left for 24 hours each. The data was saved into .txt file.
4. Analytical Analysis
As shown in Figure 6 and Figure 7, the attached thermocouples are numbered 1-7. Below mentioned heat transfer principles are understood to take place through these points:
1 - 2 Convection A (is the heat transfer from surrounding area to the outer surface of the model 1);
2 - 3 Conduction B (is the heat transfer from outer surface to inner surface of the model 1, in other words it is conduction through the wall);
3 - 4 Convection C (is the heat transfer from inner wall to the inner area of model 1)
1 - 5 Convection D (is the heat transfer from surrounding area to the outer surface of the model 2);
5 - 6 Conduction E (is the heat transfer from outer surface to inner surface of the model 2, in other words it is conduction through the wall)
6 - 7 Convection F (is the heat transfer from inner wall to the inner area of model 2)
Figure 3. Rapid prototyping print setting.
Figure 4. Manufactured model.
Figure 5. Cold climate chambers at NUC.
Figure 6. Cylinders in cold climate chamber.
Figure 7. Schematic of thermocouples attachments.
Figure 8. Thermocouples attachment in DAQ system.
Hence total heat transfer for the model 1 then is equal to:
q1 = Convection A + Conduction B + Convection C (2)
q2 = Convection D + Conduction E + Convection F (3)
where q1 is the heat transfer rate for model 1 and q2 is the heat transfer rate for model 2. Both of the models are located in the same surrounding conditions, hence it is reasonable to assume that the heat transfer rate can be equated q1 = q2. Therefore,
Convection A + Conduction B + Convection C = Convection D + Conduction E + Convection F (4)
Therefore from Equation 4 and Table 1, we find
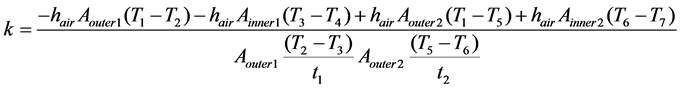 (5)
(5)
The inner and outer areas and all other dimensions of the two cylinders were found using the CAD package where these geometries were created (see Table 2). These values were then used to calculate thermal conductivity using Equation 5 and Table 2.
5. Results
From each experiment, the instantaneous conductivity was measured for a period of 24 hours. The samples were then averaged. The results for each experiment are shown in Figure 9 and the results are tabulated in Table 3.
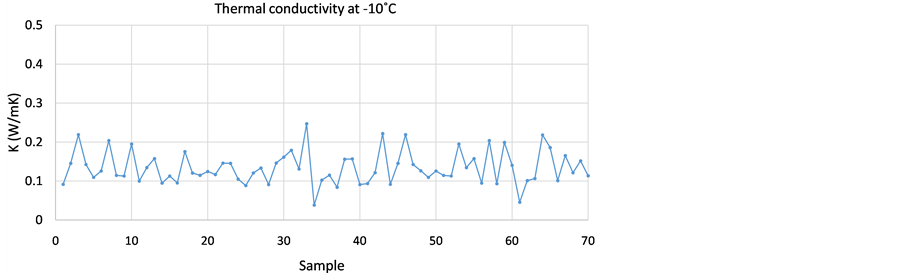
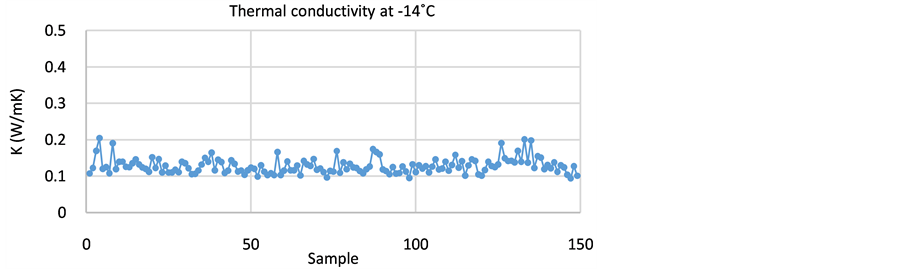
Figure 9. Two experiments to determine non-steady state thermal conductivity of ABS. (a) T = −10˚C; (b) T = −14˚C.
Table 1. Model 1 and model 2 conduction and convection relationships.
Table 2. Model 1 and 2 dimensions.
Table 3. Estimated and standard thermal conductivity of ABS.
6. Conclusions and Discussions
In this work, the thermal conductivity of ABS was estimated using an analytical approach by measuring the temperature distribution across the cylindrical geometries. The deviation between the analytically estimated and standardized limit values of ABS may be because of the following reasons,
1) This ABS used in this experiment was have porosity larger than 0 and it has the print pattern of diamonds therefore it has some air pockets (kair = 0.021 W/mC).
2) There may be some chances of inadequate insulation of the both hollow cylinders which may have affected the results.
3) There may be chances of inadequate thermocouple attachments on the cylinders as the epoxy have less stickiness in freezing domains.
4) Also the exact limit values of ABS from 0.188 till 0.335 W/mC are based upon the composition of ABS as can be seen in Honeycutt [8]. However in the manufactured samples the chemical composition was also not well determined.
The results of Experiment 2 at −14˚C have less non steady state thermal conductivity fluctuations than the results of Experiment 1 at −10˚C because of the reason that in second experiment there were low variations in cold chamber temperature as mentioned in Section 3. Nevertheless it is found that this approach to estimate thermal conductivity of a material by varying thickness of two geometries and testing it in cold chamber facility is sufficiently adequate and can be utilized for future experimentations at least to estimate the thermal conductivity of any material with unknown properties and composition. The results of this analysis can also be improved by introducing interface heat transfer principle in this thickness variation principle.
Acknowledgements
The work reported in this research paper was carried out by Atmospheric Icing Research Team at Industrial Engineering Department of Narvik University College and was funded by Research Council of Norway, project no. 195153 (ColdTech RT3 and RT5) and Norwegian Centre for International Cooperation in Education, project number- HNP-2014/10023.
Cite this paper
Umair N. Mughal,Marina Makarova,Muhammad Shakeel Virk,Geanette Polanco, (2015) A Case Study to Estimate Thermal Conductivity of ABS in Cold Climate Chamber. World Journal of Engineering and Technology,03,309-315. doi: 10.4236/wjet.2015.33C046
References
- 1. Principal Methods of Thermal Conductivity Measurements. http://thermophysical.tainstruments.com/PDF/technotes/TPN-67%20Principal%20Methods%20of%20Thermal%20Conductivity%20Measurement.pdf
- 2. Suleiman, B.M. and Malinaric, S. (2006) Transient Techniques for Meas-urements of Thermal Properties of Solids: Data Evaluation within Optimized Time Intervals. WSEAS Transactions on Heat and Mass Transfer, 1, 8.
- 3. Gustafsson, S.E. (1991) Transient Plane Source Techniques for Thermal Conductivity and Thermal Diffusivity Measurements of Solid Materials. Review of Scientific Instruments, 62, 797. http://dx.doi.org/10.1063/1.1142087
- 4. Healy, J.J., de Groot, J.J. and Kestin, J. (1976) The Theory of the Transient Hot-Wire Method for Measuring Thermal Conductivity. Physica B+C, 82, 17. http://dx.doi.org/10.1016/0378-4363(76)90203-5
- 5. Parker, W.J., et al. (1961) Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity. Journal of Applied Physics, 32, 1697. http://dx.doi.org/10.1063/1.1728417
- 6. Wang, H. and Sen, M. (2009) Analysis of 3-Omega Method for Thermal Conductivity Measurement. International Journal of Heat and Mass Transfer, 52, 2102-2109. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2008.10.020
- 7. Lu, L., Yi, W. and Zhang, D.L. (2002) A 3-Omega Method for Specific Heat and Thermal Conductivity Measurements. Review of Scientific Instruments, 72.
- 8. Thermal Conductivity of ABS. http://www.grantadesign.com/education/datasheets/ABS.htm
NOTES
*Corresponding author.