World Journal of Engineering and Technology
Vol.03 No.03(2015), Article ID:60549,7 pages
10.4236/wjet.2015.33C045
An Improved Iterative Closest Points Algorithm
Hao Yang1*, Jialan Jiang2, Guowei Zhao1, Jie Zhao1
1School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing, China
2School of Mechanical Engineering, University of Science and Technology, Beijing, China
Email: *15210965998@163.com


Received 12 September 2015; accepted 15 October 2015; published 22 October 2015

ABSTRACT
Visual method including binocular stereo vision method and monocular vision method of the relative position and pose measurement for space target has become relatively mature, and many researchers focus on the method based on three-dimension measurement recently. ICP alignment, which is the key of three-dimension pattern measurement method, has the problem of low efficiency in large data sets. Considering this problem, an improved ICP algorithm is proposed in this paper. The improved ICP algorithm is the combination of the original ICP algorithm and KD-TREE. The experimental comparison between the improved ICP algorithm and the traditional ICP algorithm in efficiency has been given in this paper, which shows that the improved ICP algorithm can get much better performance.
Keywords:
The Relative Position and Pose Measurement of Space Target, ICP Algorithm, KD-TREE

1. Introduction
The space target has been carried out in orbit demonstration of real experiment currently, a method based on two dimensional vision image technique is one of the most common approach in relative position and pose measurement of space target, such as the closing camera system on ETS-VII [1], the frequency measurement system on ATV et al. [2]. But the two dimensional visual sensor can only provide sight angel information, it can not provide distance information, which is a problem of poor observe ability in the measurement.
Based on the three-dimensional shape measurement, a particular light is projected on the target, it is modulated by the target. Through demodulated, the three dimensional information of target can be get. Since the structure of the target remains unchanged in a very short time, it can be regarded as a rigid body, so different times of the three-dimensional data include a posture change of the target, there is a certain space similarity transformation relationship between the data, so the data of the t + 1 moment can be regarded as a rotation about a spatial coordinate system of the t moment. Thus, through registering the different three-dimension data of the target, the relative posture change of target to the measuring device can be obtained.
ICP algorithm is a kind of matching algorithms which is mostly used in three-dimension point cloud registration. It is based on the iterative optimization matrix. In each iteration, each point of the target point set is focused to find the nearest point of the reference point set. Using these closest points, the corresponding rotation matrix and translation vector is calculated. Through the calculated rotation matrix and translation vector, a new point set changed by the target point set can be got, then the algorithm goes into the next iteration. Finally, the best optimal transformation matrix and the accurate registration between two set of points is achieved [3]. The efficiency of the originally proposed ICP algorithm is not very high, the main problem is to find the corresponding point, it requires each point of the target point set and the reference point set is compared to determine the neatest distance. Considering the above problem, many researchers have made a lot of improvements, such as:
(1) The use of tangent plane to approach point cloud [4], the final resolution is to find the least square distance of the tangent, but the efficiency is still very low.
(2) The use of ICL algorithm, by directly focus on the line of the two point sets and use the corresponding line registration instead of point registration [5].
An improved ICP algorithm based on KD-TREE is proposed in this paper. It is based on the traditional ICP algorithm, but it uses KD-TREE to search the nearest points [6]. The corresponding point set is stored in the KD-TREE. KD-TREE can arrange the point set more effectively, and then establish the relationship between the discrete points. Through the relationship, KD-TREE can speed up the search of corresponding points. The efficiency of the algorithm is greatly improved through this method.
2. Traditional ICP Algorithm
ICP (Iterative Closest points) algorithm is a three-dimensional matching algorithm. The key of the algorithm is called the corresponding point set registration algorithm. The corresponding point set registration algorithm is to solve the coordinate transformation matrix and find the relationship between the point sets. Through the relationship, the registration is completed.
The quaternion method is used to solve the transformation matrix between the two point sets [7]. If the two point sets exist in some coincidence parts, setting the coincidence part of target point set as P and setting the coincidence part of reference point set as Q, the corresponding point set should meet the following conditions:
(1) The number of P is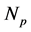 , the number of Q is
, the number of Q is , and
, and 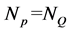
(2) For each point 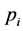 of P should be corresponded to
of P should be corresponded to 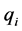 of Q
of Q
The rotation vector is supposed an unit quaternion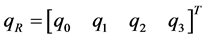 ,
, 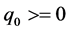 , and
, and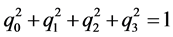 , a
, a  rotation matrix
rotation matrix 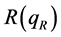 can be got. Then take the translation vector
can be got. Then take the translation vector , and the
, and the
complete coordinate transformation matrix is . In order to best match the two point sets, the distance between the corresponding points set should be the minimum. The final solution of the coordinate transformation is to solve q to find the minimum value of the following objective function.
. In order to best match the two point sets, the distance between the corresponding points set should be the minimum. The final solution of the coordinate transformation is to solve q to find the minimum value of the following objective function.
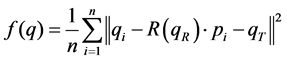 (1)
(1)
The process of the traditional algorithm is as follows:
Step 1: Get the target point set P and the reference point set Q;
Step 2: Calculate the center of P and Q;
 (2)
(2)
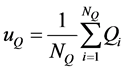 (3)
(3)
Step 3: Construct the Covariance matrix of P and Q;
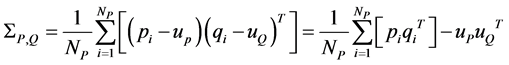 (4)
(4)
Step 4: Construct a  symmetric matrix of the Covariance matrix;
symmetric matrix of the Covariance matrix;

In this matrix, 


Step 5: Calculate the eigenvalues and eigenvectors of

Step 6: Calculate the best translation vector;

In Equation (7):

Step 7: Get the final coordinate transformation vector 

Step 8: End
As a three-dimensional point cloud registration algorithm, ICP algorithm can be summarized as some following steps: First, find the closest point between the reference point set and the target point set in each iteration, and calculate the coordinate transformation vector and error by using these closest points, and then get the new point set in next iteration until the error meeting the given conditions by employing the coordinate transformation vector and error on the target point set next. Finally, the final transformation vector can be got. Although the ICP algorithm is widely used in various fields, the efficiency is very low especially for large scale data sets. It wastes a lot time to find the closest points. Considering this problem, a new method mentioned in the later part is proposed to improve the traditional ICP algorithm.
3. ICP Algorithm Based on KD-TREE
The efficiency of the traditional ICP algorithm is the most important problem, so this paper gives an improved ICP algorithm based on KD-TREE to solve this problem, through the effective management of the point sets, the relationship between the discrete points can be established, and the registration efficiency can be improved greatly.
3.1. Construct KD-TREE
Select a sample 





method of dividing the sample set is shown in Equation (9). Set a left sub-tree when the dimension is less than the coordinate point and set a right sub-tree when the dimension is bigger than the coordinate point. Then continue to construct tree of the left sub-tree and right sub-tree, select the second dimension (



In Equation (9), k is the dimension and one-dimension represents a property of the multidimensional space. Exsetleft is the left sub-tree and exsetright is the right sub-tree. A sketch map of KD-TREE established in MATLAB is shown as Figure 1
For the division of KD-TREE, different ways will produce different KD-TREE, one is divided according to the density of the points, and another is divided according to the middle of dividing line.
3.2. Find the Nearest Point through KD-TREE
Using the constructed KD-TREE to find the minimum norm distance of the target point is the nearest point search of KD-TREE. Using KD-TREE to find the nearest point, a hyper rectangle hr and a hyper circle should be defined, the center of the hyper circle is t and the radius is r, by comparing the distance between the hyper rectangle and hyper circle, the nearest point p in the hyper rectangle to the center of the hyper circle (t) is found. The comparison method is shown in Equation (10).

As shown in Equation (10), if the two norm distance to t is smaller than r, the hyper rectangle and the hyper circle is intersected. Firstly, the algorithm compares the distance of the point to toot node. Secondly, it determine s whether the left sub-tree or right sub-tree should be used based on the dimension of the point and the root node.
Due to the effective management of point cloud data based on KD-TREE, the average searching length is

The process of the improved algorithm based on KD-TREE is shown in Figure 2. It contains some following steps:
Step 1: Get the target point set and the reference point set. The number of the target point set is NP and the number of the reference point set is NQ;
Step 2: Initialize

Step 3: Use KD-TREE to find the nearest point of P in Q,
Step 4: Use the corresponding point set registration algorithm to calculate the coordinate transformation vector 
Step 5: Apply the coordinate transformation
Figure 1. A sketch map of KD-TREE established in MATLAB.
Figure 2. The process of the algorithm based on KD-TREE.
Step 6: Determine whether the error converges, if
Step 7: Get the final coordinate transformation
Step 8: End
The time efficiency of the ICP algorithm is mainly reflected on the search of nearest points, in the traditional algorithm, it needs to compare every point and find the nearest point. If the size of the point set is very large, it will take a lot time. Improved algorithm based on the KD-TREE makes up the shortcoming of the traditional algorithm. Above all, the improved ICP algorithm is better than the traditional algorithm, it does not need to compare all the points in the search of the nearest points.
4. Simulation Experiment
In this part, two experiments are done to compare the efficiency of the two algorithms. The first experiment is to compare the time efficiency when the number of the target point set and reference point set is same. The second experiment is to compare the time efficiency when the number of the target point set and reference point set is different.
4.1. First Experiment
Randomly generate reference point set Q which has N points, in order to understand the registration effect of ICP algorithm, the target point set which has N points is produced by rotation and translation of the reference point set. Both of the algorithms are finished on MATLAB. Experiments are done on several different data sets. The experimental results are shown in Table 1 and Figure 3
From Table 1 and Figure 3, when the size of the reference point set and the target point set is same, the registration time of the traditional algorithm changes longer and longer with the size of the point set increasing. And the registration time of the improved algorithm changes a little with the size of point set increasing. When the size of the two algorithms is same, the time of improved algorithm is much less than the traditional algorithm and with the size increasing, the difference is more obvious.
4.2. Second Experiment
Randomly generate reference point set Q which has N points, taking the first 5000 points of Q as the target point set and then rotate it and translate it. The experimental environment is the same as the first experiment. The experimental results are shown in Table 2.
From Table 2, it can be concluded that when the size of the reference point set is different and the size of the target point set remains the same, the efficiency of the improved algorithm based on KD-TREE is much better
Figure 3. The registration time of two algorithms.
Table 1. Two kinds of ICP algorithms registration speed at the same ponit size.
Table 2. Two kinds of ICP algorithms registration speed at the different ponit size.
than traditional algorithm.
Through these two experiments, it can be concluded that the improved ICP algorithm based on KD-TREE is much better than traditional ICP algorithm.
Take the size of reference point set and target data point as
5. Conclusion
ICP algorithm is widely used in three-dimensional point cloud registration, for the large data sets, its efficiency is very low, this paper presents an improved ICP algorithm based on KD-TREE, In this method, the data is stored and managed by KD-TREE, it uses KD-TREE to search the nearest point and fully takes advantage of KD-TREE in the data index search, it solves the problem of low efficiency of traditional ICP algorithm. Through the experimental results, it can be concluded that the improved ICP algorithm based on KD-TREE is much better than the traditional algorithm, in practical applications, the size of the data sets is relatively large. Therefore, the improved ICP algorithm based on KD-TREE is expected to register the point clouds.
Figure 4. The original data set.
Figure 5. The data set changed by the ICP algorithm based on KD-TREE.
Acknowledgements
This paper is completed under the guidance of my tutor Guowei Zhao, so I want to express my best wishes to him.
Cite this paper
Hao Yang,Jialan Jiang,Guowei Zhao,Jie Zhao, (2015) An Improved Iterative Closest Points Algorithm. World Journal of Engineering and Technology,03,302-308. doi: 10.4236/wjet.2015.33C045
References
- 1. Kawano, I., Mokuno, M., Kasai, T. and Suzuki, T. (2001) Result of Autonomous Rendezvous Docking Experiment of Engineering Test Satellite-VII. Journal of Spacecraft and Rockets, 38, 105-111. http://dx.doi.org/10.2514/2.3661
- 2. Mokuno, M. and Kawano, I. (1994) Engineering Test Satellite VII Rendezous Docking Optical Sensor System. AIAA 3698, 1314-1322.
- 3. Zhang, G.P., Zhang, Y.L. and Guo, Z. (2006) 3D Face Registration Based on ICP and Accurate Analysis of the Spindle. Computer Engineering and Application, 42, 62-64. http://dx.doi.org/10.3321/j.issn:1002-8331.2006.29.019
- 4. Chen, Y. and Medioni, G. (1991) Object modeling by Registration of Multiple Range Images. Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, 9-11 April 1991, 2724-2729. http://dx.doi.org/10.1109/ROBOT.1991.132043
- 5. Li, Q. and Griffiths, J.G. (2000) Iterative Closest Geometric Objects Registration. Computer and Mathematic with Application, 40, 1171-1188. http://dx.doi.org/10.1016/S0898-1221(00)00230-3
- 6. Bentley, J.L. (1975) Multi Dimensional Binary Search Trees Used Associative Searching. Communication of the ACM, 18, 509-517.
- 7. Dai, J.L., Chen, Z.Y. and Ye, X.Z. (2007) Application of ICP Algorithm in Point Cloud Registration ICP. Journal of Image and Graphics, 12, 517-521.
NOTES
*Corresponding author.














