Received 13 August 2015; accepted 15 October 2015; published 22 October 2015

ABSTRACT

We investigate Gaver’s parallel system attended by a cold standby unit and a repairman with multiple vacations. By analysing the spectral distribution of the system operator and taking into account the irreducibility of the semigroup generated by the system operator we prove that the dynamic solution converges strongly to the steady state solution. Thus we obtain asymptotic stability of the dynamic solution of the system.

Keywords:

Gaver’s Parallel Pystem, C₀-Semigroup, Irreducibility, Asymptotic Stability

1. Introduction

Repairable system is not only a kind of important system discussed in reliability theory but also one of the main objects studied in reliability mathematics. ”Repairable” means that if a failure in the system occurs it can be repaired and then the system works normally again. The Gaver’s Parallel system, as one of the classical repairable systems in reliability theory, has been given much attention in previous literatures, see [1]-[3]. In [4], the authors studied Gaver’s parallel system attended by a cold standby unit and a repairman with multiple vacations and obtained some reliability expressions such as the Laplace transform of the reliability, the mean time to the first failure, the availability and the failure frequency of the system by using the supplementary variable method and the generalized Markov progress method as well as the Laplace-transform technique. In [4], the authors used the dynamic solution and its asymptotic stability in calculating the availability and the reliability. But they did not discuss the existence of the dynamic solution and the asymptotic stability of the dynamic solution. In [5], we proved the well-posedness and the existence of a unique positive dynamic solution of the system by using 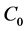- semigroup theory of linear operators from [6] and [7]. In this paper, we prove that the dynamic solution converging to its static solution in the sense of the norm using the stochastic matrix and irreducibility of the corresponding semigroup, thus we obtain the asymptotic stability of the dynamic solution of this system.

The system can be described by the following partial differential equations (see [4]).

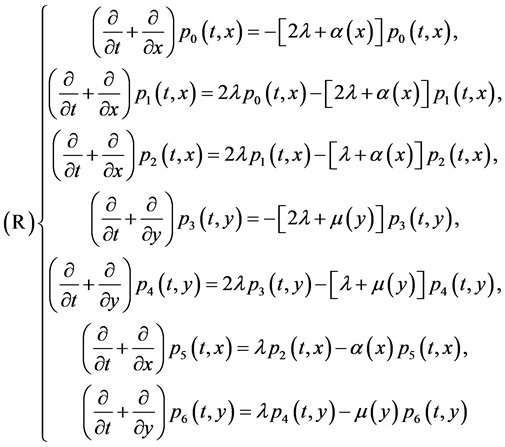
with the boundary condition

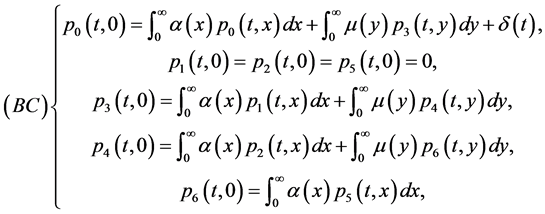
and the initial condition

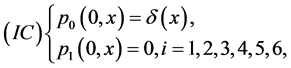where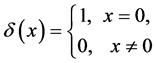

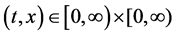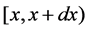Here; gives the probability that at time t two units are operating, one unit is under standby, the repairman is in vacation, the system is good and the elapsed repair time lies in; represents the probability that at time 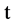two units are operating, one unit is waiting for repair, the repairman is in vacation, the system is good and the elapsed repair time lies in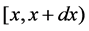; 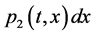represents the probability that at time 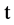two unit is operating, one unit is waiting for repair, the repairman is in vacation, the system is good and the elapsed repair time lies in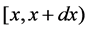; 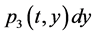represents the probability that at time 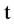two units are operating, one unit being repaired, the system is good and the hours that the failed unit has been repaired lies in; represents the probability that at time one unit is operating, one unit being repaired, one unit is waiting for repair, the system is good and the hours that the failed unit has been repaired lies in; represents the probability that at time three units are waiting for repair, the repairman is in vacation, the system is down and the elapsed repair time lies in; represents the probability that at time one unit being repaired, two unit is waiting for repair, the system is down and the hours that the failed unit has been repaired lies in; are positive constants; is the vacation rate function; is the repair rate function.

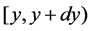Throughout the paper we require the following assumption for the vacation rate function and the repair rate function.

General Assumption 1.1: The functions and are measurable and bounded such that

2. The Abstract Cauchy Problem

To apply semigroup theory we use the same method in [5] to rewrite in this section the system, , as an abstract Cauchy problem ([6], Def.II.6.1) on the Banach space, where

and

.

To define the system operator we introduce a “maximal operator” on X given as

, where

To model the boundary conditions (BC) we take the “boundary space” and then define “boundary operators” and as follows.

and

,

where,

If the system operator on is then defined as

,

Then the above equations and are equivalent to the abstract Cauchy problem

(ACP)

By a direct computation we obtain the explicit form of the elements in as follows.

Lemma 2.1: For, we have

(1)

We define the operator as

And then using ([8], Lemma 1.2), the domain of the maximal operator decomposes as

.

Moreover, since is surjective,

is invertible for each, see ([8], Lemma 1.2]. We denote its inverse by

and call it “Dirichlet operator”.

We can give the form of as follows, see [5].

Lemma 2.2: For each, the operator has the form

,

where

For, the operator can be represented by the -matrix

,

where

To prove the asymptotic stability of the dynamic solution of the system we apply the following result, which can be found in [9].

Lemma 2.3 (The characteristic equation): Let, then

(i).

(ii) If and there exists such that, then

.

We obtained the following results in [5].

Theorem 3.4: The operator generates a positive contraction -semigroup.

Theorem 3.5: The associated abstract Cauchy problem is well-posed.

Theorem 3.6: The system and has a unique positive dynamic solution

.

3. The Asymptotic Stability of the Dynamic Solution

In this section, we will investigate the asymptotic stability of the dynamic solution of the system. We show first the following lemmas:

Lemma 3.1: For the operator we have.

Proof: By a straightforward calculation we see that the matrix is column stochastic and thus. Applying Lemma 2.3 (i), we immediately obtain.

Using Lemma 2.3 (ii) we can show that 0 is the only spectral value of A on the imaginary axis.

Lemma 3.2: The spectrum of A satisfies.

Proof: If,then it is not difficult to derive that, thus the spectral radius fulfills. This implies. By Lemma 2.3 (ii) we obtain that for all，, i.e.,

We can express the resolvent of in terms of the resolvent of, the Dirichlet operator and the boundary operator in the following way.

Lemma 3.3: If,then.

Lemma 3.4: The semigroup generated by is irreducible.

Proof: We can see as in ([9], Lemma 3.9) that transforms any positive vector into a strictly positive vector. Using ([7], Def. C-III 3.1) this implies that the semigroup generated by is irreducible.

With this at hand one can then show the convergence of the semigroup to a one dimensional equilibrium point, see ([9], Th. 3.11).

Theorem 3.5: The space can be decomposed into the direct sum

where is one-dimensional and spanned by a strictly positive eigenvector of. In addition, the restriction is strongly stable.

Corollary 3.6: For all, there exists, such that

where

Applying the above corollary, we now obtain our main result as follows.

Corollary 3.7: The dynamic solution of the system and converges strongly to the steady-state solution as time tends to infinity, that is,

where and as in Corollary 3.6.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 11361057).

Cite this paper

Abdukerim Haji, (2015) Asymptotic Stability of Gaver’s Parallel System Attended by a Cold Standby Unit and a Repairman with Multiple Vacations. World Journal of Engineering and Technology,03,277-283. doi: 10.4236/wjet.2015.33C041

References