World Journal of Engineering and Technology
Vol.03 No.03(2015), Article ID:60496,8 pages
10.4236/wjet.2015.33C017
Study on Torque Ripple of Wound-Field Doubly Salient Generator with No Load
Fan Yang, Jin Ma, Haoji Xu
Department of Electrical Engineering, AVIC LEIHUA Electronic Technology Research Institute, Wuxi, China
Email: mafeng1705@126.com


Received 8 September 2015; accepted 15 October 2015; published 22 October 2015

ABSTRACT
Wound-field Doubly Salient Generator (WFDSG) has the outstanding advantages of simple structure, high reliability and controllable excitation. However, there exists obvious torque ripple in generator’s input torque, which has restricted its applications. Based on the concept of electromagnetic torque of WFDSG, the nonlinear formula under no load condition has been derived. Furthermore, it is proved to be reasonable theoretically in comparison with linear and approximate nonlinear formulas. Based on the 12/8 salient prototype, the correctness of nonlinear formula has been verified by comparing the results of virtual displacement method with the results of finite element analysis. At last, the simulation results have been validated by experiments.
Keywords:
WFDSG, Torque Ripple, Nonlinear Formula

1. Introduction
WFDSG is a new type of brushless electrical machine, whose structure and manufacturing process are simple with high reliability, low cost. Thus, WFDSG has an excellent potential in generator of automotive and airplane [1]. However, just as the reluctance motor, WFDSG has the disadvantage of obvious torque ripple, which makes large vibration, noise and poor efficiency. On the other hand, this obvious torque ripple leads to large fatigue stress, reducing the service life of the shaft. Thus, in order to increase the service life of the shaft and generating efficiency, it is essential to study the torque ripple of WFDSG.
At present, the study of torque ripple is mainly focus on Doubly Salient Permanent-magnet Generator, but rarely on WFDSG [2]. The main study method on WFDSG is linear or approximate nonlinear. Because of the stator and rotor having the structure of salient pole, the obvious fringe effect and local saturation can be observed when motor works normally. So it is difficult for analytical algorithm since the electromagnetic torque (Tem for simplification) is the nonlinear function of rotor position, exciting current and winding current. Paper [3] introduces an analytical formula of WFDSG in linear mode. The formula ignored the saturation of magnetic circuit, which means the value of inductance stays constant despite the variation of the current. Paper [4] introduces an approximate nonlinear model which takes the saturation of magnetic circuit into account. However, in case of super saturation of magnetic circuit, the analytical algorithm can’t meet the reality well.
To simplify the analysis, a 12/8 salient prototype in lab will be studied in this paper. The lamination and major dimension of the WFDSG are shown in Figure 1 and Table 1.
2. Comparison of Electromagnetic Torque Formulas
The three-phase armature current is zero with no load. There is exciting current if if it is excited by voltage source. From paper [5], Tem of the three-phase WFDSG can be given as
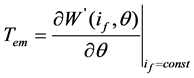 (1)
(1)
where θ refers to rotor position angle, W’ (if, θ) refers to magnetism co-energy, which is the function of if and θ. If the rotor has a certain value of position angle θn, the exciting current has the value of ifn. In this way, Equation (1) can be written as a differential operator
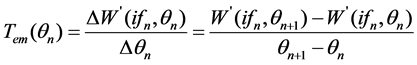 . (2)
. (2)
As long as the difference of exciting current ifn at θn+1 and θn is a constant, the ratio of the different magnetism co-energy ΔW’(ifn, θn) (ΔW’ for simplification) and Δθ is the Tem. This method can be called virtual displacement method. In this way, the area of ΔW’ determines the accuracy of the different methods.
Figure 1. Lamination for 12/8 WFDSG.
Table 1. Major dimension and material details of the motor.
2.1. Nonlinear Formula
Change the Equation (1) into the integration of flux linkage
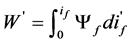 (3)
(3)
where Ψf refers to self-inductance flux linkage in the exciting coils. It’s a function of if and θ. Replacing Equation (1) with Equation (3) and the Tem nonlinear equation can be written as
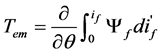 (4)
(4)
It can be found from Equation (3) and Equation (4) that the corresponding ΔW’ at certain position angle θn is
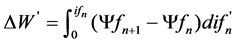 (5)
(5)
The area of ΔW’ is shown as dash area in Figure 2. At the position angle θn, magnetic energy operation position is point a (ifn, Ψfn), at the position angle θn+1, magnetic energy operation position is point b (ifn, Ψfn+1). The area enveloped by oab is ΔW’, whose independent variable is ifn, integrating by Ψfn+1 − Ψfn.
2.2. Approximate Nonlinear Formula
Paper [4] proposes an approximate nonlinear formula of Tem with no load:
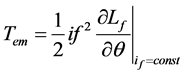 (6)
(6)
Meanwhile, at the rotor position angle θn, the formula of Tem can be written as differential operator:
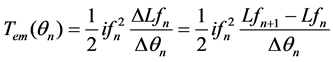 (7)
(7)
Combined with Equation (2) and Equation (7), the ΔW’ can be written as:
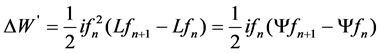 (8)
(8)
The area enveloped by ΔW’ is shown in Figure 3.
The magnetic energy operation positions of approximate nonlinear formula and nonlinear formula are same: at the position θn, corresponds with point a (ifn, Ψfn), namely (ifn, ifnLfn). At the position θn+1, corresponds with point b (ifn, Ψfn+1), namely (ifn, ifnLfn+1). The only difference is approximate nonlinear formula has the area of ΔW’ enveloped by Δoab, not oab. From the graph it can be found that as long as Δoab is small enough, the area of Δoab can be equal to oab approximately. Meanwhile, it can be found that the saturation gets deeper with increasing of if, the difference between Δoab and oab gets larger.
Figure 2. ΔW’ for nonlinear formula.
Figure 3. ΔW’ for approximate nonlinear formula.
2.3. Linear Formula
Paper [3] proposes a linear Tem formula with no load.
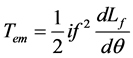 (9)
(9)
Referring to the method introduced in 2.2, the linear formula of ΔW’ is written as:
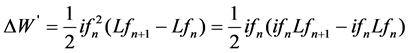 (10)
(10)
The magnetic energy operation position of this method is different from those of methods mentioned before. The position θn corresponds the point a (ifn, Ψfn), namely (ifn, ifnLfn). The position θn+1 corresponds the point b (ifn+1, ifn+1 Lfn+1). Figure 4 shows the ΔW’ sketch map. Figure 4(a) refers to the situation when ifn < ifn+1 while Figure 4(b) refers to ifn > ifn+1.
In Equation (10), ifn Lfn refers to ordinate of the magnetic energy operation position a while ifn Lfn+1 doesn’t refers to the magnetic energy operation position b. The magnetic energy operation position should be the point c, which is the cross point of ob and if = ifn. Thus, the area of Δoac should be ΔW’. It is obvious that the area of Δ oac is different from that of oab. It is same as the situation when ifn > ifn+1.
All the mentioned above is based on nonlinear magnetic circuit. As for linear magnetic circuit, it’s easy to get the same results with the nonlinear, approximate nonlinear and linear formulas. Table 2 shows the formulas and application area of Tem.
3. The Calculation and Simulation of Nonlinear Tem Formula
3.1. Calculation Method
In order to get the analytical solution, it is necessary to get the area of ΔW’ in Figure 1. ifn can be divided into m parts, ifn, ifn2, ifn3…ifnm. Each parts equals to ifn/m. All these points divides the curve into m parts, S1, S2, S3…Sm, as shown in Figure 5.
If every part of S can be calculated, the summation of all these parts is ΔW’. When the current is ifn, the corresponding flux linkage of θn+1 and θn are Ψf(n+1)1 and Ψfn1. If m is large enough, the area of S1 can be replaced with (ifn − ifn2) (Ψf(n+1)1 − Ψfn1), namely (ifn/m) (Ψf(n+1)1 − Ψfn1). Thus,
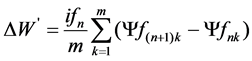 . (11)
. (11)
Replaced with Equation (2), the analytical solution of Tem is given as
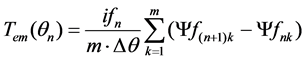 . (12)
. (12)
3.2. Simulation Analysis
To get the solution of Equation (12), it is necessary to get the information of every rotor position and corres-

Figure 4. ΔW’ for linear formula. (a) ifn < ifn+1; (b) ifn > ifn+1.
Figure 5. Integral calculation of ΔW’.
Table 2. Expressions and applications of Tem with no load.
ponding Ψf with every current point. The combined simulation of Maxwell and Simplorer is adopted. The simulation condition is shown as follows: motor operates with no load, voltage exciting with 20 V (internal resistor 2 Ω, exciting current 10 A), rotate speed is 60 rpm, 10 uH inductance measured from prototype. Simulation cycle is 4 with 120 sampling points in each cycle. Δθ = 45˚/120 = 0.375˚ since the mechanical angle is 45˚ in each cycle. Figure 6 shows the combined simulation of Maxwell and Simplorer.
In order to make sure that the exciting current changes from 0 to ifn evenly at certain position θn, it is necessary to input the rotate speed and exciting current according to the table. The Data_If in Figure 6 refers to the exciting current, which shows the even current in any position. The Data_ω refers to rotate speed table which
Figure 6. Simulation circuit with Maxwell and Simplorer.
shows the rotate speed impact signal. Only when exciting current changes to the end value that the rotate speed gives out a value, which makes the rotor changes Δθ. At other time, the rotate speed is zero.
After the simulation, the relationship between Tem and rotor position angle can be derived from the calculation results by using Equation (12). Figure 7 shows the results of calculated torque and simulation torque using Finite Element (FEM).
From the result in Figure 7 it has a good match between calculation and simulation, with the max error of 4.91%. All these result verifies that correctness of the nonlinear formula with no load.
4. Experiment Verification
4.1. Experimental Result
The 12/8 salient prototype WFDSG in lab is used to test the torque. The generator is controlled with Siemens servo controller,
Figure 9(a) shows the tested torque and three-phase waveforms with no load at the speed of 60 rpm. Figure 9(b) shows the simulation results. Comparing Figure 9(a) with Figure 9(b), the test result and simulation result match each other well:
(1) The test torque signal also matches the simulation at the frequency of 24 Hz (3pn/60).
(2) The zero point of Tem matches the cross-zero of the phase voltage (point a corresponds point b in Figure 9(a) and point A corresponds point B in Figure 9(b)).
(3) The max point in Tem correspond the positive natural commutation point in phase voltage (point c corresponds point d in Figure 9(a) and point C corresponds point D in Figure 9(b)).
(4) The min point in Tem correspond the negative natural commutation point in phase voltage (point e corresponds point f in Figure 9(a) and point E corresponds point F in Figure 9(b)).
However, there is still some difference between the simulation and test results, as shown in Table 3. The torque pulse peak to peak value is smaller than that of the simulation result with 8.8% error. The average Tem is zero while the test result is −1.61 Nm. Besides, the waveform of the simulation is much smooth than that of test result, where there is a lot of high frequency harmonic.
Figure 7. Comparison of calculation torque and simulation torque.
Figure 8. Experiment platform of WFDSG.

Figure 9. Experiment and simulation waveforms of WFDSG. (a) Experiment waveforms; (b) Simulation waveforms.
Table 3. Comparison of experiment data and simulation data.
4.2. Error Analysis
Based on the simulation and test result, the difference is mainly due to the following items:
(1) Theoretical error
The torque of simulation is Tem. However, in the experiment, the torque is input torque, which is not only the Tem but also contains other kinds of torque:

where Jdω/dt refers to the flywheel torque, J refers to the rotary inertia, ω refers to the rotor angular speed, contributing to the high frequency harmonic in every cycle. Bω refers to the friction torque, B is equivalent to the mechanical friction of motor bearings, rotor and air friction and heat loss, together with the friction coefficient. If the rotate speed of the motor is constant, then the average value of Bω is a constant too. That’s why the average torque in the test is negative.
(2) Model error
The FEM model in the simulation can’t simulate the real condition totally. Only based on the following conditions then FEM can be applied.
1) Punching isotropic core material, and the magnetization curve is a single value, namely ignoring hysteresis.
2) External motor magnetic field is negligible.
3) Using Cartesian coordinates, which is a two-dimensional field analysis.
5. Conclusions
(1) This paper compares the theoretical difference in nonlinear formula, approximate nonlinear formula and linear formula, emphasizing the correctness of nonlinear formula.
(2) Get the analytical solution of Tem nonlinear formula by adopting virtual displacement method. Verify the correctness by the combined simulation of Maxwell and Simplorer.
(3) The simulation result and test result match each other well by WFDSG torque prototype under no load condition. Explain the difference between simulation and test.
(4) Get the analytical Tem solution of WFDSG under no load condition, which offers a base for further analysis on Tem analytical solution with load.
Cite this paper
Fan Yang,Jin Ma,Haoji Xu, (2015) Study on Torque Ripple of Wound-Field Doubly Salient Generator with No Load. World Journal of Engineering and Technology,03,111-118. doi: 10.4236/wjet.2015.33C017
References
- 1. Zheng, Y., Sun, H.X., Dong, Y. and Wang, W. (2007) Torque Ripple Minimization with Current Oriented Method of Switched Reluctance Motor. Proceedings of International Conference on Electrical Machines and Systems, Seoul, 8-11 October 2007, 1640-1644.
- 2. Kalaivani, L., Marimuthu, N.S. and Subburaj, P. (2011) Intelligent Control for Tor-que-Ripple Minimization in Switched Reluctance Motor. 1st International Conference on Electrical Energy Systems, Newport, 3-5 January 2011, 182-186. http://dx.doi.org/10.1109/icees.2011.5725325
- 3. Zhang, L., Zhou, B. and Zhang, Y.S. (2010) Analysis and Suppression of Torque Ripple for Doubly Salient Electro- Magnetic Motor. Proceeding of the CSEE, 30, 83-89.
- 4. Cheng, M., Chau, K.T. and Chan, C.C. (2001) Static Characteristics of a New Doubly Salient Permanent Magnet Motor. IEEE Transactions on Energy Conversion, 16, 20-25. http://dx.doi.org/10.1109/60.911398
- 5. Ma, C.S. and Zhou, B. (2007) A Novel Control Strategy of Turn-On Angle and Turn-Off Angle for Doubly Salient Permanent Motor. Proceeding of the CSEE, 27, 68-73.










