World Journal of Engineering and Technology
Vol.03 No.03(2015), Article ID:60486,6 pages
10.4236/wjet.2015.33C011
Robust Design of Mixing Static and Dynamic Multiple Quality Characteristics
Ful-Chiang Wu
Department of Hotel Management, Vanung University, Chung-Li, Tao-Yuan, Taiwan, China
Email: shogo@vnu.edu.tw


Received 31 July 2015; accepted 15 October 2015; published 22 October 2015

ABSTRACT
Increased market competition means that quality, cost and delivery time are crucial elements of modern production techniques. Taguchi’s robust design is the most powerful method available for reducing product cost, improving quality, and simultaneously reducing development time. Robust design aims to reduce the impact of noise on the product or process quality and leads to greater customer satisfaction and higher operational performance. The objective of robust design is to minimize the total quality loss in products or processes. The PQL model proposed by this paper simultaneously optimizes the static and dynamic problems by minimizing the total quality loss. Using the proposed PQL model and steps for optimization, the method addresses complex parameter design, which varies with the properties and objectives of the experimental data, to improve the product quality. The example of an electron beam surface hardening process is provided to demonstrate the implementation and usefulness of the proposed method.
Keywords:
Robust Design, Quality Characteristic, Quality Loss Function, SN Ratio, PQL

1. Introduction
Quality, cost and delivery time are the main production elements of the modern products due to the stringent market competitiveness. Taguchi’s robust design [1] is the most powerful method available to reduce product cost, improve quality, and simultaneously reduce development interval. The Taguchi method has been widely applied to optimize the industrial parameter design including static and dynamic problems. The static problem is defined so that the desired output of system has a fixed target. In the dynamic problem, the desired output of the system depends on the signal factor setting, that is, the dynamic system is the one without a single target but a response, which is a function of a signal. The optimization involves determining the best control factor levels so that the output is at the target or desired value to minimize the total quality loss.
Many publications have addressed multiple static quality characteristics problems (see Derringer and Suich [2], Elsayed and Chen [3], Khuri and Conlon [4], Jean and Tzeng [5] [6]). Several researchers have studied the problem of robust design concerning the dynamic problems (see Lesperance and Park [7], Nair, Taam and Ye [8], Wu [9], Jean and Tzeng [10], Jean [11]). However, few studies have been concerned with optimizing the robust design involving static and dynamic quality characteristics.
In this paper, we propose a PQL index to convert the multiple quality characteristics into a single characteristic problem by minimizing the total PQL value to obtain the optimal parameter conditions.
2. Quality Loss Function and SN Ratio
The quality characteristics can be divided three types according to the target of problem: (1) the smaller-the- better (STB) type for static system; (2) the larger-the-better (LTB) type for static system; and (3) the nominal- the-best (NTB) type, which can be classified as static system and dynamic system.
Taguchi [1] proposed the SN ratio (h) as the quality evaluation based on the quadratic average quality loss function . Taguchi defined the SN ratio as
. Taguchi defined the SN ratio as
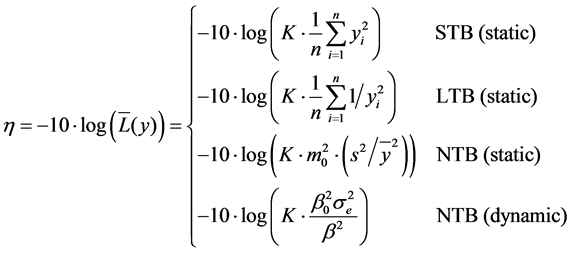 (1)
(1)
where
K = the loss coefficient (constant)
y = a measurable statistic of quality characteristic
m0 = the target value for static NTB quality characteristic
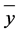 = the sample mean of n units
= the sample mean of n units
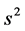 = the sample variance of n units
= the sample variance of n units
b0 = the slope of ideal function for dynamic NTB quality characteristic
b = the estimated slope of regression for dynamic NTB quality characteristic
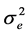 = the error variance of regression for dynamic NTB quality characteristic
= the error variance of regression for dynamic NTB quality characteristic
The loss coefficient K, m0 and b
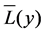 are generally ignored because they have no effect on the optimization for a single quality characteristic. In multiple quality characteristics problems, the loss coefficient K plays a major role in optimal parameter settings to make trade-offs among characteristics. Since log is a monotone function, minimizing
are generally ignored because they have no effect on the optimization for a single quality characteristic. In multiple quality characteristics problems, the loss coefficient K plays a major role in optimal parameter settings to make trade-offs among characteristics. Since log is a monotone function, minimizing 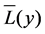 is equivalent to maximizing h.
is equivalent to maximizing h.
3. Robust Design Model
The analysis of means (ANOM) is used to determine the optimal factor levels in robust design. The ANOM is used for estimating the main effects of each parameter, and the effect of a factor level is the deviation it causes from the overall mean response. Let 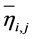 be the average SN ratio value for the jth level of factor Xi,
be the average SN ratio value for the jth level of factor Xi, 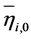 be average SN ratio value for the starting conditions of Xi and
be average SN ratio value for the starting conditions of Xi and 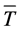 be the total average SN ratio value. The effect of the jth level of Xi is defined as
be the total average SN ratio value. The effect of the jth level of Xi is defined as
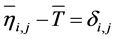 (2)
(2)
Suppose there are q control factors, 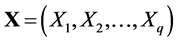 , in the experiment for a single quality characteristic. The effects of SN ratios for some parameter conditions and starting conditions are (
, in the experiment for a single quality characteristic. The effects of SN ratios for some parameter conditions and starting conditions are (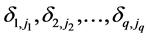 ) and (
) and (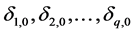 ), respectively. Then, the estimated SN ratio values are presented as follows respectively.
), respectively. Then, the estimated SN ratio values are presented as follows respectively.
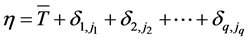 (3)
(3)
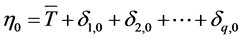 (4)
(4)
The relationship between (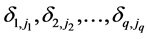 ) and (
) and (
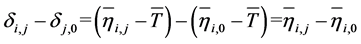
Let L be the quality loss for the some parameter conditions and L0 be the quality loss for the starting conditions. The ratio of L to L0 (proportion of quality loss, PQL) is defined as.

Consider the effect of each factor in 
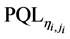

Therefore, the optimal parameter conditions 

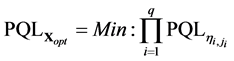

Suppose a product or process has p quality characteristics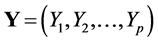




If the real quality loss of starting conditions, 
quality loss Lj of quality characteristic Yj as the base to find the proportion of quality loss Li of quality characteristic Yi to Yj. Hence, the proportion 
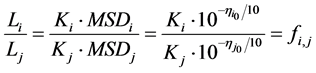
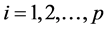
Therefore, Equation (10) can be rewritten as
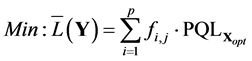
To solve the multiple quality characteristics problems, an optimization procedure is proposed as follows.
Step 1. Compute the SN ratio for each quality characteristic and then calculate the main effect of factors for each quality characteristic.
Step 2. Estimate the average SN ratio (h0) under the starting conditions for each quality characteristic.
Step 3. Transform the SN ratios into PQL for each quality characteristic.
Step 4. Estimate the quality loss of starting conditions for each quality characteristic and then program a search module by EXCEL VBA to obtain the optimal parameter conditions.
4. Implementation
The case used is that described by Jean and Tzeng [5] [6] [10], Jean [11]. They studied the static or dynamic problem in the electron beam surface hardening process. We use the published process conditions and experimental data to demonstrate the proposed method, which can simultaneously optimize the static and dynamic problems.
High energy electron beam is a unique tool for case hardening. The control factors are substrate matrix (factor A), travel speed (factor B), accelerating voltage (factor C), electrical current (factor D), melted width (factor E), beam oscillation (factor F) and post-heat treatment temperature (factor G). The signal factor is electron beam scanning width (factor M). The levels of control and signal factors are listed in Table 1.
There are two quality characteristics for the process. The first is wear volume (STB type) and the second is microhardness (dynamic type). A L18 orthogonal array is built and the assignment of controls, signal factor, experimental data and the computed SN ratios (h) for all quality characteristics are shown in Table 2.
The main effect of factors and PQL values for each quality characteristic are shown in Table 3, respectively. Suppose that the quality loss of starting levels for wear volume and microhardness are L1 and L2 respectively. The region of 
Table 1. Levels of control and signal factors for electron beam surface hardening process.
a. Starting levels are identified by underscore.
Table 2. Experimental data.
Table 3. Summary of factor effects for wear volume and microhardness (h and PQL).
a. Optimal parameter levels for each characteristic are identified by boldface type.
Table 4. The region of 
5. Conclusion
Robust design is used to determine the optimal levels for the control factors in a product or process so that the quality loss is minimized. A real problem in a product or process usually has multiple quality characteristics. This paper presents an effective method based on Taguchi’s quality loss function and SN ratio to simultaneously optimize the robust design involving both static and dynamic quality characteristics. Using the PQL transformed from the factor effects of SN ratios as the quality evaluation, we can convert the static and dynamic multiple quality characteristics into a single characteristic problem to obtain the optimal parameter conditions by minimizing the total PQL value. The implementation and effectiveness of the proposed approach is illustrated through case study.
Acknowledgements
This research was financially supported by Ministry of Science and Technology (Republic of China) under Contract MOST 104-2221-E-238-003.
Cite this paper
Ful-Chiang Wu, (2015) Robust Design of Mixing Static and Dynamic Multiple Quality Characteristics. World Journal of Engineering and Technology,03,72-77. doi: 10.4236/wjet.2015.33C011
References
- 1. Taguchi, G. (1991) System of Experimental Design: Vol. 1 and Vol. 2. American Suppliers Institute, Dear-born.
- 2. Derringer, G. and Suich, R. (1980) Simultaneous Optimization of Several Response Variables. Journal of Quality Technology, 12, 214-219.
- 3. Elsayed, E.A. and Chen, A. (1993) Optimal Levels of Process Parameters for Products with Multiple Characteristics. International Journal of Production Research, 31, 1117-1132. http://dx.doi.org/10.1080/00207549308956778
- 4. Khuri, A.I. and Conlon, M. (1981) Simultaneous Optimization of Multiple Responses Represented by Polynomial Regression Functions. Technometrics, 23, 363-375. http://dx.doi.org/10.2307/1268226
- 5. Jean, M.D. and Tzeng, Y.F. (2003) Use of Taguchi Methods and Multiple Regression Analysis for Optimal Process Development of High Energy Electron Beam Case Hardening of Cast Iron. Surface Engineering, 19, 150-156. http://dx.doi.org/10.1179/026708403225002496
- 6. Jean, M.D. and Tzeng, Y.F. (2004) Optimisation of Elec-tron-beam Surface Hardening of Cast Iron for High Wear Resistance Using Taguchi Method. International Journal of Advanced Manufacturing Technology, 24, 190-198. http://dx.doi.org/10.1007/s00170-002-1481-1
- 7. Lesperance, M.L. and Park, S.M. (2003) GLMs for the Analysis of Robust Designs with Dynamic Characteristics. Journal of Quality Technology, 35, 253-263.
- 8. Nair, V.N., Taam, W. and Ye, K.Q. (2002) Analysis of Functional Responses from Robust Design Studies. Journal of Quality Technology, 34, 355-370.
- 9. Wu, F.-C. (2007) Sequential Optimization of Parameter and Tolerance Design for Multiple Dynamic Quality Characteristics. International Journal of Production Research, 45, 2939-2954. http://dx.doi.org/10.1080/00207540600690719
- 10. Jean, M.D. and Tzeng, Y.F. (2003) Robust Design of Electron Beam Surface Hardening Process Using Taguchi Dynamic Experiment. Journal of Materials Science and Engineering, 35, 207-216.
- 11. Jean, M.D. (2004) Characteristic Optimisation of Dynamic Process Parameters in Rapid Solidified Treatment. Science and Technology of Welding and Joining, 9, 221-228. http://dx.doi.org/10.1179/136217104225012193


