World Journal of Mechanics, 2015, 5, 165-177
Published Online September 2015 in SciRes. http://www.scirp.org/journal/wjm
http://dx.doi.org/10.4236/wjm.2015.59017
How to cite this paper: Sharada, K. and Shankar, B. (2015) MHD Mixed Convection Flow of a Casson Fluid over an Exponen-
tially Stretching Surface with the Effects of Soret, Dufour, Thermal Radiation and Chemical Reaction. World Journal of Me-
chanics, 5, 165-177. http://dx.doi.org/10.4236/wjm.2015.59017
MHD Mixed Convection Flow of a Casson
Fluid over an Exponentially Stretching
Surface with the Effects of Soret, Dufour,
Thermal Radiation and Chemical Reaction
Kankanala Sharada, Bandari Shankar
Department of Mathematics, Osmania University, Hyd erabad , India
Received 29 July 2015; accepted 26 September 2015; published 29 September 2015
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Abstract
The present study deals with MHD (magneto hydrodynamics) mixed convection flow of a Casson
fluid over an exponentially stretching sheet with the effects of Soret and Dufour, thermal radiation,
chemical reaction. The governing partial differential equations are converted into ordinary dif-
ferential equations by using similarity transformations. These equations are then solved numeri-
cally by applying finite difference scheme known as the Keller Box method. The effects of various
parameters on velocity, temperature and concentration profiles are presented graphically to in-
terpret and the results are discussed.
Keywords
Casson Fluid, Magneto Hydrodynamics, Mixed Convection, Exponentially Stretching Surface, Soret
and Dufour Effects, Thermal Radiation, Chemical Reaction
1. Introduction
The study of magnet o hy drodyna mics, boundary layer flow with heat and mass transfer from a stretching surface
has many applications in industrial and engineering fields. Magnetic fields can be used to manage thermal en-
ergy in flowing electr ically conducting polymers (Garnier [1]). After the pion eering studies of Sakiadas [2] and
Crane [3], several researchers further investigate the problem of stretching sheet boundary layer flow to obtain
thermal and kinematic behaviour by considering the various types of stretching velocity. Magyari and Keller [4]
examine the similarity solutions of thermal boundary layer and flow over an exponentially stretching surface

K. Sharada, B. Shankar
166
with an exponential temperature distribution. Numerical solution of boundary layer flow over an exponentially
stretching sheet includ ing thermal radiatio n is inv estigated by Bidin and Nazar [5], and analytical stud y is inves-
tigated by Sajid and Hayat [6].
Casson fluid is one type of fluid model for non-Newtonian flu id, which has significant applications in poly-
mer processing industries and biomechanics. Casson fluid can be defined as a shear thinning liquid which is
presumed to have an infinite viscosity at zero rate of shear and a yield stress under which no flow occurs and
zero viscosity at an infinite rate of shear. Casson fluid model is used in many foodstuffs and biological materials,
especially blood. It describes the steady shear stress, shear rate behaviour of blood. Merill et al. [7] and Mc
Donald [8] investigate the b ehaviour of blood. Nadeem et al. [9] investigate the magneto hydrodynamic bound-
ary layer flow of Casson fluid over exponentially permeable shrinking sheet. Casson fluid over an unsteady
stretching sur face is analyzed by Mukhopadhyay [10]. The application of the minimal energy phenomenon to a
Casson fluid is studied by John L. McGregor [11]. A similarity solution technique for mixed convection heat
transfer from an exponen tially stretching surface with the eff ect of viscous dissipation is investigated by Par tha
et al. [12]. Recently Dual pal [13] studies mixed convection heat transfer in the boundary layers over an expo-
nentially stretching surface including magnetic field. The effects on mixed free forced convective and mass
transfer steady, laminar boundary layer flow over a vertical plate with temperatur e dependent viscosity are pre-
sented by Kafoussias and Williams [14].
The mass flux created by temperature gradient is known as thermal diffusion (Soret) effect. The energy flux
caused by concentration differences is known as diffusion thermo (Dufour) effect. The Soret effect has been
utilized for medium molecular weight (eg. N2 and air) and isotope separation. These effects have several appli-
cations in engineering problems. Here a survey conducted by Dursunkaya and Worek [15] on Soret and Dufour
effects in transient and steady natural convection from a vertical surface. The combined effects of thermal diffu-
sion and diffusion thermo over stretching surface with free convective heat and mass transfer are investigated by
Afify [16]. T. Hayat [17] describes the effects of Soret and Dufour on magneto hydrodynamic flow of Casson
fluid. Alam and Rahman [18] study the Dufour and Soret effects on mixed convect ion fl ow wi th var iable suction.
Several researchers have studied the effects of thermal radiation, and these include that Pramanik [19] inves-
tigates Casson fluid flow and heat transfer over an exponentially stretching surface in the presence of thermal
radiation and porous medium. Numerical analysis of magneto hydrodynamic stagnation point flow of a Casson
fluid includes thermal radiation discussed by Shateyi and Marewo [20]. Anur Ishak [21] present the magneto
hydrodynamic boundary layer flow over an exponentially stretching sheet with the effect of radiation. Swathi
Mukhopadhyay [22] investigate Casson fluid flow and heat transfer on an unsteady stretching surface subjected
to suction/blowing with the effect of thermal radiation. Recently effects of mass transfer on magneto hydrody-
namic flow of Casson fluid with che mical reactio n are studied by S.A. Shehzad and T. Hayat [23].
This paper provides the solution to the problem of fluid flow, heat and mass transfer of a Casson fluid over an
exponentially stretching surface by considering the effect of Soret and D ufo ur, thermal radiatio n, chemical reac-
tion by adopting the Keller Box method.
2. Mathematical Formulation
Consider two-dimensi onal ste ady, lamina r, incompressi ble MHD flow of a C as son flui d over a vert i cal exponential
surface stretching with velocity
()
ex
L
w
Ux a =
, temperature distribution
()
w
Tx
and concentration distribution
( )
w
Cx
moving through a fluid of constant temperature
T
∞
and concentration
C
∞
as shown in Figure 1. The
x-axis is oriented about the vertical surface in the upward direction and y-axis is normal to it. A magnetic field is
applied in the direction perpendicular to the stretching surface. The magnetic Reynolds number is taken to be
small enough such that the induced magnetic field is negligible. The rheological equation of state for an iso-
tropic and incompressible f low of a Casson fluid can be written as:
2
2
y
ij bij
Pe
τµ π

= +


when
c
ππ >
(1)
2
2
y
ij bij
c
Pe
τµ π

= + 


when
c
ππ <
(2)

K. Sharada, B. Shankar
167
Figure 1. Physical model and coordinate system.
y
P
is known as yield stress of the fluid, mathematically expressed as
2
b
y
P
µπ
β
=
,
b
µ
is known as plastic
dynamic viscosity of the non Newtonian fluid, π is the product of the component of deformation rate with itself
(i.e.
ij ij
ee π =
) and
ij
τ
is the (i, j)th component of the stress tensor.
Considering u, v as velocity components in the directions of x and y respectively in the flow field. The gov-
erning equations of continuity, momentum, energy and concentration are given by
0
uv
xy
∂∂
+=
∂∂
(3 )
() ()
( )
22
*
2
1
1
TC
u uuBu
u vgTTCC
xy y
σ
υ ββ
βρ
∞∞

∂∂ ∂
+= ++−+−−

∂∂ ∂

(4)
2
22
22
11
1
rT
p pps
q Dk TT TuC
uv
xycy CyCC yy
ν
αρβ
 ∂ ∂∂ ∂∂∂
+=−+ ++
 
∂∂∂ ∂ ∂∂
 
(5)
( )
22
22
T
m
DK
CC CT
uvDkC C
xy T yy
∞
∂∂ ∂∂
+ =+−−
∂∂ ∂∂
. (6)
where
ρ
is the density of the fluid,
σ
is the electrical conductivity,
υ
is the kinematic viscosity, B is the
magnetic induction, α is the thermal diffusivity, D is the solutal diffusivity of the medium,
T
β
and
C
β
are the
coefficient of thermal and solutal expansions, μ is the dynamic co-efficient of viscosity,
p
C
and
s
C
are the
specific heat capacity and concentration susceptibility,
m
T
is the mean fluid temperature,
T
K
is the thermal
diffusion ratio, γ is the chemical reaction parameter and
2
b cy
P βµ π =
is the Casson parameter.
The boun da ry c ondition s c on s i de r ed are defined as:
( ) ( )
2
0
e ,0,e
xx
LL
ww
uU xavTTTTT
∞∞
=== ==+−
( )
2
0
e
x
L
w
CCCC C
∞∞
==+−
at
0 y=
(7)
, ,0uTTC C
∞∞
=→→
as
y→∞
(8)
where subscripts w and
∞
indicate that conditions at the wall and at the external(outer) edge of the boundary
layer respectively and
( )
w
Ux
is the stretching velocity,
( )
w
Tx
and
( )
w
Cx
are the exponential temperature
and concentration distr ibution respectively.
In above conditions “a” is velocity parameter of the stretching surface,
0
T
is temperature distribution pa-

K. Sharada, B. Shankar
168
rameter,
0
C
is the parameter of the concentration distribution in the stretching surfac e.
We introduce stream function ψ as
Ψ
uy
∂
=∂
,
vx
ψ ∂
= −∂
and defi ne va riables.
() ()( )
22
e ,e,e
22
x xx
L LL
aa
u afyvff
LL
υ
ηηηη η
υ
′′
===−+ 

( ) ( ) ( )() ( ) ( )
22
00
,e ,,e
xx
LL
T xyTTTCxyCCC θη φη
∞∞∞ ∞
=+−=+ −
By using the Rosseland approximation for radiative heat flux,
r
q
is define d a s:
*4
*
4
3
r
T
qy
Kk
σ ∂
= −∂
(9)
where
*
σ
is the Stephen Boltzman constant and
*
K
is the mean absorption coeff icient. Sin ce the te mperature
differences within the flow field are assumed to be small, and then we linearize and expand
4
T
into the Taylor
series about
T
∞
, which after neglecting higher order forms take the form.
43 4
43TTT T
∞∞
≅−
To obtain similarity solutions, we assumed that the magnetic field is of the form
( )
0
e
x
L
Bx B=
where
0
B
is
the constant magnetic field and
( )
0
e
x
L
Kx K=
is the exponential reaction,
0
K
is constant.
With the help of above similarity transformations the governing equations are transformed in to
( )()
3
22
1
12 2e0
X
f fffNMf λ θφ
β
−

′′′ ′′′′
++−++− =


(10)
( )( )
32
2
41
1 10
3
X
f
NrPr ffPrEcefPrD θ θθφ
β


′′′ ′′′′′
++−+++ =


 
(11)
()
0Sc ffScSrSc φφ φθγφ
′′′ ′′′
+−+− =
(12)
The correspondin g bo undary condition s are
() ()()()
0 1,001, 0101 : ,ff θη φ
′
=== = =
( )( )( )
:0,0, 0f ηθφ
′
→∞ ∞=∞=∞=
where
x
XL =
is the X-location, observing Equations (10), (11) in MHD mixed convection due to Casson fluid,
the velocity and temperature profiles are not similar because the x coordinate cannot be deleted from these equa
tions. It is hard to proceed in this case. To reduce the difficulty of analysis, it was considered
x
XL =
to find
local similarity solutions for the governing equations. Now one can study the effects of different parameters on
various profiles at any given X-location.
2
0
2BL
Ma
σ
ρ
=
is the magnetic parameter,
2
Gr
Re
λ =
is the mixed convection parameter,
aL
Re
ν
=
is the
Reynolds number,
( )
*3
0
²
T
g TTL
Gr
β
ν
∞
−
=
is the Grashoff number,
( )
( )
0
0
c
T
CC
NTT
β
β
∞
∞
−
=−
is the Buoyancy ratio,
Pr
ν
α
=
is the Prandtl number,
()
0
²
p
a
Ec CT T
∞
=−
is the Eckert number,
*3
*
4
3
T
Nr kk
σ
∞
=
is the Thermal radia-
tion parameter,
( )
( )
0
0
T
fsp
DK CC
DCCTT
ν
∞
∞
−
=−
is the Dufour number,
( )
()
0
0
T
m
DK TT
Sr TC C
ν
∞
∞
−
=−
is the Soret number,
Sc D
ν
=
is the Schmidt number,
0
KL
a
γ =
is the chemical reaction parameter.

K. Sharada, B. Shankar
169
The wall shear stress, heat and mass trans fer coefficients with constant density are given by
0
2
y
wb
y
Pu
y
τµ π
=



 ∂
= +
∂

,
0
w
y
T
qk
y
=
 ∂
= −
∂

and
0
m
y
C
qD
y
=
 ∂
= −
∂

where k is the thermal conductivity. The
dimensionless form of skin friction
2
2w
f
CU
τ
ρ
∗
=
. Where
*
U
is the characteristic velocity, the local Nusselt
number
( )
w
xw
xq
Nu kT T
∞
=−
, and local Sherwood number
()
w
xw
xq
Sh DC C
∞
=−
are given by
( )( )
21 4
1 0,10
32
x
xx
x
Re X
X
Cff NuNr
Re
θ
β
 
′′ ′
= +=−+
 


and
( )
0.
2
x
x
Re
Sh φ
′
= −
3. Method of Solution
The governing equations with boundary equations are solved numerically by using finite difference scheme
known as Keller Box method which is described by Cebeci and Bradshaw [24]. This method involves the fol-
lowing steps:
Step 1: Reducing higher order ODEs (systems of ODES) in to systems of first order ODEs;
Step 2: Writing the systems of first order ODEs into difference equations using central diffe rence scheme ;
Step 3: Linearizing the difference equations using Newton’s method and writing it in vector fo rm;
Step 4: Solving the system of equations using block elimination method.
4. Numerical Discussions
To solve the above differential equations numerically, we adopt Matlab software. In this process the step size,
0.01 η ∆=
is used to obtain numerical solution with five decimal place accuracy as the criterion of convergence.
Table 1 shows that the comparison between wall temperature gradient
()
0 θ
′
calculated by the present method
and of Magyari and Keller for λ = X = Df = Nr = Sr = γ = N = M = Sc = Ec = 0 and
β →∞
. The numerical
vales of
( )
1
10f
β

′′
+


,
( )
0 θ
′
−
, and
( )
0 φ
′
−
for the various values of λ, X, Df , Nr, Sr, γ, β are shown in Ta-
ble 2.
5. Results and Discussion
In the present study, the following values are adopted for the numerical computations N = 0.5, Df = 0.03, Sr =
0.5, λ = 1.0, Pr = 1.0, M = 1.0, Sc = 0.22 , X = 0.5, γ = 0.1 , β = 0.5. Thes e values are used throug hout the calcu la-
tions unless otherwise mentioned.
Figure 2 shows that the non-dimensional velocity profile for different values of the mixed convection pa-
rameter λ. We have observed the results for both aiding flow and apposing flow. It illustrates that the dimen-
sionless velocity increases, as the value of λ increases. As λ increases, the buoyancy effects increase and hence
the fluid flow accelerates. In the case of mixed convection, temperature is low for aiding flow and more for
Table 1. Comparison of results for
( )
0 θ ′ −
with previous published work.
Pr Magyari and Keller [4] Present
0.5
1.0
3.0
5.0
8.0
10.0
−0.59434
−0.95478
−1.86908
−2.50014
−3.24213
−3.66038
−0.5946
−0.9548
−1.8691
−2.5002
−3.2423
−3.6606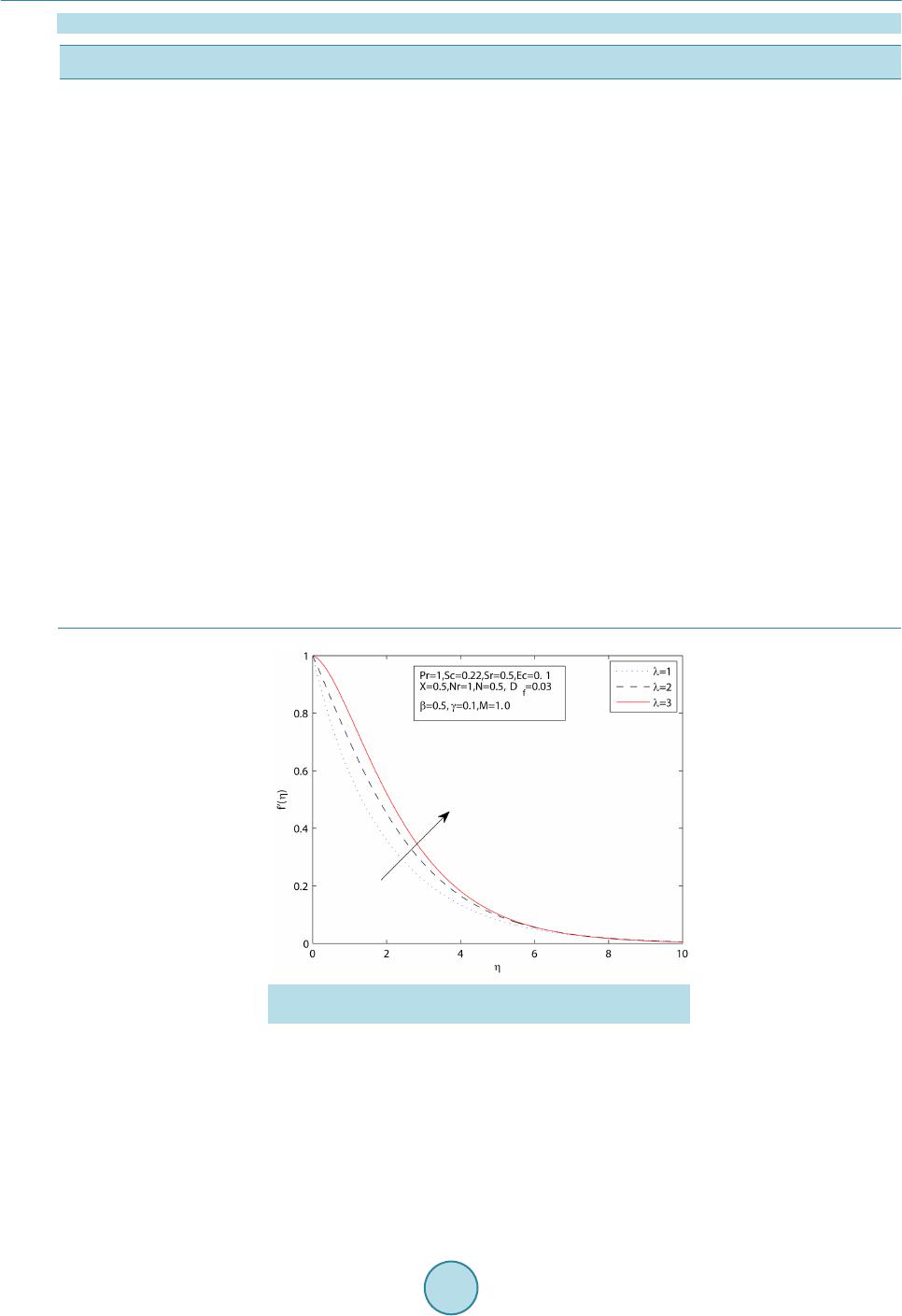

K. Sharada, B. Shankar
170
Table 2. Effects of s k i n f r icti o n co ef f icien t, h eat and mass tr an sfer coefficients fo r various values o f λ, X, Df , Nr, Sr, γ and β.
Λ X Nr Sr


γ Β (1 + 1/β)"(0) −θ'(0) −Ф'(0)
1.0
2.0
3.0
0.5
0.5
0.5
1.0
1.0
1.0
0.5
0.5
0.5
0.03
0.03
0.03
0.1
0.1
0.1
0.5
0.5
0.5
−1.9167
−1.1259
−0.3918
0.6505
0.7017
0.7383
0.4246
0.4560
0.4797
1.0
1.0
1.0
0.2
1.0
2.0
1.0
1.0
1.0
0.5
0.5
0.5
0.03
0.03
0.03
0.1
0.1
0.1
0.5
0.5
0.5
−1.4607
−2.3684
−2.7091
0.6870
0.5841
0.3124
0.4431
0.4044
0.4054
1.0
1.0
1.0
0.5
0.5
0.5
1.5
3.0
4.6
0.5
0.5
0.5
0.03
0.03
0.03
0.1
0.1
0.1
0.5
0.5
0.5
−1.8828
−1.8174
−1.7766
0.5637
0.4204
0.3429
0.4371
0.4593
0.4722
1.0
1.0
1.0
0.5
0.5
0.5
1.0
1.0
1.0
1.0
3.0
5.0
0.03
0.03
0.03
0.1
0.1
0.1
0.5
0.5
0.5
−1.9071
−1.8687
−1.8309
0.6527
0.6612
0.6692
0.3779
0.1894
−0.0019
1.0
1.0
1.0
0.5
0.5
0.5
1.0
1.0
1.0
0.5
0.5
0.5
1.0
2.0
3.0
0.1
0.1
0.1
0.5
0.5
0.5
−1.8774
−1.8372
−1.7967
0.5596
0.4601
0.3535
0.4387
0.4530
0.4675
1.0
1.0
1.0
0.5
0.5
0.5
1.0
1.0
1.0
0.5
0.5
0.5
0.03
0.03
0.03
0.15
0.25
0.35
0.5
0.5
0.5
−1.9203
−1.9266
−1.9326
0.6496
0.6480
0.6466
0.4394
0.4670
0.4927
1.0
1.0
1.0
0.5
0.5
0.5
1.0
1.0
1.0
0.5
0.5
0.5
0.03
0.03
0.03
0.1
0.1
0.1
0.8
1.0
1.5
−1.6085
−1.4976
−1.3415
0.6370
0.6315
0.6233
0.4171
0.4143
0.4101
Figure 2. Velocity profiles for various values of mixed con-
vection parameter λ.
opposing flow. As λ increases, the convection cooling effect increases and therefore temperature decreases.
Figure 3, Figure 4 reveal that the dimensionless temperature and concentration reduces with increase of λ.
Figure 5 depicts the effects of Casson parameter β on dimensionless velocity profiles for impermeable
stretching surface. The velocity is found to decrease with the increasing Casson parameter β. Figure 6, Figure 7
present the temperature and concentration profiles for Casson parameter β. It shows that the both temperature
and concentration profiles decreasing with increasing of β. Figure 8 illustrates the velocity profile for different
values of the magnetic parameter M. The presence of magnetic field reduces the momentum boundary layer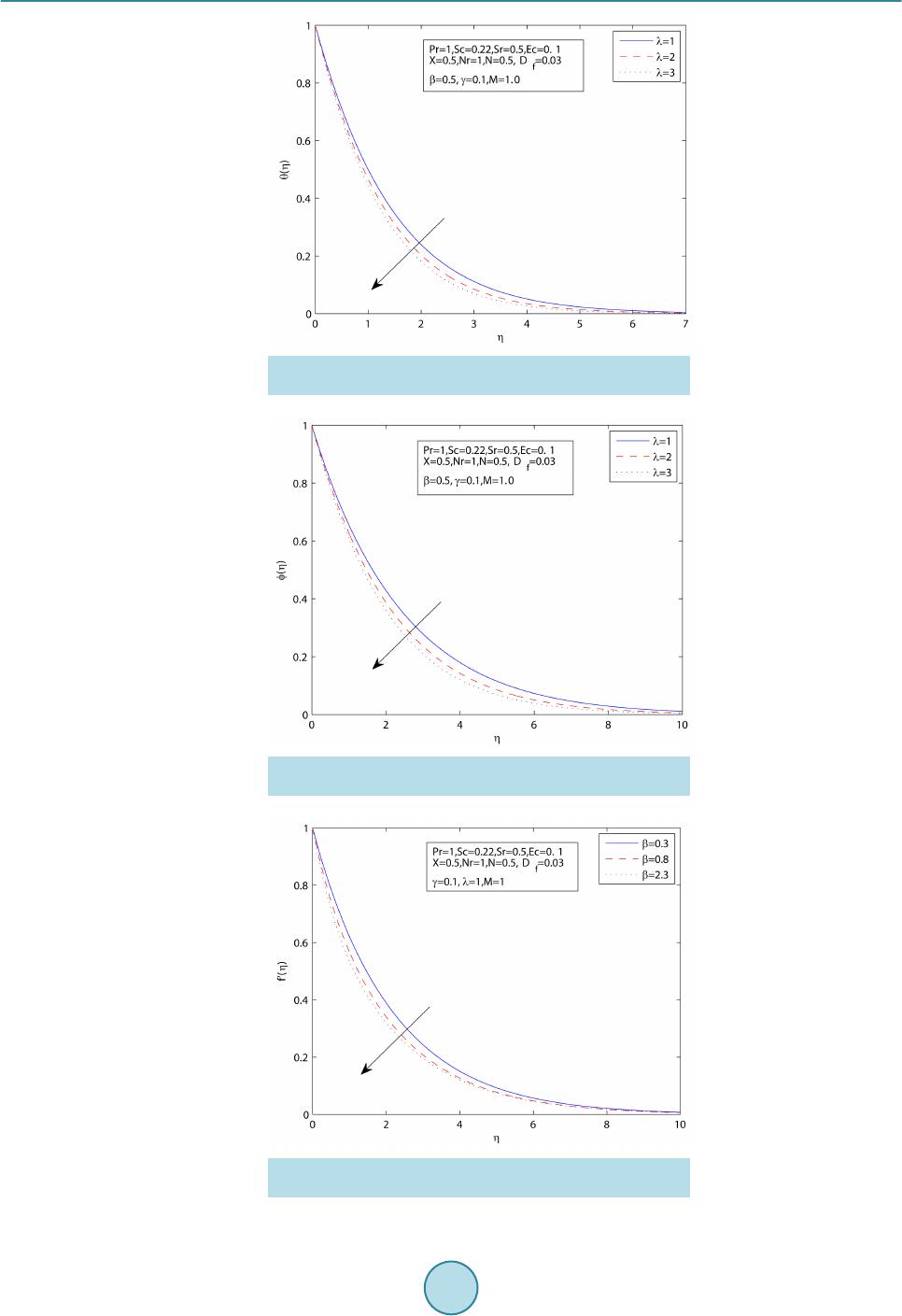

K. Sharada, B. Shankar
171
Figure 3. Temperature profiles for various values of mixed
convection parameter λ.
Figure 4. Concentration profiles for various values of mixed
convection parameter λ.
Figure 5. Velocity profiles for various values of Casson pa-
rameter β.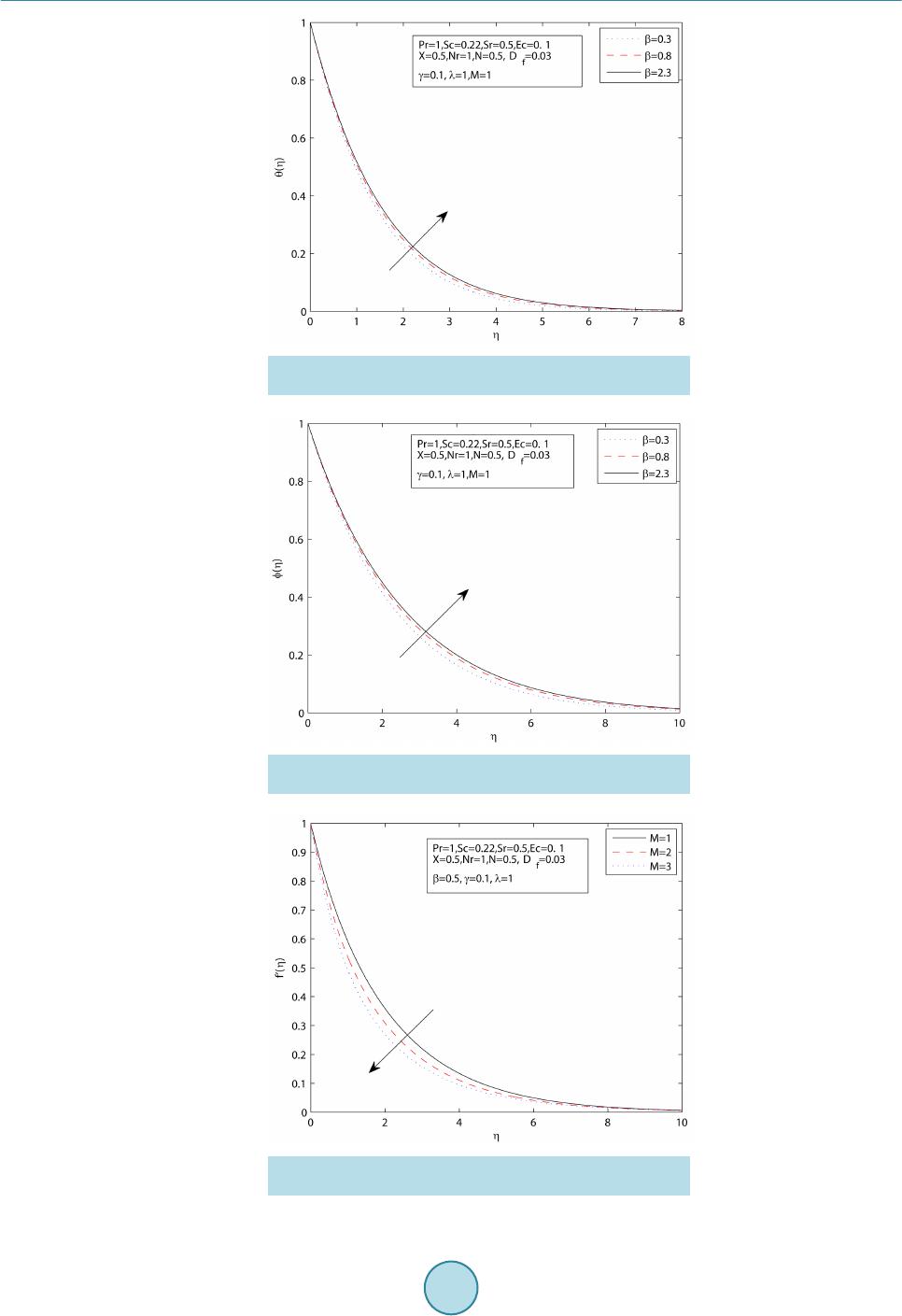

K. Sharada, B. Shankar
172
Figure 6. Temperature profiles for various values of Casson
parameter β.
Figure 7. Concentration profiles for various values of Casson
parameter β.
Figure 8. Velocity profile for various values of magnetic pa-
rameter M.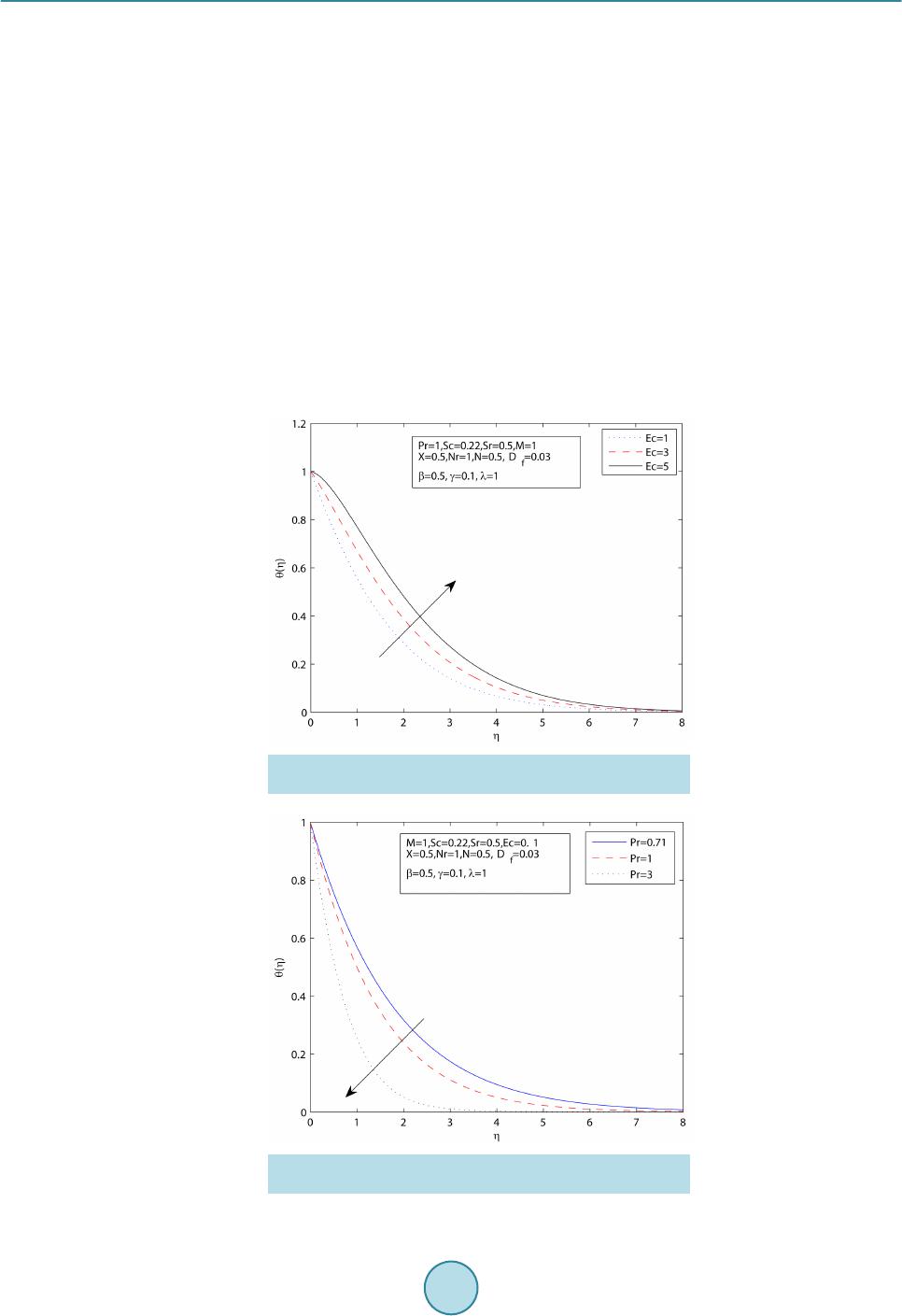

K. Sharada, B. Shankar
173
thickness. Thus the velocity decreases as the magnetic parameter increases.
Increasing the values of the Ec generates heat in the fluid due to frictional heating. Figure 9 demonstrates that
influence of the Ec on the profile of temperature. It is observed that the temperature profile increases as the
value of the Ec increases. The effects of Prandtl number on temperature profiles are shown in Figure 10. Prandtl
number can be used to increase the rate of cooling conducting fluids. Prandtl number signifies the ratio of mo-
mentum diffusivity to thermal diffus ivity. Temperature is found to decrease w ith increasing Pr. Pr = 1, indicates
that the velocity boundary layer and thermal boundary layer are approximately equal.
Figure 11 displays the effect of thermal radiation of the temperature profiles. From this we observe that the
temperature increases with increasing value of the parameter Nr. Figure 12 shows that the effect of Soret on
concentration profile. An increase in the Soret number increases the concentration and the boundary layer
thickness. It is observed that the concentration profile increases as the Sr increases.
Figures 13-15 explain the effects of the X-location on the velocity, temperature and concentration profiles.
From Figure 13, it is observed that the velocity profile decreases with an increase in X in the boundary layer.
Figu re 14 depicts that as the value of X increases, the temperature increases. The concentration profile increases
with as increasing the value of X.
The effect of
f
D
on temperature profile is de picted in Figure 16. The temperature profile increases as
f
D
increases. Figure 17 displays the nature of concentration profiles for various values of chemical reaction
Figure 9. Temperature profile for various values of Eckert
number Ec.
Figure 10. Temperature profile for various values of number
Pr.

K. Sharada, B. Shankar
174
Figure 11. Temperat ure profile for various values of radiation
parameter Nr.
Figure 12. Concentration profile for various values of Soret
number Sr.
Figure 13. Velocity profile for various values of X-location.

K. Sharada, B. Shankar
175
Figure 14. Temperature profile for various values of X-loca-
tion.
Figure 15. Concentration profile for various values of X-lo-
cation.
Figure 16. Temperature profile for various values of Dufour
number Df.

K. Sharada, B. Shankar
176
Figure 17. Concentration profile for various values of chem-
ical reaction parameter γ.
parameter γ. Chemical reaction increases the rate of interfacial mass transfer and reduces the local concentration.
Therefore the concentration profile decreases with an increase of the parameter γ.
6. Conclusions
The numerical solutions for MHD mixed convection flow of a Casson fluid over an exponentially stre tchin g sur-
face with Soret and Dufour, thermal radiation , chemical reaction are analyzed. The results are presented graphi-
cally with various parameters and the values are agreed with previously published work. From the graphical re-
presentations, we have the foll owing obser vations:
• The effect of Casson fluid parameter when treated as fluid with variable plastic dynamic viscosity, the veloc-
ity profile decreases, temperature and concentration distributions are increase d.
• The temperature increases with increasing values of the radiation parameter and Dufour number
f
D
.
• An increase in the mixed convection parameter λ increases the velocity p rofiles, and decreases the tempera-
ture profiles and concent ra tion profi les.
• An increase in the X-location reduces the non-dimensional velocity increase in the temperature and concen-
tration distribution.
• With increasing values of chemical reaction parameter γ, the velocity profile decreases.
An increase in the Soret number increases the concentration profile and the boundary layer thickness.
References
[1] Garnier, M. (1962) Magneto Hydrodynamics in Materials Processing. Philosophical Transactions of the Royal Society
A, 344, 249-263. http://dx.doi.org/10.1098/rsta.1993.0090
[2] Sakiadas, B.C. (1961) Boundary-Layer Behavior on Continuous Solid Surfaces. AIChE Journal, 7, 26-28.
http://dx.doi.org/10.1002/aic.690070108
[3] Crane, L.J. (1970) Flow Past a Stretching Plate. Zeitschrift für Angewandte Mathematik und Physik, 21, 590-595.
http://dx.doi.org/10.1007/BF01587695
[4] Magyari , E. and Keller, B. (1999) Heat and Mass Transfer in the Boundary Layers on an Exponentially Stretching
Continuous Surface. Journal of Physics D, 32, 577-585. http://dx.doi.org/10.1088/0022-3727/32/5/012
[5] Bidin, B. and Nazar, R. (2009) Numerical Solution of the Boundary Layer Flow over an Exponentially Stretching
Sheet with Thermal Radiation. European Journal of Scientific Research, 33, 710-717.
[6] Sajid, M. and Hayat, T. (2008) Influence of Thermal Radiation on the Boundary Layer Flow Due to an Exponentially
Stretching Sheet. International Communications in Heat and Mass Transfer, 35, 347-356.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2007.08.006
[7] Merrill, F.W. (1965) Rheol ogy of Human Blood and Some Speculations on Its Role in Vascular Homeostatics Biome-
chanical Mechanisms in Vascular Homeostatics and Intravascular Thrombosis. In: Sawyer, P.N., Ed., Appleton Cen-

K. Sharada, B. Shankar
177
tury Crofts, New York, 127-137.
[8] MacDonald, D.A. (1979) On Study Flow through Modelled Vascular Stenoses. Journal of Biomechanics, 12, 13-20.
http://dx.doi.org/10.1016/0021-9290(79)90004-6
[9] Nadeem, S., Haq, R.U. an d Lee, C. (2012) MHD Flow of a Casson Fluid over an Exponentially Shrinking Sheet. Scien-
tia Iranica, 19, 1550-1553. http://dx.doi.org/10.1016/j.scient.2012.10.021
[10] Mukhopadhyay, S., De Ranjan, P., Bhattacharyya, K. and Layek, G.C. (2013) Casson Fluid Flow over an Unsteady
Stretching Surface. Ain Shams Engineering Journal, 4, 933-938.
[11] McGregor, J.L. (1970) The Application of the Minimal Energy Hypothesis to a Ca ss on Fluid. Bulletin of Mathematical
Bio Physics , 32, 249-262. http://dx.doi.org/10.1007/BF02476889
[12] Partha, M.K., Murthy, P.V.S.N. and Rajasekhar, G.P. (2005) Effect of Viscous Dissipation on the Mixed Convection
Heat Transfer from an Exponentially Stretching Surface. Heat and Mass Transfer, 41, 360-366.
http://dx.doi.org/10.1007/s00231-004-0552-2
[13] Pal, D. (2010) Mixed Convection Heat Transfer in the Boundary Layers on an Exponentially Stretching Surface with
Magnetic Field. Applied Mathematics and Computation, 217, 2356-2369. http://dx.doi.org/10.1016/j.amc.2010.07.035
[14] Kafoussias, N.G. and Williams, E.M. (1995) Thermal-Diffusion and Diffusion-Thermo Effects on Mixed Free-Forced
Convective and Mass Transfer Boundary Layer Flow with Temperature Depend ent Viscosity. International Journal of
Engineering Science, 33, 1369-1384.
[15] Dursunkaya, Z. and Worek, Z.W. (1992) Diffusion Thermo and Thermal Diffusion Effects in Transient and Steady
Natural Convection from a Vertical Surface. International Journal of Heat and Mass Transfer, 35, 2060-2065.
http://dx.doi.org/10.1016/0017-9310(92)90208-A
[16] Afify, A.A. (2009) Similarity Solution i n MHD Effects of Thermal Diffusion and Diffusion-Thermo on Free Convec-
tive Heat and Mass Transfer over a Stretching Surface Considering Suction or Injection. Communication in Non-Linear
Science and Numerical Simulation, 14, 2202-2214.
[17] Hayat, T., Shehzad, S.A. an d Alsaed, A. (2012) Soret and Dufour Effects on MHD Flow of Casson Fluid. Applied Ma-
thematics and Mechanics, 33, 1301-1312. http://dx.doi.org/10.1007/s10483-012-1623-6
[18] Alam, M.S. and Rahman, M. M. (2006) Dufour and Soret Effects on Mixed Convection Flow Past a Vertical Porous
Flat Plate with Variable Suction. Nonlinear Analysis, Modeling and Control, 11, 3-12.
[19] Pramanik, S. (2014) Casson Fluid Flow and Heat Transfer Past an Exponentially Porous Stretching Surface in the Pre-
sence of Thermal Radiation. Ain Shams Engineering Journal, 5, 205-212.
http://dx.doi.org/10.1016/j.asej.2013.05.003
[20] Shateyi, S. and Marewo, G.T. (2014) Numerical Analysis of MHD Stagnation Point Flow of Casson Fluid, Heat and
Mass Transfer over a Stretching Sheet. Proceedings of the 7th International Conference on Finite Differences, Finite
Elements, Fin ite Volumes, Boundary Elements, Gdansk, 15-17 May 2014, 128-132.
[21] Ishak, A. (2011) MHD Boundary Layer Flow Due to an Exponentially Stretching Sheet with Radiation Effect. Sains
Malaysiana, 40, 391-395.
[22] Mukhopadhyay, S. (2013) Effects of Thermal Radiation on Casson Fluid Flow and Heat Transfer over an Unsteady
Stretching Surface Subjected to Suction/Blowing, Chinese Ph ysics B, 22, Article ID: 114702.
http://dx.doi.org/10.1088/1674-1056/22/11/114702
[23] Shehzad, S.A. and Hayat, T. (2013) E ffects o f Mass Transfer on MHD Flow of Casson Fluid with Chemica l Reaction.
Brazilian Journal of chemical Engineering, 30, 187-195. http://dx.doi.org/10.1590/S0104-66322013000100020
[24] Cebeci, T. and Bradshaw, P. (1984) Physical and Com putational Aspects of Convective Heat Transfer. Springer, Berlin
Heidelberg. http://dx.doi.org/10.1007/978-3-662-02411-9