 Journal of Applied Mathematics and Physics, 2015, 3, 1186-1198 Published Online September 2015 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2015.39146 How to cite this paper: Lacunza, J.C. (2015) The Pendulum of Dynamic Interactions. Journal of Applied Mathematics and Physics, 3, 1186-1198. http://dx.doi.org/10.4236/jamp.2015.39146 The Pendulum of Dynamic Interactions Julio Cano Lacunza Advanced Dynamics CB, Madrid, Spain Email: jcano@coiim.es Received 11 August 2015; accepted 26 September 2015; published 29 September 2015 Copyright © 2015 by author and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract In this paper, we present evidence to show that the dynamics of rigid solid bodies is not a closed discipline, particularly in the field of rotational dynamics. From the observation of bodies with in- trinsic rotation in our universe, our research group proposes new dynamic hypotheses that ex- plain the behaviour observed when these bodies are subject to new simultaneous non-coaxial ro- tations. A new gyroscopic conical pendulum was designed for this purpose. Experimental tests in- itially conducted with this new gyroscopic conical pendulum were repeated for their recording on video, which accompanied this paper for better understanding thereof. These experimental tests positively confirm the new Theory of Dynamic Interactions, and its dynamic laws, which help us to understand the behaviour of this pendulum and, in general, that of the baryonic mass when it is subject to non-coaxial simultaneous rotations. It thus provides a better understanding of the na- ture and the dynamic behaviour of our universe. Keywords Theory of Dynamic Interaction s, Rotating Bodies, Non-Coaxial Spins, Dynamic Interactions 1. Introduction The findings of the Bernoulli’s, Riccati and especially D’Alembert and Euler, followed by that of Lagrange, Laplace and Hamilton, meant that from the 19th century Mechanics could be considered a mathematically de- fined and fully modelled science. However, if we analyze R otational Dynamics specifically, we cannot be satis- fied or share that same approach. It was in fact Euler who established t he equations of motion of rotating solid bodies [1]. His studies on rota- tiona l dyna mic s c ul minate d i n the p ub li ca t io n o f hi s wor k Theoria motus corporum solidorum seu rigidorum [2]. In said work, he expresses the rotation of the main axes of the body in relation to the other three fixed axes, through the use of three variable angles, which determine new angular coordinates, and through very similar formulas to those currently known. 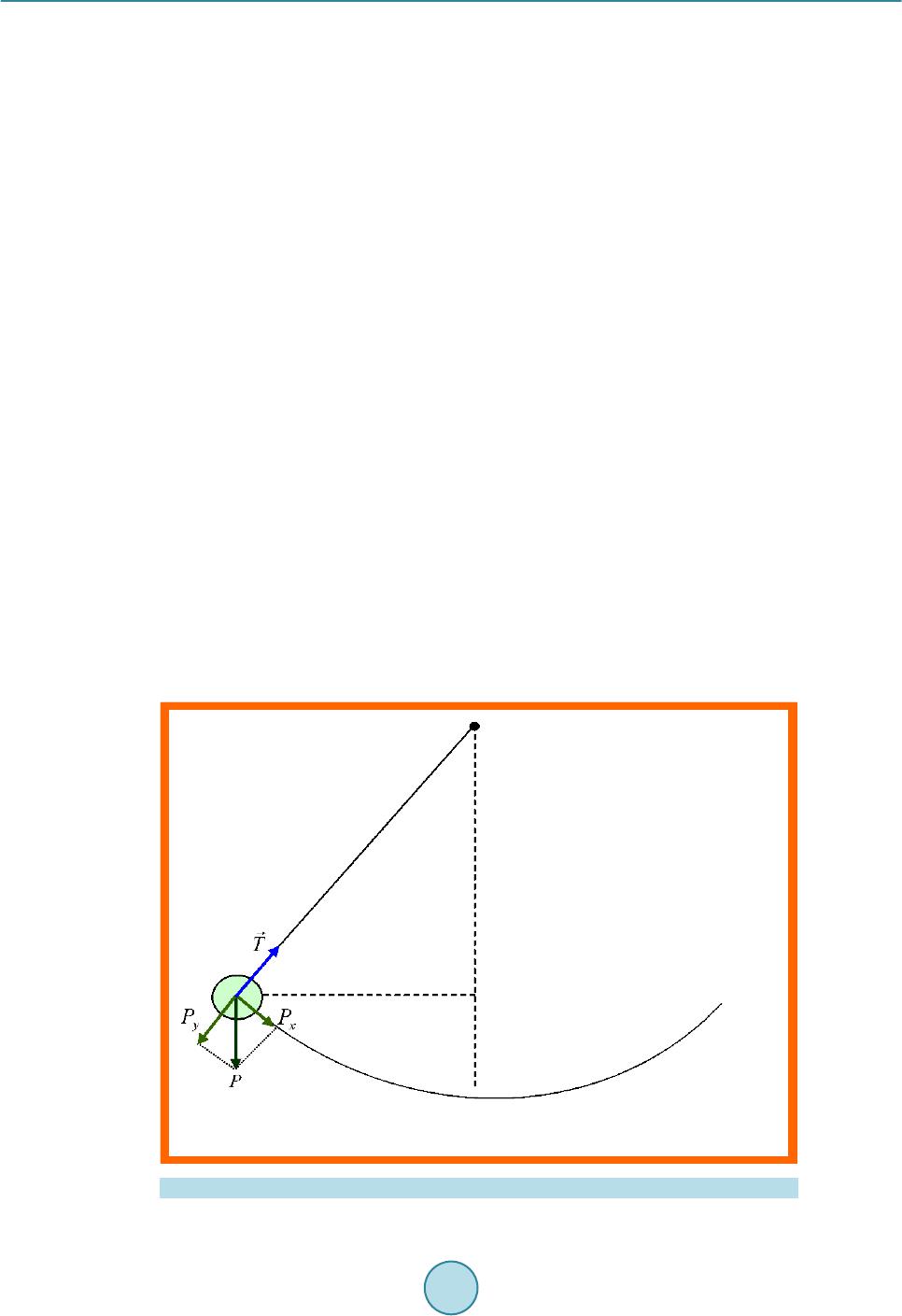 J. C. Lacunza The orientation of a rigid solid body can be determined from Euler’s angular coordinates. If these coordinates are known d epe ndin g on time, we will be able to deduce the te mporal evolution of its o rientation. T hese are Eu- ler’s equations, based on which we should be able to determine the trajectory of a body subjected to multiple momentums. Euler’s equations are to rotational dynamics what Newton’s second law is to translational dynamics. The problem is that those equations, which are consistent and formally correct, do not allow a general solution ap- parently both from the physical and purely mathematical point of view, because they generate complex equa- tions that in most cases can only be solved approximately. I never felt satisfied that some equations of motion would n ot allow a general solution, so, when I discovered a few years ago an alternative proposal based on the Theory of Fields, it appeared to be an attractive solution that caught my i nter e st. 2. The Pendulum By observin g in nature the co nstancy o f the relation ship betwee n orbiting and i ntrinsic ro tation, Gabr iel Barce ló deduced the principle that: Everything that orbits, rotates [3]; or rather, everybody that moves through an orbit simultaneously rotates on an intrinsic axis. He deduced this principle from observing the planetary system, the ring s of Saturn and al so the beha viour of the spi nning t op. He understood, however, the need for empirical checks to confirm or rectify the new dynamic hypotheses de- duced from the aforementioned principle and, where appropriate, to be able to explai n that be haviour b y for mu- lating a new dynamic theory that would simultaneously resolve other Rotational Dynamics phenomena and ge- neralize inertial phenomena. He initially carr ied out various experimental tests, so me of them with pend ulums. A si mple pendulum move s on a p la ne, with t he o nl y fo rc e s e xist i n g b eing the weig ht P and the tens ion of t he st ri ng T, as shown in Figure 1. The pendulum motio n is induce d by the weight of the ha nging mass , whi ch is moved init ially. The laws of the pendulum were amply known and did not require testing. In accordance with Classical Me- chanics, we ass umed t ha t the p e ndul u m wo uld mai nta i n the sa me b e ha vi our i f t he p ass i ve mass of the p e nd ul u m was replace d by a rotor with intrinsic rotation. However, based on his observations and his dynamic hypotheses, Barceló believed that if the neutral mass of the pendulum was replaced by a mass body with intrinsic angular momentum, the behaviour would be clearly different. Figure 1 . Simple pendulum motio n o n a plane [4]. 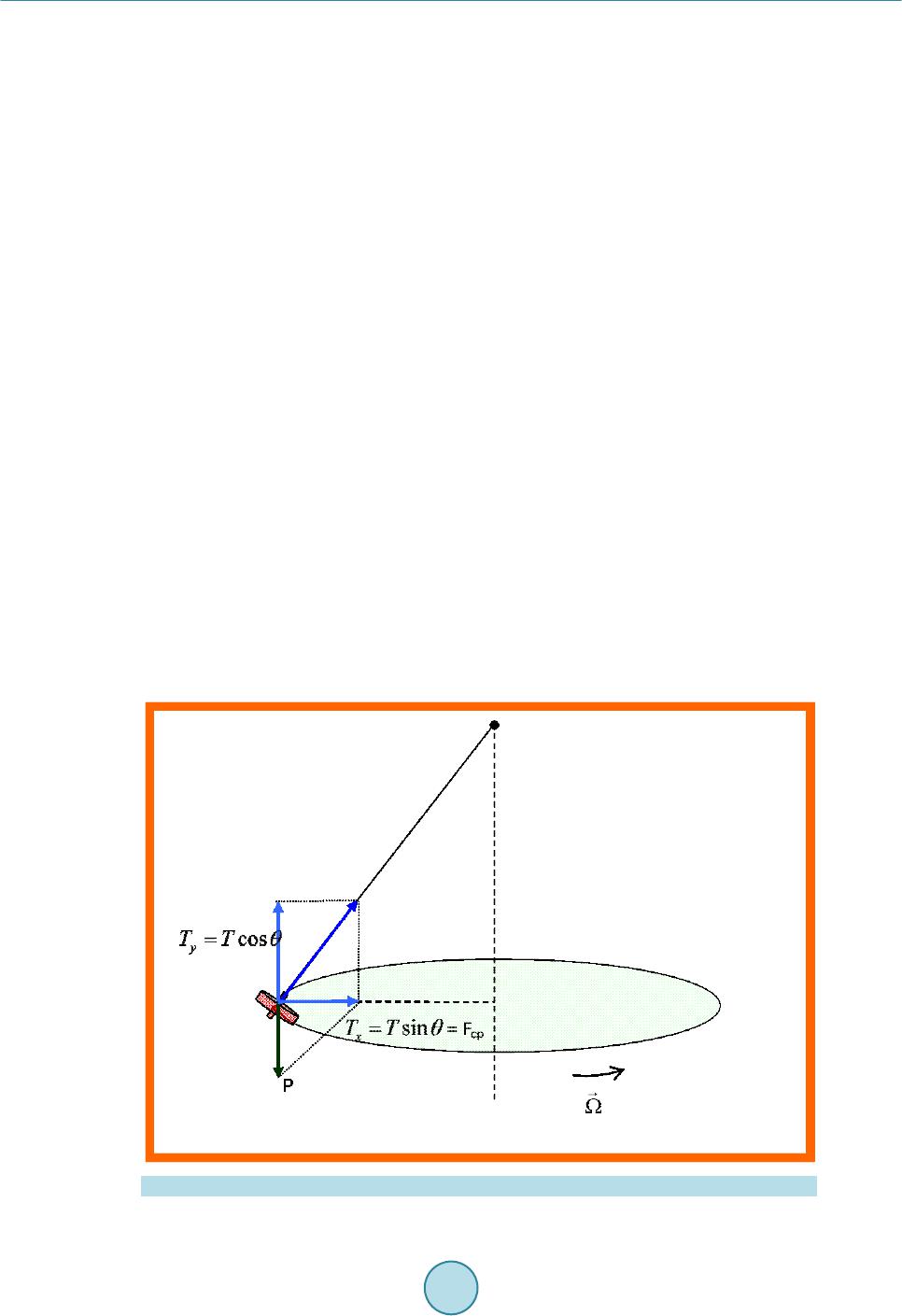 J. C. Lacunza He therefore designed the new pendulum from which he hung a gyroscope (Figure 2). If the pendulum swung without any intrinsic rotation in the gyroscope, it would exhibit the usual behaviour: trajectories only on one plane. However, if the rotor of the gyroscope rotated, he noted that the swinging motion of the pendulum was not limited to a flat trajectory in this case, but it displayed a conical motion in space. It produced an elliptical motion on the horizontal plane. In accordance with Classical Mechanics, the observed spatial movement must have been due to a central force, and would be obtained when the result of the tension of the string T and the weight g m = P were balanced, generating a centripetal force Fcp equivalent to the supposed centrifugal force that determined that trajectory. According to Classical Mechanics, that force was necessary to be able to explain either the circ ular or elliptical movement in space of the pendulum mass. After confir ming that if a gyroscope with intrinsic rotation was suspended, the pendulum would maintain that spatial behaviour, we attempted to determine the reason for this behaviour of the gyroscopic conical pendulum and confirm that this behaviour was not an isolated phenomenon, but rather the usual behaviour of all pendu- lums with masses with intrinsic rotatio n. It should be pointed out that we could observe two non-coaxial ro tations on the new pend ulum: firstly, the in- trinsic rotation of t he ro tor a nd secondl y, the rotatio n of the rotor on the hanging point, due to the pendulum mo- tion. According to Newton-Euler equations, both rotations should generate a new resulting rotation, and the pendulum motion should be maintained on a consta nt plane, as sho wn in traj ectory I of Figure 3. Rather, the pe ndulum ini tiated a spatial movement, si milar to that of traj ectory II of the aforementioned Fig- ure 3. He therefore observed that Classical Mechanics could not account for the behaviour of the pendulu m. It was therefore necessary to also determine the origin of that apparent contradiction and how to correctly formu- late this be haviour, as well as , in case it could b e generalized, the true la ws that de fine the b ehaviour of bod ies subjected to different non-coaxial rotations. From these experimental tests and their findings, Professor Barceló devised and developed the Theory of Dynamic Interactions in order to respond to these rotational phenomena. 3. Analysis of the Experimental Result Firstly, the Advanced Dynamics research group tried to explain this behaviour based on the Classical Mechanics field [6]. Accord ing to the above, in this rational mechanics scenario, the deviation of the pendulum mass could only be possible if there was a centrifugal force equivalent to the centripetal force Fcp that generated that spatial trajec tory, modifying the flat trajec tory which would otherwise maintain an inert mass. Figure 2 . Gyroscopic conical pendulum, with spatial movement [5]. 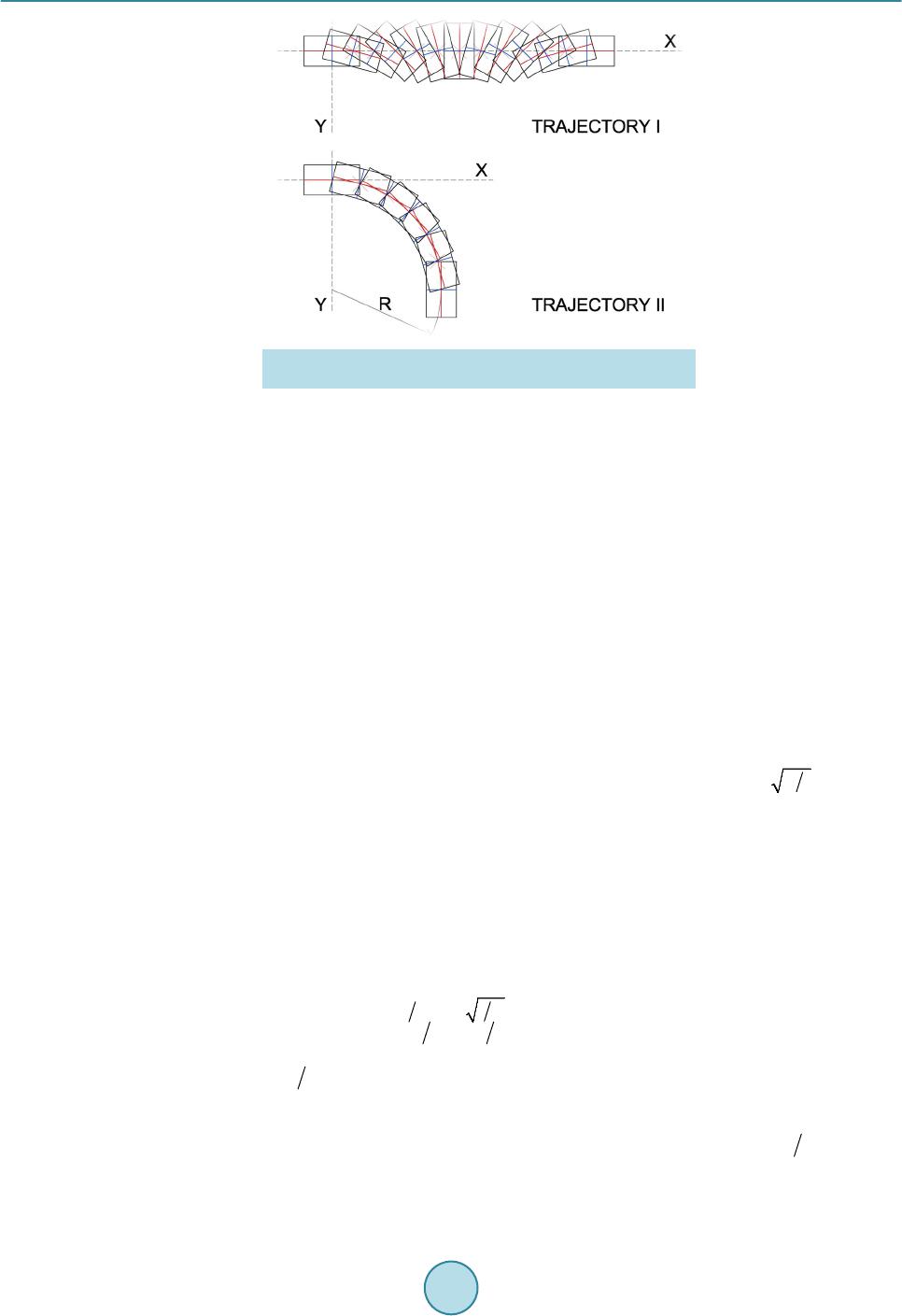 J. C. Lacunza Figure 3 . Classical trajecto ry and trajecto ry predicted with new hypothesis. In accordance with D’Alembert’s principle [7], the centrifugal force indicated in the orbital trajectory of the pendulum mass had to be balanced with the centripetal force Fcp, and, according to Classical Mechanics, would be determined by the equation: F = mV0ω, where V0 is the initial translational velocit y vector , and ω the ang ular velocity of the intrinsic rotation. This apparent force would be perpendicular to the theoretical axis of the pre- cession and the initial linear velocity of the center of gravity of the moving object with intrinsic angular mo- mentum. But such external force did not exist, so we deduced that it was necessary to explore other possible causes within the field of Classical Mechanics, for example, if there might be an aerod ynamic reason, such as air resis- tance, or even the Magnus effect. We could notice some similarity between the phenomenon observed and that of spinni ng balls who s e trajectory i s curved, with the Magnus effect being commonly produced here. Looking at the projection of the movement of this gyroscopic pendulum on a horizontal plane, equivalent to the shadow cast on the ground due to the effect of light from the ceiling on the gyroscope, we noted that it is equivale nt to that o f a point mass on the plane under an attractive force that is always oriented towards the origin. In t his type o f move ment, t he angul ar mo mentum o f the pe ndulu m L re mains unchan ged, where: L = ωmr2 (m, mass of the pendulum; r, distance to or igin of coordinates; ω, angular velocity). For small deviations, the motion of the pendulum can be broken down into two independent oscillations-ac- cording to the X axis and the Y axis-which are 90˚ out of phase, with angular frequency depending on the lengt h of the pe ndulum l ( where g is the gravitational acceleration). Therefore, it follows an ellipse with the center in the coordinate’s origin, which we can place on the vertical line of the equilibrium point of the pen- dulum, specifically on the shadow of this point. For simplicity, we set in motion the pendulum from one of the four vertices of the ellipse at a distance a (s emi-majo r axi s) from t he c e nt er . A fter r el ea si ng the g yr o s co p e o f the p e nd ul u m it mo ve s by gr avi t y, fo llowi ng the trajectory in Figure 2, with a velocity V0. It moves according to the following equations: From the initial cond itions, we have . We noticed how the shadow of the gyroscope pro- duces an ellipse with the following equation : , which could become a circle if a = b. We can analyze the aerodynamic forces involved: • Air resistance ; where cr < 0.5 is the drag coefficient, rB the gyroradius, is the area of the cross-section against the wind, ρA is the air density, v is the velocity, and • The lift force S due to the possible Magnus effect, which could also be determined with an equation equiva- lent to the resistance R, replacing the drag coefficient cr with a lift coefficient cS: . Quantitatively, the supposed apparent precession force F, that could force the pendulum to make its orbit, is far hi gher tha n the for ce S tha t could be generated by the Magnus effect. A careful estimate of the S/F ratio for  J. C. Lacunza pendulum motion on an elliptical path provides a value clearly lower than 0.01, so any possible aerodynamic ef- fect has minimal impact on the actual behaviour of the gyroscopic pendulum. This situation made it p ossibl e to imagi ne that much of t he d ynamic be havio ur attr ibuted to the Magnus effect had not bee n accuratel y asses sed, with that as sumption aris ing from the fact that it wa s difficult to qua ntify and determine, without a true and precise calculation of the phenomenon, and without accurately deducing the true dyna mic behaviour of the bodi es with intrinsic angular momentum. However, doubt remained over whether the actual quantification of the Magnus effect could in fact confirm the results attributed to it, or whether this was a superficial ana lysis of the physic al phenomenon. To reaffirm our result we repeated the experiment with a simple steel ball suspended by a thread and pro- vided with intrinsic angular momentum. We also noticed how the pendulum tended to follow a trajectory not contained on a plane, but with smaller amplitude than before. A ball that moves at velocity V0, rotating on its own axis with an angular velocity Ω, will experience a lift force S perpendicular to the vector V0 and the rota- tion axis of the ball, due to air friction. In the mechanics of tennis and other sports there are approximate em- pirical formulas for that dependence of the velocity ratio v/(rBΩ). However, for the Ω values attained, the force due to the Magn us effect is insufficient to mo ve the steel ball with the resu lt noted, and naturally did not explain the result obtained [8]. The deviation of the gyroscopic pendulum was clear; however, from the tests and calculations the existence of external forces or impact of aerodynamic forces had been ruled out, so the research group felt that there had to be other, hitherto unidentified, dynamic causes. We were faced by the challenge of determining the true nature of that behavioural anomaly of the pendulum with int rinsic a ngular momentum in its mass. In other observations and experimental tests similar phenomena were noticed, such as those in the spinning top, epostracism (throwing stones that bounce on a flat water surface) and the boomerang. In all these other cas- es, if the phenomenon is carefully analyzed, two simultaneous rotations of the body on different axes are also observed, and the coupling of these non-coaxial rotations does not occur. From these observations, the Advanced Dynamics research group deduced that the error was possibly in the application of vector algebra to rotations, so nature did not follow Newton-Euler la ws for non-coaxial simulta- neous rotations acting on the same rigid solid body, free in space. We believed that there was sufficient evidence to assume that it was necessary to devise a new dynamic model to explain that behaviour [9]. Being unable to identify a specific external centrifugal force that would generate the behaviour of the gyros- copic pendulum, and given that said behaviour was only produced when the gyroscope rotated on its main axis, it was obviou s that there was a cause-and-effect correlation. It was therefore deduced that the orbiting movement must have come from the inertial phenome non of dynamic interaction, due to the intrinsic ro tation of the rotor, which had to be discovered and explained. 4. Experimental Tests Professor Barceló made the observations and performed the aforementioned experimental tests, confirming his inertial dynamic hypotheses. Ho wever, no evidence remains from these tests. That is why Alberto Pérez, colla- borator and expert in the theory, wanted to repeat these tests, even designing new specific pendulums with an- gular mome ntum and pro ducing a v ideo with evi dence of the results obtained. This new video can be viewed at the followin g ad dress: www.advanceddynami cs.net/the-pendulum-video. As Alberto Pérez points out in the video, it is important to highlight that the pendulum designed by Professor Gabriel Barceló for his experiments (referred to in his book A Rotating World [10]) had not been previously created. Consequently, the Barceló Pendulum or Pendulum of Dynamic Interactions (PDI) is an invention of this professor, about which we found no historical references or previous information, but which clearly illustrates the tr ue beha viour of natur e, wh en sub mitted to non -collinear multiple rotations. T his pendulum clearl y demon- strates the principles set out by the Theory of Dyna mic Interac tions. As the vide o sho ws, t he Pendulum of Dynamic Interactions is characterized by the fact that, whenever the ro- tor has angular momentum, the pendulum does not swing on a constant plane as pendulums do normally, but ra- ther has spatial oscillation and the gyroscope follows a conical trajectory, moving over the ground in a curved line (Appendix). To e xplain thi s behavi our, Dr. Barce ló propo sed analyzi ng the va riatio n of the di fferent dyna mic ma gnitud es withi n the bo d y itsel f, i n pa rti cula r i n the r ot or c onst itu ting the gravi ta tiona l mass of the p end ulu m, wit h t his a l-  J. C. Lacunza so differentiating it from a classic pendulum. The aim was to apply the Theory of Fields to the body with a dif- ferent trajectory. The video not only shows the existence of a translational velocity field due to the weight, but also other velocity fields gener ated in the rotating mass d ue to its simultaneo us non-coaxi al rotatio ns, requiring furt her ana lysis. Firstly, there was the velocity field generated by the rotation of the disc or rotor about its axis of symmetry, but it was also necessary simultaneously to identify the nature of the velocity field due to a new rotation pro- duced in the rotating disc in its pendulum motion. If the first two fields, translation and rotation, were clearly defined, this third field evolved in a unique way. It was generated as a new non-coaxial rotation, but the main rotation modified its c onfiguration at eac h point of the mass. In t his way we were ab le to identify a new aniso- tropic velocity field, due to the weight torque, but of different magnitude in eac h material po int of the disc, de- pending on i ts position on the new theoretica l axis of rotati on. Each mas s particle cha nges its linear velo city b y the action of that variable momentum, in each of the positions that it traces in a 360˚ rotation. After a rotation, the result will be the generation o f a veloc ity field wit h a new law of distribution. We believe that this description of the dynamic phenomenon analyzed faithfully reflects the true behaviour of nature, and helps to clearly explain the inertia l reactions of the mass of the bo dies and the so-called gyroscopic momentum, too. Having identified the fields that affect the mass, the question now was to define how the magnitudes of those fields could overlap each other or co uple together. We were able to apply the Poinsot hypotheses [11] assumed by Classical Mechanics, and recognize that the fields due to rotations coupled together, outside the translation fields. However, after detailed observation of these phenomena, the Advanced Dynamics research group reached the co ncl usio n that ther e were no gro unds for ma inta inin g t he Po inso t hypo the ses. W e d educ ed t hat the traj ec to- ry observed was explained if we assumed that the velocity field of the rotation of the disc or rotor about its axis of symmetry remained independent and the translational velocity field coupled together with the anisotrop ic ve- locity field generated by the ro ta tion due to the weight torque. The spatial trajectory of the gyroscopic pendulum was therefore duly explained. Furthermore, these same ar- guments could be applied to explain other rotational phenomena observed in the boomerang or the spinning top. A ne w dyna mic mod el co uld b e devi sed in which the o rbit ing move ment was gene rated dire ctly by dynamic in- teraction, i.e. by a coupling bet ween the translational velocity fields of each ma ss p o int of the p endul u m a nd the anisotropic velocity field generated by the new simulta neous non-coaxial rotation. Follo wing these hypotheses, the orbiting trajectory was fully explained and the existence of a supposed fictitious central force was not a pre- requisi t e. We needed t o confi rm w hether the in ertia l behav iour of rot at ing bodi es had more wides pre ad a pplica tion. 5. Theory of Dynamic Interactions If we analyses carefully the result of the experimental tests, [12] we can confirm that the behaviour is similar to other cases observed, such as the submarine, spinning top or boomerang, in which simultaneously non-coaxial rotations are a lso produced. The first experimental tests were carried out by the Advanced Dynamics private research group, and a pres- entation video of these tests was produced [13]. Other tests were subsequently carried out by other independent specialists. For example, Alberto Pérez performed tests with moving objects over land, producing a video [14] and a n a r tic le i n which his ex p er i ment s c o nfi r me d t he new theo ry for e xpl ai ni ng t he mechanic a l be ha vio ur of ri- gid solid macroscopic bodies subjected to rotations, expressing in his conclusions: This article, and the video attached, confirms the above proposal explained by Professor Barceló in his ar- ticle, Analysis of Dynamics Fields in Noninertial Systems, published on Vol. 2, No. 3, June 2012, in the World Journal of Mechanics, even in real inertial conditions. Consequently, I understand that the above theory is a new paradigm of dynamics behaviour. I believe that these conclusions modify the foundations of rational dy- namics and incorporate new criteria of great impact and significance [15]. In all cases, and in accordance with the Theory of Dynamic Interactions, we can say that: The anisotropic distribution of velocities generated by the momentum of the weight, i.e., the velo city field V c, is coupled algebra- ically with the initial translational veloc ity fie ld VT, generating the curved trajectory… [16]. This curved trajectory can be represented by a velocity field VR, obtained by adding the initial translational velocity field VT, wit h the i n ho mo gene ous vel oc it y fiel d Vc, created by the non-coaxial momentu m with the main rotation of the pendulum mass, generating this coupling of fields at each of the mass points of the pendulum ro-  J. C. Lacunza tor. Thi s dyna mic b eha viour has be en exp res sed t hro ugh a si mple equa tion, in wh ic h the resu lt ing sp eed VR is ob- tained fro m the i nitial speed V0, by applying an operator: The operator acts on the initial speed in such a way, that the end speed will be defined by the matrix mul- tiplication of t he operator and the initial speed. This is a general equation of motion for bodies with angular momentum that are subjected to successive non- coaxial torques. For this equation, the rotational op erato r serves as a ma trix tha t tran sfo rms th e initia l velo city, by means of rotation, into the velocity that corresponds to each successive dynamic state [17]. It is possible to establish the design of rotational dynamics based on a physical-mathematical model in line with the obtained experimental results, which is consistent with the sustained dynamic hypotheses and with the expected behaviour in the mathematical model of simulation. We understand that this model, on which the Theory of Dynamic Interactions is based, could be useful for analyzing the dynamic behaviour of bodies in space, with axial symme t ry, in certain specific assumptions [18]. We have understood in the Advanced Dynamics research group that there are numerous examples of this be- haviour, for example the boomerang clearly demonstrates the Theory of Dynamic Interactions. Indeed, the first book published by Professor Barceló about the theory [19], which included a historical analysis of rotational dynamics, bears the very same title. Two articles were subsequently published with a detailed explanation of the dynamic behaviour of the boomerang [20] plus an e xplanatory video [21]. 6. Importance of the Theory Although we have referred in this text to the behaviour of a new concept of pendulum, the impact of this re- search project is difficult to determine. The Theory of Dynamic Interactions not only defines the behaviour of this gyroscopic pendulum but also establishes new conceptual criteria, of a more general nature, to understand the behaviour of nature, meaning that the current laws of dynamics could be considered special and specific cases of this theory. For example, Newton’s laws would apply to the case of a physical model of behaviour, without force mo- ment ums. The Theory of Dynamic Interactions has led to suggestions that the Theo ry of Relativity should be re- vie we d [22] and doubts have been raised over Einstein’s Equivalence Principle [23]. This theory should give rise to a review of the current concepts of astrophysics [24]. There should be special analysis of the subject mat- ter entitled Imago Universi [25] which tells the fascinating history of human knowledge of the universe, while also proposing, developing and explaining the application of the Theory of Dynamic Interactions to afford us a better understa nding of the d ynamic enigmas t hat surround us. A webpage has been published [26] and a pres- entation video produced [27] on t his te xt. This theory has also had numerous technological applications [28], with its application being devised in the control of moving objects, in astronautics [29], in nuclear fusion plants [30] or for interpreting climate pheno- mena with rotating fluid masses, such as typhoons or tornadoes [31]. 7. Conclusions We have presented evidence to show that the dynamics of rigid solid bodies is not a closed discipline and that new ho rizons for d evelopi ng this sub ject matter can be o pened up, particularly in the field of rotational dynam- ics. We have proposed confirmation of the principle that in nature “Everything that orbits, rotates”, by observ- ing the behaviour of a new gyroscopic pendulum. The tests carried out and behaviour observed in this new pendulum have been described and repeated. The statement of the new Theory of Dynamic Interactions has been recorded and repeated, and is more generalist, struc tured , with d efined laws [32] for bodies submitted to non-coaxial si multaneous rotatio ns, helping us to bet- ter understand the nature and dyna mi c behavio ur of o ur un iver s e. In light of the above, we can sa y that t he initial dynamic hypotheses have been confirmed and verified from the exp e ri me nta l tests c o nduct ed , co nfirming t ha t the b eha viour o f this gyr o sc op ic p end ulu m a nd , ge ner all y, tha t of bodies with intrinsic rotation submitted to non-coaxial simultaneous rotations is consistent with the predic-  J. C. Lacunza tions of the Theory of Dynamic Interactions. All of this can be checked by watching the video with the experi- mental tests performed at the following address: www.advanceddynamics.net/the-pendulum-video. References [1] Euler, L. (1750) Die Entdeckungeines neuen Prinzips der Mechanik. History of the Royal Academy of Berlin, 185-217. [2] Euler, L. (1790) Theoria motus corporum solidorum seu rigidorum. Rostock. Other Edit., Greifswald, 179 0, 30 1. [3] Barcel ó, G. (2005) The Flight of the Boomerang (El vuelo del bumerán). Ed. Marcombo, Barcelona, 43. http://www.dinamicafundacion.com/ [4] Barcel ó, G. (2008) A Rotating World (Un mundo en rotación). Ed. Marcombo, Barcelona, Figure 5.1. http://www.dinamicafundacion.com/ [5] Barcel ó, G. (2008) A Rotating World (Un mundo en rotación). Ed. Marcombo, Barcelona, Figure 5.2. http://www.dinamicafundacion.com/ [6] Barcel ó, G. (2008) A Rotating World (Un mundo en rotación). Ed. Marcombo, Barcelona, Chap. 4. http://www.dinamicafundacion.com/ [7] D’Alembert (1749) Recherches sur la précession des équinoxes et s ur la nutation de l’axe de la terre. P ar is, 1749. [8] Barcel ó, G. (2008) A Rotating World (Un mundo en rotación). Ed. Marcombo, Barcelona, 108. http://www.dinamicafundacion.com/ [9] Barcel ó, G. (2005) The Flight of the Boomerang (El vuelo del bumerán). Ed. Marcombo, Barcelona, 121. http://www.dinamicafundacion.com/ [10] Barceló, G. (2008) A Rotating World (Un mundo en rotación). Ed. Marcombo, Barcelona. http://advanceddynamics.net/en/un-mundo-en-rotacion/ http://www.dinamicafundacion.com/ [11] Poinsot, L. (1834) Théorie nouvelle de la rotation des corps. [12] Theory of Dynamic Interactions. Videos. http://www.youtube.com/watch?v=P9hGgoL5ZGk&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=XzTrGEtJGXU&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=dtMqGSU9gV4&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=qK5mW2j2nzU&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=vSUkd4slHGQ http://www.youtube.com/watch?v=P9hGgoL5ZGk&feature=c4-overview-vl&list=PL3E50CF6AEBEED47B [13] Bauluz, E. New Dynamic Hypotheses. This Video Showed the Experiments Carried out by Advanced Dynamics to Prove and Explain the Theory of Dynamic Interactions. www.advanceddynamics.net http://vimeo.com/62601974 http://dl.dropbox.com/u/48524938/VTS_Ingles.mov http://www.youtube.com/watch?v=vSUkd4slHGQ&feature=c4-overview&list=UUgDHgaGi2I2rmZNo anNbVWQ [14] Pérez, L. A. (2013) Reflecting Ne w Evidence on Rotational Dynamics. Video. http://vimeo.com/68763196 [15] Pérez, L. A. (2013) New Evidence on Rotational Dynamics. World Journal of Mechanics, 3, 174-177. http://www.scirp.org/journal/wjm http://dx.doi.org/10.4236/wjm.2013.33016 [16] Barceló, G. (2015) Theory of Dynamic Interactions: The Flight of the Boomerang II. Journal of Applied Mathematics and Physics, 3, 545-555. http://www.scirp.org/journal/jamp [17] Barceló, G. (2012) Analysis of Dynamic Fields in Non-Inertial S yst ems . World Journal of Mechanics, 2, 175-180. http://dx.doi.org/10.4236/wjm.2012.23021 [18] Álvarez, A., et al. (2007) Mathematical Model on Rotational Dynamics. First International Congress on Maths, I. and A. UP Madri d, ETSICCP. [19] Barceló, G. (2005) The Flight of the Boomerang (El vuelo del bumerán.) Ed. Marcombo, Barcelona. P art II: Chap. 4 to 7. http://www.dinamicafundacion.com/ [20] Barceló, G. (2014) Theory of Dynamic Interactions: The Flight of the Boomerang. Journal of Applied Mathematics and Physics, 2, 569-580. http://dx.doi.org/10.4236/jamp.2014.27063 http://www.scirp.org/journal/jamp [21] Sanchez Boyer, J. (2015) The Flight of the Boomerang II. Video. https://www.dropbox.com/s/stng5b2co1441hk/Boomerang_ENG_mini.mp4?dl=0 https://www.youtube.com/watch?v=mGfrGW5fhOg&feature=youtu.be  J. C. Lacunza https://vimeo.com/129383447 [22] Barceló, G. (2014) On Motion, Its Relativity and the Equivalence Principle. Journal of Modern Physics, 5, 1839-1847. http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=51422#.VHB0jzSG_To http://dx.doi.org/10.4236/jmp.2014.517180 [23] Barceló, G. On the Equivalence Principle, AC-10-A.2.1.1. 61st International Astronautical Congress, Prague, CZ. [24] Copyright © 2010 by Advanced Dynamics. Published by the American Institute of Aeronautics and Astronautics, Inc. http://www.coiim.es/forocientifico/FORO%20CIENTFICO/Documentos/ON_THE_EQUIVALENCE_P R I NC IPLE.pd f [25] Barceló, G. (2013) Proposal of New Criteria for Celestial Mechanics. International Journal of Astronomy and Astro- physics, 3, 385 -391. http://dx.doi/org/10.4236/ijaa.2013.34044 [26] Barceló, G. (2013) Imago Universi: A Story of the Human Conception of the Cosmos. Ed. Arpegio, Barcelona. http://www.editorialarpegio.com/ http://imagouniversi.com/ [27] Sanchez Boyer, J. Imago Universi. Video. https://vimeo.com/62247544 [28] Barceló, G. (2013) Technological Applications of the New Theory of Dynamic Interactions. Global Journal of Re- searches in Engineering: Mechanical and Mechanics Engineering-G, 13. https://globaljournals.org/GJRE_Volume13/E-Journal_GJRE_(G)_Vol_13_Issue_5.pdf [29] Almudena, M . G. (2015) Simulador de vuelo, viaje a Saturno. E.T.S.I. Aeronáuticos (U.P. Madrid). Final Coursework Project. [30] Barceló, G. (2014) Dynamic Interaction Confinement. World Journal of Nuclear Science and Technology, 4, 249-260. http://www.scirp.org/journal/PaperInformation.aspx?paperID=51026& http://dx.doi.org/10.4236/wjnst.2014.44031 [31] Barceló, G. (2014) Dynamic Interactions in the Atmosphere. Atmospheric and Climate Sciences. 4, 828-840.http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=51584#.VHB4YTSG_To [32] Barceló, G. (2013) Theory of Dynamic Interactions: Laws of Motion. World Journal of Mechanics, 3, 328-338. http://dx.doi.org/10.4236/wjm.2013.39036 [33] Barceló, G. (2008) A Rotating World. Ed. Mar combo, Barcelona, 104. http://advanceddynamics.net/en/un-mundo-en-rotacion/ http://www.dinamicafundacion.com/ [34] Barceló, G. (2008) A Rotating World. Ed. Mar combo, Barcelona, 105. http://advanceddynamics.net/en/un-mundo-en-rotacion/ http://www.dinamicafundacion.com/ [35] Barceló, G. (2008) A Rotating World. Ed. Marcombo , Barcelona, 106. http://advanceddynamics.net/en/un-mundo-en-rotacion/ http://www.dinamicafundacion.com/ [36] Barceló, G. (2008) A Rotating World. Ed. Mar combo, Barcelona, 108. http://advanceddynamics.net/en/un-mundo-en-rotacion/ http://www.dinamicafundacion.com/  J. C. Lacunza Appendix Video Script The Pendulum of Dynamic Interactions A pendulum is a physical system with a mass hanging from a fixed point by a string or a rod, and which can swing freely due to gravitational action. Any other interaction, such as a magnetic field or material elasticity, can also cause a pendulum to oscillate. The p end ulu m has be e n used in va r io us wa ys si nc e a ntiq u it y: ti me meas ur e ment , me tr ono me , meas ur e me nt of gravitational field strength, etc. Undoubtedly the most popular application of the pendulum is time measurement. This application has its origins in the observations made by Galileo. Around 1581, when in the Cathedral of Pisa, Galileo observed the movement of a hanging lamp. He looked at it and no tice d so me thi ng tha t ca use d hi m to repeat various experiments with pendulums, allowing him to confirm a phenomenon which showed that al- though the amplit ude of the oscillatio ns was reduced, the os cillation frequency d id not depend on the a mplitude or t he suspende d weight, but only on the distance to t he fixing p oint. This phenomenon was called isochronism, and helped to give this researcher the intuition of to develop his Law of falling bodies. Later, Christian Huygens in 1656 repeated these studies, and discovered that the period during which each length of suspended chord oscillated was constant. He concluded that, since small oscillations of the pendulum are isochronous, it was useful for measuring time. This led him to develop the pendulum clock, the most precise for calculating time until the 1930s. Depending on their configuration and use, there are many different types of pendulums. They usually bear the names of their creators or their main feature: simple pendulum, cycloidal pendulum, double pendulu m, Fouc a ult pendulum, Newton’s cradle, torsion pendulum, etc. Ne wto n ’s cradle is a device that displays the conservation of linear momentum. It consists of a set of identical pendulums with solid balls as a suspended body, positioned so that the balls are perfectly and precisely horizontally aligned and just in contact with their adjacent balls when motionless. Each ball is suspe nded fro m a pair of wires o f equal le ngth so a s to restr ict the move me nt o f the balls in the sa me ver- tical plane. Dropping a ball from one of the ends knocks the rest tra nsferring the amo unt of movement t o the ball at the other end which will shoot up, theoretically to the same height as the initial ball, before falling subse- quentl y b y gra vit y and r epe ating t he p heno meno n fro m the opposite direction. This is how pendulum movement is started. A Foucault pendulum, named after its inventor, Leon Foucault, was used to demonstrate the Earth’s rotation and the Coriolis effect, described in 1836 by the French scientist Gustave-Gaspard Coriolis. This audiovisual document provides an outline of the behaviour (from a mechanical and dynamic point of view) of a new pendulum. This is a device developed following the principles contained in the Theory of Dy- namic Interactions, set out by Professor Gabriel Barceló in his publication A Rotating World in 2008. We have not found any previous historical references for this pendulum. Hereafter we refer to this pendulum as the Pendulum of Dynamic Interactions (PDI). Thanks to it we will car ry out a n e xp e r iment to de monstrate the principles set out b y the Theory of Dyna mic I nteractions (Figure 4). Let us briefly de scr ibe it: Like any pendulum, it has a suspension string. The body or suspension system is a gyroscope, i.e., a device consisting of 2 very d ifferent parts fro m a mechanical and dyna mi c po i nt of vi ew: 1) T he “stator”; it is a rod, which serves as the axis and is attached by one end to the pendulum suspension wire. The rod must be able to pivot freely on the union. 2) The “rotor”; it is a ri gid b od y, ideall y ro tating, whic h rot ate s on the “stator” axi s. The c ent er o f ma ss o f t he rotor must no t be o n the strai g ht line of the su spen sion string. Gr avitatio nal i nteractio n t he refore pro vides to rque to the rotor, without the location of the point the rotor center will pivot on having any significant relevance. Theor etically and ideall y, this rotation is co mpletely inertial, i.e., without ac celerations t hat force the ro tor to in- crease or decrease its angular velocity. The Pendulum of Dynamic Interactions is characterized by the fact that, if the rotor has an angul ar mo me nt u m, the plane o f the p end ul um swing is not c onstant, unli ke other pendulums. In the aforementioned text, A Rotating World, Gabriel Barceló recalls his initial tests with a pendulum: In  J. C. Lacunza Figure 4. Pendulum of dynamic interactions: secondary torque, which is driven by gravity and rectilinear Momentum. 1992 I began conducting experimental tests with simple pendulums supporting a gyroscope. If we maintain the gyroscope with its own rotation, suspended from its axis by one of its ends, it will begin an orb iting movement. Besides the precession of the gyroscope, an unintended action is evident, since the pendulum no longer main- tained the same oscillation plane, following a trajectory whose projection on the ground is a curved line. This reaction disappears if the gyroscope stops rotating, producing in this case the usual flat swing of the pendulum [33]. He did confirm repeatedly that this pendulum which he had designed with a rotating gyroscope did not swing in a plane, and that the gyroscope modified its spatial position as soon as it started its intrinsic rotation. He add- ed: In a gyroscopic conical pendulum, movement is not limited to a plane, as the gyroscope that constitutes the weight follows a trajectory in space, even without momentum… …it was also obvious that this was not the Foucault Pendulum case, and therefore a change in the trajectory was not due to the movement of Earth’s rotation or any other external agent: there was a clear cause and effect between the rotation gyroscope and its trajectory. This could be proof positive that orbiting and rotation were not independent, so they should not be treated as such ; we analyzed with interest the behaviour of this pendulum [34]. Initially Barceló thought about the possible existence of a central force that generated the trace in space, and not constantly in a ve rtical plane, and even i f i t was d ue to an externa l age nt , so he express ed in his boo k: However, we had to determine its true cause, for example if air resistance, the Magnus effect, or another aerodynamic effect generated this force. For our purposes, it was sufficient to consider the projection of the pendulum motion of the gyroscope on a horizontal plane, i.e., the shadow cast on the ground due to the effect of light from the ceiling on the gyroscope. Let us fix, within this plan e, the origin of our coordinate system on the point of equilibrium of the pendulum, more precisely, on the shadow of this point. The movement of the shadow of the pendulum is the same as that of a point mass on the plane under an attractive force [35]. After repeating the experiment with a simple steel ball suspended by a rope and provided with intrinsic angu- lar momentum, he came to the conclusion that …the force due to the Magnus effect is insufficient to move the steel ball with th e anticipate d result, and obviously it did not justify the obtained result. Having discounted the Magnus effect, or any other exter nal agent, he t hought that there was not any kind of outside force that could generate the obtained trajectory in this pendulum but, with its deviation still evident, Barceló concluded that there had to be other hitherto unidentified cau ses: However, there was also enough evidence to suppose that the precession was only generated by an inertial phenomenon of dynamic interaction, without the existence of a central force being a prerequisite. It was then necessary to devise a new dynamic model to justify this behaviour. The actual existence of that inertial force had to be ide ntifiable and measurable by the effect caused by the supporting rope… …It could be conceived a new dynamic model, in which…the orbiting movement is generated directly by dy- namic in teraction, i. e., by a coupling between the linear speed of the trajectory of the center of mass of the pen- dulum a nd its intrinsic rotation (Figure 5). The existence of a central force was not a prerequisite in this hypo- 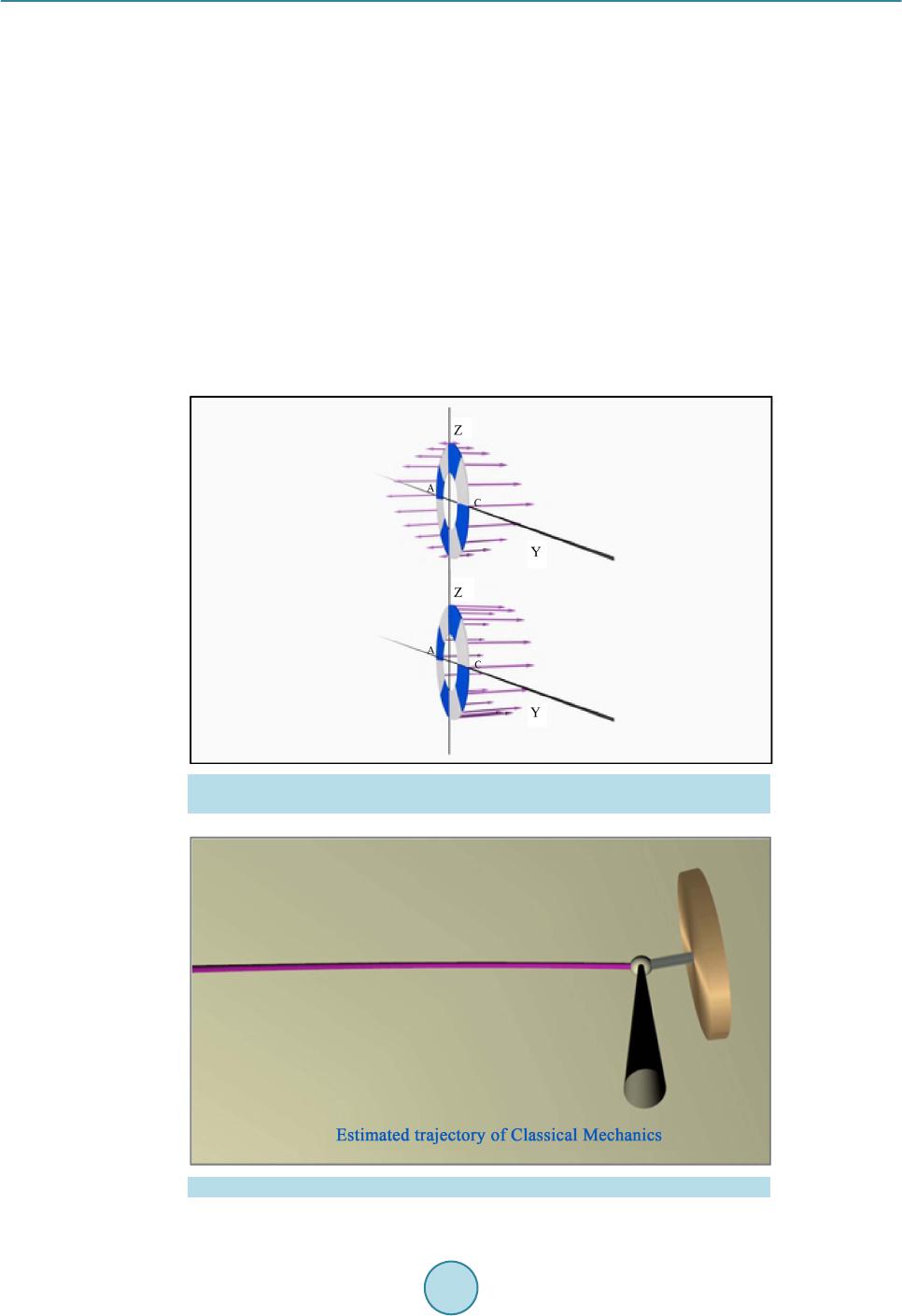 J. C. Lacunza thesis, despite the apparent motion induced by a force of this kind. It was necessary to confirm whether it was possible to generalize the inertial behaviour of rotating bodies [36]. This intuition, watching that pendulum suspended with a gyroscope in rotation, allowed him to develop the Theory of Dynamic Interactions. This us es the T heor y of Fi elds to expla in this p henome non, a nd inter pret other multiple phe nomena of rotational dynamics. In the system studied we have all the necessary ingredients required by the Theory of Dynamic Interactions: - A Main Angul ar Momentum on the rotor part of the hanging bod y. - A Secondary Torq ue, which is driven by gravity. - A Rectilinear Momentum, inherent charac t eristic of any hanging body in any f unctional p endulum. Therefore, Barceló could watch how the oscillating mass exhibited a variation in its initial Rectilinear Mo- mentum in ter ms of direction. This is due to the fact, acco rding to the Theory of Dynamic Interactions, that the field of anisotropic velocities, generated by the so-called Secondary Torque (the weight of the rotor in the gy- roscope) is dynamically coupled with the Translational Velocity Field, with the initial Main Angular Momentum remain ing constant. We not observed the estimated trajectory of Classical Mechanics (Figure 6). The observed curved path corresponds to algebraic sums of Velocity Fields, whereby we observe a swinging pendulum in space but not in a constant plane (Figure 7). Figure 5 . The field of anisotropic velocities, generated by the secondary torque is dy- namically coupled with the translational velocity field. Figure 6 . Estimated trajectory of Classical Mechanics.  J. C. Lacunza Figure 7 . Real trajectory of the pendulum of dynamic interactions. Due to the natural effect of Dynamic Interactions described by the Theory of Dynamic Interactions, we are looking at a behaviour that bears no resemblance to any other pendulum in history: The Pendulum of Dynamic Interactions, discovered by Barceló, shows a peculiar behaviour, its center of mass marking a special trace that can be justified by referring to the Theo ry of Dynamic Interactions. This theor y holds that a d yna mic coupli ng bet ween t he tran slational velocit y field and the anisotro pic velo cit y generated by the non-coaxial force will occur. This field overlapping will produce a new curve trajecto ry o f t h e center of mass of the body, equivalent to that exerted by a central force without the existence of it. Thr ough his s tudies a nd tria ls, Ba rceló ha s come to r ealize that the observe d beha viour in t his pe ndulum c an be generalized to all free bodies in space that have intrinsic angular momentum and rectilinear translational mo- tion ( linear moment um) whe n the y are subj ecte d to new tor ques or new non-coaxial forces with the existing an- gular mo me nt um. T hi s b eha vi o ur e ven r e pr e sent s evi dence of a p o ssib le transfer of rotational dynamic energy to translational dynamic energy or vice versa. In the event t hat the a cti ng torq ue is con sta nt, as in t he ca se of gra vity, the de viation will also be co nstant, o b- taining as a trajectory a closed orbit that turns into a spiral caused by friction with the earth’s atmosphere. This was how Barceló also became convinced that, in nature, bodies that orbit also rotate, with a mechanical correlation existi ng be tween both natural p henomena.
|