Abstract

The paper examines a motive for R&D cooperation with a rival by considering the behavior of a quality follower in a model of vertically differentiated products. We show that, in some settings, a quality follower has an incentive to contribute money to R&D activity of a quality leader with the sole purpose of making the leader’s products even better. The reason behind this motivation is that the leader’s product quality is serving as an upper-constraint in the decision process of the follower regarding product quality selection. Thus, if the leader’s product quality is raised both firms will be better off.

1. Introduction

A firm’s motivation for R&D cooperation is commonly associated with that firm’s ability to acquire knowledge - its endogenous absorptive capacity (see [1,2]). Cassiman and Veugelers [3] refined the concept of absorptive capacity into incoming spillovers and outgoing spillovers. The concepts of incoming and outgoing spillovers relate to the “amount” that external knowledge becomes an “asset” to a firm, and the amount that a firm’s knowledge that can be utilized by other firms respectively. Thus, incoming spillovers will motivate a firm to seek R&D cooperation but outgoing spillovers will exert the opposite effect. Firms tend to limit outgoing spillovers through secrecy measures, greater complexity of developed knowledge, or through the application of proprietary rights to prevent competitors from using this knowledge. Besides, some studies focused on R&D cooperation between producers of complementary products [4] while other authors emphasized the role of uncertainty and cost sharing for the generation of new knowledge [5]¹.

However, many previous works on quality choices have suggested that the quality follower should intentionally limit its product quality so as to relax direct competition from the quality leader, even though it might increase the quality level without any cost [7-9]. Other papers which considered quality cost also came to a similar conclusion that the quality follower selects a low quality level to avoid intensive price competition [10,11].

For this reason, the leader’s product quality serves as an upper constraint in quality choice process of the follower. Put differently, if the leader does not increase its product quality, the follower may have no incentive to increase its product quality. Intuitively, the follower may relax price competition by helping increase the leader’s product quality instead of limiting product quality of its own. But if this constraint is relaxed, what will be the effect on the potential for cooperation?

In this paper, we identify another motive for R&D cooperation that is purely related to the chosen ‘locations’ of a leader and a follower on a scale of product quality. We suggest a follower can stimulate a leader to increase its product quality by contributing an amount of money to the leader, i.e. just enough to cover the margin between R&D cost and expected additional profit. In taking this action, the follower can select a higher product quality level without worrying about the severe competition in the price selection stage. This motive is not related to new knowledge acquired by the follower from R&D, as the follower can move to its new location with only its current knowledge. Both parties having some motivation for cooperation, we now proceed our model, followed by a discussion of empirical considerations regarding its applicability.

2. The Model

An industry with a product that can be vertically differentiated is considered. There are two firms that produce functionally identical products, but of different quality. The products are sold to a population of consumers with different quality willingness to pay. Each consumer may purchase a product from one of the firms or may not buy any product at all.

The consumer’s preferences are described as follows:²

(1)

Here q is the unit of quality built in the product, and p is its price. Note that this function is an indirect utility function of consumer i, with quality preference identified by the parameter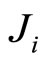. The total number of consumers is normalized to 1. When described by the parameter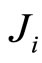, we assume they are distributed uniformly between 0 and b. Consumers will decide to purchase the product that gives a higher and non-negative utility.

We assume there are two firms, ‘firm 1’ and ‘firm 2’. Similar to the assumptions of Wauthy [7], we assume that firm 2 can build any level of quality into its products such that 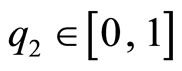with zero quality cost³. Similarly, firm 1 can choose any (d >0). We can regard the each firm’s capability to select quality level as the firm’s current internal knowledge that is as a result of past R&D activity. Note that this R&D cost has been sunk or it does not affect our model’s findings. Production cost is zero for both firms.⁴

Suppose there is an opportunity for both firms to assuredly increase their internal knowledge by investing in R&D activity. If firm 1 invests a fixed cost of F in R&D activity, the new knowledge will increase the firm’s range of quality choice by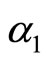. By making a fixed investment of F in its R&D activity, firm 1 can choose any level of product quality such that. Similarly, firm 2 can select any quality level of its product such that if it invests in R&D activity with a fixed cost of F.

Further assumptions: 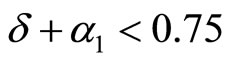and.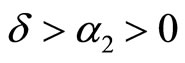

We will see that with this first assumption, the optimal quality level for firm 2 will lie in the interval of [0,1] or firm 2 does not need any new knowledge to move to any new location here. The second assumption eliminates the circumstance that both firms engage in a R&D race (firm 2 may become a quality leader).

We model a game consisting of three stages. In the first stage, both firms decide to invest or not invest in R&D activity on their own. If they don’t invest in R&D activity of their own, they can decide to contribute an amount of money to support the other firm’s R&D activity. In this case, however, it cannot get any new knowledge in return. In the second stage, both firms select the quality levels of their products. In the final stage, firms simultaneously compete in price.

Because at the outset we do not know which of firm 1 or firm 2 will introduce products with higher quality we will call the firm offering the high quality product, the high quality firm and  the product quality level of this firm will be. Similarly, we denote the firm producing the low quality product the low quality firm and its quality level will be.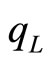

The marginal consumer who is indifferent between buying high quality and low quality products is defined by

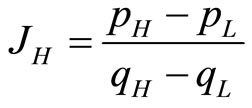(2)

In Formula (2), 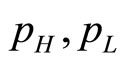and 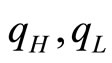are prices and quality levels of high quality products and low quality products, respectively. The marginal consumer who is indifferent between buying and not buying a low quality product is:

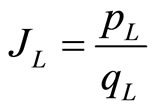(3)

Because each consumer can buy at most one product, the demand for a high-quality product is the number of all consumers above the marginal consumer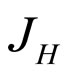 (who is indifferent between a high-quality product and a lowquality product). The demand for a low-quality product is all consumers above the one who is indifferent between buying a low-quality product and not buying.

2.1. Third Stage: Bertrand in Price

From (2) and (3), we can derive the quantity demanded for low-quality and high-quality products as follows:

(4)

(5)

If firms invest in R&D activity, this R&D investment is considered to be a fixed cost and treated as a sunk cost in the third stage. Thus, we do not need to put this cost into our consideration in this stage. The corresponding profit functions (without considering the cost for R&D investment) are as follows:

(6)

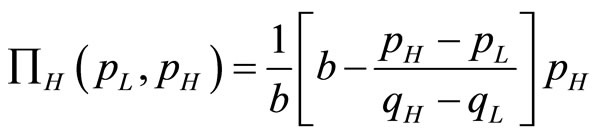(7)

The best response of the low quality firm to price, , is derived from the first order condition (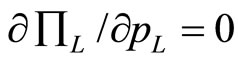), which is

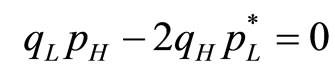(8)

Similarly, the best response of the high-quality firm on price, 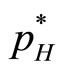, is derived from the first order condition (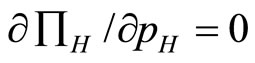), which is

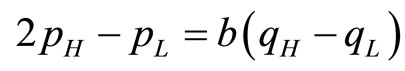(9)

The Nash Equilibrium is derived by solving (8) and (9) with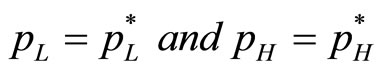. We have the optimal prices as follows:

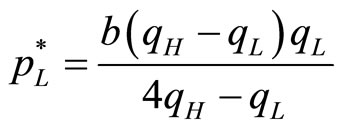(10)

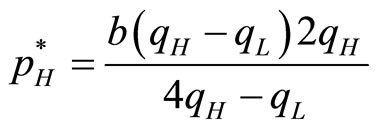(11)

Substituting (10) and (11) into (6) and (7), we find profit functions of the high quality and low quality firms to be:

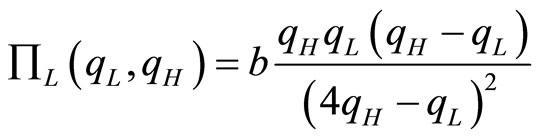(12)

(13)

2.2. Second Stage: Quality Choices

Differentiating Equation (13) with respect to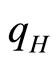, we have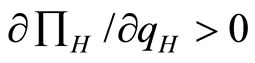. Thus, the profit function of the high quality firm increases as increases. Therefore, the high-quality firm will choose the highest level of quality. That is,

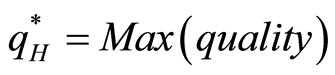(14)

The optimal quality level of the low-quality firm, 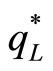, is derived from the first order condition. Differentiating Equation (12) with respect to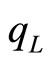, setting it to zero, and using Equation (14); we arrive at

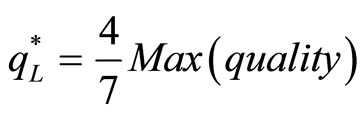(15)

Proposition 1: Regardless of what effort firm 2 makes in the first period, firm 1 will produce high quality products while firm 2 will produce low quality products.

Proof: By comparing (12) with (13), we get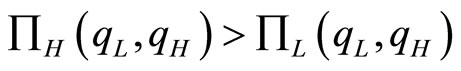. Thus, both firms want to be the high-quality firm because they can get higher profit. With the assumption that 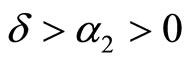(or 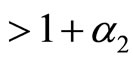), even if firm 2 invests in R&D activity, the highest quality level of its product is only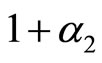, while firm 1 can produce at least a product with a quality level of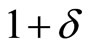. For this reason, firm 1 is the high quality firm and firm 2 is the low quality firm.

Proposition 1 implies that firm 2 cannot surpass firm 1 in terms of product quality. It must accept a position of the quality follower. Firm 1 is the quality leader in the market.

1)    If firm 1 invests in R&D:

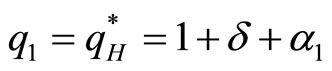(16)

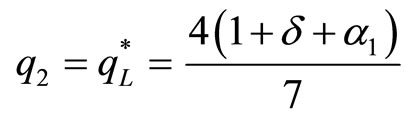(17)

It is worth noting that 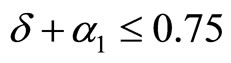implies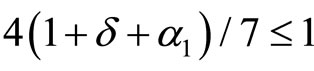. Thus, firm 2 can produce products as in (17) because it already has enough knowledge (it can select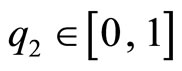). In other words, firm 2 does not need new knowledge to produce the product given in (17).

2)    If firm 1 does not invest in R&D:

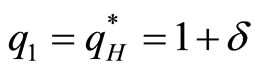(18)

(19)

2.3. First Stage: R&D Decision

Lemma 1: Firm 2 will never invest in its own R&D activity.

Proof: Because firm 2 can produce products given in (17) or (19) with its current knowledge, it does not need any new knowledge. In addition, if firm 2 does not invest in R&D activity, it can save a cost of F.

Now, consider the following:

1)    If firm 1 invests in R&D activity:

Substituting (16) and (17) into (12) and (13), we have profits of both firms as follows:

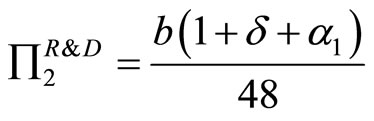(20)

(21)

2)    If firm 1 does not invest in the R&D activity:

Substituting (18) and (19) into (12) and (13), we have profits of both firms as follows:

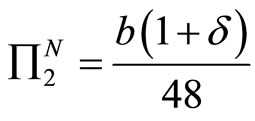(22)

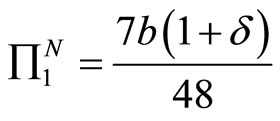(23)

By comparing (21) with (23), we arrive at Lemma 2. We note here that. The parameter 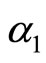measures the level of technology progress when firm 1 carries out the R&D activity.

Lemma 2: Firm 1 will invest in R&D if technology progress 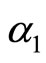is larger than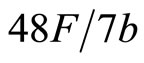. Otherwise it will not invest in R&D.

By comparing (20) with (22), if firm 1 does not invest in R&D, the profit of firm 2 will reduce by an amount of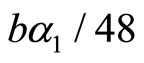. Thus, if firm 2 contributes an amount of money to firm 1 that covers the gap of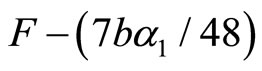, firm 1 will conduct the R&D activity. This will result in both firms being better off. However, if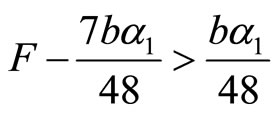, firm 2 will not support firm 1 in the R&D activity. Thus, we come into the following proposition.

Proposition 2: The decisions of the quality leader and follower regarding the R&D activity are dependent on the technology progress:

1)    If the technology progress is large (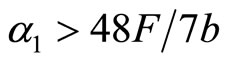), the leader will conduct the R&D by itself;

2)    If technology progress is low (but 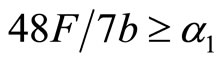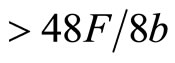) , both firms will cooperate in R&D activity. The motive for the R&D cooperation of the follower is to produce new knowledge for the leader;

3)    If technology progress is very low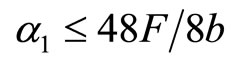, both firms will not invest in the  R&D activity.

Case b of proposition 2 gives the interesting implication that the low quality firm has an incentive to cooperate with the high quality firm to induce R&D activity in the high quality firm when it accepts its position as a follower. This motive for R&D cooperation of the follower is purely related to the quality ‘location’ of its products.

3. Empirical Implication

We have shown that a rival leader and follower have an incentive to cooperate. Both parties feel this incentive, as their products can increase in quality, and hence the utility and the price consumers will be willing to pay increases. We thus see the realized net result of such cooperation as producing no net change in the overall market structure. Given the assumptions we noted in the development of our model, we believe the potential for this kind of “bottom-up” initiated R&D cooperation between competitors can be realized.

Since it may seem counterintuitive that a follower should assist an industry leader, the existence of R&D cooperation as we have modeled may be underrepresented in the range of decisions that might be contemplated by competitors. What we might expect to see considered is a more intuitively appealing “reciprocity”. For example, rather than a transfer of funds gratis, we might to see agreements for cooperation in which one firm agrees to fund R&D while the other agrees to transfer new knowledge in return. When this occurs, it might not be obvious to the researcher that cooperation was initiated from below, or that the reciprocal nature of the agreement was not even necessary for both parties to accrue benefit.

Proposition 2b of our model shows that in the instance where cooperation is favored, the follower just assists the leader to gain normal profit from R&D activity. Thus, the additional gain of the follower is more than that of the leader. This suggests a way that the researcher can distinguish between an agreement that is truly reciprocal and one that is the result of the less than altruistic motive we described. If the cooperation is truly reciprocal, we might expect such agreements to be equally initiated from above as well as from below. However if the cause and effect are as we propose, we would expect to see agreements to cooperate initiated more often from below than from above.

The motive for cooperative behavior among rivals as we have described will not, of course, exist in situations where a quality leader maintains exclusive or strict proprietary product rights that affect a follower’s ability to advance within the quality range we have specified. But in our assumptions, we regarded the each firm’s capability to select the quality level as current internal knowledge of the firm. For the follower, this meant being able to select anywhere within the range 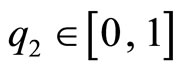meaning its advancement is unrestrained in this region. If, for example, a production method is proprietary by the leader, one still could imagine the case where a rival can advance by using an alternative methodology. Our Lemma 1 indicates the follower can produce products in (17) or (19) given its current knowledge – so our model applies in the realm where propriety rights have no impact on the movement of the follower, if such rights exist. Furthermore, if we observe a leader initiating and maintaining proprietary rights for the new knowledge resulted from R&D cooperation, it will be obvious that our model is at work.

4. Conclusions

Our theoretical model has revealed that there may exist a novel motive for R&D cooperation between a quality follower and a rival quality leader. We have demonstrated that when a firm accepts its position of the follower, it has an incentive to support the leader to increase the leader’s product quality as it can subsequently select a better quality ‘location’ for its product. Furthermore, we have shown, under the conditions we define in this paper, that the follower’s underlying motive for R&D cooperation is not for new knowledge.

While our model has shown a special motive for R&D cooperation between rivals, empirical studies which show this unambiguously occurring are needed to support this prediction. We believe our model represents a rational decision for competitors, and imagine its potential contribution to welfare as well.

5. References

[1]       W. A. Cohen and D. A. Levinthal, “Innovation and Learning: The Two Faces of R&D,” Economic Journal, Vol. 99, No. 397, 1989, pp. 569-596. doi:10.2307/2233763

[2]       W. A. Cohen and D. A. Levinthal, “Absorptive Capacity: a New Perspective on Learning and Innovation,” Administrative Science Quarterly, Vol. 35, No.1, 1990, pp. 128-152. doi:10.2307/2393553

[3]       B. Cassiman and R. Veugelers, “R&D Cooperation and Spillovers: Some Empirical Evidence from Belgium,” American Economic Review, Vol. 92, No. 4, 2002, pp. 1169-1184. doi:10.1257/00028280260344704

[4]       R. Casadesus-Masanell and D. B. Yoffie, “Wintel: Cooperation and Conflict,” Management Science, Vol. 53, No. 4, 2007, pp. 584-598. doi:10.1287/mnsc.1060.0672

[5]       B. Kogut, “Joint Ventures: Theoretical and Empirical Perspectives,” Strategic Management Journal, Vol. 9, No. 4, 1988, pp. 319-332. doi:10.1002/smj.4250090403

[6]       T. Schmidt, “Motives for Innovation Co-Operation: Evidence from the Canadian Survey of Innovation,” ZEW Discussion Paper, Center for European Economic Research, No. 07-018, 2007.

[7]       X. Wauthy, “Quality Choice in Models of Vertical Differentiation,” The Journal of Industrial Economics, Vol. 44, No. 3, 1996, pp. 345-353. doi:10.2307/2950501

[8]       A. J. Choi and H. S. Shin, “A Comment on a Model of Vertical Product Differentiation,” Journal of Industrial Economics, Vol. 40, No. 2, 1992, pp. 229-231. doi:10.2307/2950513

[9]       L. Beloqui and J. M. Usategui, “Vertical Differentiation and Entry Deterrence: A Reconsideration,” DFAEII Working Papers, Dept. Fundamentos del Analisis Economico II, Universidad del Pais Vasco, WP 2005-06, 2005.

[10]    K. S. Moorthy, “Product and Price Competition in a Duopoly,” Marketing Science, Vol. 7, No. 2, 1988, pp. 141-168. doi:10.1287/mksc.7.2.141

[11]    A. Shaked and J. Sutton, “Relaxing Price Competition through Product Differentiation,” Review of Economic Studies, Vol. 49, No. 1, 1982, pp. 3-13. doi:10.2307/2297136

NOTES

¹See Schmidt (2007) [6].

²See Wauthy (1996) [7] and Beloqui & Usategui (2005) [9].

³See Wauthy (1996) [7] and Beloqui and Usategui (2005) [9].

⁴See Wauthy (1996) [7].