Journal of Electromagnetic Analysis and Applications
Vol.06 No.10(2014), Article ID:50042,9 pages
10.4236/jemaa.2014.610031
Solution of 1D Poisson Equation with Neumann-Dirichlet and Dirichlet-Neumann Boundary Conditions, Using the Finite Difference Method
Serigne Bira Gueye, Kharouna Talla, Cheikh Mbow
Département de Physique, Faculté des Sciences et Techniques, Université Cheikh Anta Diop, Dakar-Fann, Sénégal
Email: sbiragy@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 May 2014; revised 16 June 2014; accepted 11 July 2014
ABSTRACT
An innovative, extremely fast and accurate method is presented for Neumann-Dirichlet and Dirichlet-Neumann boundary problems for the Poisson equation, and the diffusion and wave equation in quasi-stationary regime; using the finite difference method, in one dimensional case. Two novels matrices are determined allowing a direct and exact formulation of the solution of the Poisson equation. Verification is also done considering an interesting potential problem and the sensibility is determined. This new method has an algorithm complexity of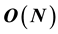 , its truncation error goes like
, its truncation error goes like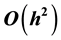 , and it is more precise and faster than the Thomas algorithm.
, and it is more precise and faster than the Thomas algorithm.
Keywords:
1D Poisson Equation, Finite Difference Method, Neumann-Dirichlet, Dirichlet-Neumann, Boundary Problem, Tridiagonal Matrix Inversion, Thomas Algorithm

1. Introduction
Poisson equation is used to describe, in quantitative manner, electrostatic and magnetostatic phenomena. It also helps to understand diffusion and propagation related problems, in quasi-stationary regime. Its solution is of great interest for a wide range of fields such as engineering, physics, mathematics, biology, chemistry, etc.
Most of solving methods, of this very important equation, use matrix inversion technics and algorithms, which are dependent on its Right-Hand Side (RHS). A recent study [1] , concerning the case of one dimension, has proposed a direct, exact, and closed formulation of the inverse matrix; independently on the RHS. This inverse matrix has allowed getting a new, extremely fast solution to the Poisson equation. However, this innovative solution, obtained with the finite difference method, discussed only the case of boundary conditions of type: Dirichlet-Dirichlet (DD).
In the present study, we focus on the Poisson equation (1D), particularly in the two boundary problems: Neumann-Dirichlet (ND) and Dirichlet-Neumann (DN), using the Finite Difference Method (FDM). Essentially, attention is given to the matrices extracted from the algebraic equations from this differential method. Furthermore, an exact formulation of their inverses, independently of the RHS, is determined. Therefore, a new and advanced formulation of the solution to the Poisson equation, is found, for Neumann boundary conditions.
The proposed method is more accurate and faster than the Gaussian elimination method and that of Thomas. In addition, it completes the work made by Gueye S. Bira [1] , where the Dirichlet-Dirichlet problem was presented and treated very rigorously and clearly. Here, we determine two matrices that constitute, with the one in ref. [1] , a set of solutions, which will contribute greatly to the advance of research in the field of numerical solving of differential equations. They will also permit an extremely exact and simple formulation of the solution to the Poisson equation.
We will first consider an ND boundary problem and establish the corresponding algebraic equations coming from the application of the finite difference method, using the centered difference approximation (second order derivative). Then, we will, based on these algebraic equations, and considering the boundary conditions; establish the matrix equation. Thereafter, we discuss the properties of the associated matrix and then, determine its inverse, exactly and independently of the RHS. This will allow a direct and exact formulation of the solution to the Poisson equation for a 1D problem with ND boundary conditions. Complexity, accuracy, and stability are discussed and compared with other methods: Gaussian elimination algorithm and Thomas. Moreover, a verification of this new method is done by considering an interesting potential problem with inhomogeneous ND boundary conditions. The results are compared to the exact analytical solution and show great agreement. A similar approach is followed in the case Dirichlet-Neumann problem. The exact formula of the inverse matrix is determined and also the solution of the differential equation.
2. 1D Poisson Equation with Neumann-Dirichlet Boundary Conditions
We consider a scalar potential 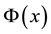 which satisfies the Poisson equation
which satisfies the Poisson equation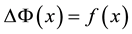 , in the interval
, in the interval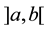 , where
, where 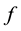 is a specified function.
is a specified function. 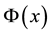 fulfills the Neumann-Dirichlet boundary conditions
fulfills the Neumann-Dirichlet boundary conditions
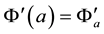 and
and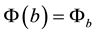 . An appropriate discretization is chosen, as shown in Figure 1.
. An appropriate discretization is chosen, as shown in Figure 1.
The mesh is composed of 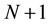 discrete points belonging to the interval
discrete points belonging to the interval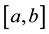 ; and an extra, imaginary
; and an extra, imaginary
point, 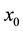 , which is not within this range [2] [3] . With the following step size:
, which is not within this range [2] [3] . With the following step size: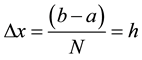 , the mesh points
, the mesh points 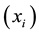 are defined by the following relation:
are defined by the following relation: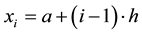 ,
,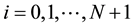 . We denote by
. We denote by 
proximate value of the desired potential at point










and the second derivative:
Figure 1. Discretization for Neumann-Dirichlet boundary conditions.

Thus, the discretized 1D Poisson equation becomes a set of algebraic equations:

The boundary 



One sees that this extra point does not affect the result. It is also to remark that the truncation error goes like 

We can introduce the vector 


Thus, one obtains the following matrix equation:

The centered difference approximation leads to an N × N-matrix 
3. The Inverse of the Matrix
The inverse of the matrix


where 
It also holds:

The behavior of the determinant and the co-factor of the matrix 

Using the relations in (7)-(9), we can determine exactly the inverse of the matrix 


Equation (10) is also equivalent to:

Equations (10) and (11) contain the same information. We prefer the first because it appears to be simpler than the latter and can be preferred for an eventual implementation in a programming language.
Thus, the inverse matrix is entirely determined. We get the simple, beautiful, exact, and very important matrix 
We call this impressive matrix

4. Analysis and Exact Solution of the Poisson Equation
The matrix 



With Equation (6), one obtains the solution 


The scalar potential 


Thus, the solution of the 1D Poisson equation, in the case of Neumann-Dirichlet boundary, is determined exactly with the direct relation:

This is equivalent to:

Figure 2. Inverse matrix for Neumann-Dirichlet problem.
Equation (15) represents a great improvement for solving the Poisson equation, particularly for Neumann- Dirichlet boundary conditions. The solution is determined properly, exactly, and given in a direct formulation. It can be very easily programmed. One loop will be largely sufficient to compute all the solution of one the most important equation in physics and engineering, in the one-dimensional case. It is a novel and exact formulation of the solution with the finite difference method using the centered difference approximation. The very important matrix 
The methods that use inversion technics to obtained the matrix 


The presented new solution is more direct, more exact, more stable; and faster than the Thomas Method for 1D Poisson equation. An important fact is that the determination of 
5. Verification with a Neumann-Dirichlet Potential Problem
We consider a scalar field

in









We can apply the finite difference method, taking:











Then, we compute the solution, with new method, given by Equation (15) and compare it with the exact potential (Equation (16)). Naturally, we also take into account the Equation (5).
We denote by 





For a given

The denote 


It is calculated for the given parameters and its value is:
Table 1 illustrates the potential

Table 1. Results of the Neumann-Dirichlet problem..
the centered approximation. It also gives the exact value of the potential

We see that the solution of the ND boundary problem with the proposed method is also very accurate as shown in the table above.
At this stage, we are interested in the sensitivity of this method. We have shown the average relative error 

tion can be assumed to be proportional to
A curve fitting of the sensibility can be given with:

where
The average relative error 





For the given function 

6. Solution of Dirichlet-Neumann Problem
6.1. Discretization and Matrix Equation
As we proceeded in the case of boundary conditions of type ND; we will do the same for a DN problem. The first step is to find an adequate and comfortable discretization. We propose that of Figure 4.
Figure 3. Sensibility for the Neumann-Dirichlet problem.
Figure 4. Discretization for Dirichlet-Neumann boundary conditions.
Here, the mesh points 







Thus, the vector 

Thus, the matrix equation becomes:

In the case of DN boundary conditions, the matrix 

6.2. Inverse Matrix and Closed Solution
Thus, the inverse matrix of 
We call this impressive matrix

This solution, given by the simple and extremely important Equation (24), can be easily computed, in one programming loop that give all the solutions.
7. Verification with a Dirichlet-Neumann Boundary Problem
We consider the same potential as that of the ND boundary problem, studied above. In this DN problem, the
boundary conditions are: 



We can apply the finite difference method, taking:











Then, we compute the solution, of our new method, given by Equation (24) and compare it with the exact potential.
Table 2 shows the obtained results:
The solution of the DN problem is also very accurate as shown in Table 2:

Table 2. Results of the Dirichlet-Neumann problem.
Figure 5. Inverse matrix for Dirichlet-Neumann problem.
Figure 6. Sensibility for the Dirichlet-Neumann problem.
Now, the sensibility can be determined, for the DN boundary problem: the average relative error 


A curve fitting of the sensibility can be given using Equation (20) with
The average relative error 

8. Conclusion
This study has determined two novels matrices independently of the RHS providing a new and exact formulation of the solution of the Neumann boundary problem, for the 1D Poisson equation. The presented results and methods constitute a great improvement in the field of solving similar equations: diffusion and wave equations, in the quasi-stationary case, using the FDM. They are direct, highly accurate, extremely fast, and economical in terms of memory occupation.
References
- Gueye, S.B. (2014) The Exact Formulation of the Inverse of the Tridiagonal Matrix for Solving the 1D Poisson Equation with the Finite Difference Method. Accepted Manuscript (JEMAA, April 2014).
- Engeln-Muellges, G. and Reutter, F. (1991) Formelsammlung zur Numerischen Mathematik mit QuickBasic-Program- men, Dritte Auflage, BI-Wissenchaftsverlag, 472-481.
- Kreiss, H.O. (1972) Difference Approximations for Boundary and Eigenvalue Problems for Ordinary Differential Equations. Mathematics of Computation, 26, 605-624. http://dx.doi.org/10.1090/S0025-5718-1972-0373296-3
- LeVeque, R.J. (2007) Finite Difference Method for Ordinary and Partial Differential Equations, Steady State and Time Dependent Problems. SIAM, 15-16. http://dx.doi.org/10.1137/1.9780898717839
- Conte, S.D. and de Boor, C. (1981) Elementary Numerical Analysis: An Algorithmic Approach. 3rd Edition, McGraw- Hill, New York, 153-157.
- Mathews, J.H. and Fink, K.K. (2004) Numerical Methods Using Matlab. 4th Edition, 323-325, 339-342.









