Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 6 (2011) , Article ID: 5610 , 5 pages DOI:10.4236/jemaa.2011.36034
Characterization and Optimization of Photonic Crystal Optical Power Limiters
![]()
Departament of Multidisciplinary Study, University of Guanajuato, Guanajuato, Mexico.
Email: guryev@ieee.org
Received March 6th, 2011; revised April 1st, 2011; accepted May 2nd, 2011.
Keywords: Nonlinear Photonic Crystal, Optical Power Limiter, Kerr Nonlinearity
ABSTRACT
In the work, there have been investigated the optical power limiting effects which occur in the nonlinear photonic crystals possessing saturable Kerr nonlinearity. The method is proposed which allows exact determination of the parameters of the structure as well as the radiation parameters which provide the limiting effect.
1. Introduction
Today, one of important problems in optical communications and information processing is development of effective optical power limiter on the basis of structures with periodic modulation of refractive index. Such a problem is formulated, particularly, in [1]. Earlier, the utilization of nonlinear Cristiansen filters [2] as well as anisotropy induction in organic liquids [3] were proposed as optical power limiting devices. Particularly, there are ideas based on the effect of appearance of Bragg grating at high level radiation intensity inside structures having initially uniform refractive index distribution [4]. Such devices are represented by some kind of layered structure with layers’ refractive indices initially equal. Layers are made of nonlinear materials with different nonlinearity coefficient so as the radiation intensity passing the structure increases, different variation of layers’ refractive indices appear. Due to this effect, the step-index (or any other periodic) structure appears. This can cause, at certain conditions, the limitation of optical radiation power at the output of such structure.
In our work we investigated the possibility of the development of an optical power limiter based on the variation of reflectance spectrum of nonlinear PhC with Kerr-nonlinearity under the intense optical radiation. It is also given an analytical expression of necessary reflectance spectrum form. Moreover, we made an approximation of reflectance spectrum by the obtained analytical function and gave the parameters’ values for 1D and 2D PhCs. After this, the dependences of the output radiation intensity on the input one were given for these cases. Numerical results approve proposed theoretical model.
2. Theory
The main function of an optical power limiter is to stabilize an intensity 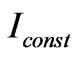 of an optical radiation. As an input data for this task there is the structure which reflectance depends on the radiation intensity. The task itself consists in the obtaining of the parameters of the structure, the wavelength and the intensity range of the radiation that will provide the stabilization of the radiation intensity at certain level
of an optical radiation. As an input data for this task there is the structure which reflectance depends on the radiation intensity. The task itself consists in the obtaining of the parameters of the structure, the wavelength and the intensity range of the radiation that will provide the stabilization of the radiation intensity at certain level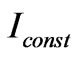 .
.
Let’s represent 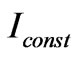 as a radiation intensity passing the structure without absorption. At that
as a radiation intensity passing the structure without absorption. At that 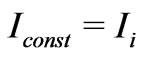
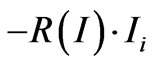 , where
, where 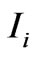 is the radiation intensity that incidents the structure. Thus, the passing radiation intensity will be incident intensity minus reflected intensity.
is the radiation intensity that incidents the structure. Thus, the passing radiation intensity will be incident intensity minus reflected intensity.
This expression gives the dependence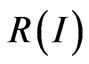 :
:
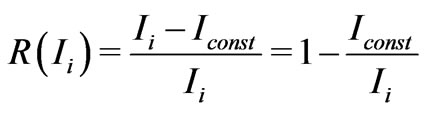 (1)
(1)
In the Figure 1 it is shown the set of curves for different values of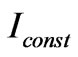 . By dashed lines it is shown the cross-point between the function and intensity axes. As it is seen, when the parameter
. By dashed lines it is shown the cross-point between the function and intensity axes. As it is seen, when the parameter 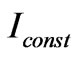 varies, coordinate of the cross-point varies too as well as the slope of the function. Thus, the variation of the reflectance in this way will result in the stabilization of the radiation intensity.
varies, coordinate of the cross-point varies too as well as the slope of the function. Thus, the variation of the reflectance in this way will result in the stabilization of the radiation intensity.
It is now necessary to find the dependence of the reflectance on the intensity for the case of nonlinear PhC
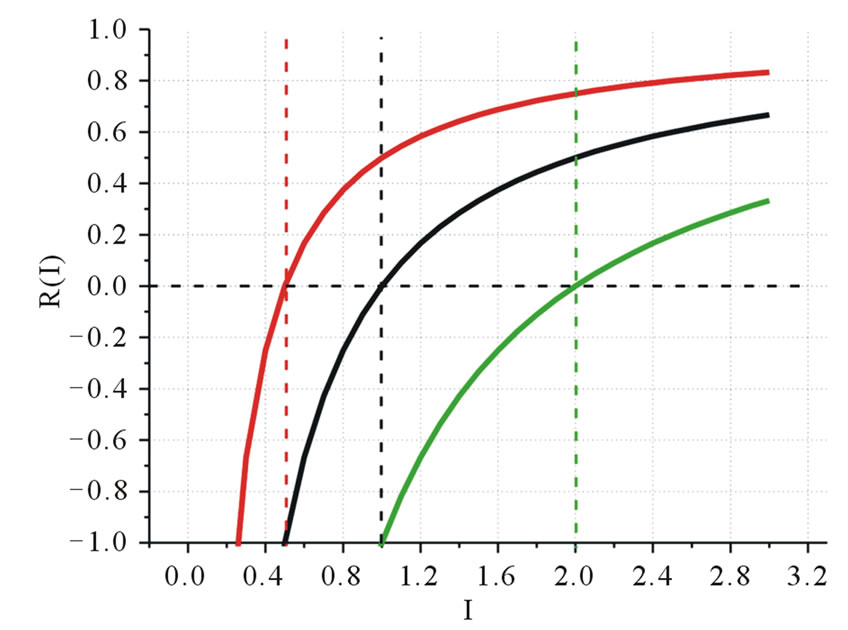
Figure 1. A set of predicted analytical curves of the dependence of reflectance on the radiation intensity.
that will be approximated by the analytical function as good as possible.
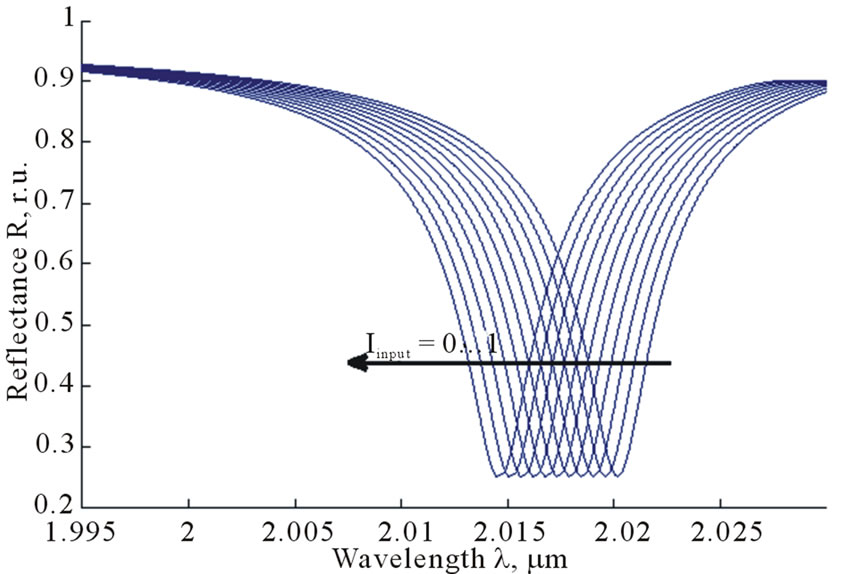
In the work [5] it have been investigated reflectance spectra as well as dependences of the reflectivity of nonlinear 1D PhC on the radiation intensity at different wavelengths. It has been shown that, at certain conditions, monotonicy of 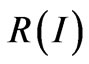 dependence can be broken. At that, local extremum appears. The set of
dependence can be broken. At that, local extremum appears. The set of 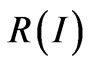 dependences at different wavelengths is shown in Figure 2.
dependences at different wavelengths is shown in Figure 2.
In order to obtain a maximum fit of the function, it is necessary to vary the parameter 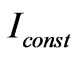 in the expression (1). Moreover, we can use the fact that
in the expression (1). Moreover, we can use the fact that 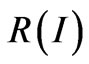 shape depends on the reflectance spectrum shape as it was shown before.
shape depends on the reflectance spectrum shape as it was shown before.
Thus, the fitting procedure requires the determination of two parameters. The first one is the placement of point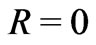 . This parameter determines the operating wavelength. The second parameter is
. This parameter determines the operating wavelength. The second parameter is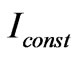 , which means the Consequently, the parametric function has the following
, which means the Consequently, the parametric function has the following
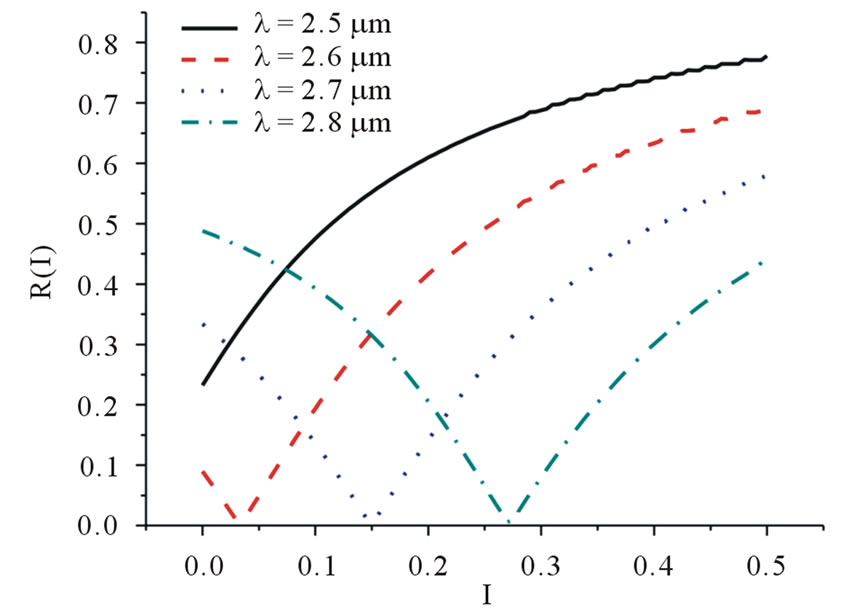
Figure 2. The dependence of the reflectivity of nonlinear 1D PhC at different wavelengths.
form:
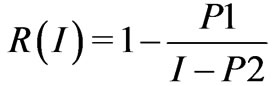 , (2)
, (2)
where P1 is the parameter varying the shape and the displacement of the analytical function and P2 is the parameter that allows to determine the correction of the wavelength.
3. 1D Optical Power Limiter
For the correct automatic parameters fitting it is necessary to approach the view of the curve under approximation to the analytical one as good as possible. In our case the procedure consists in elimination of all points to the left of the point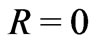 .
.
Fitting for the numerical results at wavelength 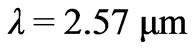 we obtain the following parameters’ values: Р1 = 0.20088, Р2 = –0.19036.
we obtain the following parameters’ values: Р1 = 0.20088, Р2 = –0.19036.
The P2 parameter indicates that the function is shifted on the intensity axis 0.19036 to the left from necessary point. The Figure 2 shows that increasing the wavelength we can expect to have the 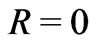 point at necessary place.
point at necessary place.
After the second fitting we have the following parameters’ values: Р1 = 0.27593, Р2 = –0.0495. Changing the wavelength one more time by the value 0.0495 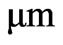 and carrying out the fitting procedure one more time at
and carrying out the fitting procedure one more time at 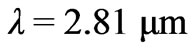 we obtain final values of parameters: Р1 = 0.2942, Р2 = –0.00741. (see Figure 3)
we obtain final values of parameters: Р1 = 0.2942, Р2 = –0.00741. (see Figure 3)
Thus, we obtained almost full agreement between results of numerical modeling and obtained analytical function. The approximation error is less than 0.1% Thus, the device with such parameters will be able to stabilize the radiation at level 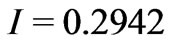 of normalized intensity.
of normalized intensity.
Let us investigate the characteristics of the device presented in Figure 4. At the level of the incident radiation
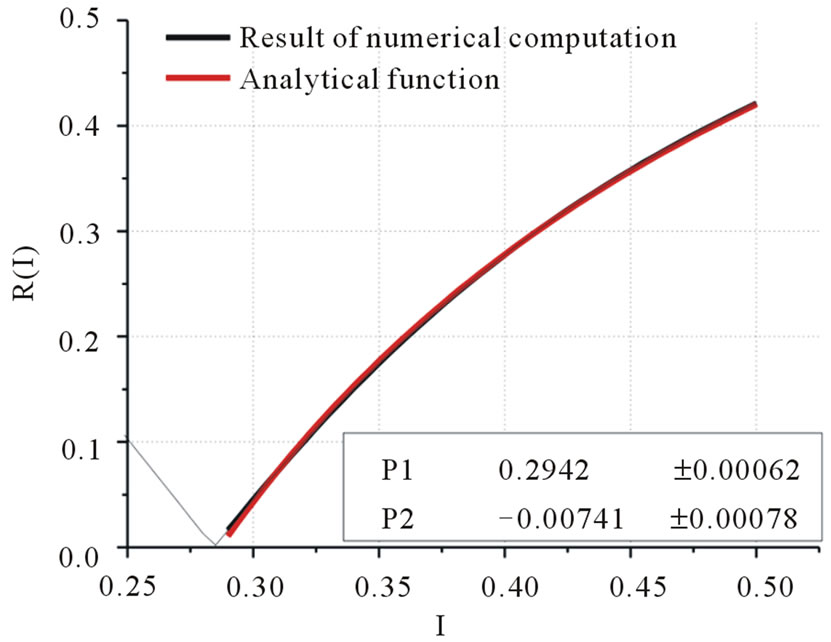
Figure 3. Results of the final approximation attempt.
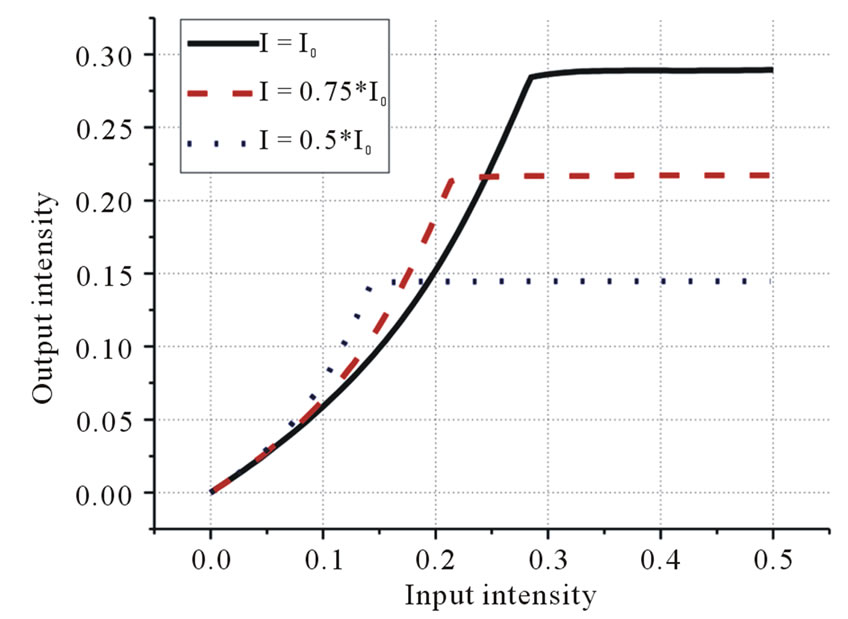
Figure 4. The dependences of the output radiation intensity on the input one for different levels of stabilized intensity.
intensity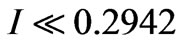 , the reflectivity of the structure is higher than zero. When the radiation intensity reaches the value of
, the reflectivity of the structure is higher than zero. When the radiation intensity reaches the value of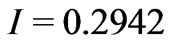 , the reflectivity of the structure becomes zero providing output radiation intensity level
, the reflectivity of the structure becomes zero providing output radiation intensity level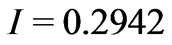 . Further increasing of the intensity will result in growing of the reflectance of the structure. Previously we found the reflectivity on intensity function that provides constant output radiation intensity. Thus, within the limits considered in the work (from
. Further increasing of the intensity will result in growing of the reflectance of the structure. Previously we found the reflectivity on intensity function that provides constant output radiation intensity. Thus, within the limits considered in the work (from 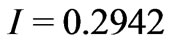 to
to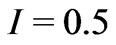 ), the device stabilizes radiation intensity at level
), the device stabilizes radiation intensity at level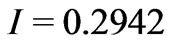 .
.
Earlier we have shown the possibility to stabilize the radiation intensity at level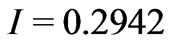 . This means that the function
. This means that the function 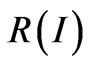 has the following form:
has the following form:
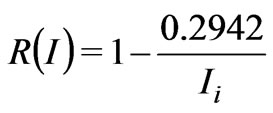 (3)
(3)
However, it is necessary to mention that at the intensity axis lays normalized intensity 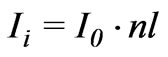 and the expression (3) which approximates computed curve, have the nonlinearity coefficient equal to 1. If it is necessary to stabilize any other value of intensity, we can vary nonlinearity coefficient of the material and, as a result, will have the same dependence. For instance, let’s consider the stabilization of the intensity at level
and the expression (3) which approximates computed curve, have the nonlinearity coefficient equal to 1. If it is necessary to stabilize any other value of intensity, we can vary nonlinearity coefficient of the material and, as a result, will have the same dependence. For instance, let’s consider the stabilization of the intensity at level 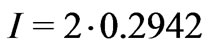 i.e. two times larger than previous value.
i.e. two times larger than previous value.
For this reason, it is necessary to multiply nonlinearity coefficient by two. As a result, we’ll have the following expression:
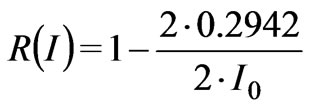 (4)
(4)
Nonlinearity coefficient in the expression (3) was equal to 1 and no it is equal to 2.
Therefore, once obtained curve allows finding parameters for any nonlinearity coefficient of the structure.
The tuning of the device operating wavelength can be carried out by the scaling of the geometric parameters of the device as well as refractive indices of the layers.
4. 2D Optical Power Limiter
In case of optical power limiter on the basis of 2D PhC main principles of the functioning are the same as previously. Therefore, it is necessary to determine the PhC and the radiation parameters at which the dependence of the structure on the radiation intensity will be described by the expression (1).
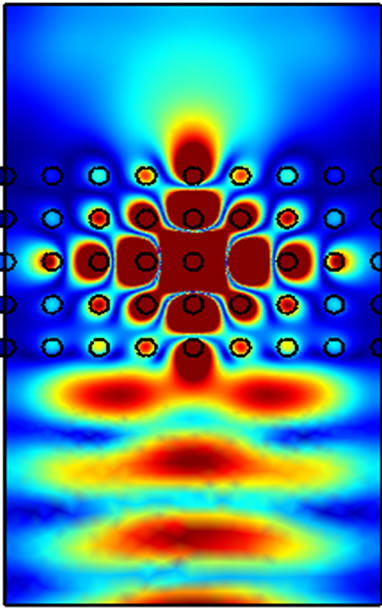
The 2D structure of the power limiter considered in the work is represented by the uniform PhC containing one nonlinear rod made of saturable Kerr-nonlinear material. Material parameters are taken the same as in the work [5]. The field distribution within the filter computed at low and high radiation intensity is presented in the Figure 5.
When investigating 2D PhC, we have considered two different types of nonlinear PhC. Namely, with high and low nonlinearity saturation threshold.
In order to obtain necessary PhC parameters, the reflectance spectra at different radiation intensity levels were computed near one of the local minima (see Figure 6). It should be mentioned that in both cases the spectrum appears to be blue-shifted with the growth of radiation intensity. However, in case of high saturation threshold, the shift of the peak is almost linear while in case of low threshold, the shift is almost absent when the radiation intensity approaches the threshold value.
As in case of 1D PhC, for the determination of PhC and the radiation parameters it have been computed the set of characteristics describing the dependence of the structure reflectance on the radiation intensity at different wavelengths (see Figure 7). Each characteristic possesses
 (a)
(a)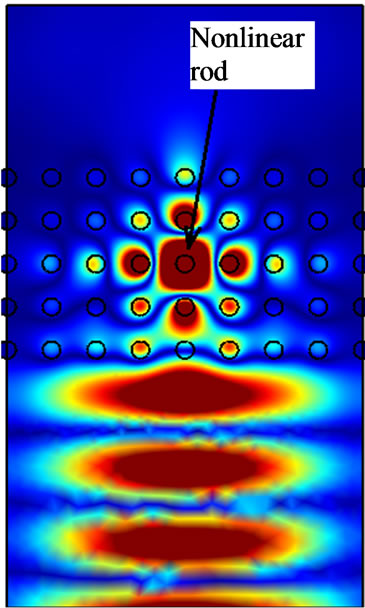 (b)
(b)
Figure 5. Field distributions inside the PhC filters with nonlinear rod at low (a) and high (b) intensity.
 (a)
(a)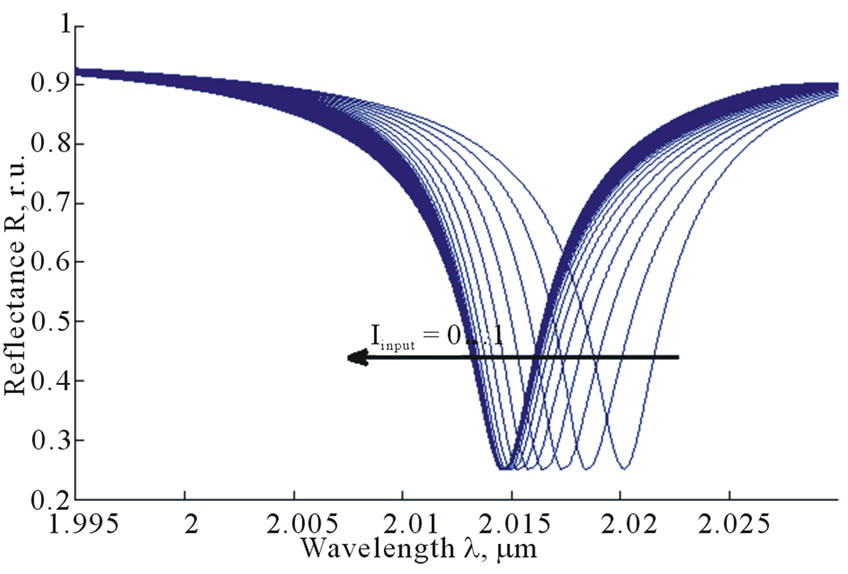 (b)
(b)
Figure 6. Field distributions inside the PhC filters with nonlinear rod at low (a) and high (b) intensity.
local extremum at specific value of the radiation intensity similar to those in Figure 2. The radiation intensity, at which the minimum of the reflectance is achieved, strongly depends on the wavelength and, therefore, varying the radiation wavelength we can vary the position of the function on the intensity axis.
In contrast to the 1D PhC case, it was impossible to find the radiation parameters which eliminate the value of P2 from the parametric Equation (2). However, the P2 parameter has also physical meaning. If, for instance, we consider the structure with some auxiliary light source (in case of negative P2) or the structure with constant absorption (positive P2), the parametric Equation (2) makes sense even with non-zero P2. With this, in order to obtain the constant output radiation intensity, we only need one more element in addition to the input light source.
Results of approximation of numerical results by the analytical function (2) are shown in Figure 7. The approximation error is less than 5% within the investigated intensity ranges.
As it have been shown during the approximation (see the results in the Table 1), each of the obtained characteristics provides power limiting at different wavelengths and at different value of the output radiation intensity. The only condition at which the parameter P2 turns to zero is the case of high saturation threshold at the wavelength l = 2.01824 mm. This means, the limitation in this
 (a)
(a)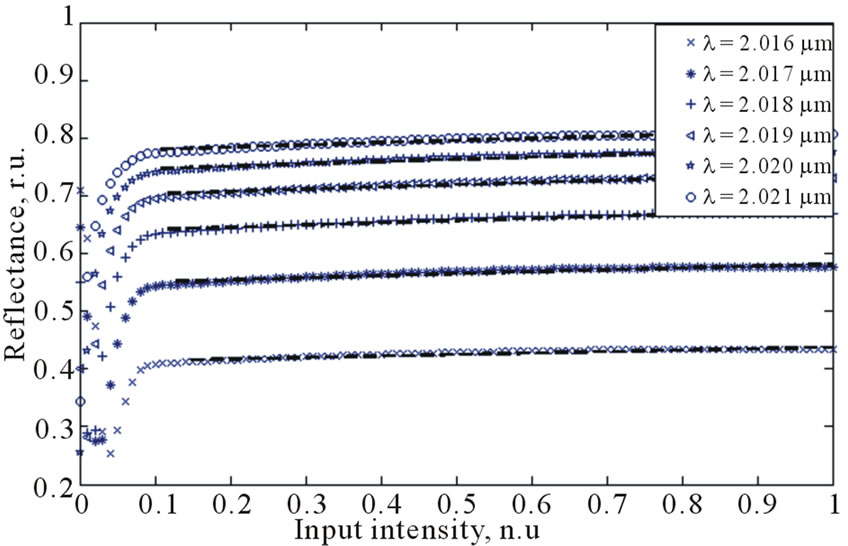 (b)
(b)
Figure 7. Dependence of the reflectance of the 2D structure on the intensity at different wavelengths in case of high (a) and low (b) saturation threshold.
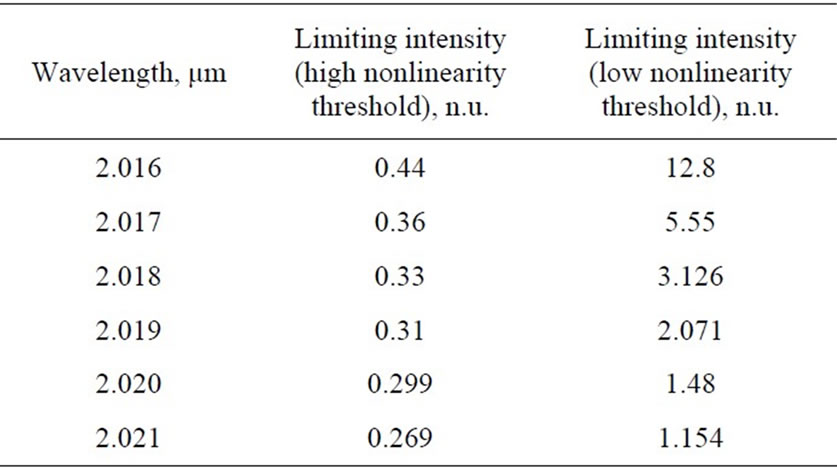
Table 1. The wavelength and corresponding radiation intensities satisfying the parametric Equation (2) in case of high and low nonlinearity saturation threshold.
case is possible without additional absorber or light source.
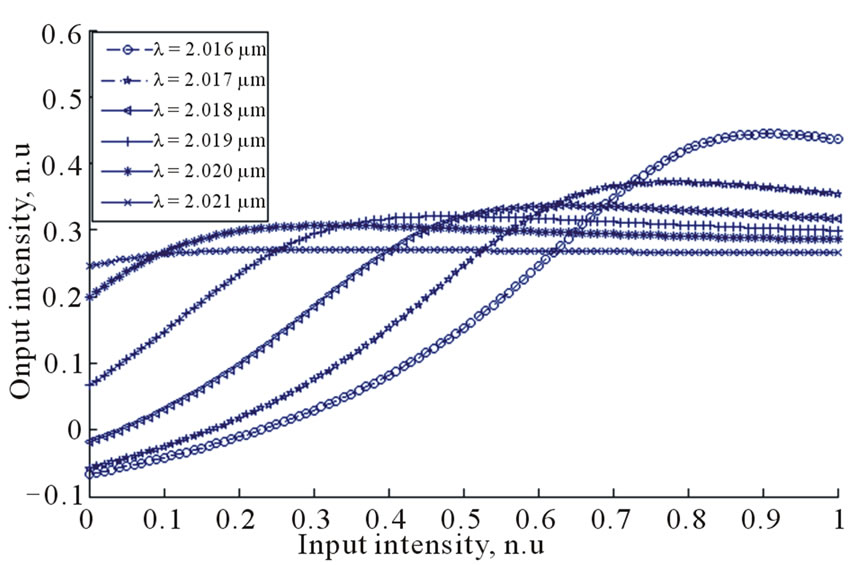
To prove the obtained results, the output radiation intensity has been computed as a function of the input radiation intensity for each of considered cases by means of the FEM-iterative method. In Figure 8 it is shown the computation results. As is seen, in all the cases, the radiation is stabilized at the specific value predicted by the approximation results earlier.
The tunability of the results obtained by the proposed method is provided by the scaling properties of the PhC. However, such scalability is limited by the material characteristics such as dispersion of the linear and nonlinear parts of the refractive index. In this case, one may need several iterations of the investigation process to achieve desired wavelength and intensity levels.
5. Conclusions
In the work it have been investigated 1D and 2D periodic structures including elements demonstrating Kerr-
 (a)
(a)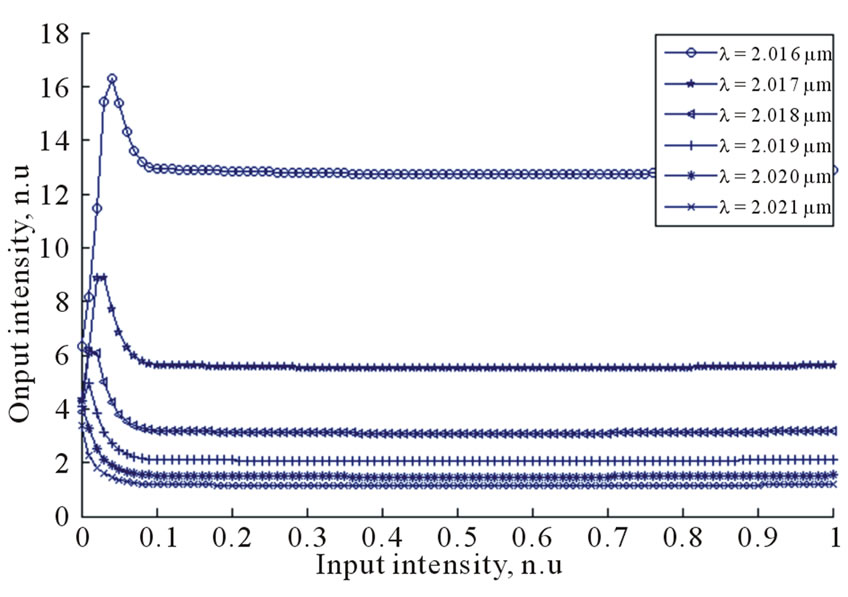 (b)
(b)
Figure 8. Results of the final approximation for 2D structure in case of high (a) and low (b) saturation threshold.
nonlinearity. There were obtained spectra of devices on the basis of such PhCs at low and high levels of the radiation intensity.
It have been also investigated the possibility of the development of the device stabilizing the radiation intensity at certain level. The reflectance spectrum shift due to the radiation intensity was used to demonstrate the optical power limiting effect. Obtained analytical dependence has quite good agreement with numerical modeling results for 1D PhC obtained in previous work which gives high accuracy of the stabilization of the output radiation intensity within the limits considered in the work. The essential spectrum shift has been also found in case of 2D PhC containing nonlinear element. In this case, there have been also demonstrated the possibility of radiation intensity stabilization both in case of high and low saturation threshold which makes power limiting a matter of the correct PhC parameters selection.
Therefore, due to the possibility of essential real-time characteristics tuning, devices on the basis of nonlinear PhCs can be used in wide spectrum of scientific and technical applications such as high-density packaging active elements of all-optical information processing circuits, active and passive components of all-optical networks, sensors for environment control, sensors for security systems for purpose of detecting of explosives, weapons, and technological sensors for identification of defected products.
REFERENCES
- S. F. Mingaleev and Y. S. Kivshar “Nonlinear Transmission and Light Localization in Photonic-Crystal Waveguides” Journal of the Optical Society of America B, Vol. 19, No. 9, 2002, pp. 2241-2249.
- G. L. Fischer , R. W. Boyd, R. T. Moore and J. E. Sipe, “Nonlinear-Optical Christiansen Filter as an Optical Power Limiter,” Optics Letters, Vol. 21, No. 20, 1996, pp. 1643-1645. doi:10.1364/OL.21.001643
- Y. Huang, G. Siganakis, M. Moharam and S.-T. Wu “Broadband Optical Limiter Based on Nonlinear Photo Induced Anisotropy in Bacteriorhodopsin Film,” Applied Physics Letter, Vol. 85, No. 22, 2004, pp. 5445-5447. doi:10.1063/1.1828590
- L. Brzozowski and E. H. Sargent, “Optical Signal Processing Using Nonlinear Distributed Feedback Structures,” IEEE Journal of Quarterly Electron, Vol. 36, No. 5, 2000, pp. 550-555. doi:10.1109/3.842096
- I. V. Guryev, O. V. Shulika, I. A. Sukhoivanov and O. V. Mashoshina, “Improvement of Characterization Accuracy of the Nonlinear Photonic Crystals Using Finite Elements-Iterative Method,” Applied Physics–B: Lasers and Optics, Vol. 84, No. 1-2, 2006, pp. 83-87.

