Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 2 (2011) , Article ID: 4127 , 4 pages DOI:10.4236/jemaa.2011.32011
Comparative Analysis of Parabolic Bootlace Lens and Conventional Lens Approach
![]()
Microwave Laboratory, Department of Electronics, Madhav Institute of Technology & Science, Gwalior, India.
Email: kushwah.ravipratapsingh@rediffmail.com
Received January 10th, 2011; revised January 26th, 2011; accepted February 1st, 2011.
Keywords: Rotman Lens, Circular focal arc Parabola Multiple beam forming, Bootlace Lens
ABSTRACT
In this paper, parabolic refocusing lens is designed for the same requirements as Rotman lens. Comparison of results obtained with the parabolic refocusing lens with those obtained for the Rotman lens is also given.
1. Lens Geometry
Figure 1 shows the cross-section of a trifocal Parabolic refocusing lens [1]. One focal point F0 is located on the central axis, and two others F1 and F2 are symmetrically located on either side on a parabolic focal arc. Outer contour I2 is a straight line and defines the position of the radiating elements. I1 is the inner contour of the lens (also called the array contour). TEM mode transmission lines W(N) connect the inner and outer contours. Two off axis focal points F1and F2 are located on the focal arc, and makes anglesb, 0 and –b with the X-axis when feeds are placed at F1 , F0 and F2 respectively.
A ray originating from F1 may reach the wave front through a general point P(X,Y) on the inner contour I1, transmission line W(N) and point Q(N) on the outer contour ,and then trace a straight line at an angle –α and terminate perpendicular to the wave front .Also the ray from F1 may reach the wave front from F1 to the point O1, and then through transmission line W(0) to the wave-front. Similarly rays from other feed points may reach their respective wave-front.
Inner contour and the transmission lines are designed from the design equations, which are derived using the fact that, at the wave front, all the rays must be in phase independent of the path they travel. This requires that the total phase shift in traversing the path to reach the wave front in each case be equal. Using this concept and referring [2] to figure 1 following design equations are written:
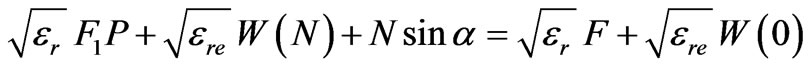 (1)
(1)
 (2)
(2)
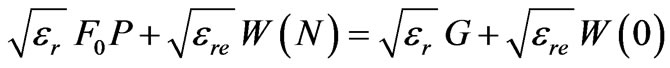 (3)
(3)
where,
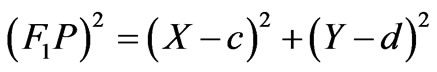 (4)
(4)
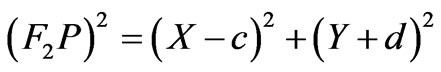 (5)
(5)
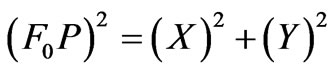 (6)
(6)
F = Distance from point O1 to F1 called the off axis focal length.
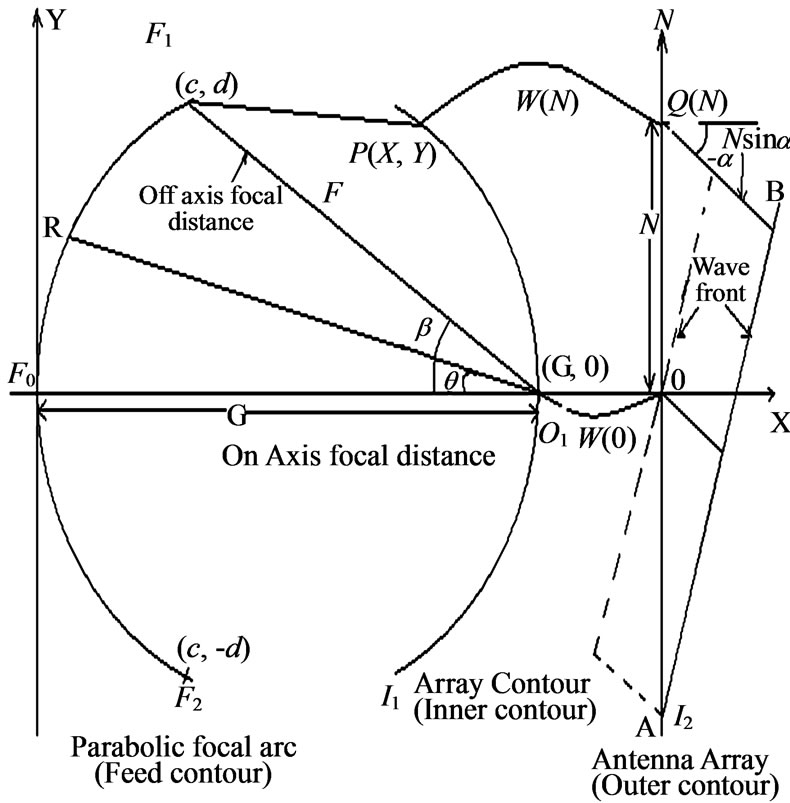
Figure 1. Parabolic Lens Design Geometry.
G = Distance from point O1 to F0 called the on axis focal length.
d = F sinb (Ycoordinate of point F1)
c = G – F cosb (Xcoordinate of point F1)
N = Indicate the position of the radiating elements, called the lens aperture.
er = Substrate dielectric constant.
ere = Effective dielectric constant of the transmission lines.
Design parameters are normalized relative to the maximum lens aperture Nmax and defined as follows:


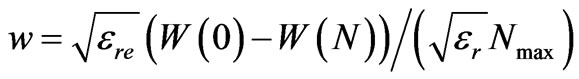

 and
and

From Equation (4)
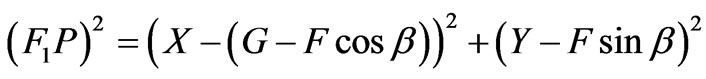
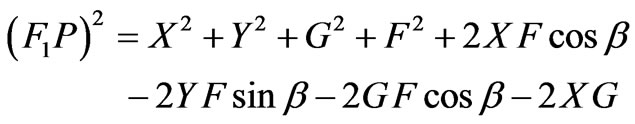
Normalizing w.r.t Nmax
 (7)
(7)
Similarly
 (8)
(8)
From Equation (1)
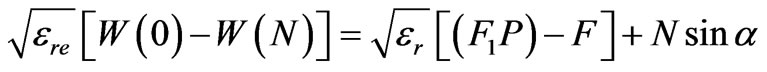
Dividing above Equation by 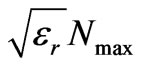
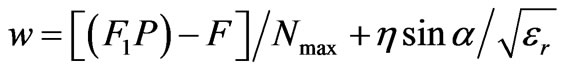 (9)
(9)
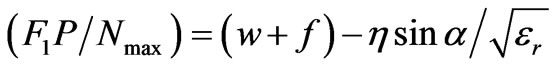 (10)
(10)
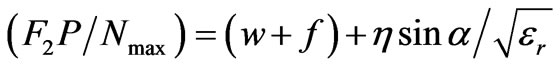 (11)
(11)
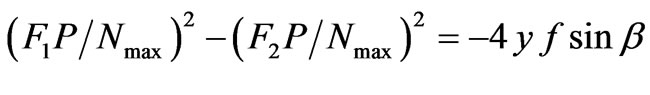
Solving for y we get
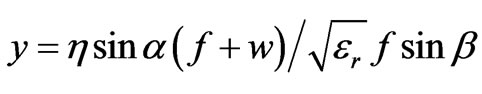 (12)
(12)
From Equation (3)
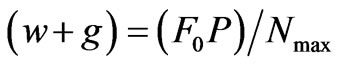
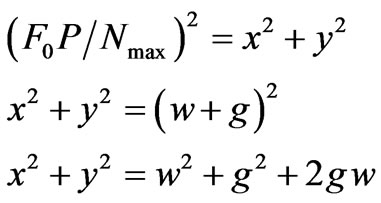 (13)
(13)
By equating value of  with Equation (10)
with Equation (10)

Similarly for 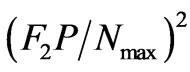 with Equation (11)
with Equation (11)
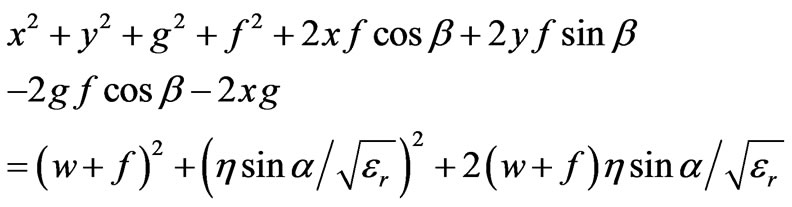
Adding above two Equations

Putting value of  from Equation (13)
from Equation (13)
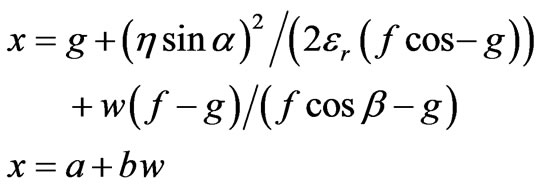 (14)
(14)
where

From Equation (13)

Putting the value of x and y in above equation We get equation in form
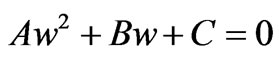 (15)
(15)
where
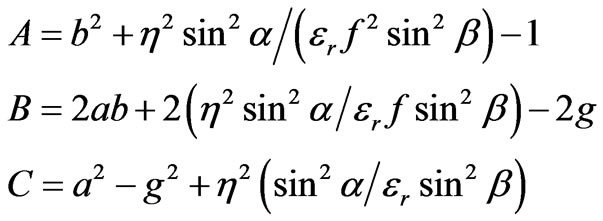
For the given value of design parameters F, G, Nmax and a it is required to calculate the value of b, such that the height of the two contours (feed and array contour) be equal. Y coordinate of array contour is given by Equation (12). For maximum value of lens aperture i.e.
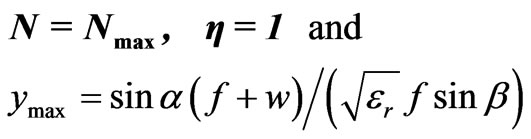 (16)
(16)
To equalize the height of the two contours Y coordinate of the feed contour i.e. f sinb must be equal to ymax i.e.
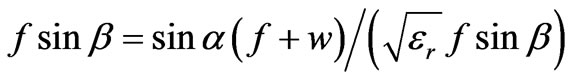 (17)
(17)
Substituting the value of w and h we get X and Y. This completes the design of a trifocal parabolic focal arc bootlace lens.
The relations give the coordinates of the focal arc:
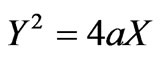
where
 (18)
(18)
2. Phase Error
Path length error for the lens is defined as the difference in path length between a central ray through the origin and any other ray [1], both of which is traced from an arbitrary point on the focal arc through the lens and terminates normal to the emitted wave front.
When a feed is placed at one of the focal point, corresponding emitted wave front has no phase error. When the feed is displaced from the focal point, the corresponding wave front will have a phase error. However, for wide angle scanning lens must be focused at all the intermediate points along the focal arc.
Let a feed be located at point R (Figure 1) on the focal arc for the out going beam at an angle –q. Let Ra and Rb be the phase shift from the feed position to the wave front when the ray is passing through P (X, Y) and O1, respectively. The phase error is given by
 (19)
(19)
where
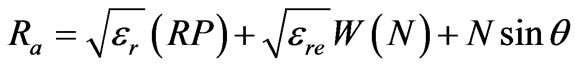 (20)
(20)
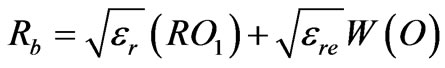 (21)
(21)
Let, (RO1) = H Coordinates of point R is given by (G-H cosq1 , H sinq1) where
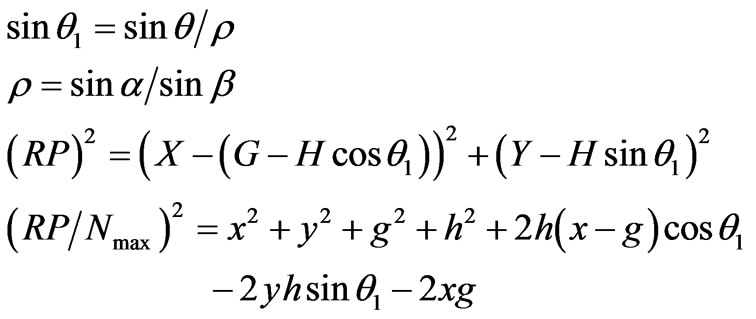
To calculate the value of H We use equation 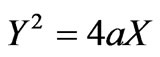 and Equation (18)
and Equation (18)
From Figure 1 for new point (G-H cosq1, H sinq1)
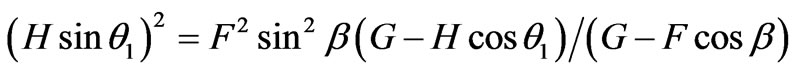 (22)
(22)
To calculate H

Normalizing w.r.t Nmax and calculating h
 (23)
(23)
Solving the above quadratic equation we get value of h and thus we get all the parameters to calculate path length error d L.
 (24)
(24)
3. Specific Design Example
This section describes an example of the design and analysis of rotman lens and parabolic refocusing lens to feed a linear array of waveguide horns. It is required to design the lens for the following requirements G = 3 λ: g = 1.8942 F = 2.7 λ: f = 1.705 Angular coverage = ± 35˚
Number of antenna elements = 10 Central frequency = 3.4641 GHz The complete structure is assumed to be fabricated in a micro strip substrate of thickness 1/16 inch and dielectric constant 3.7 and the loss tangent is 0.001.
4. Result and Discussion
Figure 2 shows the variation of the normalized phase

Figure 2. Variation of the normalized phase error ( ) with the normalized lens aperture for different value of scanning angels (q).
) with the normalized lens aperture for different value of scanning angels (q).
error (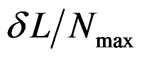 ) with the normalized lens aperture for different value of scanning angels (q). Figure 3 shows the variation of normalized phase error with “f” for different values of scanning angles. It may be noted that error is minimum at specific value of “f”. Figure 4 shows the variation of normalized phase error with “g” for different values of scanning angles and Figure 5 shows the Normalized phase error for the Rotman lens Vs the Normalized phase error parabolic refocusing lens. Table 1 shows the variation of normalized phase error “a” for different scanning angles. Phase error is 0 for a = q.
) with the normalized lens aperture for different value of scanning angels (q). Figure 3 shows the variation of normalized phase error with “f” for different values of scanning angles. It may be noted that error is minimum at specific value of “f”. Figure 4 shows the variation of normalized phase error with “g” for different values of scanning angles and Figure 5 shows the Normalized phase error for the Rotman lens Vs the Normalized phase error parabolic refocusing lens. Table 1 shows the variation of normalized phase error “a” for different scanning angles. Phase error is 0 for a = q.

Figure 3. Variation of normalized phase error with “f” for different values of scanning angles.

Figure 4. Variation of normalized phase error with “g” for different values of scanning angles.
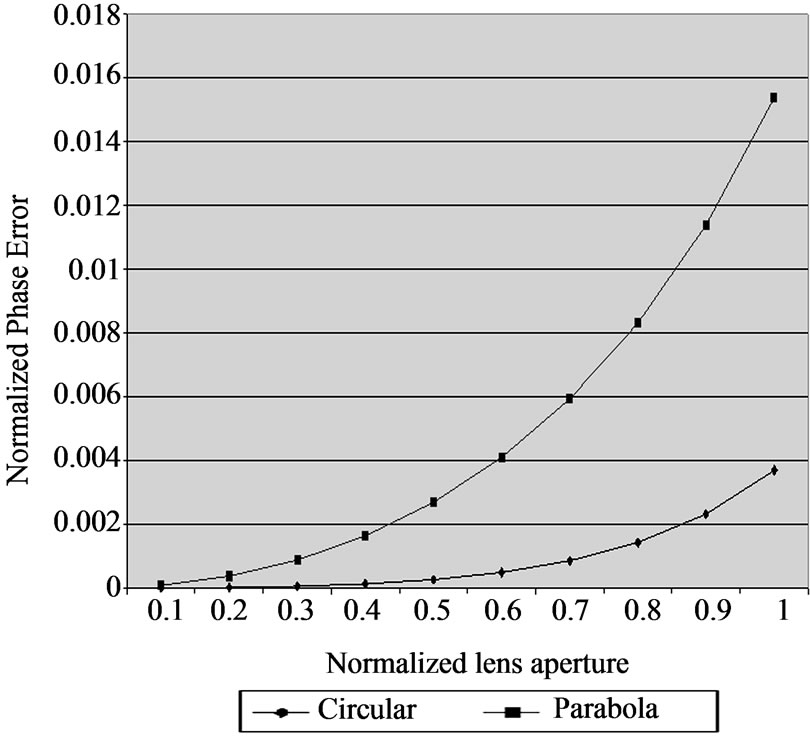
Figure 5. Normalized phase error for the rotman lens vs parabolic refocusing lens.
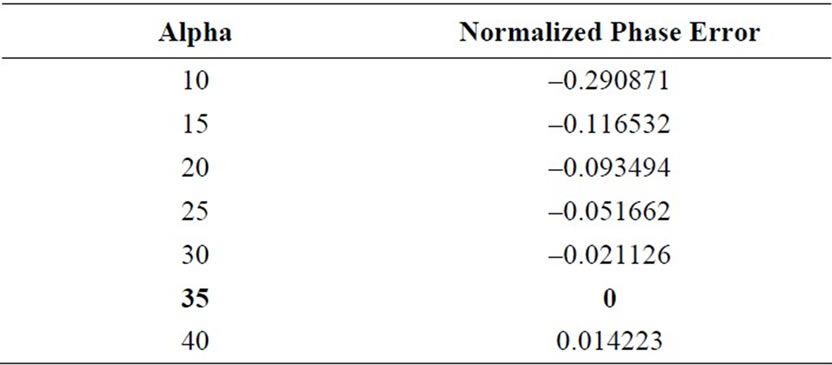
Table 1. Variation of normalized phase error “a” for different scanning angles, Phase error is 0 for a = q.
5. Concluding Remarks
Refocusing of Rotman type lens using parabolic focal arc has been performed. Phase error at the wave front has been calculated for the circular and parabolic focal arc lenses. Normalized phase error for the lenses has been compared. Normalized phase error for the parabolic refocusing lens is greater than the Rotman lens.
Path length error also depends upon α, as α approach towards scanning angle (θ), path length error decreases.
REFERENCES
- P. K. Singhal, P. C. Sharma and R. D. Gupta, “Recent Trends in Design and Analysis of Rotman-Type Lens for Multiple Beamforming,” International Journal of RF and Microwave Computer-Aided Engineering, Vol. 8, No. 4, 1998, pp. 321-338.
- P. K. Singhal, P. C. Sharma and R. D. Gupta, “Comparison of the Performance of the Rotman Type Lenses Obtained by Different Design Approaches,” TENCON 99. Proceedings of the IEEE Region 10 Conference, Cheju Island, Vol. 1, September 1999, pp. 738-741.

