Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 2 (2010) , Article ID: 1392 , 7 pages DOI:10.4236/jemaa.2010.22015
Low-loss, Broadband and Tunable Negative Refractive Index Metamaterial
![]()
1School of Communication and Information Engineering, University of Electronic Science and Technology of China, Chengdu, China; 2School of Opto-Electronic Information, University of Electronic Science and Technology of China, Chengdu, China.
Email: yongjunh@uestc.edu.cn, wgj@uestc.edu.cn, keguai2007@163.com
Received October 10th, 2009; revised November 22nd, 2009; accepted November 28th, 2009.
Keywords: Metamaterial, Negative Refractive Index, Tunability, Low-Loss, Broadband
ABSTRACT
This paper report on a low-loss, broadband, and tunable negative refractive index metamaterial (NRIM) consisting of yttrium iron garnet (YIG) slabs and printed circuit boards (PCBs). The YIG slabs under an applied magnetic field provide a negative permeability and the PCBs provide a negative permittivity. The substrates of the PCBs decuple the interactions between the YIG slabs and wire array deposed on such substrates. The effective electromagnetic parameters of the NRIM and the conditions of exhibiting the negative refractive index character are analyzed theoretically. Then the negative transmission and negative refraction characters are investigated numerically and experimentally. The results indicate that the NRIM exhibits negative pass band within the X-band with a bandwidth of about 1 GHz and a peak transmission power of about - 2.5 dB. While changing the applied magnetic field from 2300 Oe to 2700 Oe, the measured pass band of NRIM shift from 8.42 GHz to 9.50 GHz with a 2.7 MHz/Oe step. The results open a sample way to fabricate the NRIM, further, the metamaterial cloak and absorber.
1. Introduction
Since the negative refractive index metamaterial (NRIM) predicted by Veselago [1] was experimentally realized by Smith et al. [2] and verified by Shelby et al. [3] through negative refraction in a prism sample, much attention has been attracted on designing various NRIMs [4–9] and investigating applications [10,11]. Much of the fascination in NRIMs arises from their unusual electromagnetic properties such as the reversals of both Doppler shift and Cherenkov radiation [1], enhancement of evanescent wave [12], and subwavelength resolution imaging [13], etc. In the various NRIMs, most of them are realized by artificial metallic structures with metallic plasma resonance such as using wires to produce effective negative permittivity and using split-ring resonators (SRR) to provide effective negative permeability [2,14,15]. Recently, the investigations of electromagnetic cloak of invisibility based on the metallic plasma resonance structure metamaterial [16] have generated great interests [17]. However, most NRIMs proposed to date are based on immutable structure of the unit cell and result in a narrow band and not at all tunable.
In order to fabricate a broadband and tunable NRIM, the SRR structure resulting in the narrow band and untunability must be replaced by some other structures or materials. Some researchers proposed ferrimagnet based NRIM, that is, substitute ferrimagnet such as yttrium iron garnet (YIG) for the SRR structure to obtain the negative permeability [18–22]. Dewar gave the theoretical expressions of the effective parameters and analyzed the interaction of the ferrites and wires [18]. Cao et al. numerically investigated the electromagnetic wave propagation properties of the NRIM [19]. However such model cannot be fabricated easily in actually. Cai at al. proposed a simple way to fabricate the NRIM with ferrimagnet slabs and wire array [20]. Zhao et al. and He et al. fabricated the NRIM sample and investigated experimentally the negative transmission and tunability characters [21,22]. However, these authors mentioned above did not directly measure the refraction index character. They did not optimize the parameters so that the NRIM exhibits a low loss and reflection. And the most important thing is that they did not investigate the strategies for minimizing the loss when the NRIM is fabricated experimentally. Since the loss is a serious problem when the NRIM is used in engineering areas, we need to determine ways to reduce it, especially at high frequencies.
The aim of this work is to provide a low-loss, broadband, and tunable NRIM consisting of YIG slabs and printed circuit boards (PCBs). The YIG slabs under applied magnetic field give rise to a negative permeability and the PCBs provide a negative permittivity. This NRIM is designed because there are some advantages. For instance, it can be easily fabricated with YIG slabs and PCBs. The thickness of the wire depositing on PCBs has a very small value so that the frequency band in which the refraction index is negative can be achieved to far infrared and optical frequencies. And the interaction between YIG slabs and wires can be easily reduced by using the substrate layers.
In this paper we present the model of the NRIM and give the fabricated parameter values based on the theoretical analysis. Then we give the approximate theoretical results of the effective permeability and permittivity of the NRIM. The EM transmission properties are numerically investigated by using ANSOFT’s High Frequency Structure Simulator (HFSS) tools. In the end we experimentally investigate the negative transmission, tunability, and negative refraction properties by testing the NRIM sample in X-band rectangular waveguide.
2. Design and Fabrication
To design a low-loss, broadband, and tunable NRIM, the ferrimagnet is used to replace the SRR structures to provide the negative permeability. The PCBs are used to obtain the negative permittivity. The ferrimagnet has some particular properties. For instance, the loss in ferrimagnet is much smaller than typical conductor SRR [2], the effective permeability of ferrimagnet under the applied magnetic field is negative within a broad frequency band, and the frequency band of negative permeability can be dynamically and continuously tuned by changing the applied magnetic field. So the ferrimagnet is a desirable candidate to fabricate the tunable NRIM. However, the ferrimagnet under applied magnetic field would damage the negative permittivity of wire array. It can be reduced by using an insulating and nonmagnetic dielectric material [18] and the dielectric material must also be low-loss.
Consequently, based on the above analysis, the schematic of the NRIM is designed and presented in Figure 1. The structure parameters are also designed properly by numerical optimization. The yttrium iron garnet (YIG) slabs are used to give rise to negative permeability. Each slab has a dimension of 22.86 × 10.16 × 1 mm3, a saturation magnetization of 1830 Gs (1 Gs = 103/(4p) A/m), and a line width of about 22 Oe (1 Oe =103/(4p) A/m). The substrates of PCBs, which are made from RT/duriod 5880 glass microfiber reinforced PTFE composites, are used to reduce the interaction between YIG slabs and wire array. Each PCB has a dimension of 22.86 × 10.16 ×0.254 mm3. The wires depositing on the substrates have a dimension of 0.2 × 10.16 × 0.018 mm3 and periodic distance of 1.508 mm along the x axis. There are one layer PCB and one layer substrate in per two YIG slabs, as shown in Figure 1, so the NRIM is a two-dimension periodic structure in the x axis and z axis. The sizes of YIG slabs, substrates, and wires presented above are specially designed so that the wires dimension is much smaller than the periodic lattice space and the substrates dimension is near the geometric mean of wires dimension and periodic distance. The above parameter values are chosen because it can minimize the interaction of YIG slabs and wire arrays [18].
3. Theories
In this section we briefly show the theoretical analysis of the NRIM presented in Section 2. We mainly focus on the effective permeability and permittivity which describe the macroscopical characters of the composite NRIM. Dewar have analyzed the theoretical results of the effective permeability of the ferrimagnet under applied magnetic field and the effective permittivity of the wire array surrounded with a dielectric material in the ferrimagnetic host [18]. Although the NRIM mode presented here is not the same as mode presented in Ref. [18], the same formula can be used to analyze the mode presented in this paper because the thickness of PCBs is much smaller than YIG’s and the effective radius of wire is much smaller than the thickness of PCBs. So assuming a transverse electromagnetic (TEM) wave propagates along the x(-z) axis with the electric field along the y axis and the magnetic field along the z(x) axis and assuming a applied magnetic field parallel to the wires (the y axis), the effective permeability and permittivity of the NRIM presented here can be given by [18]
 (1)
(1)

Figure 1. The schematic of NRIM consisting of ferrites and PCBs
 (2)
(2)
 (3)
(3)
Here Ms is saturation magnetization of YIG. γ is gyromagnetic ratio. Λ is a phenomenological damping parameter describing loss intrinsic to the magnetic material [18]. H0 is the applied magnetic field. εf is the permittivity of ferrite. σeff is the effective conductivity of wire arrays. ε0 is the permeability of air. ω is the angular frequency. r1 is the radius of the wire. r2 is the radius of the insulated layer. And a is the periodic lattice constant. Using the equations presented above and parameter values presented in Section 2, the effective permeability and permittivity are calculated and shown in Figure 2.


Figure 2. (a) The calculated effective permeability and permittivity by using the Equations (1)-(3). The other parameters are Λ = 107, H0 = 2300 Oe. (b) The calculated effective permeability under different applied magnetic fields
It can be found from Figure 2(a) that both the effective permeability μeff and permittivity εeff exhibit typical resonant character. In the broad range from 9.18 GHz to 11.5 GHz both the real part of μeff and εeff are negative, so the EM wave can be propagated in such medium. Moreover the bandwidth can be expanded further by choosing different YIG slabs and designing dimensions of the wire array. The image parts of the two parameters, which show the loss in the medium, are much smaller and approximately equal to 0. Moreover, as shown in Figure 2(b), the resonant frequencies of μeff increase from 8.66 to 9.85 GHz as H0 rises from 2300 to 2700 Oe. So the NRIM presented in this paper can be tuned by changing the applied magnetic field.
4. Results
In this section, we first investigate numerically the EM properties of the designed NRIM shown in Figure 1 by using ANSOFT’s High Frequency Structure Simulator (HFSS) tools, and then measure experimentally the transmission properties and refraction character.
4.1 Simulated Results
To numerically simulate the transmission properties of the NRIM under the incidence of TEM waves, we use a planar waveguide system with a cross section of 22.86 × 10.16 mm2. The NRIM is put at the middle of planer waveguide with the perfect E boundaries at up and down sides and the Master and Slave boundaries at the left and right sides. Here we simulate two cases.
Case (1): An EM wave propagated along the z axis with an electric field along the y axis and magnetic field along the -x axis, and a dc applied magnetic field along the y axis. The parameter values used to simulation are the same as Section 3. The simulated magnitudes of S11 and S21 of the NRIM under the applied magnetic field of 2300 Oe are shown in Figure 3(a) (black line).
Case (2): The EM wave propagated along the x axis with the electric field along the y axis and the magnetic field along the z axis, and the dc applied magnetic field along the y axis. The parameters values are the same as Section 3 too. The simulated magnitudes of the S11 and S21 of the NRIM under the applied magnetic field of 2300 Oe are shown in Figure 3(a) (light grey line).
At the same time, the magnitudes of the S21 of the NRIM in case (2) under a series of values of the applied magnetic fields are simulated and are shown in Figure 3(b). In case (1), the propagation direction of the EM wave is perpendicular to the YIG slabs, while in case (2), the propagation of the EM waves is parallel to the YIG slabs.
In case (1), as shown in Figure 3(a) (black lines), the NRIM under the applied magnetic field of 2300 Oe exhibits a transmission pass band in which the center frequency is about 10.2 GHz, the peak transmission power

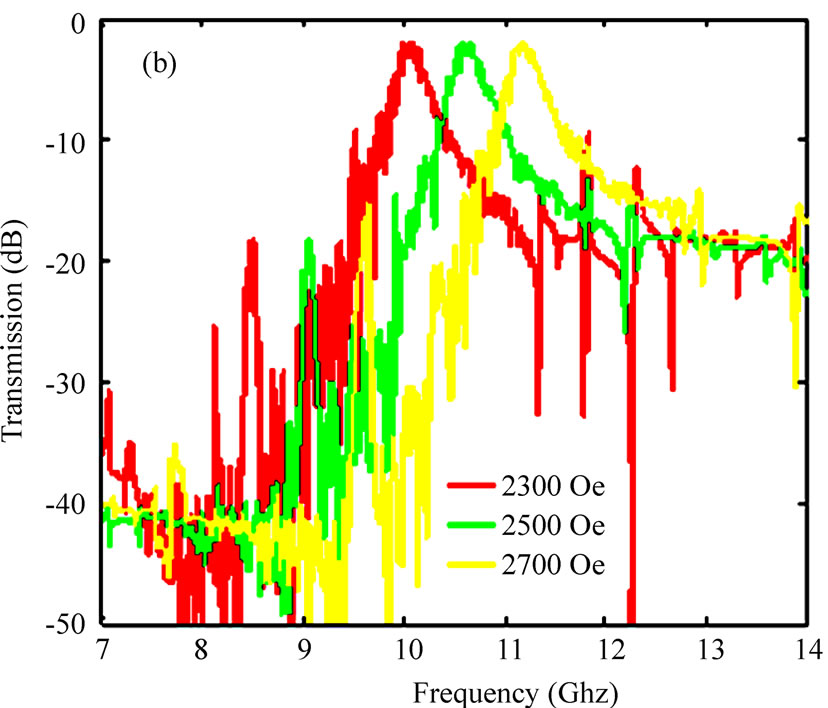
Figure 3. (a) The numerically simulated results of the NRIM in Case (1) (red lines) and Case (2) (green lines). The magnitudes of S11 and S21 of the NRIM under the applied magnetic field of 2300 Oe are presented. (b) The magnitudes of the S21 of the NRIM under a series of values of the applied magnetic field in Case (2)
is about -8 dB, and the bandwidth is about 1 GHz. The green lines in Figure 3(a) show the transmission character corresponding to the Case (2). There is a pass band at 10 GHz with a transmission power of -2.5 dB and a bandwidth of 1 GHz. From the two cases we can know that the NRIM presented in this paper exhibits obviously a pass band with a very low loss and broad frequency band. Moreover, the loss and reflection in case (2) are smaller than in case (1). We can also know from Figure 3(a) that there is another transmission pass band at 8.4 GHz. The unexpected pass band can be explained as follows. As shown in Figure 2(a), both the permeability and permittivity are positive at the range of 8.42 GHz – 8.63 GHz. So the composite medium can transfer EM waves too in such range with a positive character. This is due to the interaction between the YIG slabs and wires. Figure 3(b) shows the tunability of the NRIM under different applied magnetic fields in case (2). The peak of transmission shift from 10 GHz to 11.2 GHz while changing the applied field from 2300 Oe to 2700 Oe.
The simulated results show that the loss of the composite presented here is much smaller than other NRIMs [2,4–9]. The loss of NRIM is generally come from ohmic loss of wires and dielectric loss of substrates. Replacement of the cut-ring structures [2] with ferrites can reduce the loss since ferrites can be less lossy than typical conductors. Choosing bigger wires or superconductors and low-loss substrates can further reduce the loss. The transmission bandwidth of NRIM is determined by the forbidden bandwidth of YIG, namely the ferromagnetic resonance (FMR) and ferromagnetic antiresonance (FMAR) frequencies [18]. It is well known that the FMR frequency and FMAR frequency are given by [18]
 (4)
(4)
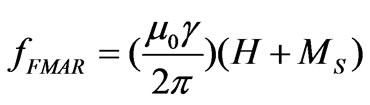 (5)
(5)
So the bandwidth can be expanded and the center frequency can be improved by choosing the YIG slabs of bigger saturation magnetization. From Equations (1)–(3) we can also know that the tunability of the NRIM is dependent on the tunability of negative permeability in the YIG slabs. The wire array has a negative permittivity within a wide frequency region below the plasma frequency [14]. So the region of negative index of the NRIM can be tuned from the low frequency to the plasma frequency of wire array.
4.2 Experimental Results
In order to confirm experimentally the conclusions presented in Section 3 and the numerical results presented above, we fabricated the NRIM sample to measure experimentally the transmission character and also fabricated the prism-shaped prototype to determine the refractive index via the Snell’s law.
In practice, the NRIM sample consisting of YIG slabs and PCBs is shown in Figure 4(a). The fabricated sizes are the same as Section 2. We experimentally investigate the transmission character of the NRIM by measuring the scattering parameters. The NRIM sample was put at the middle of X-band waveguide, the waveguide was connected to a vector network analyzer Agilent N5230A (40 MHz–40 GHz). An EM wave propagated along the x axis with an electric field along the z axis and magnetic field along the y axis. An electromagnet was used to generate the external magnetic field along the z axis. The transmission coefficient S21 of the NRIM sample and the YIG slabs under the applied magnetic field of 2500 Oe and PCBs were measured using the network analyzer at X-band, were shown in Figure 4(b). To demonstrate the tunability of the NRIM we also have carried out measurements of transmission coefficient in different applied magnetic fields, and the results were shown in Figure 4(c).

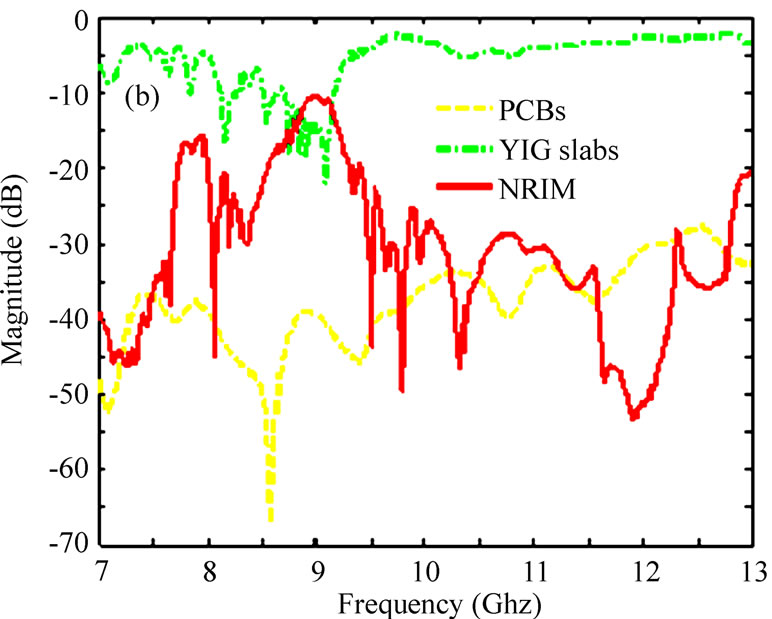

Figure 4. (a) The fabricated NRIM sample. The fabricated sizes are the same as Section 2. (b) The measured transmission results of the NRIM under the applied magnetic field of 2500 Oe in the X-band waveguide. (c) The magnitudes of the S21 of the NRIM under a series of values of the applied magnetic field


Figure 5. (a) The fabricated prism-shaped NRIM sample and the refraction measured system. (b) The measured refractive angle of the NRIM sample under the applied magnetic field of 2300 Oe and paraffin sample in the same condition
It can be seen from Figure 4(b) that there is a pass band within the forbidden band of both the YIG slabs and PCBs under the field of 2500 Oe. The peak transmission power is about -10.5 dB at 9 GHz and the bandwidth is about 1 GHz. These experimental results are confirming the simulated results indicated in subsection 4.1 very well. But the measured transmission frequency band of NRIM sample is lower than the simulated frequency band. This is because that the experimental measured condition cannot achieve the ideal simulated condition and the applied magnetic field is not completely act on YIG slabs. The measured tunability [Figure 4(c)] of NRIM sample under different fields indicate that, while changing the field from 2300 Oe to 2700 Oe, the magnitude of S21 shifted from 8.42 GHz to 9.50 GHz with the sensitively tuning rate of 2.7 MHz/Oe.
For the refraction experiment, we fabricated a prismshaped NRIM sample inserted in Figure 5(a) and a refraction measured system [3] shown in Figure 5(a). The sample was placed between the two circular copper plates. The top plate had a pivot in the center, about which an attached X-band microwave waveguide could be rotated to measure transmitted power at arbitrary refraction angles. A beam of incidence microwaves whose electric field was polarized such that it was uniform and parallel to the wires propagated through the sample and encountered the second surface of the prism, the refraction interface, and was refracted into a direction. To measure the exit angle, we rotated the waveguide assembly in 2° steps and recorded the transmitted power spectrum over the entire X-band range at each step, using an Agilent N5230A vector network analyzer. The normal to the NRIM refraction surface was at an angle of 18.43° with respect to the normal of the incident surface. Experiments were performed with a prism-shaped NRIM sample under the field of 2300 Oe as well as with a similarly shaped paraffin sample as a control.
As can be seen in Figure 5(b), at 8.3 GHz, the microwaves were refracted to negative angles of the normal for the NRIM sample. The positive refraction of paraffin sample was shown in Figure 5(b) too. The paraffin data show refraction as would be predicted for nParaffin = 1.5 ± 0.1, whereas for the NRIM, the measured exit angle of θ = -32° implies that nNRIM = -1.6 ± 0.1.
5. Conclusions
In conclusion, a low-loss, broadband, and tunable negative refractive index metamaterial consisting of YIG slabs and PCBs is designed and fabricated. Both the simulated and experimental properties of NRIM are investigated. The simulated scattering parameters of the NRIM indicate that there is a pass band in the X-band and the bandwidth is about 1 GHz and the pass band can be shifted by changing the magnetic field. Besides, the experimentally measured scattering parameters show that there is a pass band within the forbidden band of both the YIG slabs and PCBs. The magnitude of S21 shifted from 8.42 GHz to 9.50 GHz with the sensitively tuning rate of 2.7 MHz/Oe when changing the applied magnetic field from 2300 Oe to 2700 Oe. Both the simulated results and the experimentally measured results verify the correctness of the designed NRIM. The results open a sample way to fabricate NRIM, further, the metamaterial cloak and absorber.
6. Acknowledgments
This work was supported by the National Science Foundation of China under Grant Nos. 60571024, 60771046, and 60588502.
REFERENCES
- V. G. Veselago, “The electrodynamics of substances with simultaneously negative values of permittivity and permeability,” Soviet Physics Uspekhi, Vol. 10, pp. 509–514, 1968.
- D. R. Smith, W. J. Padilla, and D. C. Vier, “Composite medium with simultaneously negative permeability and permittivity,” Physics Review Letters, Vol. 84, pp. 4184–4187, 2000.
- R. A. Shelby, D. R. Smith, and S. Schultz, “Experimental verification of a negative index of refraction,” Science, Vol. 292, pp. 77–79, 2001.
- R. W. Ziolkowski, “Design, fabrication, and testing of double negative metamaterials,” IEEE Transaction on Antennas and Propagation, Vol. 57, pp. 1516–1528, 2003.
- H. Chen, L. Ran, J. Huangfu, X. Zhang, K. Chen, T. M. Grzegorczyk, and J. A. Kong, “Left-handed materials composed of only S-shaped resonators,” Physics Review E, Vol. 70, 057605-1-4, 2004.
- G. V. Eleftheriades, A. K. Iyer, and P. C. Kremer, “Planar negative refractive index media using periodically L-C loaded transmission lines,” IEEE Transaction on Microwave Theory and Techniques, Vol. 50, pp. 2702–2712, 2002.
- L. Liu, C. Caloz, C. Chang, and T. Itoh, “Forward coupling phenomena between artificial left-handed transmission lines,” Journal of Applied Physics, Vol. 92, pp. 5560–5565, 2002.
- M. Notomi, “Theory of light propagation in strongly modulated photonic crystals: Refractionlike behavior in the vicinity of the photonic band gap,” Physical Review B, Vol. 62, pp. 10696–10705, 2000.
- P. V. Parimi, W. T. Lu, J. S. Derov, J. Sokoloff, J. S. Derov, and S. Sridhar, “Negative refraction and lefthanded electromagnetism in microwave photonic crystals,” Physics Review Letters, Vol. 92, 127401-1-4, 2004.
- S. Lim, C. Caloz, and T. Ttoh, “Electronically scanned composite right/left handed microstrip leaky-wave antenna,” IEEE Microwave Wireless Components Letters, Vol. 14, pp. 277–279, 2004.
- H. Tao, N. I. Landy, C. M. Bingham, X. Zhang, R. D. Averitt, and W. J. Padilla, “A metamateial absorber for the terahertz regime: Design, fabrication and characterization,” Optics Express, Vol. 16, pp. 7181–7188, 2008.
- D. Qiang and G. Chen, “Enhancement of evanescent waves in waveguides using metamaterials of negative permittivity and permeability,” Applied Physics Letters, Vol. 84, pp. 669–671, 2004.
- K. Aydin and E. Ozbay, “Left-handed metamaterial based superlens for subwavelength imaging of electromagnetic waves,” Applied Physics A, Vol. 87, pp. 137–141, 2007.
- J. B. Pendry, A. J. Holden, W. J. Stewart, and I. Youngs, “Extremely low frequency plasmons in metallic mesostructures,” Physics Review Letters, Vol. 76, pp. 4773–4776, 1996.
- J. B. Pendry, A. J. Holden, D. J. Robbins, and W. J. Stewart, “Magnetism from conductors and enhanced nonlinear phenomena,” IEEE Transaction on Microwave Theory and Techniques, Vol. 47, pp. 2075–2084, 1999.
- D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr, and D. R. Smith, “Metamaterial electromagnetic cloak at microwave frequencies,” Science, Vol. 314, pp. 977–980, 2006.
- H. Chen, Z. Liang, P. Yao, X. Jiang, H. Ma, and C. Chan, “Extending the bandwidth of electromagnetic cloaks,” Physics Review B, Vol. 76, 201104-1-4, 2007.
- G. Dewar, “The applicability of ferromagnetic hosts to nanostructures negative index of refractive (left-handed) materials,” Proceedings SPIE, Vol. 4806, pp. 156–166, 2002.
- Y. J. Cao, G. J. Wen, K. M. Wu, and X. H. Xu, “A novel approach to design microwave medium of negative refractive index and simulation verification,” Chinese Science Bulletin, Vol. 52, pp. 433–439, 2007.
- X. B. Cai, X. M. Zhou, and G. K. Hu, “Numerical Study on Left-Handed Materials Made of Ferrite and Metallic Wires,” Chinese Physics Letters, Vol. 23, pp. 348–351, 2006.
- H. J. Zhao, J. Zhou, Q. Zhao, B. Li, L. Kang, and Y. Bai, “Magnetotunable left-handed material consisting of yttrium iron garnet slab and metallic wires,” Applied. Physics Letters, Vol. 91, 131107-1-3, 2007.
- Y. X. He, P. He, S. D. Yoon, P. V. Parimi, F. J. Rachford, V. G. Harris, and C. Vittoria, “Tunable negative index metamaterial using yttrium iron garnet,” Journal of Magnetism and Magnetic Materials, Vol. 313, pp. 187–191, 2007.

