Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 2 (2012) , Article ID: 17619 , 10 pages DOI:10.4236/ijcns.2012.52015
Optimal Allocation of Radio Resource in Cellular LTE Downlink Based on Truncated Dynamic Programming under Uncertainty
Department of Systems Engineering, Faculty of Engineering Complex, University of Lagos, Lagos, Nigeria
Email: yomi_ajofoyinbo@yahoo.co.uk, aajofoyinbo@unilag.edu.ng, olukeh@yahoo.com
Received December 2, 2011; revised January 19, 2012; accepted February 3, 2012
Keywords: Optimal Allocation; Resource Block; Truncated; Dynamic Programming; Uncertainty
ABSTRACT
In the Cellular Long-Term Evolution (LTE) downlink, the smallest radio resource unit a Scheduler can assign to a user is a Resource Block (RB). Each RB consists of twelve (12) adjacent Orthogonal Frequency Division Multiplexing (OFDM) sub-carriers with inter-subcarrier spacing of 15 kHz. Over the years, researchers have investigated the problem of radio resource allocation in cellular LTE downlink and have made useful contributions. In an earlier paper for example, we proposed a deterministic dynamic programming based technique for optimal allocation of RBs in the downlink of multiuser Cellular LTE System. We found that this proposed methodology optimally allocates RBs to users at every transmission instant, but the computational time associated with the allocation policy was high. In the current work, we propose a truncated dynamic programming based technique for efficient and optimal allocation of radio resource. This paper also addresses uncertainty emanating from users’ mobility within a Cell coverage area. The objective is to significantly reduce the computational time and dynamically select applicable modulation scheme (i.e., QPSK, 16QAM, or 64QAM) in response to users’ mobility. We compare the proposed scheme with the Fair allocation and the earlier proposed dynamic programming based techniques. It is shown that the proposed methodology is more efficient in allocating radio resource and has better performance than both the Fair Allocation and the deterministic dynamic programming based techniques.
1. Introduction
In the 3rd Generation Partnership Project (3GPP) LongTerm Evolution (LTE), Orthogonal Frequency Division Multiplexing (OFDM) is chosen as the radio transmission scheme. Packet scheduling is one of the LTE Radio Resource Management (RRM) functions, which is responsible for allocating resources to users. In taking scheduling decisions, RRM takes into account the Channel Quality Information (CQI) from the User Equipment (UE), the Quality of Service (QoS) requirements and the buffer status. The downlink of LTE Cellular System is based on Orthogonal Frequency Division Multiple Access (OFDMA), which provides efficient multi-user access and intra-cell interference avoidance. The smallest radio resource unit that the scheduler can assign to a user is a Resource Block (RB) [1]. In the downlink of LTE Cellular System, radio resources are partitioned in both the frequency and time domains. Access to radio resource is controlled in terms of frames and frequency channels. These frames and frequency channels are referred to as the OFDM Resource Blocks (RBs). Each RB consists of 12 adjacent OFDM sub-carriers with intersubcarrier spacing of 15 kHz. Each sub-frame (i.e., 1 ms in the time domain) consisting of two (2) RBs is divided into fourteen (14) symbols of which up to three symbols at the start of the sub-frame can be used for controlling channel signalling. The allocation of RBs to user is done by the scheduler and scheduling decision is taken during each Transmission Time Interval (TTI) of 1 ms for each sub-frame. The allocated RBs and the selected modulation and coding schemes are signalled to the scheduled user on the Physical Downlink Control Channel (PDCCH) (Iosif and Banica [2]). The dynamic scheduler also interact with the Hybrid Automatic Repeat Request (HARQ) manager as it is responsible for scheduling retransmissions and it may also take into account the QoS attributes and buffer information (Holma and Toskala [3]). In recent years, researchers have investigated problem of radio resource allocation in LTE Downlink and have made useful contributions. Huang et al. [4] investigated the problem of gradient-based scheduling and resource allocation for the downlink of a Cellular OFDM system, which reduces to solving a convex optimisation problem in each time slot. The work considered scheduling and resource allocation for the downlink of a Cellular OFDM system, with various practical considerations including integer tone allocations, different sub-channelization schemes, maximum signal-to-noise ratio constraint per tone, and “self-noise” due to channel estimation errors and phase noise. The authors proposed an algorithm that automatically yields an integer carrier allocation. Kasier and Ahmed [5] proposed a priority based resource allocation algorithm for heterogeneous services in the relay enhanced Orthogonal Frequency Division Multiple Access (OFDMA) downlink systems. The aim of the research was to maximise the system throughput while satisfying the Quality of Service (QoS) of the heterogeneous services comprising Real Time (RT) and NonReal-Time (NRT) services. The proposed algorithm reduces the outage probability of the system and increases the system throughput. Anding et al. [6] presented an adaptive sub-carrier and power allocation scheme for OFDMA systems according to their different QoS requirement(s) and traffic type. The proposed algorithm maximised the transmission data rate while satisfying total power constraint and a certain Bit Error Rate (BER) requirement. This algorithm first allocates sub-carriers and bits to high priority users according to their rates and Bit Error Rate (BER) requirement, and then distributes the residual resources to the ordinary users in terms of the proportional fairness principle. Simulation results show that the proposed method has better performance than the existing algorithms. In [7], Kumar et al. proposed new heuristic algorithms to solve the sub-carrier, bit, and power allocation in polynomial computational complexity. The two-stage allocation algorithms include the initial sub-carrier assignment and the iterative improvement two-steps. Simulation results show that the performance of the proposed heuristic algorithm is close to that of the optimum solution. Li and Liu [8] proposed a two-level resource allocation scheme, where the first level coordinates Cells while the second level performs per-Cell optimisation. Moreover, Koutsopoulos and Tassiulas [9] presented two classes of centralised heuristic algorithms. The first one considers each sub-carrier in each Cell. The results obtained show that the first class of heuristics performs better and quantify the input of different parameters on system performance. Thonabalasingham et al. [10] worked on joint allocation of various radio resources and concluded that joint allocation of various radio resources has a clear potential over methodologies that allocate single resource. In [11], Koutsimanis and Fodor worked on the elastic nature of data applications. In this work, each user is associated with a minimum and maximum Resource Block requirements and the resource allocation problem consists of maximising the overall throughput such that these requirements are met. Wong and Evans [12] developed optimal resource allocation algorithms for OFDMA systems assuming the availability of only partial (imperfect) Channel State Information (CSI). The authors considered both continuous and discrete weighted sum rate maximisation subject to total power constraints, and average bit error rate constraints for the discrete rate case. The work of Hosein [13] focused on the optimal allocation of power and bandwidth with the objective of maximising the sector-wide throughput. The work determined the regions within which 1) a frequency reuse factor of unity is optimal; 2) orthogonal frequency allocation is optimal; and 3) joint processing of signals from both sectors is optimal. Zhou et al. [14] proposed a Genetic Algorithm (GA) based cross-layer resource allocation for the downlink multiuser wireless OFDM system with heterogeneous traffic. The GA was used to maximise the sum of weighted capacities of multiple traffic queues at the Physical layer, where the weights are determined by the Medium Access Control (MAC) layer. In [15], Ergen et al. proposed a fair scheduling scheme that allocates sub-carriers to users and then determine the number of bits transmitted on each subcarrier. In an earlier paper, Ajofoyinbo and Orolu [16] proposed a dynamic programming based technique for optimal allocation of radio resource in the downlink of multi-user LTE Cellular System. The main contribution of this work is optimal allocation of RBs to users. Indeed, this optimal allocation of RBs yields maximum cumulative contribution to the overall network throughput at every transmission instant, but the associated computational time is normally high. In the current work, a truncated dynamic programming based technique is proposed for efficient and optimal allocation of radio resource in the downlink of a multi-user LTE Cellular System. The methodology also addresses uncertainty emanating from users’ mobility within a Cell coverage area.
The proposed technique maximises instantaneous channel throughput by efficiently and optimally allocating RBs to users, using less computational time.
The remainder of the paper is organized as follows. Problem formulation is presented in Section 2. This includes systems modelling and allocation policy. The problem solution and simulation of the proposed model is presented in Section 3. This is followed by a discussion of simulation results in Section 4. Section 5 concludes the paper.
This paper contributes to knowledge in the field of optimal allocation of RBs to achieve maximum instantaneous throughput in the downlink of multi-user LTE Cellular System.
2. Problem Formulation
In this section, we present the systems modelling and allocation policy for the proposed Truncated Dynamic Programming (TDP) based technique.
2.1. Systems Modelling for the TDP Technique
The proposed TDP under uncertainty model consists of fifty-one (51) states, namely: 0, 2, 4, …, 98, 100. These states represent the number of allocated RBs. The RBs are allocated in multiples of 2 RBs, starting with zero RB. We note that in the earlier proposed deterministic dynamic programming based technique; the system consisted of six (6) states. Moreover, the proposed model consists of n stages, which represent the scheduled users on the LTE downlink. In developing the recursive optimisation procedure, we obtain a solution of the overall nstage problem by first solving a one-stage problem, and by sequentially including one stage at a time, solving one-stage problems until the overall optimum is reached. The applicable dynamic programming procedure is the Back Induction (BI) process wherein the first stage to be analysed is the final stage of the problem and the n-stage problem is solved moving backwards one stage at a time until all stages are included to obtain optimal solution (Hillier and Lieberman [17]). We define the following variables:
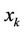 = Possible allocation of RBs
= Possible allocation of RBs
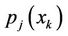 = Throughput obtainable from possible allocation of
= Throughput obtainable from possible allocation of  RBs to user j.
RBs to user j.
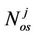 = Number of OFDM symbols for user j.
= Number of OFDM symbols for user j.
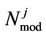 = Number of bits per OFDM Symbol for user j.
= Number of bits per OFDM Symbol for user j.
 = Number of Resource Elements (RE).
= Number of Resource Elements (RE).
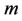 = Total number of RBs.
= Total number of RBs.
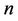 = Total number of users.
= Total number of users.
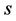 = Number of RBs still available for allocation.
= Number of RBs still available for allocation.
The objective is to choose 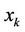 so as to Maximize
so as to Maximize 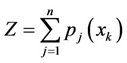 (1)
(1)
Subject to 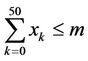 (2)
(2)
where
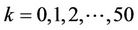 (3)
(3)
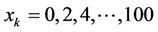 (4)
(4)
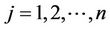 (5)
(5)
We note that
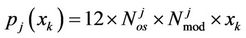 (6)
(6)
and
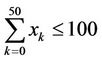 (7)
(7)
2.2. Allocation Policy and Recursion for the Proposed Truncated Dynamic Programming (TDP) Technique
We note that the truncated dynamic programming analysis starts from the last user (i.e., j = n, the final stage of the problem), but actual allocation of RBs starts with the first user (i.e., j = 1).
In this proposed model, the computations leading to the allocation of RBs follow a recursive procedure. We define 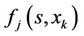 as the cumulative contribution of user
as the cumulative contribution of user 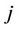 to the objective function, given
to the objective function, given 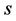 available RBs and
available RBs and 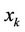 allocated RBs to user
allocated RBs to user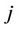 .
.
For the last user (i.e.,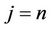 ),
),
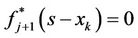 (8)
(8)
Thus,
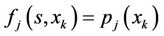 (9)
(9)
From the last-but-one-user (i.e., j = n – 1) to the first user (i.e., j = 1), we apply Equation (10).
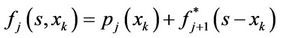 (10)
(10)
2.3. Motivation for Truncating the Dynamic Programming (DP) Procedure
The motivation for truncating the dynamic programming procedure is the determination of the point, beyond which it is no longer efficient to allocate RBs to a particular user given available RBs. To achieve this, we compare current computed cumulative throughput with the last two consecutive preceding cumulative throughputs. If the current cumulative throughput is less than or equal to the last two consecutive preceding cumulative throughputs, then the procedure is terminated (or truncated). The decision is to choose the maximum cumulative contribution to total channel throughput among computed cumulative contributions (or throughputs).
In computing throughput of individual user given available RBs, we invoke Equation (10) and execute the following truncated dynamic programming procedure. In the course of executing this procedure, the truncation conditions are checked before every computation of cumulative contribution (or throughput).
Computation of Cumulative Throughput and Truncation Procedure
For j = 19, 18, …, 1 BEGIN For k = 0, 1, 2, …, 50 BEGIN
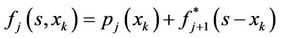 (11)
(11)
IF 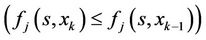 and
and 
THEN Truncate ELSE Compute cumulative throughput for next xk
END END The optimal allocation decision for user j, in relation to s and xk, is the maximum of the cumulative contributions to the total throughput. This is given by:
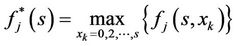 (12)
(12)
Thus, the corresponding allocated RBs is given by:
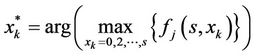 (13)
(13)
2.4. Effect of Truncation on Recursion
Without truncation, the back induction dynamic programming process computes cumulative contributions for all possible allocation of RBs (i.e.,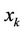 ), given available RBs (i.e., s). The Scheduler takes decision on optimal allocation of RBs at the end of all computations. With the truncation procedure however, the recursion is terminated when the truncation conditions are met; thereby reducing computational time and usage of other computational resources. Thus, in terms of contribution to the total network throughput, the truncation exercise enables the Scheduler to determine the point beyond which it is no longer efficient to allocate RBs to users much earlier than without truncation. The advantage to the network is that the time and other resources that would have been committed to computations beyond the truncation point are saved. In LTE, new scheduling decisions are taken in every Transmission Time Interval (TTI), which is 1 ms. The reduced computational time and timely decision on allocation of RBs would have positive effects on time of scheduling decisions.
), given available RBs (i.e., s). The Scheduler takes decision on optimal allocation of RBs at the end of all computations. With the truncation procedure however, the recursion is terminated when the truncation conditions are met; thereby reducing computational time and usage of other computational resources. Thus, in terms of contribution to the total network throughput, the truncation exercise enables the Scheduler to determine the point beyond which it is no longer efficient to allocate RBs to users much earlier than without truncation. The advantage to the network is that the time and other resources that would have been committed to computations beyond the truncation point are saved. In LTE, new scheduling decisions are taken in every Transmission Time Interval (TTI), which is 1 ms. The reduced computational time and timely decision on allocation of RBs would have positive effects on time of scheduling decisions.
3. Problem Solution and Simulation Results
The simulation and users’ transmission parameters are presented in Tables 1 and 2 respectively. At every scheduling instant, three modulation schemes are available to every user, namely: QPSK, 16QAM and 64QAM. The applicable modulation scheme depends on user’s location within a Cell coverage area. Uncertainty regarding user’s location is encapsulated in the truncated dynamic programming model at this stage. For example, a user with good signal strength may start transmission using 64QAM, and subsequently change at later transmission instant(s) to QPSK (or 16QAM) modulation scheme in response to change in location. The proposed truncated dynamic programming based technique was simulated on a Personal Computer using MATLAB Ver 7.10.0.449 (R2010a). Simulation results based on the proposed truncated and the existing dynamic programming techniques are obtained for the 20 network users. We are however constrained by limited space in this paper to present results for only the 18th user (i.e., j = 18) to demonstrate the efficiency and effectiveness of the proposed technique.
In the current paper, Option 1 represents data in Row 1 (i.e., from columns 3 to 6) for all users in Table 2. Similarly, Options 2 and 3 represent data in Rows 2 and 3 respectively (i.e., from Columns 3 to 6) for all users in Table 2. The management of uncertainty regarding dynamic selection of a modulation scheme shows the robustness of the proposed technique.
3.1. System Flowchart
The system flowchart for the implementation of the proposed technique is presented in Figure 1.
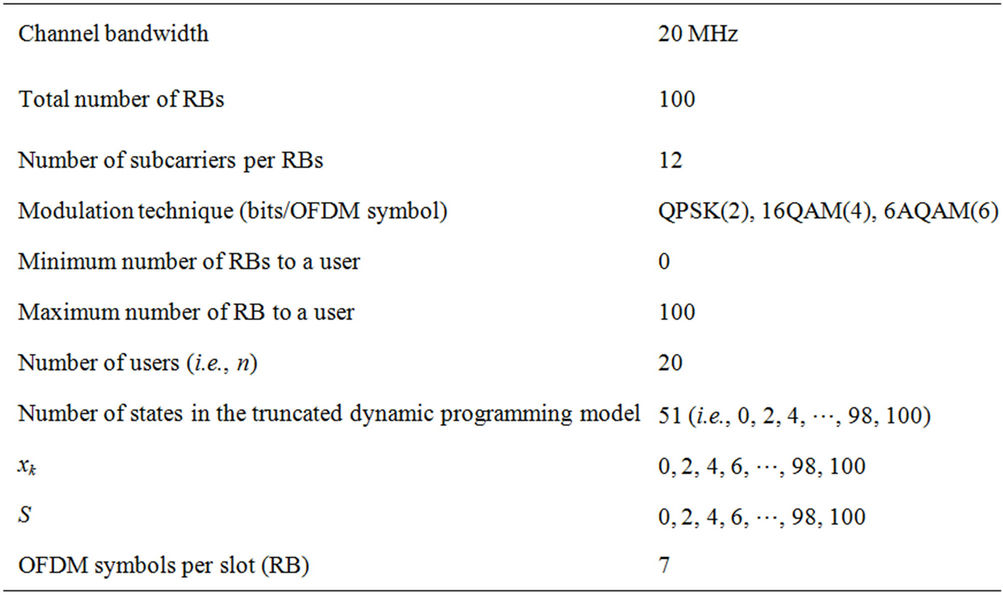
Table 1. Simulation parameters.
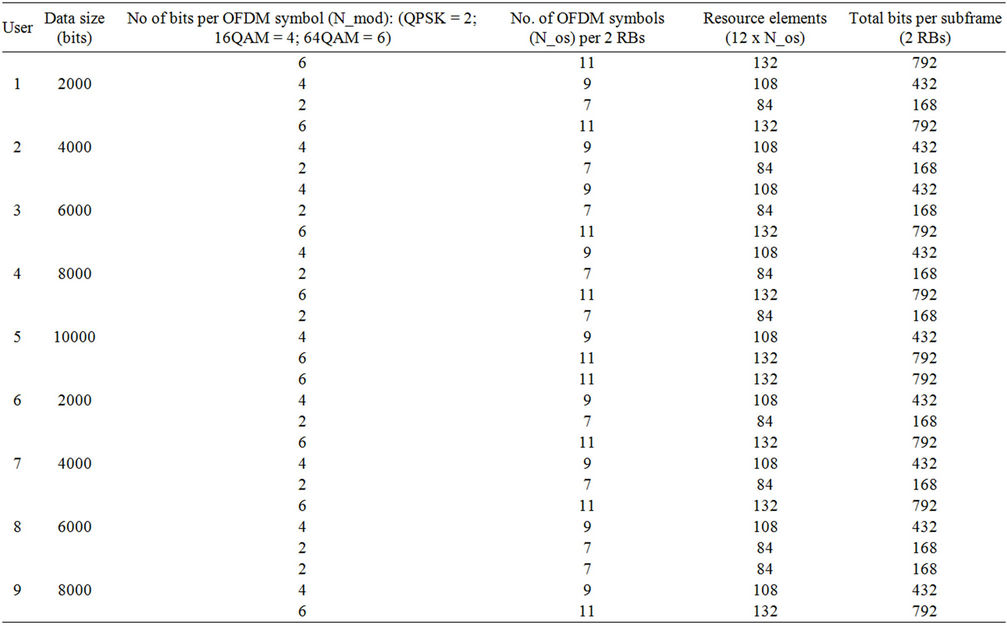
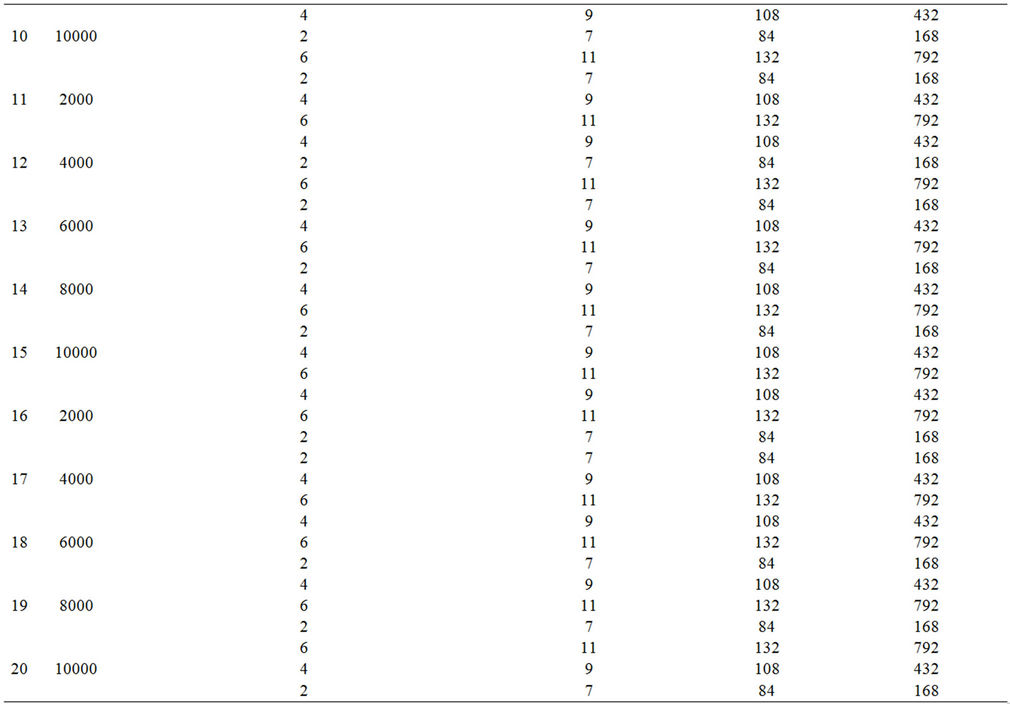
Table 2. Users’ transmission parameters.
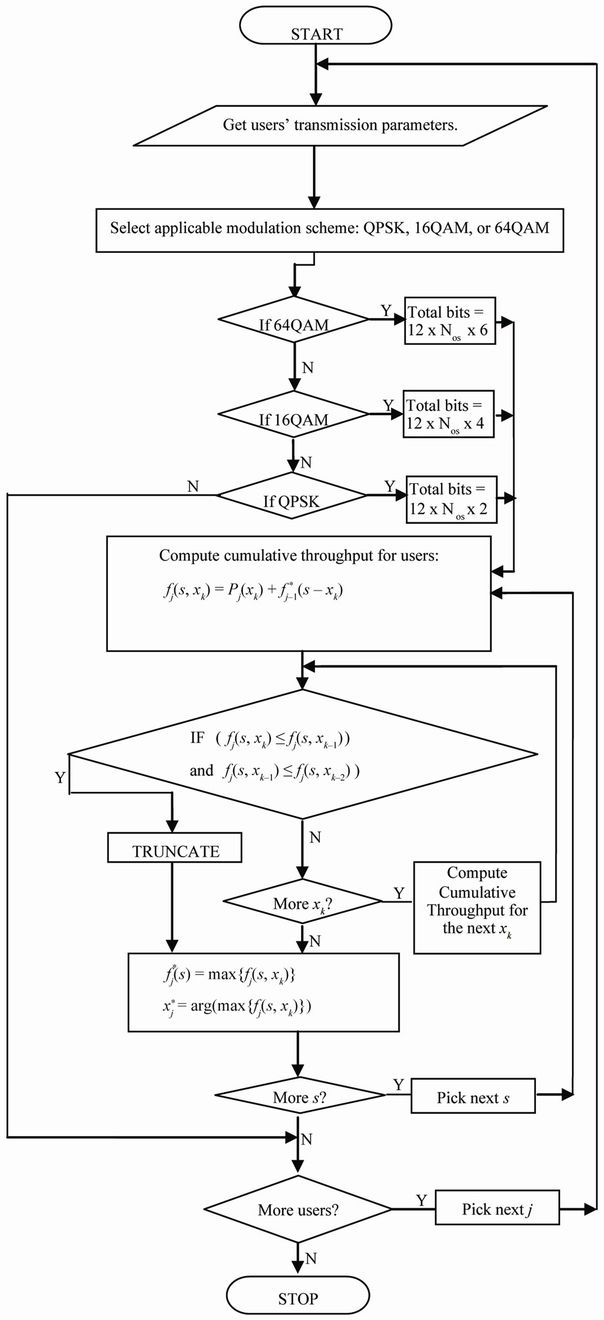
Figure 1. Systems flowchart.
3.2. Simulation Results
Simulation results for the proposed Truncated Dynamic Programming (TDP) under uncertainty are presented in Figures 2, 4 and 6. We also present comparative results for the corresponding Dynamic Programming (DP) based technique in Figures 3, 5 and 7.
We further compare the performance of the proposed TDP technique with that of the Fair Allocation technique. The instantaneous cumulative throughputs for both techniques, based on Options 1, 2 and 3, are presented in Tables 3-5 respectively. The Fair allocation technique ensures fairness in allocation of resources to network users independent of traffic characteristics. The technique requires that each network user is allocated some amount of available radio resource for transmission.
To ensure realistic comparison and fairness, we allocate 6 RBs to users with good signal strength (i.e., users using 64QAM modulation scheme) and 4 RBs to users with poor signal strength (i.e., users using 16QAM or
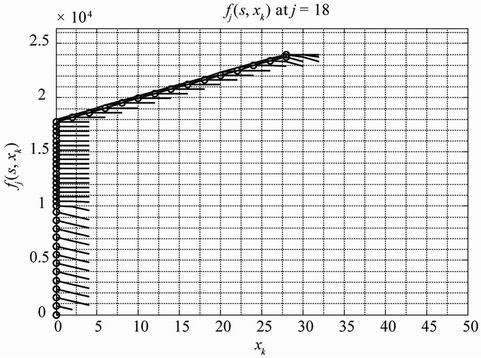
Figure 2. TDP—Option 1.

Figure 3. DP—Option 1.
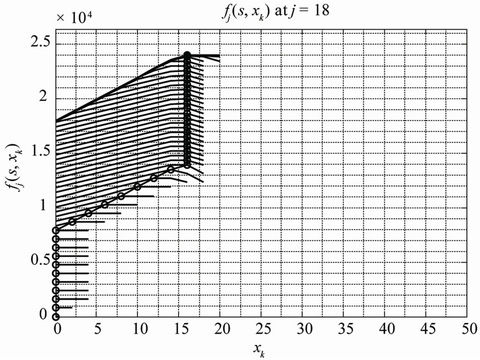
Figure 4. TDP—Option 2.
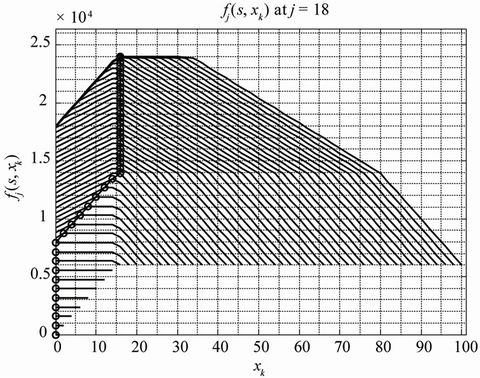
Figure 5. DP—Option 2.

Figure 6. TDP—Option 3.
QPSK modulation scheme).
The graphs showing comparative cumulative throughputs for the TDP and Fair Allocation techniques are presented in Figure 8.
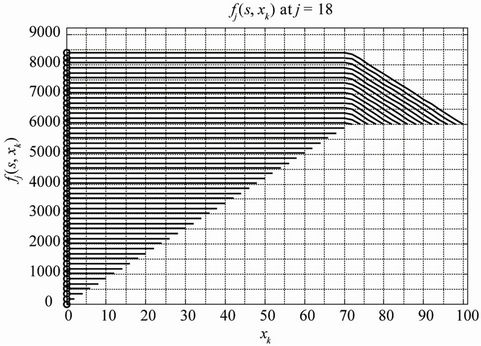
Figure 7. DP—Option 3.
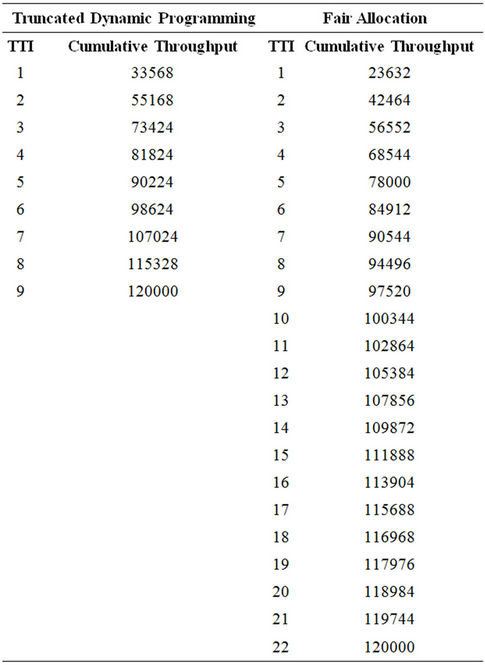
Table 3. Option 1.
4. Discussion of the Simulation Results
In the proposed truncated dynamic programming under uncertainty technique, the system can adapt dynamically to changing locations of users (corresponding to changing signal strength) as a result of users’ mobility. The computations of instantaneous cumulative throughputs are based on the applicable modulation scheme (i.e., QPSK, 16QAM or 64QAM). Since the location of user
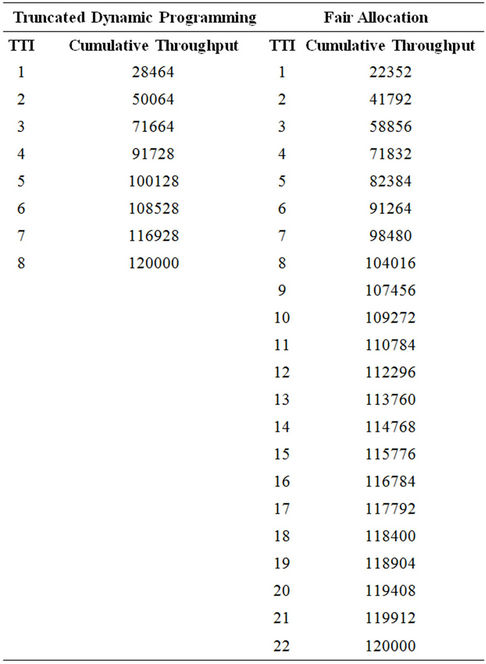
Table 4. Option 2.
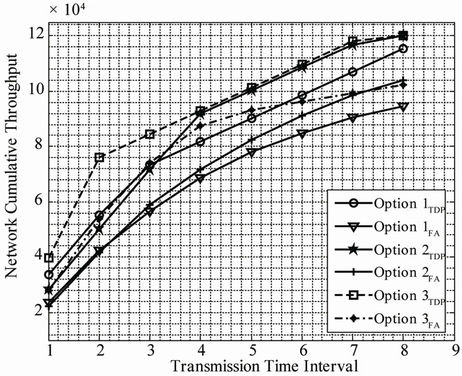
Figure 8. Network throughput for the Fair Allocation and Truncated Dynamic Programming based techniques.
within a Cell coverage area is uncertain, selection of applicable modulation scheme is also uncertain. Thus, the optimal decision at each stage can be taken only after the outcome of the uncertain event (i.e., selection of the applicable modulation scheme).
We note that for an optimal policy, whatever the current state and decision, the remaining decisions relating
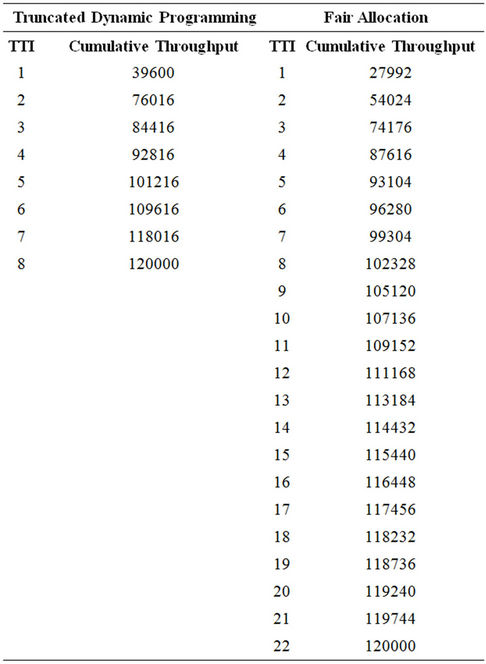
Table 5. Option 3.
to the resulting state from the current decision must be an optimal policy. The optimality of the proposed allocation scheme is assured by the applicable dynamic programming procedure. For the current work, the applicable dynamic programming procedure is the Back Induction (BI) process wherein the first stage to be analysed is the final stage of the problem and the n-stage problem is solved moving backwards one stage at a time until all stages are included to obtain optimal solution.
In this paper, we assume 20 network users within a Cell coverage area. Cells are geographical areas that are covered by radio signals from a Base Station. Allocated RBs ranges from 0 to 100, in multiples of 2 RBs (i.e., xk: 0, 2, 4, 6, …, 98, 100). In computing cumulative contributions using the proposed technique, the system compares current cumulative contribution with the last two preceding consecutive cumulative contributions. If the current computed cumulative contribution is less than or equal to the first preceding cumulative contribution and the first preceding cumulative contribution is less than or equal to the second preceding cumulative contribution, then further computations with respect to the chosen s (i.e., available RBs) are truncated. The system then picks the next available RBs (i.e., next s), and use possible allocated RBs (i.e., xk: 0, 2, 4, 6, …, 100) to compute cumulative contributions to the total throughput; while checking the truncation conditions. This recursive process continues for all available RBs (i.e., s), for all possible allocated RBs (i.e., xk) and for all scheduled users within a Cell coverage area.
Whereas the optimal decision on maximum cumulative contribution to the total throughput is taken at xk = 28 in Figure 2, and truncation is effected at xk = 32; same decision is taken in Figure 3 after computing cumulative contributions for all xk, (i.e., xk = 0, 2, …, 100). Similarly in Figure 4, the dynamic programming procedure is truncated after computing cumulative throughput (or contribution) for xk = 20, since maximum cumulative contribution is obtained at xk = 16. However, for the corresponding dynamic programming based graphs presented in Figure 5, the computations are carried out for all xk (i.e., xk = 0, 2, …, 100). In Figure 6 on the one hand, the truncated dynamic programming based graph is truncated at xk = 4, as the instantaneous maximum cumulative contribution is obtained at xk = 0. On the other hand, for the corresponding dynamic programming procedure in Figure 7, the computations are carried out for all xk (i.e., xk = 0, 2, …, 100).
To further confirm the effectiveness and efficiency of the proposed truncated dynamic programming technique, we compare its performance with the Fair Allocation technique. For the Fair allocation technique, 6 RBs are allocated to users with good signal strength and 4 RBs are allocated to users with poor signal strength. Relevant data on the comparative analysis are presented in Tables 3-5. The graphs in Figure 8 for Options 1, 2, and 3, show that the Truncated Dynamic Programming technique performs better than the Fair Allocation technique.
5. Conclusion
In this paper, we proposed a truncated dynamic programming under uncertainty based technique for efficient and optimal allocation of RBs in a multi-user Cellular LTE downlink. We gave the motivation for truncating the dynamic programming procedure, and also provided the effect of truncation on the recursive procedure. The simulation analysis was done under three different Options. In view of space constraint in this paper, we could not present results for all the twenty users (i.e. n = 20) considered, but we presented results for only the 18th user (i.e. j = 18). We could have taken any other user for our analysis. Furthermore, we compared the performance of the proposed truncated dynamic programming under uncertainty with the earlier proposed deterministic dynamic programming based technique. We also compared performance of the proposed technique with the Fair allocation technique. In terms of throughput, we found that the truncated dynamic programming based technique performed better than the Fair allocation methodology. Moreover, the Truncated Dynamic Programming and the earlier proposed Dynamic Programming based techniques achieved same throughput, but the Truncated Dynamic Programming based technique was more efficient as the computational time involved was significantly lower. Thus, it is shown by the results obtained that the proposed technique is more efficient in allocating radio resource and has better performance than both the Fair Allocation and deterministic dynamic programming based techniques for scheduling in Cellular LTE downlink. Besides, the proposed technique has the added advantage of managing uncertainty in selecting applicable modulation scheme (i.e., QPSK, 16QAM or 64QAM) as a result of users’ mobility within a Cell coverage area.
REFERENCES
- 3GPP TS 36.211. “Evolved Universal Terrestrial Radio Access (EUTRA); Physical Channel and Modulation (Release 8),” Technical Report, 3GPP-TSG R1, September 2007.
- O. Iosif and I. Banica, “On the Analysis of Packet Scheduling in Downlink 3GPP LTE System,” Proceedings of the 4th International Conference on Communication Theory, Reliability and Quality of Service, Budapest, 17-22 April 2011, pp. 99-102.
- H. Holma and A. Toskala, “LTE for UMTS: OFDMA and SC-FDMA Based Radio Access,” John Wiley & Sons, New York, 2009.
- J. Huang, V. G. Subramanian, R. Agrawal and R. A. Berry, “Downlink Scheduling and Resource Allocation for OFDM Systems,” IEEE Transactions on Wireless Communications, Vol. 8, No.1, 2009, pp. 288-296. doi:10.1109/T-WC.2009.071266
- M. S. Kaiser and K. M. Ahmed, “Radio Resource Allocation for Heterogeneous Services in Relay Enhanced OFDMA Systems,” Journal of Communications, Vol. 5, No. 6, 2010, pp. 447-454.
- A. Wang, Y.-Y. Qiu, L. Lin and S. Li, “An Adaptive Sub-Carrier and Power Allocation Algorithm with QoS Guarantee for OFDMA System,” 10th IEEE Conference on High Performance Computing and Communications, Dalian, 25-27 September 2008, pp. 492-497.
- G. H. Kumar, P. H. Krishnarao and K. S. R. Krishna, “Two-Stage Algorithm for Sub-Carrier, Bit and Power Allocation in OFDMA Systems,” International Journal of Computer Science and Communications, Vol. 1, No. 2, 2010, pp. 51-54.
- G. Li and H. Liu, “Downlink Radio Resource Allocation for Multi-Cell OFDMA System,” IEEE Transactions on Wireless Communications, Vol. 5, No. 12, 2006, pp. 3451- 3459. doi:10.1109/TWC.2006.256968
- I. Koutsopoulos and L. Tassiulas, “Cross-Layer Adaptive Techniques for Throughput Enhancement in Wireless OFDM-Based Networks,” IEEE/ACM Transactions on Networking, Vol. 14, No. 5, 2006, pp. 1056-1066. doi:10.1109/TNET.2006.882842
- T. Thonabalasinghan, S. Hanley, L. L. H. Andrew and J. Papandripoulos, “Joint Allocation of Sub-Carriers and Transmit Powers in a Multi-User OFDM Cellular Network,” IEEE International Conference on Communications, Istanbul, 11-15 June 2006, pp. 269-274. doi:10.1109/ICC.2006.254739
- C. Koutsimanis and G. Fodor, “A Dynamic Resource Allocation Scheme for GBR Services in OFDMA Networks,” Proceedings of the IEEE Conference of Communications, Beijing, 19-23 May 2008, pp. 2524-2530.
- I. C. Wong and B. L. Evans, “Optimal Resource Allocation in OFDMA Systems with Imperfect Channel Knowledge,” IEEE Transactions on Communications, Vol. 57, No. 1, 2009, pp. 232-241. doi:10.1109/TCOMM.2009.0901.060546
- P. Hosein, “Coordinated Radio Resource Management for the LTE Downlink: The Two-Sector Case,” IEEE International Conference on Communications, Cape Town, 23-27 May 2010, pp. 1-5.
- N. Zhou, X. Zhu and Y. Huang, “Genetic Algorithm Based Cross-Layer Resource Allocation for Wireless OFDM Networks with Heterogeneous Traffic,” 17th European Signal Processing Conference (EUSIPCO), Glasgow, 24- 28 August 2009, pp. 1656-1659.
- M. Ergen, S. Coleri and P. Varaiya, “QoS Aware Adaptive Resource Allocation Techniques for Fair Scheduling in OFDMA Based Broadband Wireless Access Systems,” IEEE Transactions on Broadcasting, Vol. 49, No. 4, 2003, pp. 362-370. doi:10.1109/TBC.2003.819051
- A. M. Ajofoyinbo and K. Orolu, “A Dynamic Programming Based Technique for Optimal Allocation of Radio Resource in Multi-User Cellular Long-Term Evolution (LTE) Downlink,” 10th WSEAS International Conference on Telecommunications and Informatics (TELE-INFO’11), Lanzarote, Spain, 27-29 May 2011, pp. 107-113.
- F. S. Hillier and G. J. Lieberman, “Introduction to Mathematical Programming,” 2nd Edition, McGraw-Hill Inc., New York, 1995.

