Journal of Intelligent Learning Systems and Applications
Vol.5 No.2(2013), Article ID:31488,8 pages DOI:10.4236/jilsa.2013.52013
Face Recognition Based on Wavelet Packet Coefficients and Radial Basis Function Neural Networks
![]()
1Department of Computer Science, Virudhunagar Hindu Nadars’ Senthikumara Nadar College, Virudhunagar, India; 2Department of Computer Applications, Ayya Nadar Janaki Ammal College, Sivakasi, India.
Email: *kathirvalavakumar@yahoo.com, jebaarul07@yahoo.com
Copyright © 2013 Thangairulappan Kathirvalavakumar, Jeyasingh Jebakumari Beulah Vasanthi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 12th, 2012; revised April 19th, 2013; accepted April 26th, 2013
Keywords: Feature Extraction; Face Recognition; Wavelet Packets; Radial Basis Function Neural Network
ABSTRACT
An efficient face recognition system with face image representation using averaged wavelet packet coefficients, compact and meaningful feature vectors dimensional reduction and recognition using radial basis function (RBF) neural network is presented. The face images are decomposed by 2-level two-dimensional (2-D) wavelet packet transformation. The wavelet packet coefficients obtained from the wavelet packet transformation are averaged using two different proposed methods. In the first method, wavelet packet coefficients of individual samples of a class are averaged then decomposed. The wavelet packet coefficients of all the samples of a class are averaged in the second method. The averaged wavelet packet coefficients are recognized by a RBF network. The proposed work tested on three face databases such as Olivetti-Oracle Research Lab (ORL), Japanese Female Facial Expression (JAFFE) and Essex face database. The proposed methods result in dimensionality reduction, low computational complexity and provide better recognition rates. The computational complexity is low as the dimensionality of the input pattern is reduced.
1. Introduction
Recognition of human faces is a very important task in many applications such as authentication and surveillance. A variety of changes in face images also a great challenge. A face recognition system must be robust with respect to the much variability of face images such as viewpoint, illumination, and facial expression. The two main tasks in the face recognition system are representation of face and classification of the face.
Many methods have been proposed for face recognition [1] in which appearance-based approaches operates directly on images or appearances of face objects. Turk and Pentland have implemented the Eigenfaces approach [2] which is the popular face recognition method. The approach transforms face images into a small set of characteristic feature images, called eigenfaces, which are the principal components of face images. Linear Discriminant Analysis (LDA) could be operated either on the raw face image to extract the Fisherface [3] or on the eigenface to obtain the discriminant eigen features [4]. Jian Yang et al. have developed a new technique coined two-dimensional principal component analysis (2DPCA) for image representation. As opposed to PCA, 2DPCA is based on 2D image matrices rather than 1D vector so the image matrix does not need to be transformed into a vector prior to feature extraction [5]. Rajagopalan et al. have proposed face recognition system using multiple facial features extracted from the face [6].
Image representation is an essential technique in many image processing tasks. Wavelet based image representation has many advantages. An appropriate wavelet transform can result in robust representation with regard to lighting changes and be capable of capturing substantial facial features while keeping computational complexity low. Bai-Ling Zhang et al. have proposed to use Wavelet Transform (WT) to decompose face images and choose the lowest resolution subband coefficients for face representation [7]. Wavelet Packet Decomposition (WPD) of an image is a useful technique for building compact and meaningful feature vector and is also used in face recognition [8]. Wavelet packet decomposition is extended from the wavelet decomposition. It includes multiple bases and different basis which result in different classification performance and cover the shortage of fixed time-frequency decomposition [9].
Ognian Boumbarov et al. have proposed a method in which, wavelet packets are used for dimensionality reduction [10]. Vytautas Perlibakas [11] has presented a work on face recognition using both principal component analysis and wavelet packet decomposition.
In the face recognition process, classifier plays a crucial role. Conventional classifiers and neural networks have been employed in classification. Chien and Wu [12] have proposed a hybrid approach, in which, the nearest feature plane (NFP) and nearest feature space (NFS) classifiers are explored for robust decision in the presence of wide facial variations. The mostly adopted network topology is radial basis function neural network (RBFNN) due to a number of advantages compared with other types of ANNs, such as better prediction capabilities, simpler network structures, and faster learning process [13]. Radial Basis Function neural networks (RBF) are suitable for pattern recognition and classification. Hai Guo and Jing-ying Zhao have proposed Chinese minority script recognition using radial basis function network [14]. Many researchers have implemented face recognition system using RBF neural network [15,16]. Bicheng Li and Hujun Yin have presented a face recognition system using radial basis function neural network and wavelet transformation [17]. Ning Jin and Derong Liu have developed wavelet basis function neural networks (WBFNN) with sequential learning algorithm and compared it with the sequential learning algorithm of RBF neural network [18].
In this paper, a face recognition system using the radial basis function neural network which recognizes the averaged wavelet packet is proposed. The wavelet packet transform is used to decompose input patterns and the resulting wavelet packet coefficients are averaged for a single pattern or for a class of patterns and then considered for recognition. The rest of the paper is structured as follows: Section 2 describes preprocessing. Section 3 presents the recognition process using radial basis function neural network. Section 4 describes the experiment results along with discussions.
2. Preprocessing
Using the wavelet transformation, the image is decomposed into the approximation and detailed coefficients. The approximation coefficient only is then decomposed into a second level of approximation and detailed coefficients. In the wavelet packet transformation, each approximation coefficients as well as detailed coefficients of the face are decomposed as in Figure 1.
The original image 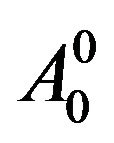 of level 0 is decomposed into approximation
of level 0 is decomposed into approximation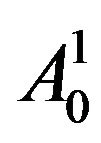 , horizontal details
, horizontal details , vertical details
, vertical details 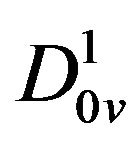 and diagonal details
and diagonal details 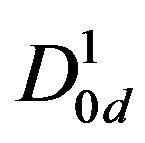 at level 1. The approximation
at level 1. The approximation 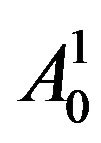 is further decomposed into the nodes such as
is further decomposed into the nodes such as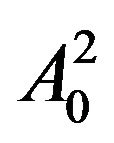 ,
, 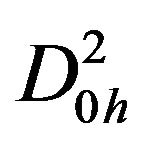 ,
, 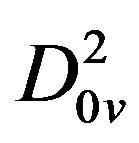 ,
, 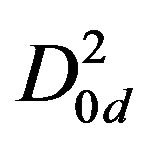 in the level 2. Likewise, horizontal, vertical and diagonal details are decomposed into the nodes such as
in the level 2. Likewise, horizontal, vertical and diagonal details are decomposed into the nodes such as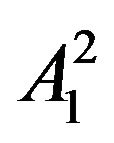 ,
, 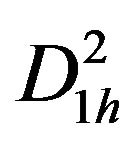 ,
, 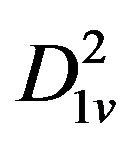 ,
, 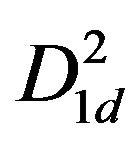 ,
, 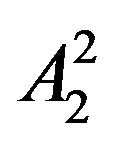 ,
, 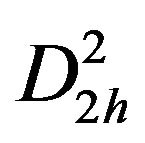 ,
, 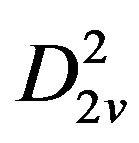 ,
, 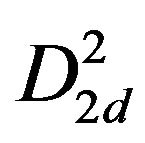 ,
, 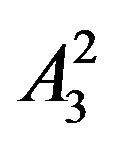 ,
, 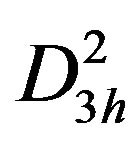 ,
,  and
and 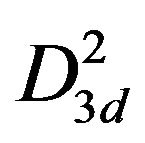 respectively.
respectively.
In order to get decomposition at level l, decompose the approximations 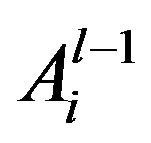 and details
and details ,
,  ,
, 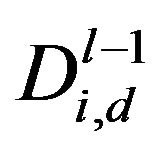 as follows as proposed by Perlibakas [11]:
as follows as proposed by Perlibakas [11]:
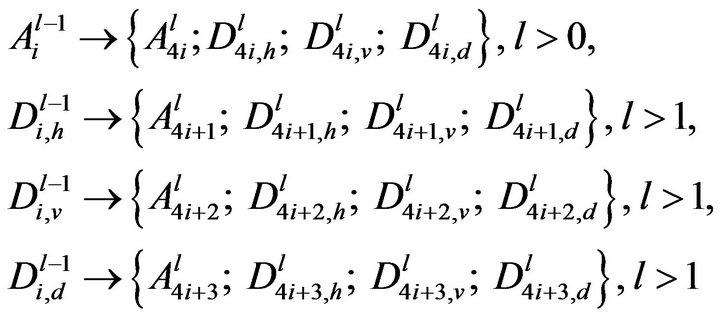 (1)
(1)
where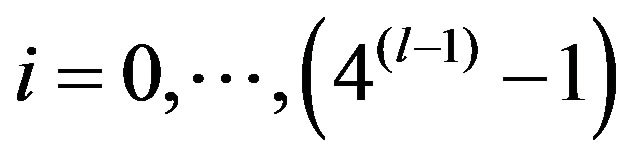 .
.
During the wavelet transformation, at level 2, only the approximation is decomposed into approximation and details. The wavelet packet transformation has been applied on the face images for two levels and obtains the four wavelet packet coefficients namely approximation, horizontal details, vertical details, and diagonal details. The obtained wavelet packets are processed using two different methods and the resultant is used as an input for recognition.
2.1. Method I
In the first method, the approximation coefficients represented in the tree nodes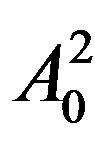 ,
,  ,
, 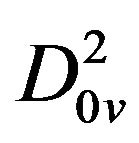 ,
, 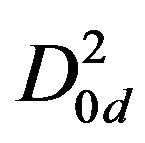 are added and the values are averaged. Wavelet packet decomposition is applied on the averaged approximation coefficients. The decomposed averaged approximation coefficients are supplied as input to the recognition process.
are added and the values are averaged. Wavelet packet decomposition is applied on the averaged approximation coefficients. The decomposed averaged approximation coefficients are supplied as input to the recognition process.
The first method is summarized as follows:
1) Do the steps 2 - 4 for all the training samples.
2) Apply wavelet packet transformation for two levels

Figure 1. Wavelet packet tree.
and compute the wavelet packet coefficients for the sample.
3) Add the four child nodes of 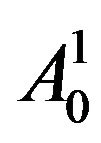 and compute the averaged wavelet packet coefficients.
and compute the averaged wavelet packet coefficients.
4) Apply wavelet packet transformation on the averaged wavelet packet coefficients.
5) Enter decomposed averaged approximation wavelet packet coefficients of each sample as an input to the RBF network.
6) Train the RBF network using the training algorithm given in Section 3.1.
7) Compute the averaged and decomposed wavelet packet coefficients for testing samples and recognize it through trained RBF.
2.2. Method II
In this method, the approximation coefficients obtained for each face image of a class in a training set are averaged and then average the averaged coefficients of each image of a class. This process is repeated for all classes of the training set. Then average the decomposed coefficients obtained from all the classes are applied as input to the recognition process. The second method is summarized as follows:
1) Apply 2-level wavelet packet transformation on a sample of a class of training set and compute the wavelet packet coefficients.
2) Add the four nodes of 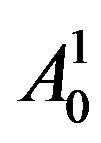 namely
namely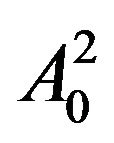 ,
, 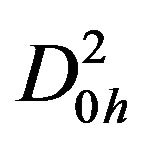 ,
, 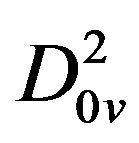 ,
, 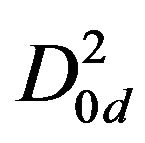 and compute its average.
and compute its average.
3) Repeat steps 1 and 2 for all the training samples of the class.
4) Find the average of averaged approximation wavelet coefficients of the class.
5) Repeat steps 1 to 4 for all classes.
6) Use the averaged approximation wavelet coefficients obtained for each class as input patterns to the RBF network.
7) Train the RBF network using the training algorithm given in Section 3.1.
8) Compute the averaged approximation wavelet packet coefficients for testing samples and recognize it through the trained RBF.
A significant part of a face recognition process is the feature extraction and dimensionality reduction of a given facial image. In the proposed work, two level wavelet packet decompositions applied on input samples results in 4 approximation coefficients and 12 detailed coefficients totally 16 wavelet packet coefficients. The wavelet packets have extracted the substantial facial features from the input sample images. In order to get compact and meaningful features, the 4 approximation coefficients are averaged in two different manners using the two proposed methods. In the first method, the four approximation coefficients are averaged and decomposed to produce reduced and meaningful coefficients. In order to reduce the number of input patterns, the wavelet packet coefficients are averaged with respect to each class in the second method.
3. Recognition by Radial Basis Function Neural Network
Radial Basis Function neural network (RBF) considered for recognition of wavelet packet coefficients contains three layers: input, hidden and output. The number of nodes in the input layer corresponds to the dimension of wavelet packet coefficients. The input neurons are normalized using the following equation:
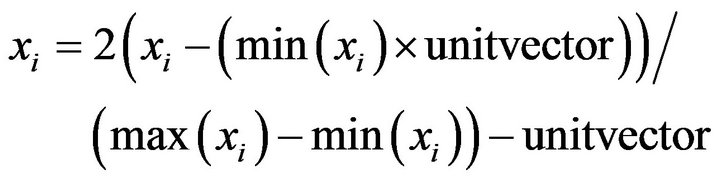 (2)
(2)
where  is the ith input vector.
is the ith input vector.
The normalized inputs values are fed to each of the neurons in the hidden layer. The basis functions of the hidden layer neurons are considered to be Gaussian and computed basis function outputs are passed to the output layer.
The hidden layer output is computed as
 (3)
(3)
where 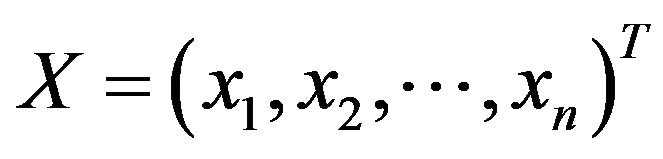 is the normalized input vector,
is the normalized input vector, 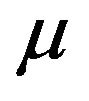 is the center and
is the center and  is the width.
is the width.
The output layer output is computed as
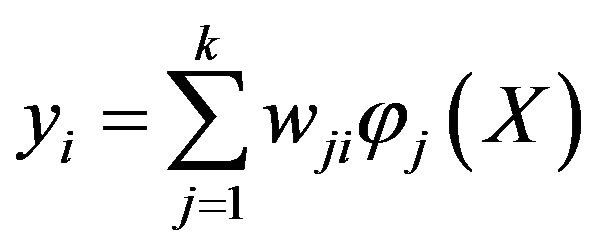 (4)
(4)
where  is the number of hidden neurons,
is the number of hidden neurons, 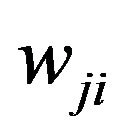 are the weights connecting the hidden layer neuron and output layer neuron. The weights are adjusted using the formula,
are the weights connecting the hidden layer neuron and output layer neuron. The weights are adjusted using the formula,
 (5)
(5)
where 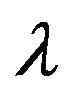 is a positive learning rate parameter and di is the desired output.
is a positive learning rate parameter and di is the desired output.
Algorithm
The training algorithm of Radial Basis Function Network is given as follows.
Step 1. Generate random numbers to initialize the weights of the RBF network.
Step 2. Enter the computed averaged approximation wavelet packet coefficients and expected output values.
Step 3. For each input pattern, compute hidden layer output using Equation (3).
Step 4. Compute the output layer output using Equation (4).
Step 5. Find the error as the difference between desired and obtained actual output.
Step 6. Adjust the hidden layer weights according to Equation (5).
Step 7. Find output of the output layer.
Step 8. Compute sum of squared error of the network.
Step 9. Repeat steps 3 - 8 for all input patterns.
Step 10. Repeat steps 3 - 9 until the acceptable minimum error level is reached.
4. Results and Discussions
The proposed work has been carried out using Matlab 7.1 and tested using the face databases such as Olivetti-Oracle Research Lab (ORL), the Japanese Female Facial Expression (JAFFE) and the Essex face database. Figures 2(a) and (b) show the respective result of an image after applying the wavelet transform and wavelet packet transform for two levels.
The ORL face data base contains 40 faces and each face has 10 different facial views representing various expressions, small occlusion by glasses, different scale and orientations. Hence, there are 400 face images in the database and each 100 images of 20 persons are used for
 (a)
(a) (b)
(b)
Figure 2. (a) 2-level wavelet decomposition; (b) 2-level wavelet packet decomposition.
training and another 100 images of the 20 persons are used for testing. The resolution of all the images is 112 × 92. Different wavelets namely Haar, Symlet, Daubechies and Coiflets are used during wavelet packet decomposition. The original image and the averaged decomposed image obtained using the first method is shown in Figure 3. The recognition rates are obtained by doing the training and testing process repeatedly for 20 times and averaged. The computed recognition rates along with training time, epoch and decomposed input vector size obtained while using Method I are shown in Table 1. The recognition rate for Haar wavelet is 97% which is the highest one and the lowest recognition rate of 90% is obtained for the Sym8 wavelet. The lowest decomposed vector size 644 has been obtained for Haar wavelet after 2-level wavelet packet transformation. The averaged wavelet packet images obtained by the proposed second method are shown in Figure 4 for some images, along with its original sample image. The results such as recognition rates, training time, epoch and decomposed input vector size obtained from Method II are shown in Table 2. The recognition rates for different wavelets namely Haar, Sym4, Sym8, Db4, Db6, Coif2, Coif4 are 96%, 92%, 90%, 94%, 91%, 95% and 92% respectively.
When comparing the proposed two methods, there are not much variations in the recognition rates. The training time is less for the second method because the number of input patterns is reduced due to the averaging of the wavelet packet coefficients with respect to each class. The actual size of the input vector 10304 has been reduced to the dimensions 644, 924, 1326, 1116 and 1800


Figure 3. Original sample image and averaged decomposed image—Method I.
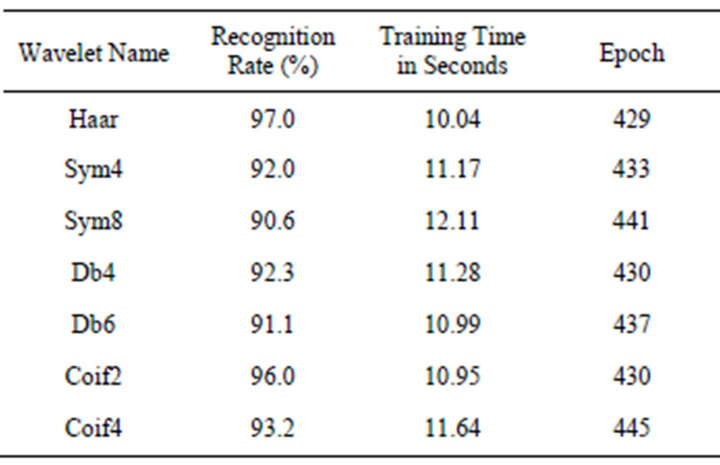
Table 1. Recognition rate, training time, epoch—Method I.










Figure 4. Original samples and averaged image—Method II.
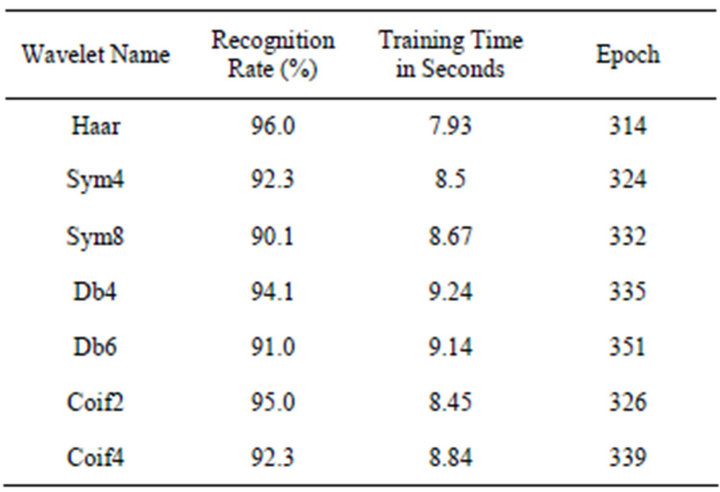
Table 2. Recognition rate, training time, epoch—Method II.
respectively for the wavelets namely Haar, Sym4, Sym8, Db6 and Coif4 after applying two level wavelet packet transformation.
The Japanese Female Facial Expression contains different facial expressions posed by Japanese female models in which 5 different poses of 15 models are used for training and the other 5 different poses of 15 models are used for testing. The actual dimension of the image is 256 × 256. The averaged approximation wavelet packet coefficients obtained by the two proposed methods are used as input to the RBF network. The RBF network is trained for different learning rate parameter. The actual size of the input vector 65536 has been reduced to 4096, 4761, 5625, 4761, 5184, 5184, 6561 respectively when Haar, Sym4, Sym8, Db4, Db6, Coif2, Coif4 wavelets are used in wavelet packet decomposition. The epoch, training time and recognition rate obtained for JAFFE Database from the Method I are listed in Table 3. The recognition rates 97% for Haar wavelet and 96% for Sym8 and Coif4 are obtained. Lowest training time 37.68 seconds is obtained when Haar wavelet is applied. When the wavelet packet transformation is performed using the Coif4 wavelet, it takes the highest training time as 51.27 seconds. The Recognition rate, training time, epoch and input vector size obtained for JAFFE database by the Method II are shown in Table 4. The highest rate of recognition is 96% for Haar wavelet and the lowest rate is 90% for Sym8 wavelet.
The Essex Face database is having faces of more than 150 male and female with 20 images per individual of University of Essex, UK with the size of 180 × 200. The 5 different poses of 20 person’s face are used for the training and 5 different poses of 20 person’s faces are used for the testing in the proposed methods. The wavelet packets coefficients are obtained for the samples and recognition process is applied for the obtained averaged wavelet packet coefficients. Figure 5 shows some sample images of Essex face database. The decomposed image using Haar is shown in Figure 6. The decomposed image after applying Coif4 wavelet shown is in Figure 7. The various results obtained from the two proposed methods on Essex face database are presented in Tables 5 and 6. Among the levels of wavelet packet decomposition, the two level decomposition yields better recognition accuracy.
In the first method, the recognition rate 97% has been achieved for Db6 wavelet and Sym4 but Coif4 wavelets result in 93%. The two methods are tested on the ORL, JAFFE and Essex face databases using different types of
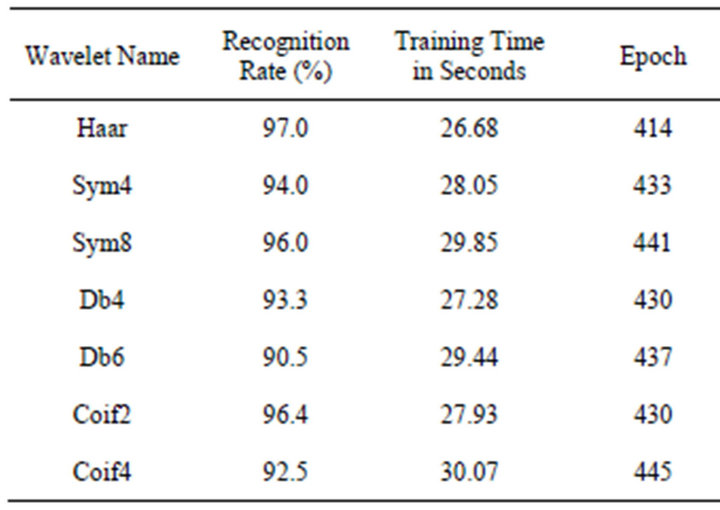
Table 3. Results of JAFFE database—Method I.

Table 4. Results of JAFFE database—Method II.





Figure 5. Sample images of Essex face database.





Figure 6. Decomposed image for Haar wavelet.





Figure 7. Decomposed image by applying Coif4 wavelet.
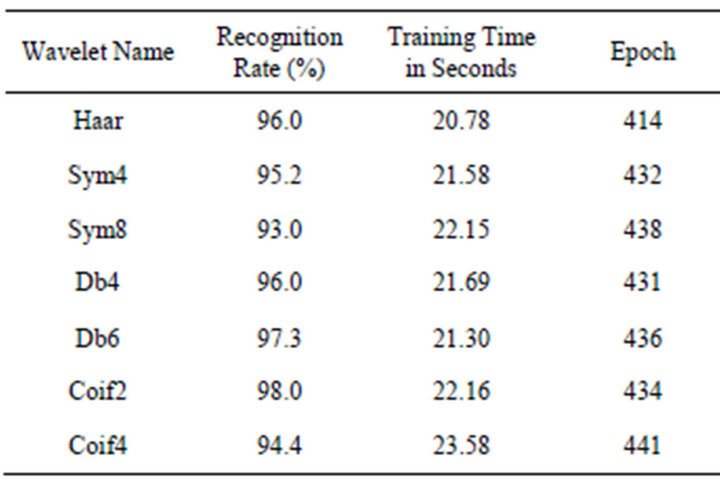
Table 5. Results of Essex database—Method I.
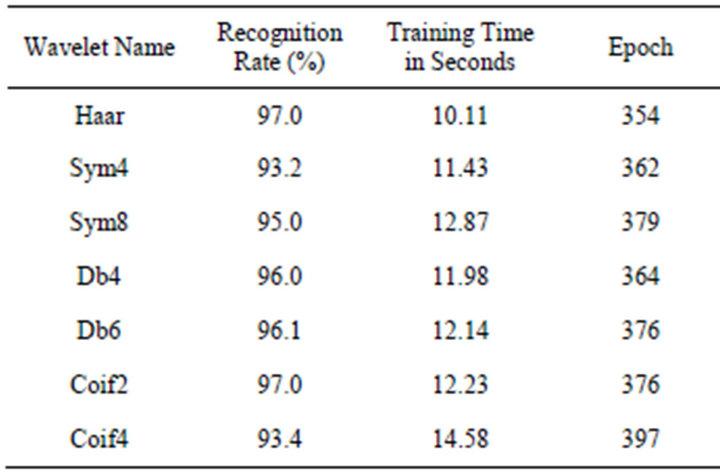
Table 6. Results of Essex database—Method II.
wavelets and the comparative results are shown in Figure 8 for the first method. Figure 9 compares the results obtained by the second method. The recognition rates obtained using the three face databases on other methods and with the proposed methods are shown in Table 7.
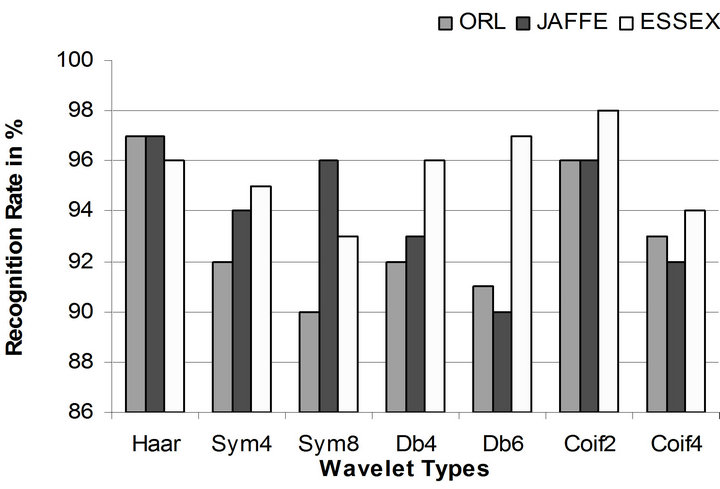
Figure 8. Comparison of recognition rate—Method I.
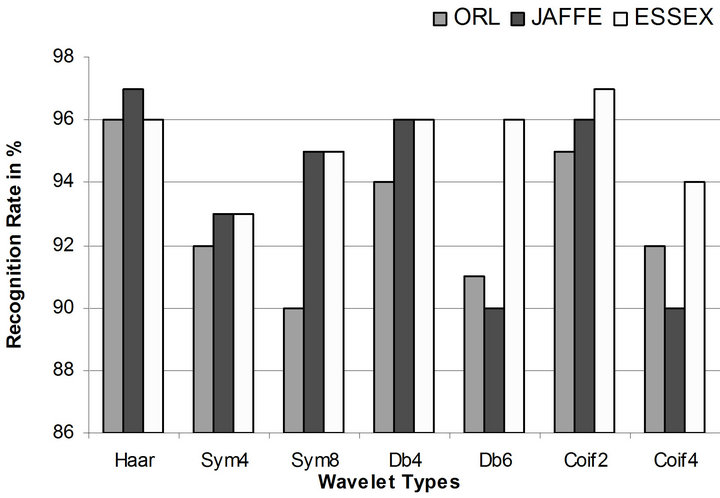
Figure 9. Comparison of recognition rate—Method II.
The recognition rate of 97% is obtained by the Hidden Markov Model (HMM) method on ORL database. The MLA + NM method has the recognition rate of 97% on JAFFE database. When ESSEX database is used, the recognition rate of 92.63% has been achieved by fisher faces method. Eigen face, wavelet face and SOM methods have better results when combined with neural networks (NN) or convolution neural networks.
RBF neural networks (RBFNN) have been used for face recognition and the results obtained by other methods are compared with the two proposed methods and are shown in Table 8. The recursive orthogonal least square algorithm (ROLSA), particle swarm optimization (PSO) and minimum volume covering hyperspheres (MVCH) have been used to train and optimize the RBFNN structure with considerable success [19]. Face recognition system based on Fisher’s linear discriminant (FLD) with RBF and Kernal Fisher’s linear discriminant (KFLD) with RBF [20] obtained recognition rates as 94.9% and 95.7% respectively when tested on ORL database.
5. Conclusion
A face recognition system with effective face representa-
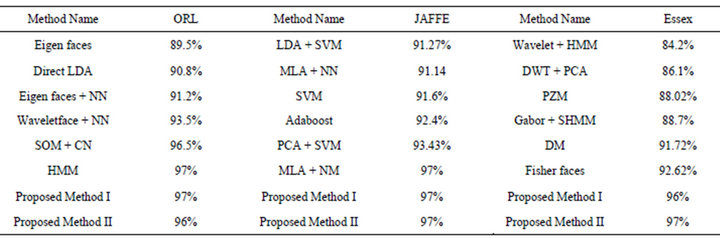
Table 7. Comparison of recognition rates.
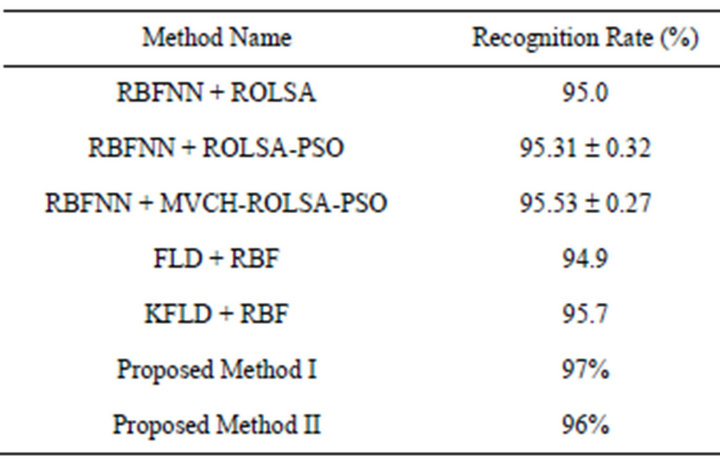
Table 8. RBF based face recognition rates for ORL.
tion using averaged approximation wavelet packet coefficients and recognition by radial basis function (RBF) neural network is proposed. The size of input patterns is reduced using wavelet packet transformation. The wavelet packet transformation is initially applied on the input patterns to obtain wavelet packet coefficients. The obtained wavelet packets are tuned by taking its average and decomposition. The average of averaged wavelet packets obtained according to each class is resulted in better dimensionality reduction. The minimized patterns of each class represent all features of the whole datasets. The recognition rate is not affected by the dimensionality reduction but the training time is reduced in the second method. Various types of wavelets are used in the wavelet packet transformation. Each type of wavelet results in different size of decomposed vector. The reduced wavelet packets are recognized by radial basis function network. The proposed work yields good recognition rate.
REFERENCES
- W. Zhao, R. Chellappa, A. Rosenfeld and P. J. Phillips, “Face Recognition: A Literature Survey,” Technical Report CAR-TR-948, University of Maryland, College Park, 2000.
- M. Turk and A. Pentland, “Eigenfaces for Recognition,” Cognitive Neuroscience, Vol. 3, No. 1, 1991, pp. 71-86. doi:10.1162/jocn.1991.3.1.71
- P. Belhumeur, J. Hespanha and D. Kriegman, “Eigenfaces vs Fisher Faces: Recognition Using Class Specific Linear Projection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 20, No. 7, 1997, pp. 711-720. doi:10.1109/34.598228
- D. L. Swets and J. Weng, “Using Discriminant Eigenfeatures for Image Retrieval,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 18, No. 8, 1996, pp. 831-836. doi:10.1109/34.531802
- J. Yang, D. Zhang, A. F. Frangi and J.-Y. Yang, “TwoDimensional PCA: A New Approach to AppearanceBased Face Representation and Recognition,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 26, No. 1, 2004, pp. 131-138. doi:10.1109/TPAMI.2004.1261097
- A. N. Rajagopalan, K. S. Rao and Y. A. Kumar, “Face Recognition Using Multiple Facial Features,” Pattern Recognition Letters, Vol. 28, No. 3, 2007, pp. 335-341. doi:10.1016/j.patrec.2006.04.003
- B.-L. Zhang, H. H. Zhang and S. Z. S. Ge, “Face Recognition by Applying Wavelet Subband Representation and Kernel Associative Memory,” IEEE Transactions on Neural Networks, Vol. 15, No. 1, 2005, pp. 166-177. doi:10.1109/TNN.2003.820673
- C. Garcia, G. Zikos and G. Tziritas, “Wavelet Packet Analysis for Face Recognition,” Image and Vision Computing, Vol. 18, No. 4, 2000, pp. 289-297. doi:10.1016/S0262-8856(99)00056-6
- J. Z. Xue, H. Zhang and C. X. Zheng, “Wavelet Packet Transform for Feature Extraction of EEG during Mental Tasks,” Proceedings of the Second International Conference on Machine Learning and Cybernetics, Vol. 1, 2003, pp. 360-363.
- O. Boumbarov, S. Sokolov and G. Gluhchev, “Combined Face Recognition Using Wavelet Packets and Radial Basis Function Neural Network,” International Conference on Computer Systems and Technologies—CompSysTech’07, Bulgaria, 14-15 June 2007, pp. v.4.1-v.4.7.
- V. Perlibakas, “Face Recognition Using Principal Component Analysis and Wavelet Packet Decomposition,” Informatica, Vol. 15, No. 2, 2004, pp. 243-250.
- J.-T. Chien and C.-C. Wu, “Discriminant Waveletfaces and Nearest Feature Classifiers for Face Recognition,” IEEE Transactions on Pattern analysis and Machine Intelligence, Vol. 24, No. 12, 2002, pp. 1644-1649. doi:10.1109/TPAMI.2002.1114855
- T. M. Mitchell, “Machine Learning,” China Machine Press, Beijing, 2003.
- H. Guo and J.-Y. Zhao, “Chinese Minority Script Recognition Using Radial Basis Function Network,” Journal of Computers, Vol. 5, No. 6, 2010, pp. 927-934.
- X.-Y. Jing, Y.-F. Yao, J.-Y. Yang and D. Zhang, “A Novel Face Recognition Approach Based on Kernel Discriminative Common Vectors (KDCV) Feature Extraction and RBF Neural Network,” Neurocomputing, Vol. 71, No. 13-15, 2008, pp. 3044-3048. doi:10.1016/j.neucom.2007.08.027
- M. J. Er, S. Q. Wu, J. W. Lu and H. L. Toh, “Face Recognition with Radial Basis Function (RBF) Neural Networks,” IEEE Transactions on Neural Networks, Vol. 13, No. 3, 2002, pp. 697-710. doi:10.1109/TNN.2002.1000134
- B. C. Li and H. J. Yin, “Face Recognition Using RBF Neural Networks and Wavelet Transform,” Lecture Notes in Computer Science, Vol. 3497, 2005, pp. 105-111.
- N. Jin and D. R. Liu, “Wavelet Basis Function Neural Networks for Sequential Learning,” IEEE Transactions on Neural Networks, Vol. 19, No. 3, 2008, pp. 523-528. doi:10.1109/TNN.2007.911749
- D.-S. Huang and J.-X. Du, “A Constructive Hybrid Structure Optimization Methodology for Radial Basis Probabilistic Neural Networks,” IEEE Transactions on Neural Networks, Vol. 19, No. 12, 2008, pp. 2099-2115. doi:10.1109/TNN.2008.2004370
- Z.-Q. Zhao, D.-S. Huang and B.-Y. Sun, “Human face Recognition Based on Multi-Features Using Neural Networks Committee,” Pattern Recognition Letters, Vol. 25 No. 12, 2004, pp. 1351-1358. doi:10.1016/j.patrec.2004.05.008
NOTES
*Corresponding author.

