Journal of Intelligent Learning Systems and Applications
Vol.4 No.1(2012), Article ID:17557,11 pages DOI:10.4236/jilsa.2012.41006
An Intelligent Assessment Tool for Students’ Java Submissions in Introductory Programming Courses
![]()
Computer Science Department, College of Sciences, University of Sharjah, Sharjah, United Arab Emirates.
Email: fmalshamsi@sharjah.ac.ae, ashraf@sharjah.ac.ae
Received June 7th, 2011; revised July 8th, 2011; accepted July 18th, 2011
Keywords: Java; Programming; Computer Aided Education; Computer Aided Assessment; Control Dependence Graphs
ABSTRACT
This paper presents a graph-based grading system for Java introductory programming courses, eGrader. This system grades submission both dynamically and statically to ensure a complete and through grading job. While dynamic analysis is based on JUnit framework, the static analysis is based on the graph representation of the program and its quality which is measured by software metrics. The graph representation is based on the Control Dependence Graphs (CDG) and Method Call Dependencies (MCD). eGrader outperforms existing systems in two ways: the ability of grading submission with semantic-errors, effectively, and generating reports for students, as a feedback on their performance, and instructors on the overall performance of the class. eGrader is well received by instructors not only for saving time and effort but also for its high success rate that is measured by four performance indicators which are sensitivity (97.37%), specificity (98.1%), precision (98.04%) and accuracy (97.07%).
1. Introduction
The idea of making the process of grading programming assignments automatic started with teaching programming. In 1960’s, Hollingsworth [1] introduced one of the earliest systems which grade students programs written in Assembly language. Since then, the development and implementation of Automatic Programming Assignment Grading (APAG) systems has been a subject of great interest to many researchers. The need for decreasing the load of the work on the grader, timely feedback for the students and accuracy on the grading results are some of the reasons that motivated the need for APAG systems.
eGrader has been developed to grade solutions in Java programming courses. Java language is the most widely used language in teaching programming in introductory courses. Its popularity stems from the fact that it is a programming language that can do almost anything a traditional programming language like Fortran, Basic or C++ can do. It is considerably easier to program and to learn than those languages without giving up any of their power. Besides, developing the system using Java makes the resulting software truly portable across multiple machine architectures.
Although several automatic and semi-automatic programming grading systems were proposed in the literature, few of them can handle semantic errors in code. Besides, most of the existing systems are mainly concerned with the students’ scores ignoring other aspects.
This paper presents a new system, eGrader, for grading Java students’ solutions, both dynamically and statically, in introductory programming courses. Reports generated by eGrader make it a unique system not only to grade students’ submissions and provide them with detailed feedback but also to assist instructors in constructing a database of all students work and produce proper documents such as outcome analysis. In addition, eGrader is one of the few systems that can handle Java source code with the existence of semantic errors.
The remainder of the paper is organized as follows: Section 2 summarizes the existing APAG systems. Section 3 discusses the methodology adopted in eGrader. Components of eGrader framework are described in Section 4. In Section 5, we discuss the experimental results. We conclude the work and present possible future directions in Section 6.
2. Related Work
Computer aided education (CAE) grows with a great interest and is highly dependent on modern technology. CAE tools can be categorized as: computer aided learning (CAL) and computer aided assessment (CAA). CAL tools had proved to be effective in computer science education. For example, they had been used successfully in teaching and learning graphic structure with its algorithms [2], operating system courses [3], data structure courses [4], and core programming courses [5,6]. CAL tools also support distance learning through mobile learning (m-learning) technology [7,8]. CAA tools are introduced to complement CAL. It includes electronic quizzes and surveys [9,10], plagiarism and text reuse detection systems, and APAG systems. For example, JPlag [11], MOSS [12], YAP [13] and PDE4Java [14] are plagiarism detection systems for students’ programming submissions.
Different approaches have been adopted to develop APAG systems. Approaches can be categorized to three basic categories; dynamic or test based, semantic-similarity based, and graph based.
The dynamic-based is the most well known approach that has been used by many existing systems. Douce et al. reviewed automatic programming assessments which are dynamic-based in [15]. Using this approach, the mark assigned to a programming assignment depends on the output results from testing it against a predefined set of data. However, this approach is not applicable if a programming assignment does not compile and run to produce an output. In this case, no matter how the assignment is good it will receive a zero mark. Moreover, using dynamic-based approach does not ensure that the assignment producing correct output is following the required criteria. Examples of dynamic-based systems are Kassandra [16] and RoboProf [17,18].
The semantic similarity-based (SS-APAG) approach overcomes the drawbacks of the dynamic-based approach. Using this approach the grading of a student’s program is achieved by calculating semantic similarities between the student’s program and each correct model program after they are standardized. This approach evaluates how close a student’s source code to a correct solution? However, this approach can become expensive in terms of time and memory requirements if the program size and problem complexity increase. ELP [19] and SSBG [20] are two examples of this approach.
The graph based approach is a promising one which overcomes the drawbacks of other approaches. This approach represents source code as a graph with edges representing dependencies between different components of the program. Graph representation provides abstract information that is not only supports comparing source codes with lower cost (than semantic similarity approach) but also enables assessing source code quality through analyzing software metrics. Comparing graph representations for two programs is done on the structure level of the program. This approach has been applied in two different ways: graph transformation such as in [21] and graph similarity such as in [22].
3. Methodology
eGrader can efficiently and accurately grade a Java source code using both dynamic and static analysis. The dynamic analysis process is carried out using the JUnit framework [23] which has been proved to be effective, complete and precise. It provides features that do not only ease the dynamic analysis process but also makes it flexible to generate dynamic tests for different types of problems in several ways.
The static analysis process consists of two parts: the structural-similarity which is based on the graph representation of the program and the quality which is measured by software metrics. The graph representation is based on the Control Dependence Graphs (CDG) and Method Call Dependencies (MCD) which are constructed from the abstract syntax tree of the source code. From the graph representation, structure and software metrics are specified along with control structures’ positions and represented as a code which we call Identification Pattern. The identification patterns for models’ solutions are generated in Phase I (creating grading session) as depicted in Figure 1(a). The identification patterns for students’ submissions are produced in Phase II (grading students’ submissions phase) as depicted in Figure 1(b). The result of the static analysis is the outcome of the matching process between students’ identification patterns and models’ identification patterns as shown in Phase III of Figure 1(a).
3.1. Identification Pattern
The identification pattern is a representation of the structure and software engineering metrics of a program. The structure is presented in the identification pattern based on the code tracing (without executing it) starting from the main() method. The structure and software engineering metrics are two major components of any identification pattern. Example of identification pattern is shown in Figure 2.
3.1.1. The Structure Component
The structure component consists of several sub components represented with a mask of digits. Each sub-component represents a control structure or a method call in the program structure. Each sub-component is composed of three types of coding: basic category, control and position.
Table 1 shows the code representation for basic categories and controls of the structure components. For example, a for loop control is of the Loops basic category and for_loop control which is represented with the code 21. The code 1* is a representation for the Conditions basic category and General_statement control structure, which means any of the Conditions statements is accept-
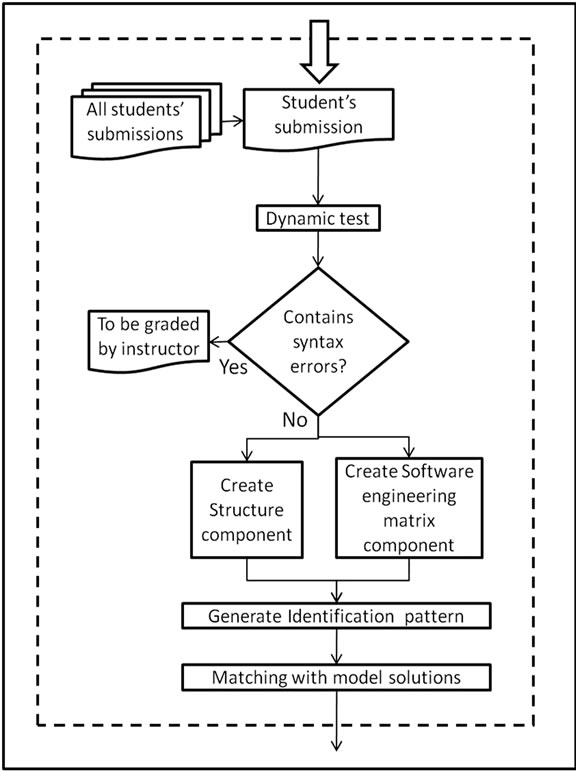
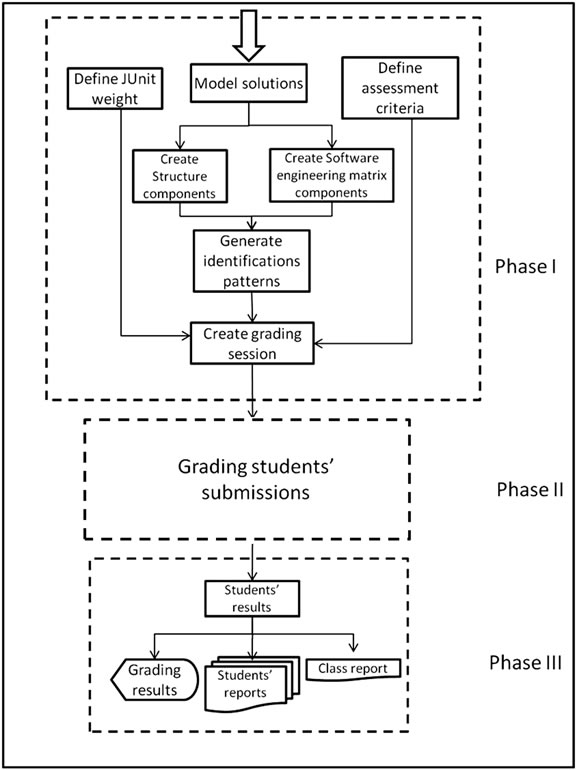
Figure 1. (a) The 3 phases of block diagram of eGrader; (b) Phase II of eGrader’s block diagram.

Figure 2. Example of an identification pattern.
able. This type of coding (wild character) is used in the model solution’s programs only.
The position code consists of one or more digits representing the position of a control structure or a method call in the whole program structure. It also represents the position relative to other control structures and method calls in the program structure.
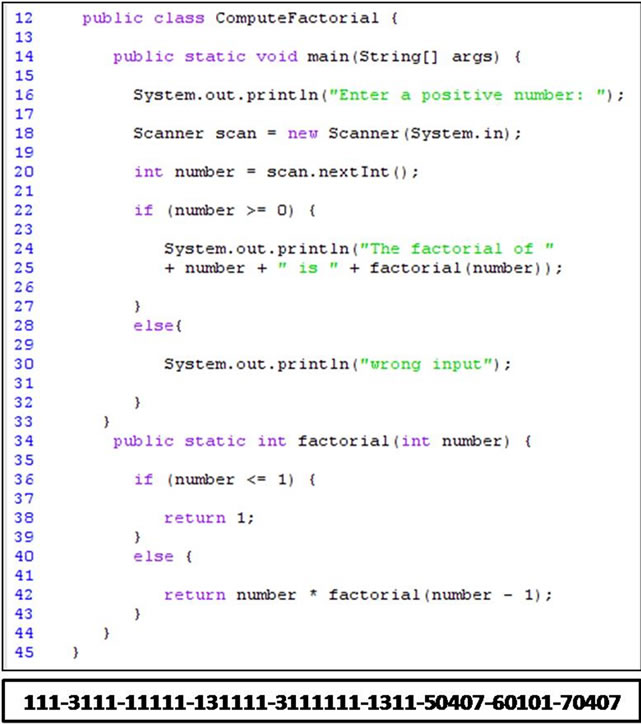
Figure 3 depicts an example of the structure component for the identification pattern Compute Factorial. Class Compute Factorial calls the method factorial to compute the factorial value after checking its validity (number ≥ 0). To trace Compute Factorial, we start with the control structure at line 24 (if (number ≥ 0)). Since this control structure is a condition control of type if_statement, the basic category is set to 1 and the control is set to 1 too if_statement. The position of this control structure is 1 as it is the first control structure to trace. The second control structure to trace is the method call at line 26 (fact = factorial (number)) which is a call to a non
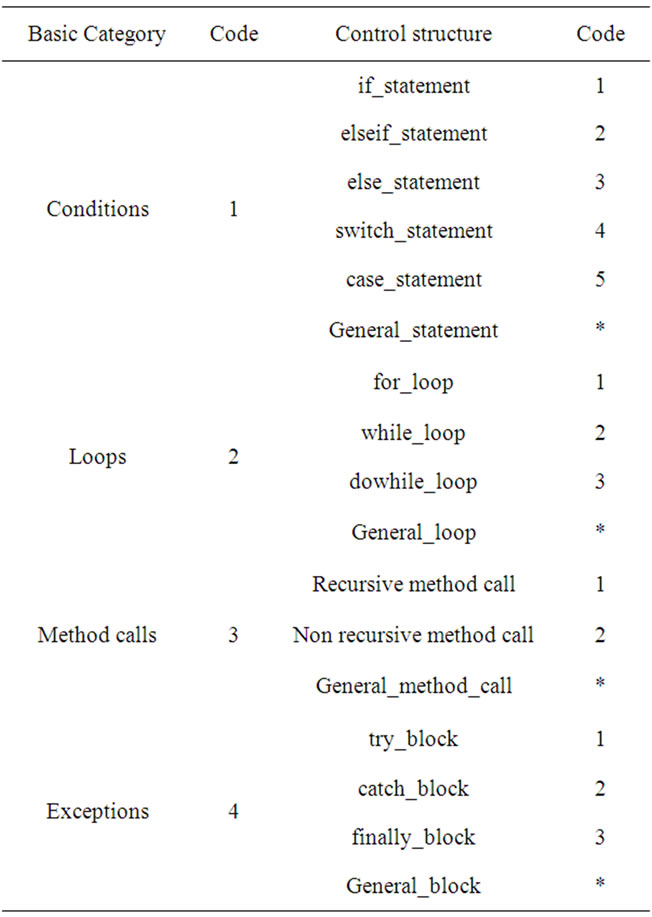
Table 1. The basic Categories and Controls of the structure component of the identification pattern.

Figure 3. Compute Factorial class.
recursive method. Based on Table 1, the basic category for the method call is 3 and a non recursive method has the control code 2. Since fact = factorial(number) is control dependent on the first control structure to trace, which is if (number ≥ 0), the number of digits in the position code will increase by one and will be 11. The at line 38 inside the method factorial has the code 11111, where the first 1 is for the basic category (conditions), the second 1 is for the control (if_statement) and the remaining 111 is for the position because it is dependent on statement in line 15. The control structure while (number > 0) at line 41 is traced after the control structure at line 38, so while (number > 0) has a position value greater than the position value of if (number ≥ 0) by one which is 112. The else_statement at line 29 is the last control structure to trace and it is control dependent on if (number ≥ 0). The code for the else part is 1311, where 1 is for the basic category, 3 for the control, and 11 is for the position. The whole ordered structure component of ComputeFactorial’s identification pattern is shown in Figure 4.
3.1.2. Software Engineering Metrics (SEM) Component
Software Engineering Metrics (SEM) consist of 3 subcomponents: number of variables, number of classes and number of built-in method calls. Each sub component consists of two or three parts depending on whether the SEM component is for a student’s program or a model program.
For a student’s program, each sub-component consists of two parts: Basic category and Number. The basic category codes are 5 for Variables, 6 for Classes, and 7 for Library method calls. The Number represents the number of each SEM component in the student’s program.
For the model program, each sub-component consists of three parts: The Basic category, MinNumber and MaxNumber. The basic category coding follows the same strategy as for the student’s program. Parameters MinNumber and MaxNumber consist of two digits each representing the minimum and the maximum number of SEM sub-component allowed, respectively.
Figure 5 shows examples of SEM component for identification patterns. An example of a SEM component for Compute Factorial (Figure 3) as a student’s program is shown in Figure 5(a). The basic category of type Variables has a number set to 07 which means the student use 7 variables in his/her program. The code 601 means there is one class in the file. The number of built-in method calls in the student’s program is 04 which is represented in the code 704, where 7 indicates the basic category (type library method calls). An example of a SEM component for Compute Factorial of Figure 3 as a model program is shown in Figure 5(b). The basic category of type Variables has a MinNumber equals to 04 and MaxNumber equals to 07 meaning that students are allowed to use a minimum of 4 variables and a maximum of 7 variables. Students should not use more than one class which is represented by the code 60101. The code 70410 indicates that students are allowed to use a minimum of 4 library method calls and no more than 10, where 7 represents the basic category of type library method calls.
3.1.3. Structure and SEM Analysis
The main idea behind the identification pattern is to analyze both the structure and the SEM of students’ programs. Therefore, an efficient strategy to compare identification patterns is required. Certain criteria need to be met to develop an efficient strategy to compare identification patterns. The criteria are as follows:
1) Identification pattern matching is based on the distance between them. The distance measure is defined as the number of missing control structures and SEM components from the model program in addition to the num-

Figure 4. Structure component of the Compute Factorial class.
 (a)
(a) (b)
(b)
Figure 5. (a) A student’s SEM component of Figure 3; (b) A model’s SEM component of Figure 3.
ber of extra control structures and SEM component in the student’s identification pattern. Formally, it is:
 (1)
(1)
where D is the distance, NMissing is the number of missing control structures, and NExtra is the number of extra control structures.
2) If there exists a model identification pattern that matches exactly a student’s identification pattern, the distance between both is set to zero.
3) If no exact match found, the best match is the model’s identification pattern which has the minimum distance D from the student’s identification pattern.
4) If two models’ identification patterns have the same distance from the student’s identification pattern, the best match is the one that maximizes the scored mark.
To illustrate our comparison process, an example for calculating factorial is presented. This example consists of two models’ solutions and one student’s solution. The first model solution calculates factorial using a recursive method (Figure 6(a)). The second one is a nonrecursive solution. An example of a student’s solution is shown in Figure 6(b).
The student’s identification pattern is compared with the first model identification pattern in Figure 7. The basic category and control of each control structure in the student’s identification pattern is compared with the basic category and control of each control structure in the model’s identification pattern until a match is found. The distance D in this example is equal to 2, as two control structures are missing; if_statement and elseif_statement.
The student’s identification pattern is compared also with the model’s identification pattern for a nonrecursive solution. The result of this comparison is as follows: 2 extra control structures, 2 missing control structures and 1 missing SEM. Therefore, the distance D is equal to 5.
As a result, the first model’s identification pattern better matches student’s identification pattern. The mark is to be assigned based on the first model program.
4. eGrader Framework
The framework of eGrader consists of three components: Grading Session Generator, Source code Grader, and Reports Generator. eGrader basic screen is shown in Figure 8.
4.1. Grading Session Generator
eGrader supports both generating and saving grading sessions. Generating a grading session is easy, flexible and quick. A grading session is generated through three steps: creating model list, creating assessment criteria, and creating new grading session.
 (a)
(a)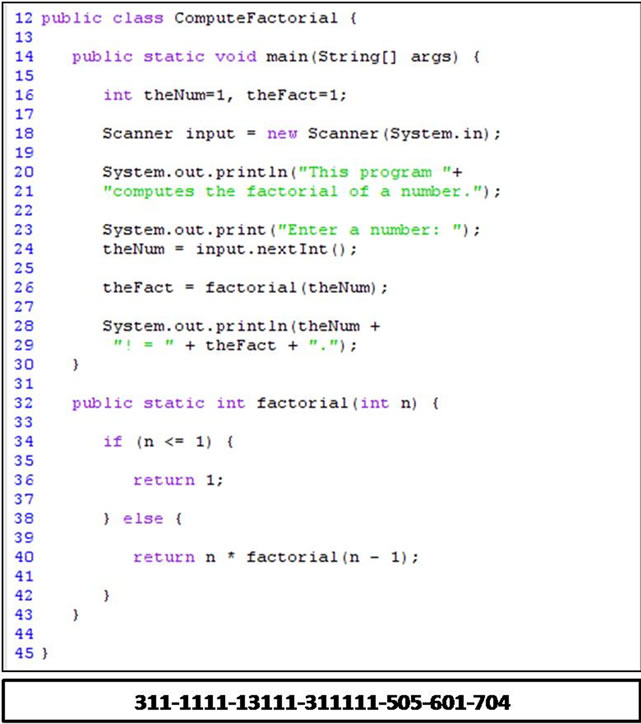 (b)
(b)
Figure 6. (a) Recursive solution-model answer; (b) A student’s solution.
4.1.1. Creating Model List
This is done simply by adding model solutions, where identification patterns are generated automatically. Each identification pattern represents the structure of its model solution. Once an identification pattern is generated, a

Figure 7. Comparison process between the student’s solution in Figure 6(b) and the model solution in Figure 6(a).
dialog box appears showing the identification pattern and providing a possibility to modify it (Figure 9). The modification options are: to choose another form of Java control structures or a general form. For example, if the identification pattern contains a for-loop structure which is represented in Figure 9 by 211, the available options are: to keep it, choose while-loop or do-while-loop instead, or choose the wild character (*) which represents any loop control. Software metrics are optional. Such metrics include number of variables, number of library methods and number of classes used. Adding each of the software metrics along with their values to the identification pattern is optional as shown in Figure 10. The model identification code is then added to the list. Model solution list can be saved and modified in future.
4.1.2. Assessment Criteria
In order to create and assessment scheme, assessment criteria are categorized into five categories:
1) Condition statements.
2) Loop statements.
3) Recursive & Nonrecursive method calls.
4) Exceptions.
5) Variables, classes, and library method calls.
Figure 11 shows the Assessment Criteria frame. Each category provides input fields for measuring category weight and penalty (except for category E) for extra controls. A category is added to grading process if it has a weight greater than zero. If the penalty value for a category is greater than zero, a student who uses extra controls (more than what is required in the program) of that category will be penalized. Weights and penalty values are normalized. Options in each category’s check list covers all the controls in an introductory Java course. Assessment criteria may be saved for future use.
4.1.3. Creating New Grading Session
A grading session is created through New grading session dialog. In this dialog three files need to be added which are the solutions set file, the assessment criteria file and the JUnit test file with an option for specifying the weight (which has to be in the range of [0,1]) for dynamic analysis phase as shown in Figure 12. Other files can be included such as data files to run or test students’ submissions. Once the grading session for a problem is generated, the grading process can take place.
4.2. Source Code Grader
As most of the existing systems do, the submitted source code need to be a zipped file named with the student’s identification number. This naming and submitting strategy is chosen in order not to burden the instructor with both searching for required files in different folders and keeping track of which submissions belong to which student. The grading process steps are as follows:
1) Loading grading session. List of solutions, folders and identification patterns are loaded into in a table form in the main eGrader’s frame.
2) Loading the submitted zipped files by specifying their folder.
3) Submissions will be graded and their output will be inserted into another table.
At this stage, the grading process is completed. The list of students’ names along with their details is in Excel
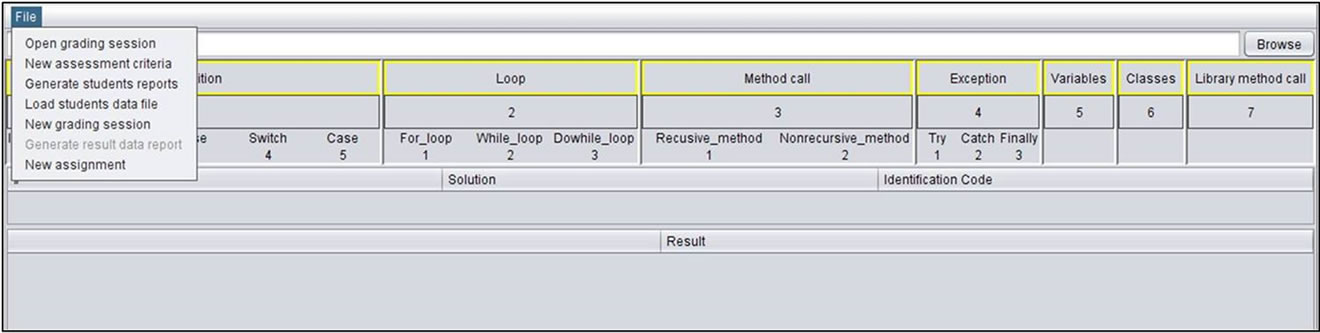
Figure 8. eGrader basic initial screen.
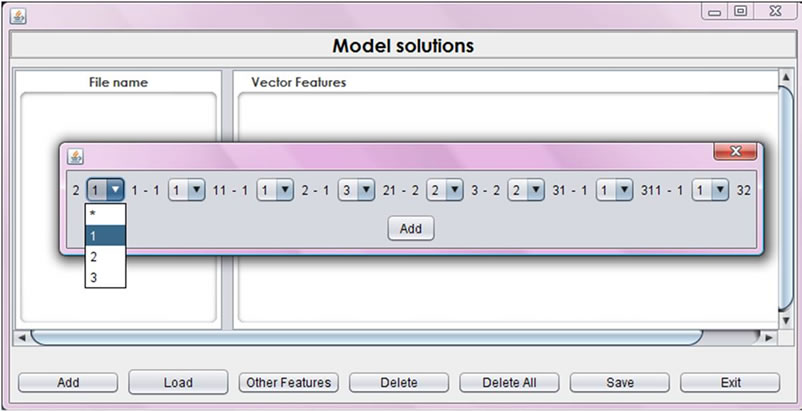
Figure 9. Identification code options in the Model solutions dialog box.
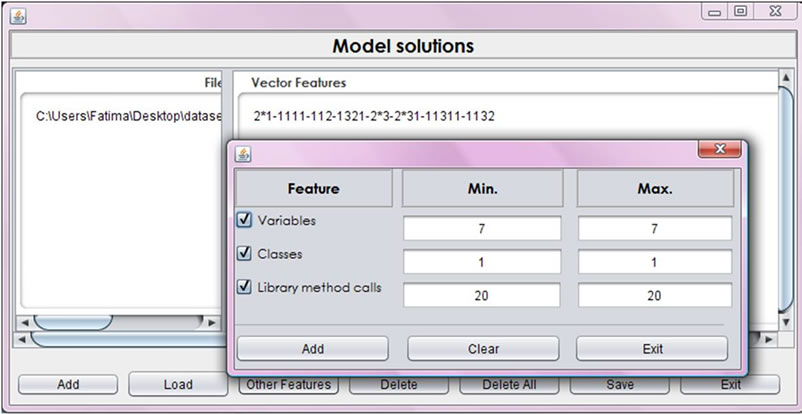
Figure 10. Software metrics in the Model solutions dialog box.
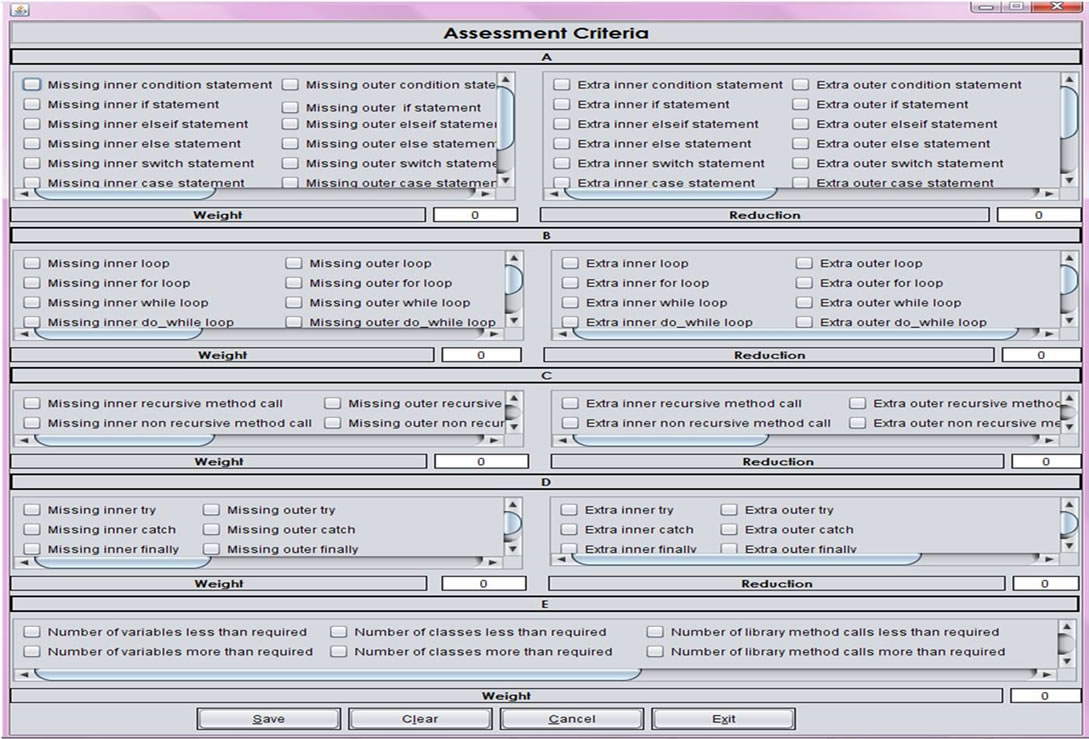
Figure 11. Assessment Criteria dialog box.
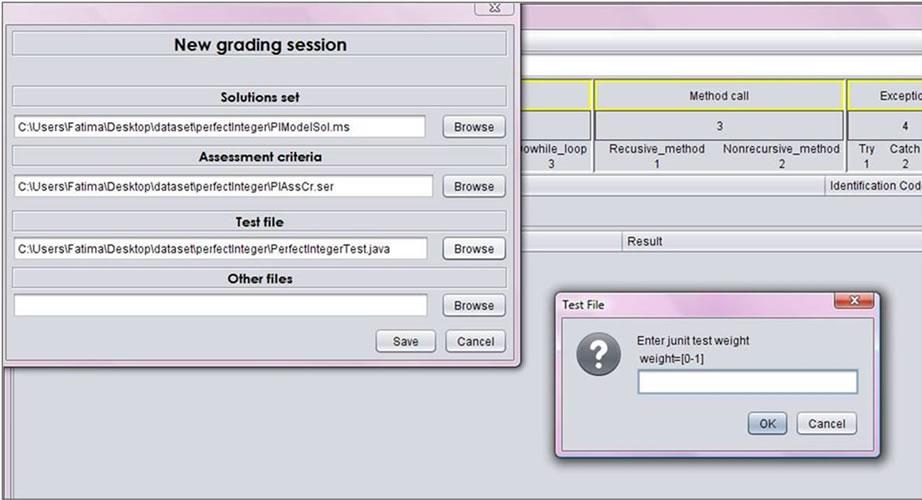
Figure 12. A new grading session.
file that is to be loaded to eGrader.
Marking starts by running the source code using the JUnit class (dynamic test). If the dynamic test is successful, the system proceeds to the static test. Otherwise, a report is generated indicating that this submission needs to be checked by the instructor.
4.3. Reports Generator
eGrader not only grades Java code effectively but also provides the instructor with detailed information about the grading process. It helps to analyze students’ understanding of basic programming concepts. There are two types of reports that are produced by eGrader: students’ assessment reports and class reports.
4.3.1. Students Assessment Reports
After the grading process is completed and the student data file (an excel file includes student names and identification numbers) is loaded, students’ reports are generated. Such reports consist of four different sections:
1) Identification: contains student information such as name, identification number, the result of grading his/her submission. Figure 13 shows an example for Compute Factorial assignment.
2) Marking: shows the details of the marking scheme after conducting both the dynamic and static tests. The dynamic test result includes the total number of tests and the number of tests that failed. The static part shows the 5 general categories and the mark for each one, if required. In the case of encountering errors, a message will be inserted to indicate the source of the error. Marks are deducted based on the original marking scheme set by the instructor/grader. Example is shown in Figure 13.
3) Model solution: points to the model solution that best matches student’s submission. Example is shown in Figure 14(a).
4) Original code: shows students’ solution. A matching between the structure of the model solution and the structure of the student’s submission is displayed using color matching between corresponding control structures. Example is shown in Figure 14(b).
A report for a student’s submission that contains syntax errors consists of one part only, which indicates that the submission has syntax errors and to be checked by a grader. The total mark for this submission is zero.
4.3.2. Class Reports
A class report is a summary report on the whole class performance on a specific assignment. This report consists of three parts (three excel sheets) which are: statistics, dynamic test details and static test details.
Useful information such as the assignment’s difficulty level, the number of students who managed to submit a solution, and the most and least common solutions, are summarized in the statistics part. As presented in Figure 15, the statistics part contains the following data:
• Number of students’ submissions for a given assignment based on the number of graded submissions;
• Number of model solutions;
• Most popular model solution;
• Least popular model solution;
• Number of unit tests used to test each submission;
• Number of submissions failed all unit tests. This number indicates the submissions that failed all the tests in the JUnit test class;
• Number of failed submissions because of syntax errors.
The dynamic test details part provides a general overview of the performance of the class. This part is shown in Figure 16. It displays the following data:
• Tests failed to run by a student’s submission along with the number of students who failed each test;
• List of runtime errors. Such information is useful for
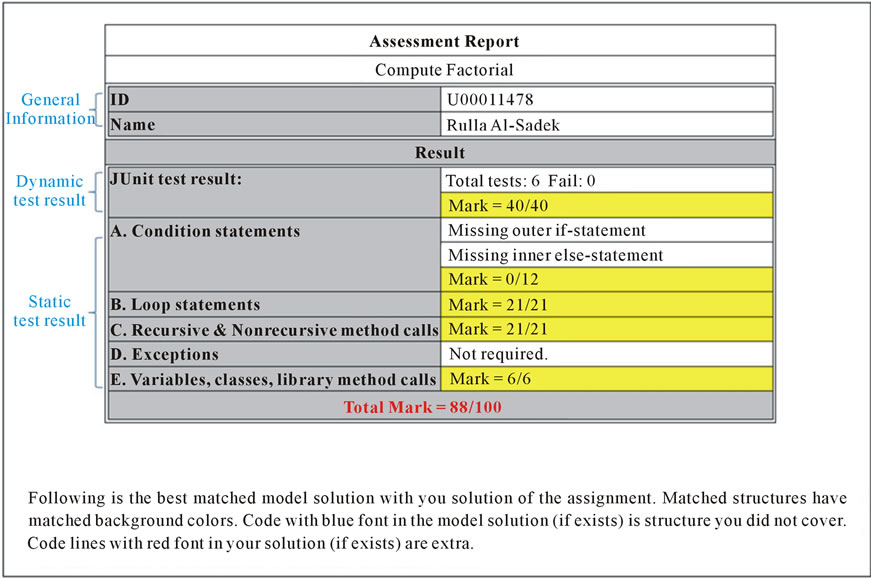
Figure 13. Result (part one) of a student’s report for the Compute Factorial assignment.
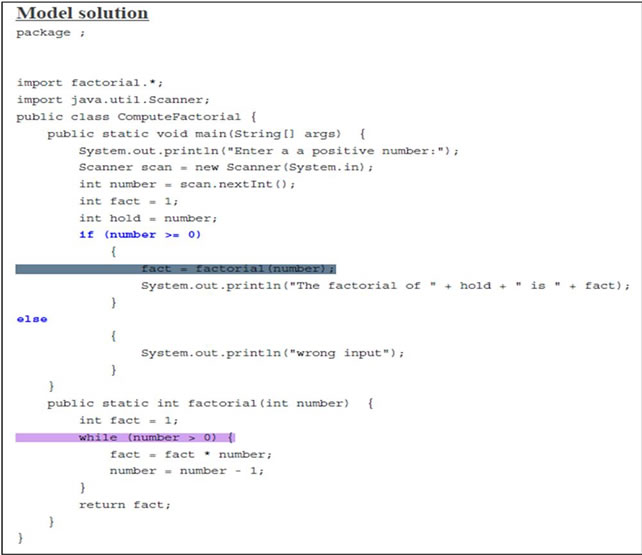 (a)
(a)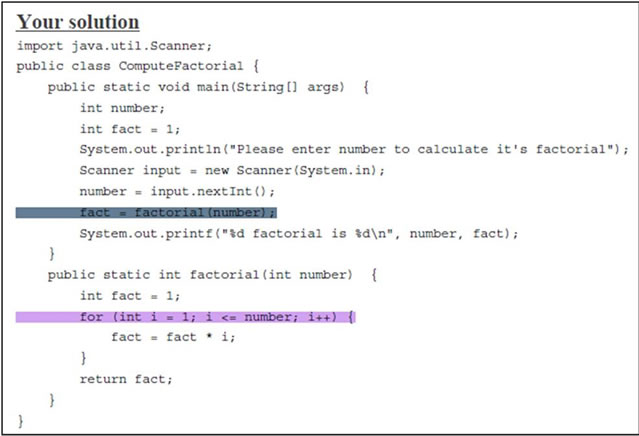 (b)
(b)
Figure 14. (a) Model solution (part two) of a student’s assessment report; (b) The student’s solution (part three) of a student’s assessment report.
the instructor to identify common problems and as a result provide necessary clarification of some concepts in class;
• Other useful statistics such as average, maximum and minimum marks.
Static test details part provides information on the performance of the class in the general five categories. This part consists of the following data:
• Assignment Requirements which contains five categories, where each has three measures: average mark, highest mark and lowest mark, if the category is required. Otherwise, the category will be reported as not required. Group A. Condition statements; for example, is represented by, the average mark which is the average of all submissions marks for this group, the highest mark which is the highest submission’s mark for this group and the lowest mark which is the lowest submission’s mark for this group. The same applies for all the other categories;
• Other useful statistics such as average, maximum and minimum marks.
5. Experimental Results
eGrader has been evaluated by a representative data set of students’ solution in Java introductory programming courses at the University of Sharjah. This data set consists of students’ submissions for two semesters with a total of 191 submissions with an average of 24 students in each class. The assignment set covers 9 different problems.
Four types of programming assignments were used, which are:
• Assignment 1: tests the ability to use variables, input statements, Java expressions and mathematical com-

Figure 15. Statistics part of the Compute Factorial assignment report.
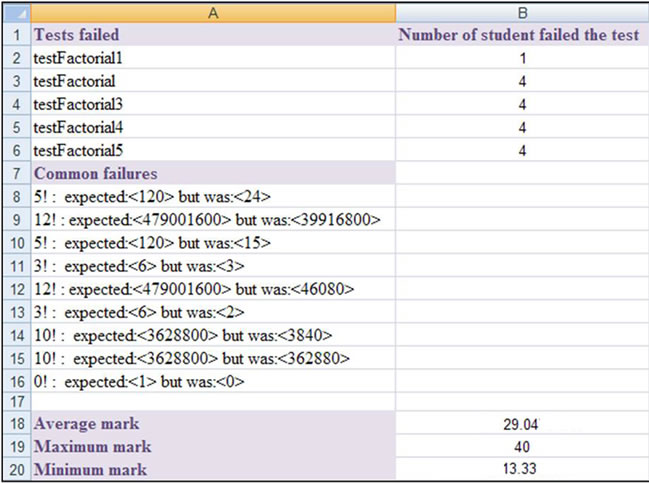
Figure 16. Dynamic test details part of the Compute Factorial assignment report.
putations and output statements;
• Assignment 2: tests the ability to use condition control structures such as if/else-if/else and switch statement. It also tests students’ abilities to use loop structures such as for, while and do-while statements;
• Assignment 3: tests the ability to use recursive and non recursive methods;
• Assignment 4: tests the ability to use arrays.
We are using four performance measures to evaluate eGrader performance. Namely, sensitivity, specificity, precision and accuracy.
Sensitivity measures how many of the correct submissions are in fact rewarded. Whereas the specificity is a measure of how many of the wrong submissions are penalized? Precision is a measure how many of the rewarded submissions are correct? Finally, accuracy is a measure of the number of correctly classified submissions.
Evaluation shows a high success rate represented by the performance measures which are sensitivity (97.37%), specificity (98.1%), precision (98.04%) and accuracy (97.07%) as depicted in Figure 17.
6. Conclusion and Future Work
eGrader is a graph based grading system for Java introductory programming courses. It grades submissions both statically and dynamically to ensure a complete and
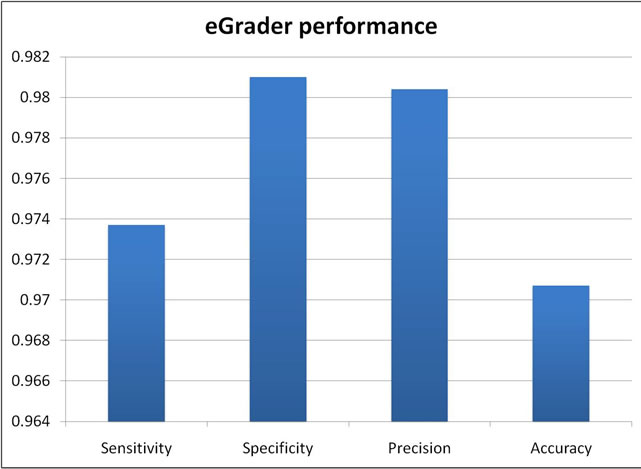
Figure 17. eGrader performance evaluation.
through testing. Dynamic analysis in our approach is based on the JUnit framework which has been proved to be effective, complete and precise. This makes it a suitable tool for the problem of dynamic analysis for students’ programs. The static analysis process consists of two parts: the structure-similarity which is based on the graph representation of the program and the quality which is measured by software metrics. The graph representation is based on the Control Dependence Graphs (CDG) and Method Call Dependencies (MCD) which are constructed from the abstract syntax tree of the source code. From the graph representation, structure and software metrics are specified along with control structures' positions and represented as a code which we call it Identification Pattern.
eGrader outperformed other systems in two ways. It can efficiently and accurately grade submissions with semantic error. It also generates a detailed feedback for each student and a report for the overall performance for each assignment. This makes eGrader not only an efficient grading system but also a data mining tool to analyze students’ performance.
eGrader was appraised by instructors and teaching assistants for its overall performance (97.6%) and the great reduction in time needed for grading submissions when using it. Their comments provided useful feedback for improvement.
eGrader can be extended to incorporate other features such as: Support GUI-based programs, grade assignments in other programming languages and offer the eGrader online.
REFERENCES
- J. Hollingsworth, “Automatic Graders for Programming Classes,” Communications of the ACM, Vol. 3, No. 10, 1960, pp. 528-529. doi:10.1145/367415.367422
- A. Elnagar and L. Lulu, “A Visual Tool for Computer Supported Learning: The Robot Motion Planning Example,” International Journal of Computers & Education, Vol. 49, No. 2, 2007, pp. 269-283.
- M. W. Goldberg, “Calos: An Experiment with ComputerAided Learning for Operating Systems,” ACM SIGCSE Bulletin, Vol. 28, No. 1, 1996, pp. 175-179. doi:10.1145/236462.236534
- S. Harous and A. Benmerzouga, “A Computer Aided Learning Tool,” Journal of Computer Science, Vol. 4, No. 1, 2008, pp. 10-14. doi:10.3844/jcssp.2008.10.14
- B. W. Becker, “Teaching CS1 with Karel the Robot in JAVA,” ACM SIGCSE Bulletin, Vol. 33, No. 1, 2001, pp. 50-54. doi:10.1145/366413.364536
- C. Kelleher, “Alice: Using 3d Gaming Technology to Draw Students into Computer Science,” Proceedings of the 4th Game Design and Technology Workshop and Conference, Liverpool, 2006, pp. 16-20.
- C. Evans, “The Effectiveness of m-Learning in the Form of Podcast Revision Lectures in Higher Education,” International Journal of Computers & Education, Vol. 50, No. 2, 2008, pp. 491-498.
- L. F. Motiwalla, “Mobile Learning: A Framework and Evaluation,” International Journal of Computers & Education, Vol. 49, No. 3, 2007, pp. 581-596.
- C. Vibet, “Handling Quiz-Based Tests with TEX Macros,” Education and Information Technologies, Vol. 2, No. 3, 1997, pp. 235-246. doi:10.1023/A:1018669415152
- D. Andrews, B. Nonnecke and J. Preece, “Electronic Survey Methodology: A Case Study in Reaching Hard-toInvolve Internet Users,” International Journal of HumanComputer Interaction, Vol. 16, No. 2, 2003, pp. 185-210. doi:10.1207/S15327590IJHC1602_04
- L. Prechelt, G. Malpohl and M. Philippsen, “Finding plagiarism Among a Set of Programs with JPlag,” Journal of Universal Computer Science, Vol. 8, No. 11, 2002, pp. 1016-1038.
- A. Aiken, “Moss: A System for Detecting Software Plagiarism. http://www.cs.stanford.edu/aiken/moss.html
- M. J. Wise, “YAP3: Improved Detection of Similarities in Computer Program and Other Texts,” ACM SIGCSE, Vol. 28, No. 1, 1996, pp. 130-134. doi:10.1145/236462.236525
- J. Jadalla and A. Elnagar, “PDE4Java: Plagiarism Detection Engine for Java Source Code: A Clustering Approach,” International Journal of Business Intelligence and Data Mining, Vol. 3, No. 2, 2008, pp. 121-135. doi:10.1504/IJBIDM.2008.020514
- C. Douce, D. Livingstone and J. Orwell, “Automatic TestBased Assessment of Programming: A Review,” Journal on Educational Resources in Computing, Vol. 5, No. 3, 2005, p. 4. doi:10.1145/1163405.1163409
- U. Von Matt, “Kassandra: The Automatic Grading System,” SIGCUE Outlook, Vol. 22, No. 1, 1994, pp. 26-40. doi:10.1145/182107.182101
- C. Daly, “RoboProf and an Introductory Computer Programming Course,” ACM SIGCSE Bulletin, Vol. 31, No. 3, 1999, pp. 155-158. doi:10.1145/384267.305904
- C. Daly and J. Waldron, “Assessing the Assessment of Programming Ability,” Proceedings of the 35th SIGCSE technical Symposium on Computer Science Education, Norfolk, 3-7 March 2004, pp. 210-213.
- N. Truong, P. Bancroft and P. Roe, “ELP-A Web Environment for Learning to Program,” Proceeding of the 19th Annual Conference of the Australasian Society for Computers in Learning in Tertiary Education, Vol. 19, Auckland, 8-11 December 2002, pp. 661-670.
- T. Wang, X. Su, Y. Wang and P. Ma,” Semantic Similarity-Based Grading of Student Programs,” Information and Software Technology, Vol. 49, No. 2, 2007, pp. 99-107. doi:10.1016/j.infsof.2006.03.001
- N. Truong, P. Roe and P. Bancroft, “Static Analysis of Students’ Java Programs,” Proceedings of the 6th Conference on Australasian Computing Education, Vol. 30, 2004, p. 325.
- K. A. Naude, J. H. Greyling and D. Vogts, “Marking Student Programs Using Graph Similarity,” Computers & Education, Vol. 54, No. 2, 2010, pp. 545-561. doi:10.1016/j.compedu.2009.09.005
- V. Massol and T. Husted, “JUnit in Action,” Manning Publications Co., Greenwich, 2003.

