Journal of Water Resource and Protection
Vol.09 No.08(2017), Article ID:77399,15 pages
10.4236/jwarp.2017.98063
Comparative Evaluation of Spatial Interpolation Methods for Estimation of Missing Meteorological Variables over Ethiopia
Andualem Shigute Boke
Department of Hydraulic and Water Resources Engineering, Jimma Institute of Technology, Jimma University, Jimma, Ethiopia

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 20, 2017; Accepted: July 1, 2017; Published: July 4, 2017
ABSTRACT
In developing countries like Ethiopia where there is abundant water resources potential and also luck of reliable meteorological quality data, it expected to face the problem of missing meteorological data. Therefore, in conducting any water resources studies in any river basin for water resource project planning and management (like small scale irrigation), the first step before starting data analysis is to fill up the missing values of the meteorological variables (like rainfall, temperature, sunshine, wind speed etc.) which are required to start the study. One way of filling these missing variables is using datasets from other stations in the surrounding and applying appropriate spatial interpolation methods. A lot of studies have been conducted around the world to identify which method is the best to be applied to particular study area among the available spatial interpolation techniques. But when we come to Ethiopia, the study area, few or no studies are conducted to recommend the best performed method. Therefore, the objective of this paper is to conduct comparative evaluation of five interpolation techniques Nearest Neighbour (NN), Inverse Distance Weighting Average (IDWA), Modified Inverse Distance Weighting Average (MIDWA), Kriging Method (KM) and Thin Plate Spline (TPS) for estimation of four climatic variables (rainfall, mean temperature, wind speed and sunshine fraction) over complex topography of Ethiopia. Performance assessment is done using Mean Error (ME), Mean Absolute Error (MAE), Mean Relative Error (MRE) and Root Mean Square Error (RMSE); and the number of the meteorological stations selected for validation is ten (10) and these are distributed over the study area taking into account the variation of elevation ranging from 860 m (Awash) to 2420 m (Debremarkos) above sea level. The radial distances of 100 km and 200 km were selected and it was found that 100 km radial distance was not appropriate to compare all methods as some variables could not be estimated by KM and TPS. Therefore, 200 km was selected for further analysis and the result showed that NN, IDWA, and MIDWA were best methods relative to the remaining two methods (KM and TPS) for all variables and all stations except at Dire Dawa and Addis Ababa-Bole for estimation of wind speed using all methods except NN, and rainfall using TPS, respectively. Hence, NN, IDWA, and MIDWA methods could be used for estimation of missing meteorological variables over Ethiopia whenever necessary.
Keywords:
Spatial Interpolation, Meteorological Variables, Comparative Evaluation, Ethiopia

1. Introduction
In developing countries like Ethiopia where there is sufficient amount of water resources potential and also luck of high quality meteorological data, it expected to have the problem of facing missing meteorological data even though all means were used to avoid these missing values from the records [1] [2] . Some of the causes of the occurrence of these data problem could be absence of observer, malfunction of instruments, incorrect measurements, relocation of stations, and loss of records [3] [4] .
During conducting any hydrological and environmental studies/modeling in any river basin for water resources project planning and management, the first step before starting data analysis is to fill up the missing values of the meteorological variables (like rainfall, temperature, sunshine, wind speed etc.) required for the study [5] . Unless these missing values are filled up by appropriate methods so as to make the dataset complete, the data used may be biased and can lead to wrong conclusions [6] . One way of filling these missing meteorological variables at targeted station is using datasets from other selected stations in the surrounding and applying appropriate spatial interpolation methods [7] . There are more than 42 interpolation methods available in the literature [8] . In order to get good results of estimation, it is a must to select best interpolation technique for the study selected as the interpolation techniques are affected by different factors like sample size of the data, the sampling design and data properties [8] .
At global scale [9] used Thin-Plate Spline method as interpolation technique to generate global (excluding Antarctica) monthly data for precipitation, and mean, minimum and maximum temperature using data collected from different sources in the period 1950-2000.
Another study by [10] carried out over England and Wales using four interpolation methods (Partial Thin Plate Splines, Ordinary Kriging, Trend Surface and Inverse Distance Weighting Method) for daily maximum and daily minimum temperature of 1976; and found that Partial Thin Plate Splines performed best whereas Trend Surface was the poorest.
[11] conducted a comparative study on four interpolation methods (Ordinary Kriging, Inverse Distance Squared, Gradient-Plus-Inverse-Distance Squared and Residual Kriging) for predicting reference evapotranspiration over Greece territory and found that Gradient-Plus-Inverse-Distance Squared performed best and the result from Residual Kriging is not optimal even though it performed better than Inverse Distance Squared and Ordinary Kriging. The evaluation statistics used are the mean error, mean absolute error and root mean squared error.
A study carried out by [12] over South Africa to evaluate performance of four spatial interpolation methods (Inverse Distance Weighting, Ordinary Kriging, Univariate Kriging and Co Kriging) using annual rainfall collected from 545 stations and the result showed that Ordinary Kriging performed best compared to other three methods.
[13] developed multiple regression models for generating mean annual rainfall as a function of elevation and geographic location for 63 Ethiopian meteorological stations using datasets from 1969 up to 1985. In this study, regionalization is the main technique applied to generate mean annual rainfall.
[14] evaluated four spatial interpolation techniques (Arithmetic Mean, AM; Normal Ratio, NR; Inverse Distance Weighting, IDW and Coefficient of Correlation Weighting, CCW) for filling missing daily rainfall over upper Blue Nile river particularly on Gumera watershed using daily rainfall data (1987-2008) collected from nine stations and found that AM and CCW methods had shown better performance. On the lowland plain and near to Lake Tana it is AM while upstream and on the mountainous areas it is CCW that showed better performance where as NR is not good method to this area.
When we come to the selected study area, Ethiopia, very little studies are conducted on the selection of spatial interpolation techniques for estimating missing variables which could be used as input to some hydrological and other water related models. Before selecting among the available interpolation techniques, it is important to properly test their performance over the selected study so as to get best results relatively.
In areas where there is insufficient number of meteorological stations, it would be difficult to find continuously recorded meteorological datasets. In such cases there should be an alternative source of data to be used for water resources and environmental studies or modeling. One source of such data type is FAO database developed for the globe data collected by World Meteorological Service Agency; and New_LocClim_1.10 (Local Climate Estimator version 1.10) [15] is one of those databases. In this database there are nine spatial interpolation techniques available and nothing is known which one is best for which part of the world; hence the result obtained from one method will give different results as compared to the results that could be obtained from another method for the same station.
Therefore, the main objective of this paper is to comparatively evaluate most commonly used five spatial interpolation techniques and four meteorological variables found in FAO database (New_LocClim_1.10); and then to recommend the best performing interpolation methods to be used in Ethiopia.
2. Materials and Methods
2.1. Description of Study Area
The selected study area is Ethiopia located in East Africa. The country has very complex variation of topography and geology. The elevation of the area varies from 126 meters below sea level (Dalol depression) and 4620 meters above sea level (Mount Ras Dashen). The surface area of the country is 1.13 million square kilometers and 99.3% (land) and 0.7% is covered by water bodies (Lakes). This country is well known for its water resources potential. It has 12 major river basins and the amount of water resources available as surface run and ground water potential per year is estimated to be 122 BCM and 2.6 - 6.5 BCM, respectively [16] . The other important point is that there is very high spatial and temporal rainfall variation across the country which resulted in uneven distribution of the water resources of the country throughout the year. According to [17] the population of Ethiopia is 102,765,596 (19.8 % in urban and 80.2% in rural areas) by 2016. Study area map with selected base meteorological stations is given in Figure 1.
Figure 1. Study area map (Ethiopia) and spatial distribution of selected meteorological stations.
2.2. Data
Datasets used in this study area are taken from FAO database called Local Climate Estimator (or New_LocClim_1.10, as it is briefly explained in Introduction part of this paper) prepared for the globe based on data collected from meteorological stations around the world [15] . The datasets included in this tool are of two types (observed data in monthly scale; synthetic dataset in daily& monthly scale) eight (8) meteorological variables (rainfall, wind speed, mean temperature, maximum temperature, minimum temperature, vapor pressure, and sunshine fraction) both for observed and synthetic datasets; and both of the datasets are long-term average values. In the same tool, nine (9) interpolation methods were built in for generation of synthetic data.
Among the eight (8) variables found in the tool, only four (rainfall, mean temperature, wind speed, and sunshine fraction) commonly used variables were included in the study. The long-term average monthly observed dataset is given in Table 1 for selected 10 reference meteorological stations for validation [18] ; and the name and geographic locations of the selected meteorological stations are described in Table 2 and spatial distribution is shown in Figure 1.
During selection of the validation stations, an attempt has been made to include elevation ranges from 860 m (Awash) up to 2420 m (Debremarkos) so as to see the influence of topography on the accuracy of interpolators and their representativeness for the whole country. The same is true for the Longitude and Latitude. In Table 1, long year average values of observed meteorological data of the selected stations are shown.
2.3. Spatial Interpolation Methods
According to [8] , all interpolation techniques available in literature (more than 42) are classified in one of the following categories: i) Geostatistical ii) Non-
Table 1. Observed long-term average values of meteorological variables at selected validation stations.
Table 2. Name and geographic location of selected base meteorological stations.
Geostatistical or iii) combined. Based on the number of variables involved, Geostatistical categories could be univariate or multivariate. In the univariate type, only the primary variables are considered for interpolation whereas in case of the multivariate other secondary variables (such as elevation) are included. The algorithm used in all spatial interpolation methods is similar.
Based on the work of [8] , the general formulation used in all the available interpolation methods is similar and the formulation is as follows:
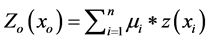 (1)
(1)
where:
Zo = estimated value of an attribute or variable at point of interest xo,
z = observed value at the sampled point (xi);
µ = weight assigned to the sampled point;
n = number of sampling points used for estimation;
xi = represents geographic coordinate (x, y) at location i.
Therefore, one interpolation is different from the other only by the methods used to estimate the weighting factor, µ. The theoretical background of each of the selected methods will be described one by one as in the coming subsections.
2.3.1. Nearest Neighbor (NN)
In this method of estimation sampling point nearest to the missing point are considering in such a way that perpendicular bisectors are drawn between sampling points so as to form polygons (like Thiessen polygon). Then each of the sampling points will have one polygon and the sampling point will be located at the center of the polygon. Points located in each of the polygons will have equal weight. If we designated these polygons by 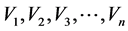 then weighting factors (μ) described in Section 2.3 are formulated as follows [8] :
then weighting factors (μ) described in Section 2.3 are formulated as follows [8] :
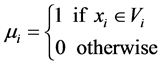 (2)
(2)
Therefore, for estimating missing meteorological variable at point of the interest this method will assign 1as a weight for sampling point located in the polygon and otherwise 0.
Then the general formulation remains the same as briefly explained in the Equation (1) above.
2.3.2. Inverse Distance Weighing Average (IDWA)
In this method estimation of missing value of meteorological variables at the point of interest is done by a linear combination of the weighted mean of measured variables at surrounding stations as inverse function of the distance of point of the interest from surrounding meteorological stations. The binding assumption in this method is that the closer the surrounding station to point of interest the more similar the corresponding meteorological variables will be and vice verse [8] .
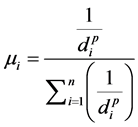 (3)
(3)
where:
di: distance between surrounding station and station where the variable is missing;
n: is the number of surrounding stations where the corresponding variable has measured value;
p: is power (influential parameter on IDWA factor and commonly 2);
µi: weighting factor assigned to each of the stations based on their distance from the point of Interest.
2.3.3. Modified Inverse Distance Weighing Average (MIDWA)
As the name implies Modified Inverse Distance Weighting Average (MIDWA) method is the modified form of IDWA method. The modification is done on the weighting factor by introducing the effect of elevation difference. If the elevation difference between the base station and the surrounding station is large, the effect of elevation difference will have an effect on estimated value of the meteorological variable. [19] replaced the weighting factor in the IDWA method by introducing the ratio of distance to elevation difference as follows and keeping the other factors similar to IDWA method. The same author mentioned that this relation is good to mountainous areas (like Ethiopia, study area). A little modification of symbols has been made to be consistent with IDWA method.
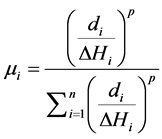 (4)
(4)
where:
di: distance between surrounding station and station where the variable is missing;
n: is the number of surrounding stations where the corresponding variable has measured value;
p: is power (influential parameter on IDWA factor and commonly 2);
DHi: the elevation difference between the base station and the surrounding stations;
µi: weighting factor assigned to each of the stations based on the ratio (di/DHi).
2.3.4. Kriging Method (KM)
The commonly used kriging method among the kriging families is ordinary kriging. In this estimation method, optimal and unbiased estimation of regionalized variables at unsampled location is carried out and the nature of the data at the sampled locations should be free of trend [11] . The general formulation developed in Equation (1) is applicable here also.
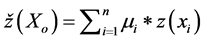 (5)
(5)
where:
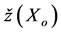 = estimated value of an attribute or variable at point of interest Xo,
= estimated value of an attribute or variable at point of interest Xo,
z = observed value at the sampled point (xi);
m = weight assignedto the sampled point;
n = number of sample points used for estimation;
xi = represents geographic coordinate (x, y) at location i.
The considerations taken in assigning weights in kriging are two:
1. The estimate, 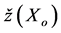 , of the true value, Z(X0), is unbiased:
, of the true value, Z(X0), is unbiased:
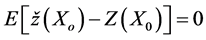
2. The prediction variance is minimum:
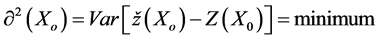
2.3.5. Thin-Plate-Spline (TPS)
To estimate missing values of any meteorological variable at base station, Thin- Plate-Spline method is one option among the available methods. As it is explained in [13] , the basic equation for Partial Spline method for n number of measurement stations for the variable of interest to be estimated at base station, say X0, represented by Zo is given as follows:-
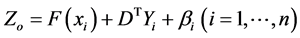 (6)
(6)
where:
Zo: predicted value of a missing meteorological variable at base station;
xi: is a d-dimensional vector of independent variable;
F: is an unknown smooth function of the xi;
Yi: is a p-dimensional vector of independent co-variates;
D: is an unknown p-dimensional vector of coefficient of the Yi;
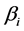 : is zero mean randomerror term.
: is zero mean randomerror term.
The above model is reduced to ordinary Thin-Plate-Spline (or Thin-Plate- Spline method) when the value of p is zero (or, p = 0), which means there is no covariance. Therefore, for this particular study Thin-Plate-Spline method is selected and this method is relatively robust and developed for climatic data [8] .
Summary of the selected methods for this study with their corresponding abbreviations is given below in Table 3.
2.4. Assumptions, Limitations and Suitability of Spatial Interpolation Methods
Each of the selected spatial interpolation methods has both merits and demerits; and Table 4 shows summary of these.
2.5. Evaluation of Spatial Interpolation Methods
In [8] [11] , different methods of spatial interpolation techniques were well reviewed but all of the studies could not reveal which method is the best method to be applied worldwide and for all discipline as the accuracy of the methods is affected by different factors rather than only on the interpolator itself. Therefore, it
Table 3. Spatial interpolation methods used for the study.
Table 4. Theoretical comparison of spatial interpolation methods: assumptions, limitations and suitability [8] [20] .
is important to select the appropriate interpolator for a specific study area before carrying out the interpolation process and one way of making this is an evaluation of each of the interpolation methods selected so as to identify which method is giving us the best estimates among the selected methods for our study. The commonly used way of evaluating performance of these interpolation techniques is using the concept of cross validation which can be expressed by commonly used statistical indicators [2] [11] [20] [21] [22] and they are described as follows:
1. Mean Error (ME): shows the degree of bias between the measured and predicted variable.
2. Mean Absolute Error (MAE): indicates the measure of how far is the predicted value from error regardless of the sign.
3. Mean Relative Error (MRE): provides how far the predicted value is from error relative to the measured value.
4. Root Mean Square Error (RMSE): Shows how sensitive is the predicted value towards outliers. The formula for each of the above mentioned statistical indicators are given below:
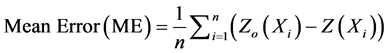 (7)
(7)



where:
n: is number of data points ( or stations) in consideration;
Zo: predicted value of a missing meteorological variable at base station;
Z: measured value of corresponding meteorological variable at base station;
Xi: is geographic coordinates (x, y) at station i.
3. Results and Discussion
3.1. Radius of Influence, r = 100 km
According to recommendation of [23] , as the first attempt, the radius of influence was specified as 100 km and some observation was made and the following results were obtained:
First, for common radial distance, r = 100 km ,the number of sampling stations selected for all variables, for all stations, and for all interpolation methods is the same and it is 10.
Second, for radial distance of 100 km some variables couldn’t be estimated due to lack of sufficient sampling stations (less than 10) around the selected validation station for some interpolation methods, particularly this radius of influence (r = 100 km) does not work for Kriging Method (KM) and Thin Plate Spline (TPS) nearly for all stations. With regard to variables, for the selected radius of influence it was not possible to get estimation values for rainfall at Debremarkos, Gondar, and Negele for KM and TPS. For all variables, it was impossible to predict values using KM for Awash station. For wind speed, KM is not good method nearly for all stations.
Third, the three methods (NN, IDWA, and MIDWA) have nearly similar performance and very close to the observed values for all variables at all stations; therefore, these methods could be used for estimating missing meteorological variables over the country Ethiopia whenever it is important.
Fourth, the analysis done for each of the considered station is not complete due to very limited number of stations with in 100 km radius for estimating some variables at selected stations. Therefore, another option was proposed to carry out complete and confidential analysis; and this is to increase the radius of influence from 100 km to 200 km, as there are similar studies conducted in another part of the world using radial distance more than 100 km [24] [25] [26] and conduct the analysis again so as to see if there is any change on the results.
3.2. Radius of Influence, r = 200 km
Even though the recommended radial distance for spatial interpolation is 100 km in most of the literature, it does not work effectively for this particularly identified study area due to complexity of the topography and sparse distribution of meteorological stations over the study area. Therefore, in order to have the chance to compare the performance of all five methods of estimation for all four variables for the stations in consideration, the radius of influence was increased from 100 km to 200 km; and the result was pretty good in giving prediction results for all four variables involving all five methods of prediction except rainfall at Addis Ababa-Bole station for the method TPS. As it can be seen from the results in Tables 4-7, the methods that estimated all variables very poorly is KM and the next poorest method is TPS. The remaining three methods (NN, IDWA, and MIDWA) are relatively performed best and these methods could be suggested to be applied for estimation of missing variables whenever necessary. When intercomparison was made method among the four variables (rainfall,
Table 5. Evaluation results for long-term average annual rainfall using ME, MAE, RMSE, and MRE.
Table 6. Evaluation results for long-term average wind speed using ME, MAE, RMSE, and MRE.
Table 7. Evaluation results for long-term mean temperature using ME, MAE, RMSE, and MRE.
wind speed, mean temperature and sunshine fraction), it is very difficult to predict wind speed using all methods as the errors are large relative to the remaining three variables. Therefore, it is not recommended to estimate missing values of wind speed using these evaluated methods, particularly for Diredawa station except NN method. The highest error recorded for KM is during estimation of rainfall, which shows that KM is not good method to be used for prediction of rainfall at some stations located in lowland areas like Dire Dawa, Gore, and Negele except for Awash. But this method is found to be good at Addis Ababa-Bole, Debremarkos, Gondar, and Mekele stations. Relatively, Sunshine fraction and mean temperature were estimated in a good way using NN, IDWA, and MIDWA methods.
Generally, NN, IDWA, and MIDWA were best methods relative to the remaining methods (KM and TPS) for all stations, except at Dire Dawa for estimation of wind speed using IDWA and MIDWA for both radial distances (r = 100 km and 200 km) for all variables. The summary of analysis result is summarized in Tables 5-8.
4. Conclusion
In this study, five spatial interpolation techniques (NN, IDWA, MIDWA, KM and TPS) were evaluated and compared using statistical indictors (ME, MAE,
Table 8. Evaluation results for long-term mean sunshine fraction using ME, MAE, RMSE, and MRE.
MRE and RMSE) for estimation of four meteorological variables (rainfall, mean temperature, wind speed and sunshine fraction) over complex topography of Ethiopia by specifying radial distances of 100 km and 200 km. It was found that 100 km was not effective even though it is recommended in many kinds of literatures. Hence, 200 km was selected for further analysis. The result of the analysis showed that KM and TPS methods are not good methods and NN, IDWA, and MIDWA methods are the best methods relatively. Estimation of rainfall in lowland areas like Diredawa, Gore, and Negele using KM is not good unlike that of Awash which has shown better results. When intercomparison is made among methods for the four variables (rainfall, wind speed, mean temperature, and sunshine fraction), it is very difficult to predict wind speed using all methods as the errors are large relative to the remaining three variables. This is also true for KM in predicting rainfall. Therefore, it is not recommended to estimate missing values of wind speed using these evaluated methods, particularly for Dire Dawa station except NN method. Mean temperature and sunshine fraction were estimated in a good way using NN, IDWA, and MIDWA methods.
Acknowledgements
I would like to thank my wife Etabezahu Tadese Belachew for her encouraging words and care during the unforgettable time of my life. This is not only my work but yours as well. Next, I appreciate the constructive suggestions give by the reviewer Wong Rui (Ray) from Journal of Water Resource and Protection (JWARP) editorial office.
Finally, this research did not receive any grant from funding agencies in the public, commercial or not-for-profit sectors.
Cite this paper
Boke, A.S. (2017) Comparative Evaluation of Spatial Interpolation Methods for Estimation of Missing Meteorological Variables over Ethiopia. Journal of Water Resource and Protection, 9, 945-959. https://doi.org/10.4236/jwarp.2017.98063
References
- 1. Presti, R.Lo., Barca, E. and Passarella, G. (2010) A Methodology for Treating Missing Data Applied to Daily Rainfall Data in the Candelaro River Basin (Italy). Environmental Monitoring and Assessment, 160, 1-22.
https://doi.org/10.1007/s10661-008-0653-3 - 2. Xia, Y., Fabian, P., Stohl, A. and Winterhalter, M. (1999) Forest Climatology: Estimation of Missing Values for Bavarian, Germany. Agricultural and Forest Meteorology, 96, 131-144.
- 3. Caldera, H.P.G.M., Piyathisse, V.R.P.C. and Nandalal, K.D.W. (2016) A Comparison of Methods of Estimating Missing Daily Rainfall Data. Engineer, XLIX, 1-8.
https://doi.org/10.4038/engineer.v49i4.7232 - 4. Burhanuddin, S.N.Z.A., Denis, S.M. and Ramli, N.M. (2015) Geometric Median for Missing Rainfall Data Imputation. AIP Conference Proceedings, 1643.
https://doi.org/10.1063/1.4907433 - 5. Villazón, M.F. and Willems, P. (2010) Filling Gaps and Daily Disaccumulation of Precipitation Data for Rainfall-Runoff Model. BALWOIS 2010, Ohrid, 25-29 May 2010.
- 6. Wong, K.J., Fung, K.W. and Che, C. (2012) A Comparative Analysis of Soft Computing Techniques Used to Estimate Missing Precipitation Records. 2012 19th ITS Biennial Conference, Bangkok, 18-21 November 2012.
- 7. Ramos-Calzado, P., Gomez-Camacho, J., Perez-Bernal, F. and Pita-Lopez, M.F. (2008) A Novel Approach to Precipitation Series Completion in Climatological Datasets: Application to Andalusia. International Journal of Climatology, 28, 1525-1534.
https://doi.org/10.1002/joc.1657 - 8. Li, J. and Heap, A.D. (2008) A Review of Spatial Interpolation Methods for Environmental Scientists. Geosciences Australia, Record 2008/23, 137 p.
- 9. Hijmans, R.J., Cameron, S.E., Parra, J.L. and Jones, P.G. (2005) Very High Resolution Interpolated Climate Surfaces for Global Land Areas. International Journal of Climatology, 25, 1965-1978.
https://doi.org/10.1002/joc.1276 - 10. Jarvis, C.H. and Stuart, N. (2001) A Comparison among Strategies for Interpolating Maximum and Minimum Daily Air Temperatures. Part II: The Interaction between Numbers of Guiding Variables and the Type of Interpolation Method. Journal of Applied Meteorology, 40, 1075-1084.
https://doi.org/10.1175/1520-0450(2001)040<1075:ACASFI>2.0.CO;2 - 11. Mardikis, M.G., Kalivas, D.P. and Kollias, V.J. (2005) Comparison of Interpolation Methods for Prediction of Reference Evapotranspiration—An Application in Greece. Water Resources Management, 19, 251-278.
https://doi.org/10.1007/s11269-005-3179-2 - 12. Coulibaly, M. and Becker, S. (2007) Spatial Interpolation of Annual Precipitation in South Africa-Comparison and Evaluation of Methods. Journal of Water International, 32, 494-502.
https://doi.org/10.1080/02508060708692227 - 13. Eklundh, L. and Pilesjo, P. (1990) Regionalization and Spatial Estimation of Ethiopian Mean Annual Rainfall. International Journal of Climatology, 10, 473-494.
https://doi.org/10.1002/joc.3370100505 - 14. Derib, S.D. and Diekkruger, B. (2011) Comparison of Spatial Interpolation Methods for Filling Daily Rainfall Missing Data, Blue Nile Basin, Ethiopia. Development on Margin, Bonn, 5-7 October 2011.
- 15. Grieser, J., Gommes, R. and Bernardi, M. (2006) New Local Climate Estimator of FAO. Geophysical Research Abstracts, 8, Article ID: 08305.
- 16. Awulachew, S.B., Yilma, A.D., Loulseged, M., Loiskandl, W., Ayana, M. and Alamirew, T. (2007) Water Resources and Irrigation Development in Ethiopia. International Water Management Institute, Colombo.
- 17. Worldometeres (2016) Ethiopia Population.
http://www.worldometers.info/worldpopulation/ethiopia-population/ - 18. Seleshi, Y. and Zanke, U. (2004) Recent Changes in Rainfall and Rainy Days in Ethiopia. International Journal of Climatology, 24, 973-983.
https://doi.org/10.1002/joc.1052 - 19. Golkhatmi, N.S., Sanaeinejad, S.H., Ghahraman, B. and Pazhand, H.R. (2012) Extended Modified Inverse Distance Method for Interpolation-Rainfall. International Journal of Engineering Inventions, 1, 57-65.
- 20. Hutchinson, M.F. (1995) Interpolating Mean Rainfall Using Thin Plate Smoothing Splines. International Journal of Geographic Information Systems, 9, 385-403.
https://doi.org/10.1080/02693799508902045 - 21. Apaydin, H., Sonmez, F.K. and Yildirim, Y.E. (2004) Spatial Interpolation Techniques for Climate Data in the GAP Region in Turkey. Climate Research, 28, 31-40.
https://doi.org/10.3354/cr028031 - 22. Hutchinson, M.F., Mckenney, D.W., Lawrence, K., Pedlar, J.H., Hopkinson, R.F., Milewsha, E. and Papadopol, P. (2009) Development and Testing of Canada-Wide Interpolated Spatial Models of Daily Minimum-Maximum Temperature and Precipitation for 1961-2003. Journal of Applied Meteorology and Climatology, 48, 725-741.
https://doi.org/10.1175/2008JAMC1979.1 - 23. Gomez, M.R.S. (2007) Spatial and Temporal Rainfall Gauge Data Analysis and Validation with TRMM Microwave Radiometer Surface Rainfall Retrievals. Master’s Thesis, International Institute for Geo-Information Science and Earth Observation, Enschede.
- 24. Wong, D.W., Yuan, L. and Perlin, S.A. (2004) Comparison of Spatial Interpolation Methods for the Estimation of Air Quality Data. Journal f Exposure Analysis and Environmental Epidemiology, 14, 404-415.
https://doi.org/10.1038/sj.jea.7500338 - 25. Stahl, K., Moore, R.D., Floyer, J.A., Asplin, M.G. and McKendry, I.G. (2006) Comparison of Approaches for Spatial Interpolation of Daily Air Temperature in a Large Region with Complex Topography and Highly Variable Station Density. Agricultural and Forest Meteorology, 139, 224-236.
https://doi.org/10.1016/j.agrformet.2006.07.004 - 26. Thornton, P.E., Running, S.W. and White, M.A. (1997) Generating Surfaces of Daily Meteorological Variables over Large Regions of Complex Terrain. Journal of hydrology, 190, 214-251.
https://doi.org/10.1016/S0022-1694(96)03128-9



