Journal of Water Resource and Protection
Vol.09 No.01(2017), Article ID:73594,18 pages
10.4236/jwarp.2017.91006
Parameter Uncertainty Estimation by Using the Concept of Ideal Data in GLUE Approach
Junjun Zhu, Hong Du
College of Resources and Environment, South-Central University for Nationalities, Wuhan, China

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 8, 2016; Accepted: January 16, 2017; Published: January 19, 2017
ABSTRACT
The hydrological uncertainty about NASH model parameters is investigated and addressed in the paper through “ideal data” concept by using the Generalized Likelihood Uncertainty Estimation (GLUE) methodology in an application to the small Yanduhe research catchment in Yangtze River, China. And a suitable likelihood measure is assured here to reduce the uncertainty coming from the parameters relationship. “Ideal data” is assumed to be no error for the input-output data and model structure. The relationship between parameters k and n of NASH model is clearly quantitatively demonstrated based on the real data and it shows the existence of uncertainty factors different from the parameter one. Ideal data research results show that the accuracy of data and model structure are the two important preconditions for parameter estimation. And with suitable likelihood measure, the parameter uncertainty could be decreased or even disappeared. Moreover it is shown how distributions of predicted discharge errors are non-Gaussian and vary in shape with time and discharge under the single existence of parameter uncertainty or under the existence of all uncertainties.
Keywords:
Ideal Data, GLUE Methodology, Likelihood Measure, NASH Model, Yanduhe Catchment, Uncertainty Principles

1. Introduction
It is well known that the hydrological processes are very complicated and influenced by climate, weather, geographic and geomorphic conditions, underlying surface conditions and that it is very difficult to obtain the hydrographic features (precipitation, evaporation, discharge etc.) as well as the spatial and temporal distributions of hydrologic cycle features precisely. For all of these reasons, the accuracy of hydrological modeling will be influenced by these uncertainties.
The randomness and fuzziness of the hydrological phenomenon are the primary causes for the modeling uncertainty. Hydrologists [1] [2] [3] [4] [5] have discussed such uncertainties originated by such causes as input-output data, hydrological model structure and model parameter. In particular, the uncertainty of the hydrological data can be summarized as below: 1) Representativeness of the distribution character and mathematical expectation of hydrological features. Taking the rainfall as an example, as heterogeneityand variability of the precipitation spatial distribution, maybe the information obtained in fixed rainfall station network is inaccurate to be used as mean value in an area; 2) measurement error. As the existence of the instrument error or fault and observer’s operation or evaluation error for the flood monitoring system, there must be input-output error for modeling; 3) lack reliable information for some hydrologic features.
Analogously, the model uncertainty can be summarized as below: 1) Since the knowledge limitations of hydrological processes, the descriptions of such pro- cesses may be approximate or unreasonable; 2) most mathematical and physical functions used in complex processes calculation are simplified; 3) many models cannot reflect the influence of environmental factors, such as global climate and land cover change due to human activities, to the run off process; 4) effective computing methods are needed. The rainfall-runoff is a continuous process that is simulated by the model in a discrete way causing inevitable errors. Besides, different discrete ways could have different influences; 5) model parameter values are difficult to be obtained by either measurement or prior estimation.
The research of parameter uncertainty is fundamental and meaningful. Once the hydrological model is confirmed, the parameters will be the key point for the modeling validity: the modeling will stand or fall according to the parameters. Premier researches about modeling uncertainty are mainly about model parameters but with the existence of other uncertainties, such as the Generalized Likelihood Uncertainty Estimation (GLUE) methodology [4] [6] , the Shuffled Complex Evolution Metropolis algorithm (SCEM-UA) [7] , and the Markov Chain Monte Carlo (MCMC) method [8] . All these methods were aimed to represent the parameter uncertainty but ignored the influence of other uncertainty factors. Therefore, the key point now is how to avoid or decrease the influences of input-output data uncertainty and model structure uncertainty for the exact estimation of the parameters. For this, “ideal data” is proposed in the paper to do the parameter uncertainty and interaction estimation by using GLUE methodology. And meanwhile the likelihood measure is also studied here. The proposed approach is applied to the well-known NASH runoff model considering as case study in Yanduhe basin of Yangtze River, China.
2. Theoretical Background
For the sake of completeness, the main theoretical background of involved models and methods are briefly described in what follows.
2.1. The GLUE Methodology
The GLUE procedure recognizes the equivalence of different sets of parameters in the calibration of models. It is based upon running a model with different sets of parameter values chosen randomly from the specified spatial distributions. Many papers have applied this methodology and emphasize the effects of the likelihood measure in the whole applying process [9] [10] . The term “likelihood” was used in a general sense, as a fuzzy, belief, or possible measure of how well the model conforms to the observed behavior of the system [4] , yet not in the restricted sense of maximum likelihood theory which is developed under specific assumptions of zero mean, normally distributed errors [11] [12] . Moreover, it is subjective to choose a suitable threshold for the likelihood measure to identify the behavior of the model. In the past studies, usually the threshold was chosen subjectively on the scale of some summary goodness of fit index [13] [14] [15] . And the GLUE method is used well in uncertainty research [16] [17] .
Here in the application of GLUE methodology, for each set of parameters, whether the model is behavioral or not is determined by the likelihood value on a basis of comparing predicted and observed responses.
The requirements of the GLUE procedure are given as follows:
1) A formal definition of a likelihood measure. At this stage it is worth noting that a formal definition is required but the choice of a likelihood measure will be inherently subjective.
2) An appropriate definition of the initial range and the distributions of the parameters to be considered for a particular model.
3) Definition of a feasible threshold value.
2.2. NASH Model
The NASH model [18] [19] [20] [21] is a conceptual hydrological concentration model developed by Nash, J.E., and it is widely used in the watershed concentration simulation [22] [23] . In the model, the research basin is divided into a series of identical reservoirs, and the reallocation of the net rainfall in the catchment is assimilated to be an adjustment of the reservoirs. So the instantaneous unit hydrograph (IUH) can be deduced as Eq. (1):
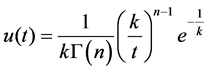 (1)
(1)
where 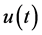 is the y-coordinate of instantaneous unit hydrograph;
is the y-coordinate of instantaneous unit hydrograph;  is the Gamma function;
is the Gamma function; 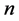 reflects the regulation and storage capacity of the basin, and it could be the number of the reservoirs, termed shape parameter;
reflects the regulation and storage capacity of the basin, and it could be the number of the reservoirs, termed shape parameter; 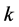 is the storage-discharge parameter of the reservoirs, termed scale parameter. The Nash model with its clear conception and simple structure has been used extensively in flood forecasting [24] [25] .
is the storage-discharge parameter of the reservoirs, termed scale parameter. The Nash model with its clear conception and simple structure has been used extensively in flood forecasting [24] [25] .
According to Eq. (1), when the net rainfall 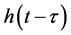 is given, the flow hydrograph at the basin outlet can be deduced as
is given, the flow hydrograph at the basin outlet can be deduced as
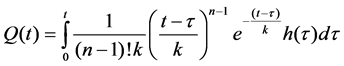 (2)
(2)
2.3. Generation of the Ideal Data
To avoid the input-output uncertainty and the model structure uncertainty, the concept of “ideal data” is proposed to do the research of model parameters uncertainty.
On the basis of the physical interpretation of the hydrological model and the characteristics of the research catchment, the model parameter spaces can be determined based on the prior information. Choose one set of parameters randomly in the parameter spaces as the “true parameter values”. First assume the input data has no error, then the input is called “ideal input”, and the “ideal output” can be calculated by using the “true parameter values” in the model.
For NASH model, the input is net rainfall and output is flow at the basin outlet.
3. Case Study and Results
The Yanduhe catchment in upper reaches of the Yangtze River basin covers a drainage area of 601 km2 where the annual average rainfall is about 1337 mm, and the runoff mainly comes from the rainfall. In this research catchment, four flood events are used in the case study (Table 1).
For NASH model, based on the physical interpretation and the catchment data, the spaces of the two parameters are k [0.5 - 4] and n [0.5 - 5]. The input is the net rainfall and the output is the surface runoff. Here the net rainfall is calculated by XAJ rainfall-runoff model [26] . In real data research, the error coming from XAJ model is assumed as input error of NASH model. In the application of GLUE methodology, it is done by Monte Carlo simulation, using uniform sampling in the specified parameter range.
In rainfall-runoff modeling we are often evaluating the errors in simulating a time series of discharge or other observed data. A classical statistical measure for evaluating goodness of fit based on the sum of squared errors or error variance is suggested by Nash and Sutcliffe (1970) in the form
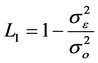 (3)
(3)
Table 1. The four flood events.
where 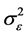 is the variance of the errors;
is the variance of the errors; 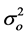 is the variance of the observations.
is the variance of the observations.
Another measure based on the sum of squared errors is the inverse error measure suggested by Box and Tiao (1992) in the form:
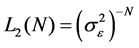 (4)
(4)
where 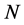 is a shaping parameter.
is a shaping parameter.
Here two likelihood measures were chosen for model and parameter uncertainty research by GLUE methodology.
3.1. GLUE Research under Real Data
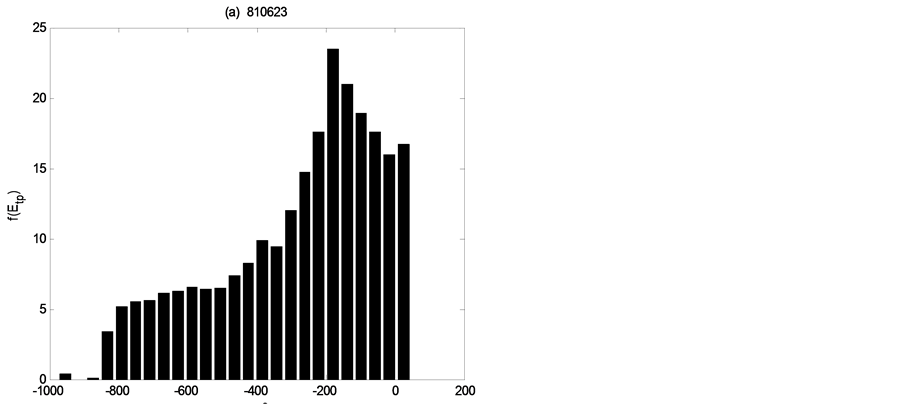
The GLUE methodology has been first applied to the real data (observed discharge) research with likelihood measure L1. In this study the choice of a model efficiency rejection criterion (<0) has been included, which assure all of the possible modeling results can be contained.
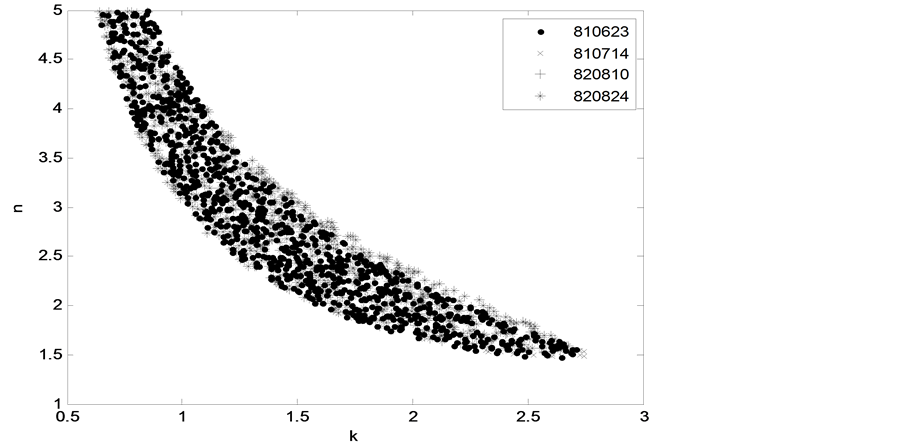
Scatter plots of parameters 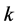 and
and 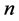 based on the likelihood measure L1are reported in Figure 1 and Figure 2 which show the effects of using different flood events with real input-output data. It can be seen that good and poor simulations are available virtually throughout the parameter ranges, and the effects of different flood events for parameters
based on the likelihood measure L1are reported in Figure 1 and Figure 2 which show the effects of using different flood events with real input-output data. It can be seen that good and poor simulations are available virtually throughout the parameter ranges, and the effects of different flood events for parameters  and
and 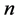 are seen clearly. It can be inferred that there is uncertainty of input-output data or others simultaneously to influence the distributions of the scatter plots.
are seen clearly. It can be inferred that there is uncertainty of input-output data or others simultaneously to influence the distributions of the scatter plots.
The results shown in Figure 1 and Figure 2 suggest that the parameter response surfaces are very complex and for different data that is for different events they vary showing the uncertainty of data.
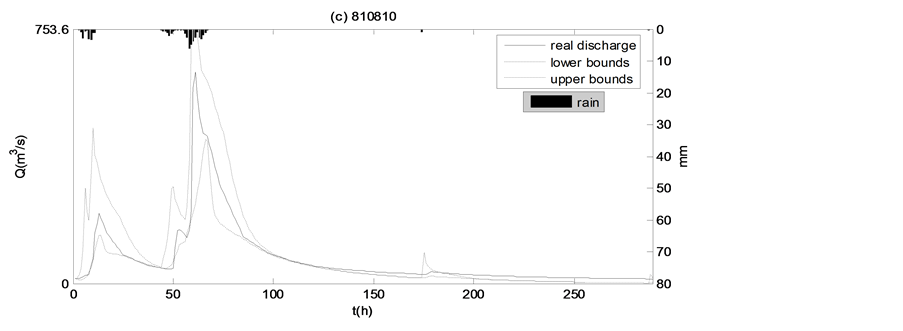
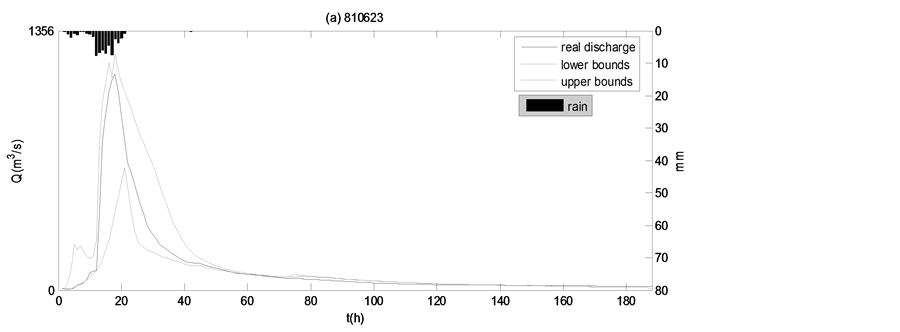
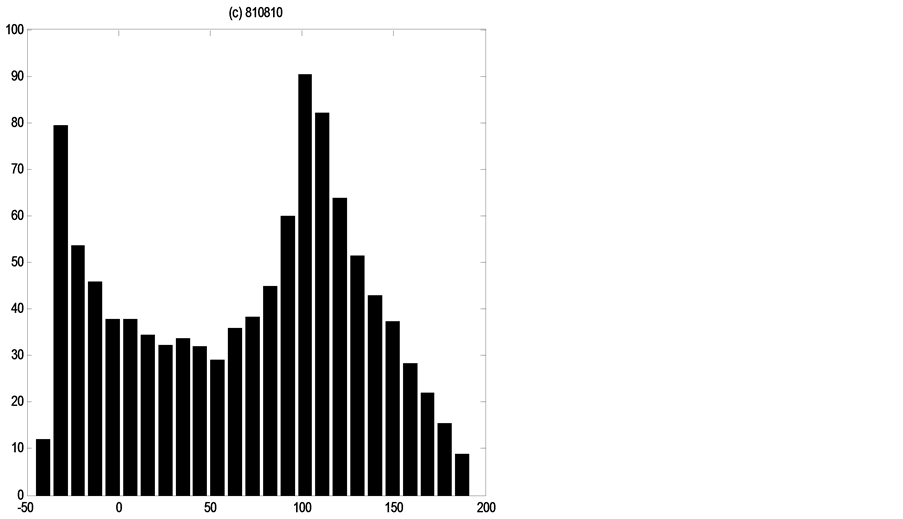
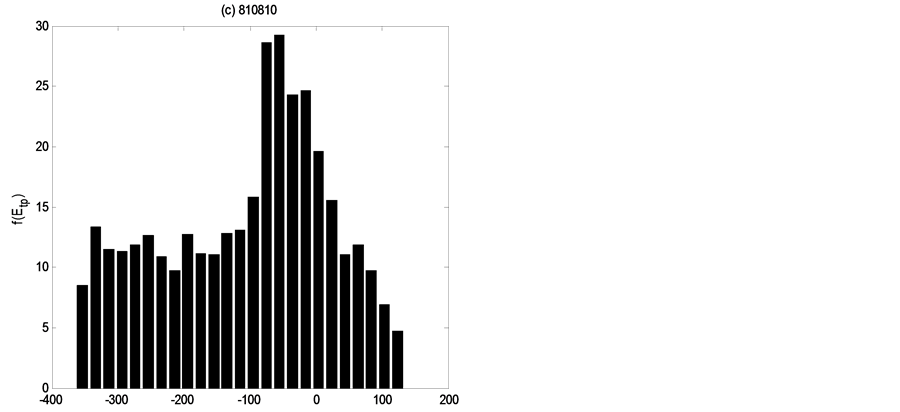
It is difficult in rainfall-runoff modeling to bracket all the discharge observations (or other predicted variables) within 90% of the calculated confidence bounds, as seen in Figure 3, the discharge is often outside of the 90% confidence bounds, which furthermore proves the data limitations as well as the model structure limitations.
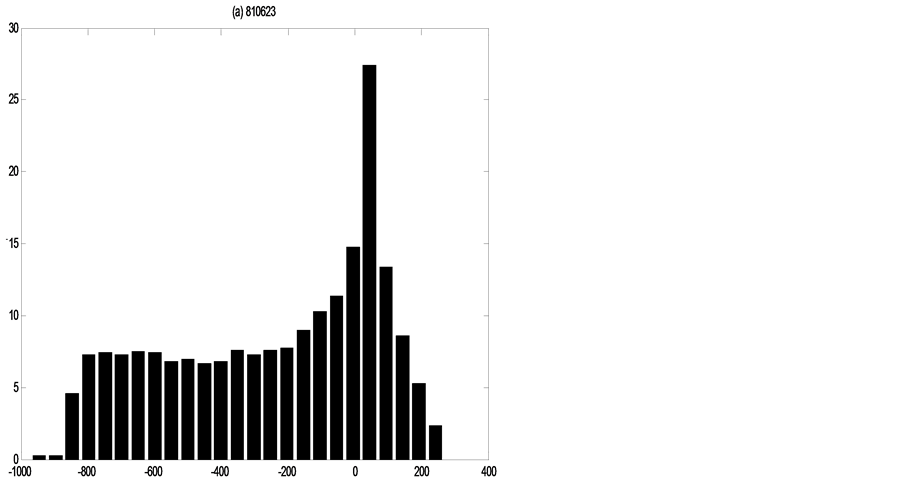
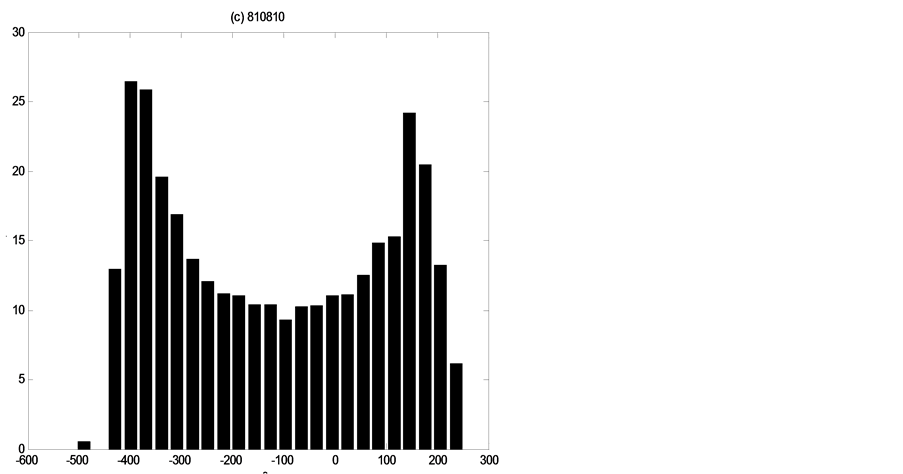
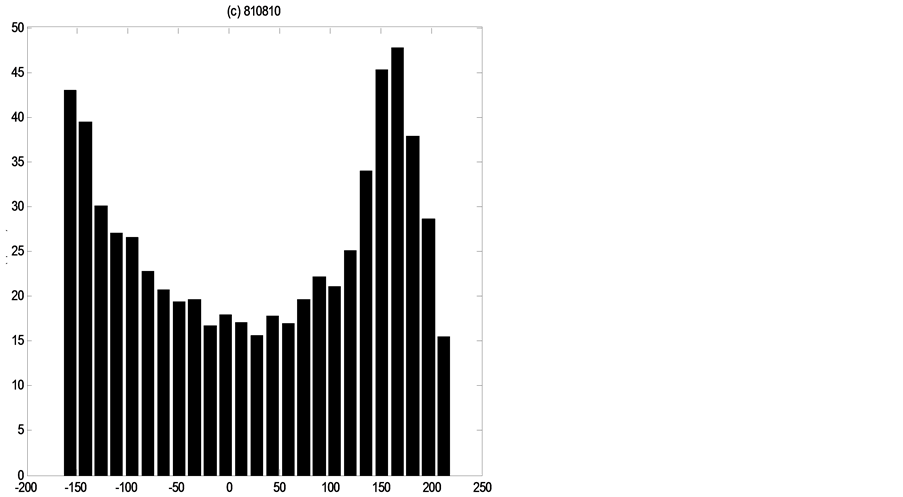
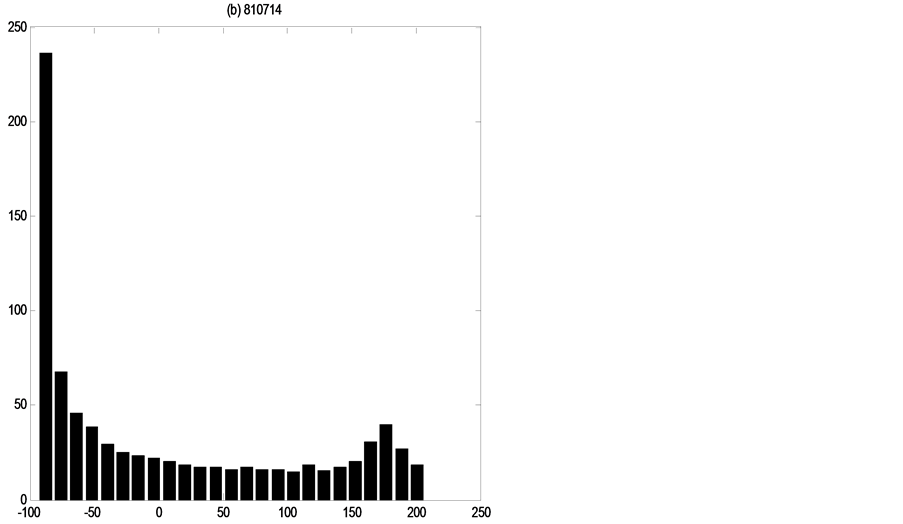
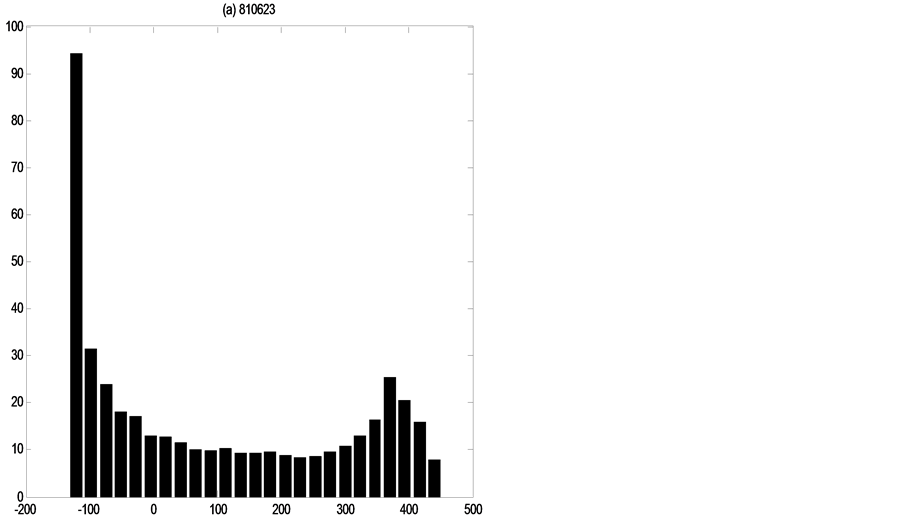
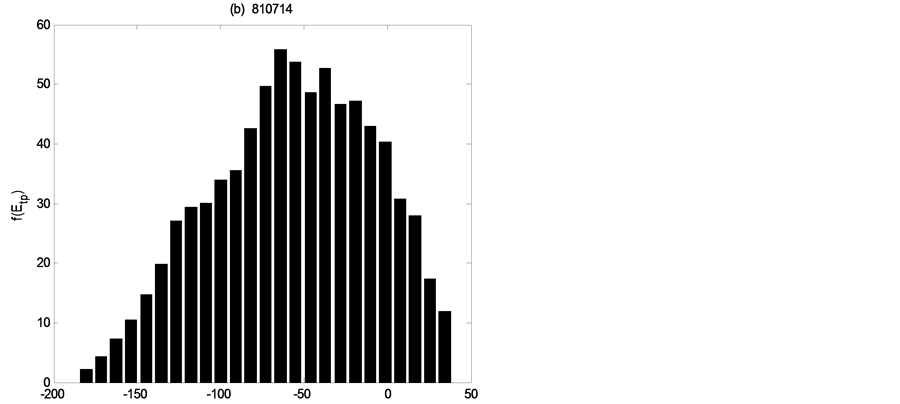
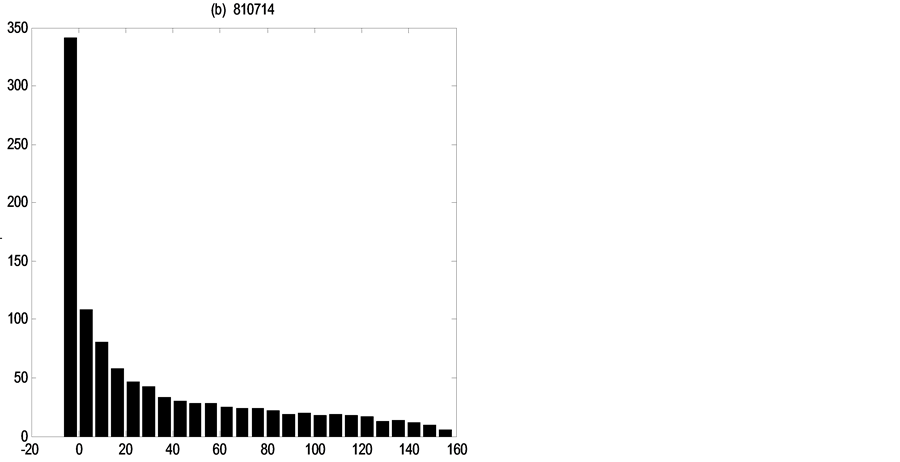
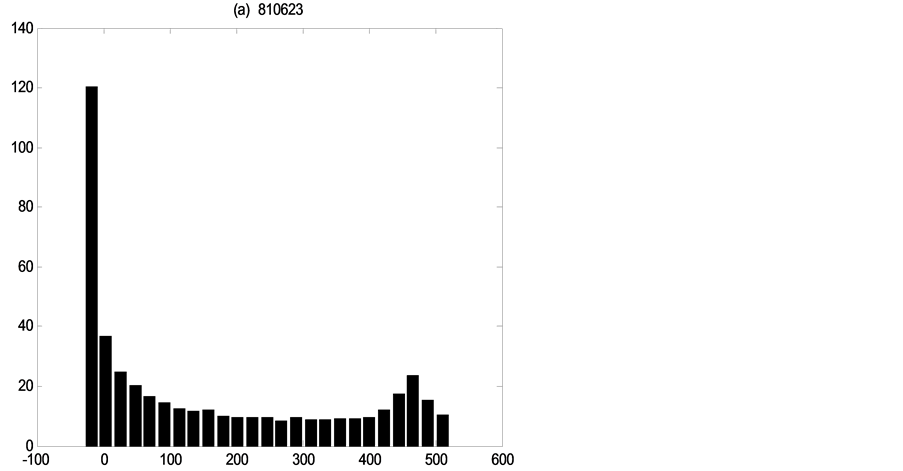
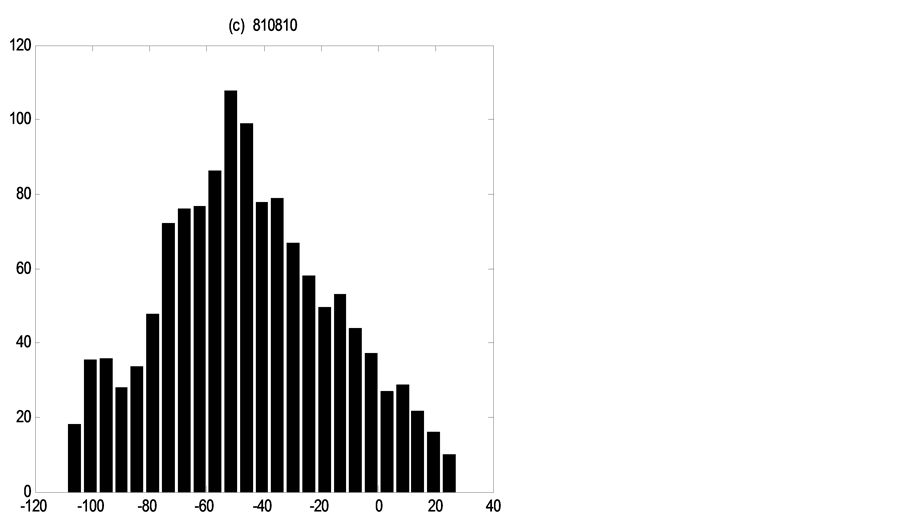
Figures 4-6 show the distribution of errors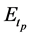 ,
, 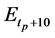
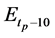
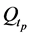
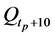
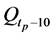
3.2. GLUE Research under Ideal Data
Then the GLUE methodology has been applied in parameter uncertainty research by proposing the “ideal data” to avoid the influence of other uncertainty factors. Following the above generation steps of the “ideal data”, one set of parameters is chosen as the “true parameter values”: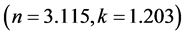
Figure 1. Scatter plots of efficiency results for parameter k in the four real flood events.
Figure 2. Scatter plots of efficiency results for parameter n in the four real flood events.
Figure 3. Ninety percent uncertainty bounds for simulations of the four real flood events in the Yanduhe catchment.
Figure 4. Error distributions at the point of 
model structure, under which situation the NASH parameter uncertainty is simulated by GLUE methodology. Here the choice of a high model efficiency rejection criterion (<0.90) has been included, since this is one way of trying to estimate the relationship of the two parameters.
Figure 7 and Figure 8 are scatter plots of efficiency results for parameters 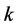

Comparing Figure 9 to Figure 3, it is easy to prove that all of the ideal discharges in NASH modeling are bracketed within the 90% calculated uncertainty
Figure 5. Error distributions at the point of 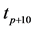
bounds, as shown in Figure 9. And for different flood events with ideal input data, the results are consistent, which demonstrate that there are no other uncertainty factors except the model parameters and assure the research accuracy of the model parameter uncertainty and correlation estimation. Obviously, the ideal data can assure the accuracy of the parameter uncertainty research.
Figure 10 shows the response surface of parameters 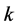

Figure 11 gives the scatter plots of parameters 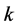
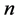
Figure 6. Error distributions at the point of 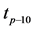
value greater than 0.98 trying to find the ridge line, from which we can assume that the distributions of the scatter plots can be matched by the function as below:
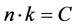
where 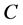
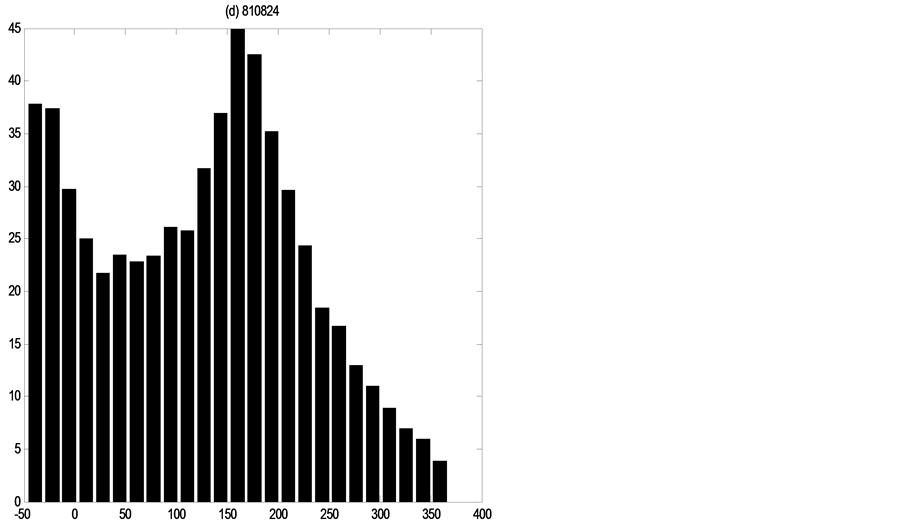
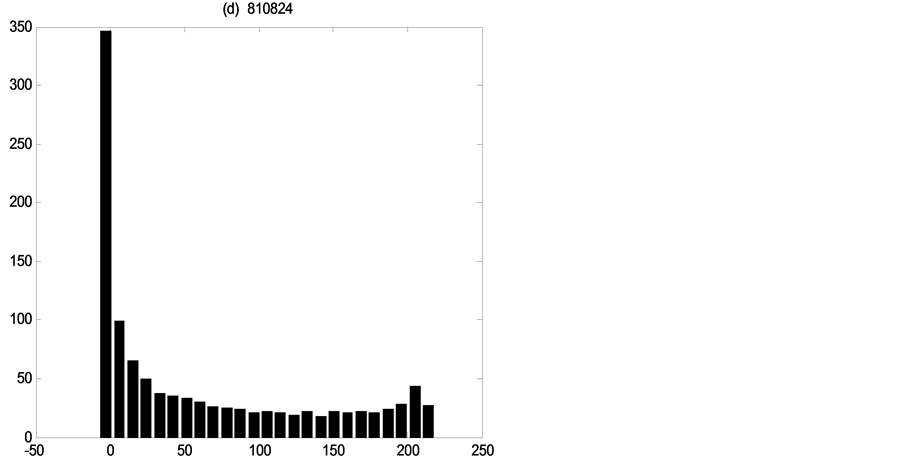
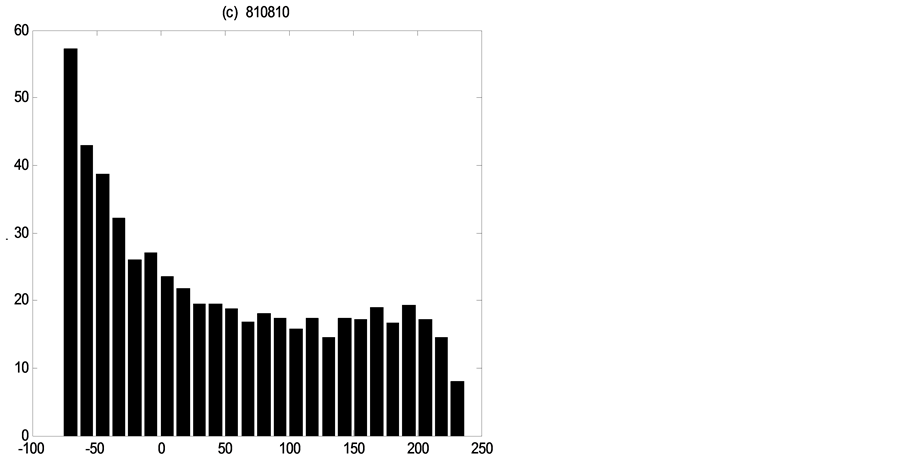
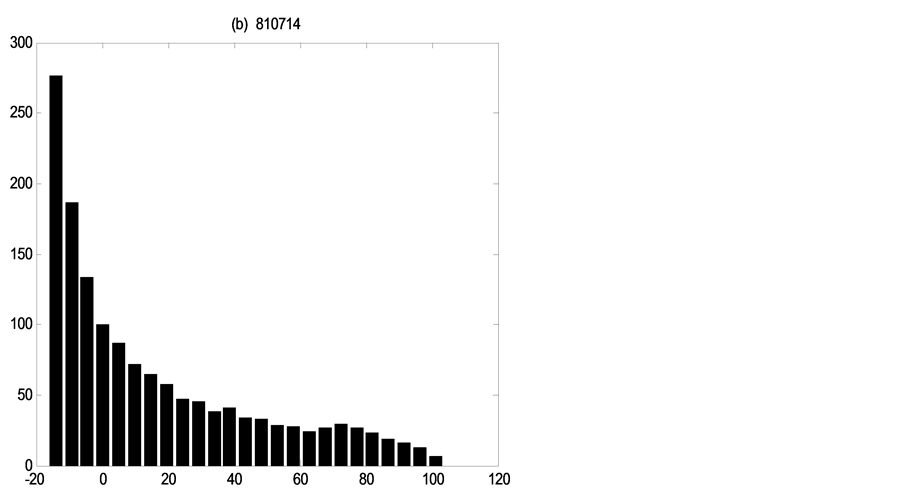
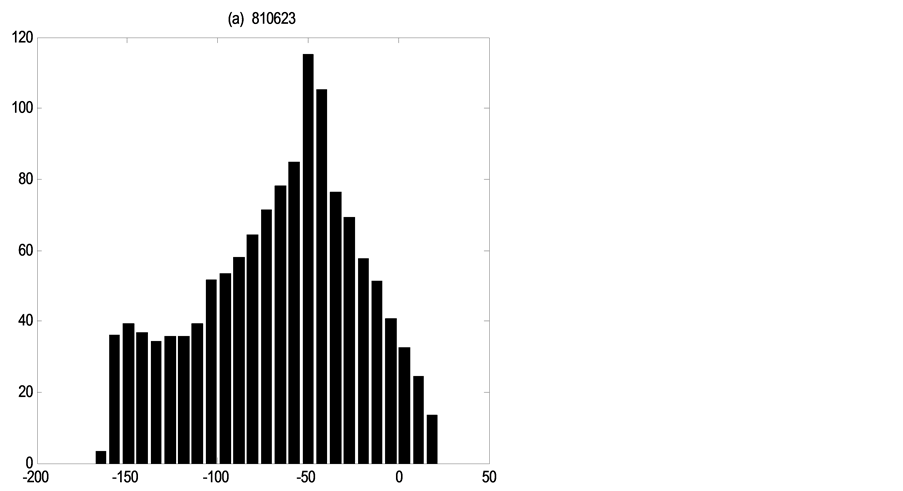
For the ideal data analysis, the uncertainty assessment refers only to the parameters, so it is accurate to analyze the error distributions of the discharges as the parameter errors. Same as the real data research, Figures 12-14 show for
Figure 7. Scatter plots of efficiency results for parameter k in the four ideal flood events.
Figure 8. Scatter plots of efficiency results for parameter n in the four ideal flood events.
Figure 9. Ninety percent uncertainty bounds for simulations of the four ideal flood events in the Yanduhe catchment.
Figure 10. Ideal data analysis: Response surface for parameter k and n with goodness of fit represented as contours.
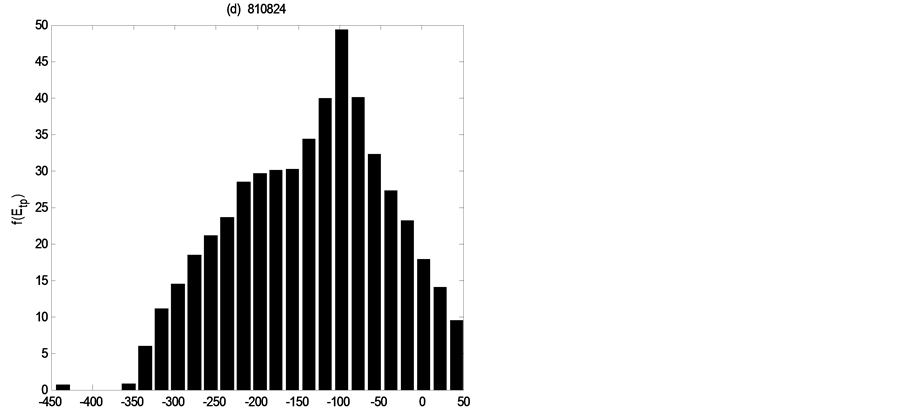
each flood event the error distributions of three discharge values, which demonstrate how distributions are non-Gaussian and vary in shape through time under the single existence of parameters uncertainty.
Figure 15 is the research result under idea data based on the likelihood L2 with parameter N = 20. For the four flood events, all of the “real parameters of model” are obtained in the figure.
Figure 11. Response surface for 
Figure 12. Error distributions at the point of 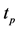
Figure 13. Error distributions at the point of 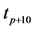
4. Conclusions
The paper proposes the concept of “ideal data” for parameter uncertainty assessment. The analysis is carried out for the NASH model parameters 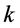
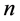
In idea data research, the consistent results from the different flood events demonstrate that there are no other uncertainty factors except the model para-meters, which assure the research accuracy of the model parameters uncertainty and correlation estimation. Obviously with the ideal data, the estimation for parameters uncertainty is accurate and reliable. And with suitable likelihood measure, the parameter uncertainty could be disappeared. The results also clearly show that under ideal data, the real parameter set is obtained, but the results also show that the distributions of errors are not Gaussian distribution as which are always assumed.
In real data research, when the model is confirmed the uncertainty due to both parameter uncertainty and data uncertainty. And the ideal data research show that the parameter uncertainty depends on the relationship between the two parameters. So the way to deal with the parameter uncertainty is how to reduce the correlation of the two parameters or confirm their correlation by constant function. But with likelihood L2 the uncertainty from the parameters correlation could be decreased in real data research
Figure 14. Error distributions at the point of 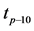
Figure 15. Response surface for parameters k and n under ideal data with likelihood L2.
The distributions of errors from model structure uncertainty, data uncertainty and model parameter uncertainty or from single model parameter uncertainty are non-Gaussian, and furthermore, changeable in each rainfall-runoff event. Meanwhile for different flood events they are also different. So it is not reasonable to assume the errors with this certain kind of distribution. Comparing these to the results from ideal data estimation, the mixed uncertainties make the error distributions more complicated.
Suitable likelihood measure is very important for uncertainty estimation and parameters determination. While the accurate data and perfect model structure are the two important factors for C. They are the preconditions for the estimation of model parameter uncertainty and interaction.
Acknowledgements
This study was financially supported by the Provincial Natural Science Foundation of Hubei (BZY14026) and the Fundamental Research Funds for the Central Universities, South-Central University for Nationalities (CZQ13006).
Cite this paper
Zhu, J.J. and Du, H. (2017) Parameter Uncertainty Estimation by Using the Concept of Ideal Data in GLUE Approach. Journal of Water Resource and Protection, 9, 65-82. http://dx.doi.org/10.4236/jwarp.2017.91006
References
- 1. Kuczera, G. (1983) Improved Parameter Inference in Catchment Models: Evaluating Parameter Uncertainty. Water Resources Research, 19, 1151-1162.
https://doi.org/10.1029/WR019i005p01151 - 2. Melching, C.S. (1995) Reliability estimation. In: Singh, V.P., Ed., Computer Models of Watershed Hydrology. Water Resources Publications, Highlands Ranch, CO, Chapter 3.
- 3. Zhao, R.J. (1989) Comparative Analysis Research of Hydrology Models. Journal of China Hydrology, No. 6, 1-5.
- 4. Beven, K.J. and Binley, A. (1992) The Future of Distributed Models: Model Calibration and Uncertainty Prediction. Hydrology Processes, 6, 279-298.
https://doi.org/10.1002/hyp.3360060305 - 5. Rui, X.F., Liu F.G. and Xin, Z.X. (2007) Advances in Hydrology and Some Frontier Problems. Advances in Science and Technology of Water Resources, 27, 75-79.
- 6. Page, T., Whyatt, J.D., Beven, K.J. and Metcalfe, S.E. (2004) Uncertainty in Modelled Estimates of Acid Deposition across Wales: A GLUE Approach. Atmospheric Environment, 38, 2079-2090.
https://doi.org/10.1016/j.atmosenv.2004.01.029 - 7. Vrugt, J.A., Gupta, H.V., Bouten, W. and Sorooshian, S. (2003) A Shuffled Complex Evolution Metropolis Algorithm for Optimization and Uncertainty Assessment of Hydrologic Model Parameters. Water Resources Research, 39, 1201.
https://doi.org/10.1029/2002WR001642 - 8. Kuczera, G. and Parent, E. (1998) Monte Carlo Assessment of Parameter Uncertainty in Conceptual Catchment Models: The Metropolis Algorithm. Journal of Hydrology, 211, 69-85.
https://doi.org/10.1016/S0022-1694(98)00198-X - 9. Beven, K.J. and Freer, J. (2001) Equifinality, Data Assilimilation, and Uncertainty Estimation in Mechanistic Modeling of Complex Environmental Systems Using the GLUE Methodology. Journal of Hydrology, 249, 11-29.
https://doi.org/10.1016/S0022-1694(01)00421-8 - 10. Blasone, R.S., Vrugt, J.A., Madsen, H., Rosbjerg, D., Robinson, B.A., Zyvoloski, G.A. (2008) Generalized Likelihood Uncertainty Estimation (GLUE) Using Adaptive Markov Chain Monte Carlo Sampling. Advances in Water Resources, 31, 630-648.
https://doi.org/10.1016/j.advwatres.2007.12.003 - 11. Sorooshian, S. (1981) Parameter Estimation of Rainfall-Runoff Models with Heteroscedastic Stream Errors: The Noninformative Data Case. Journal of Hydrology, 52, 127-138.
https://doi.org/10.1016/0022-1694(81)90099-8 - 12. Sorooshian, S. and Dracup, J.A. (1980) Stochastic Parameter Estimation Procedure for Hydrologic Rainfall-Runoff Models: Correlated and Heteroscedastic Error Cases. Water Resources Research, 16, 430-442.
https://doi.org/10.1029/WR016i002p00430 - 13. Freer, J., Beven, A.M. and Ambroise, B. (1996) Bayesian Estimation of Uncertainty in Runoff Prediction and the Value of Data: An Application of the GLUE Approach. Water Resources Research, 32, 2161-2173.
https://doi.org/10.1029/95WR03723 - 14. Candela, A., Noto, L.V. and Aronica, G. (2005) Influence of Surface Roughness in Hydrological Response of Semiarid Catchments. Journal of Hydrology, 313, 119-131.
https://doi.org/10.1016/j.jhydrol.2005.01.023 - 15. Choi, H.T. and Beven, K.J. (2007) Multi-Period and Multi-Criteria Model Conditioning to Reduce Prediction Uncertainty in an Application of TOPMODEL within the GLUE Framework. Journal of Hydrology, 332, 316-336.
https://doi.org/10.1016/j.jhydrol.2006.07.012 - 16. Wu, H.J. and Chen, B. (2015) Evaluating Uncertainty Estimates in Distributed Hydrological Modeling for the Wenjing River Watershed in China by GLUE, SUFI-2, and ParaSol Methods. Ecological Engineering, 76, 110-121.
https://doi.org/10.1016/j.ecoleng.2014.05.014 - 17. Xue, C., Chen, B. and Wu, H.J. (2013) Parameter Uncertainty Analysis of Surface Flow and Sediment Yield in the Huolin Basin in China. Journal of Hydrological Engineering, 19, 1224-1236.
https://doi.org/10.1061/(ASCE)HE.1943-5584.0000909 - 18. Nash, J.E. (1957) The Form of the Instantaneous Unit Hydrograph. Publications—International Association of Hydrological Sciences, 45, 114-121.
- 19. Nash, J.E. (1958) Determining Runoff from Rainfall. Proceedings of the Institution of Civil Engineers, 10, 163-184.
- 20. Nash, J.E. (1959) Systematic Determination of Unit Hydrograph Parameters. Journal of Geophysical Research, 64, 111-115.
https://doi.org/10.1029/JZ064i001p00111 - 21. Nash J.E. (1960) A Unit Hydrograph Study, with Particular Reference to British Catchments. Proceedings of the Institution of Civil Engineers, 17, 249-282.
https://doi.org/10.1680/iicep.1960.11649 - 22. Lee, Y.H. and Singh, V.P. (1998) Application of the Kalman Filter to the Nash Model. Hydrological Processes, 12, 755-767.
- 23. Kalinin, G.P. and Milyukov, P.I. (1958) On the Computation of Unsteady Flow in Open Channels. Meteorological Gidrologia, 10, 10-18.
- 24. Choi, Y., Lee, G. and Kim, J. (2011) Estimation of the Nash Model Parameters Based on the Concept of Geomorphologic Dispersion. Journal of Hydrological Engineering, 16, 806-817.
https://doi.org/10.1061/(ASCE)HE.1943-5584.0000371 - 25. Li, C., Guo, S. and Zhang, W. (2008) Use of Nash’s IUH and DEMs to Identify the Parameters of an Unequal-Reservoir Cascade IUH Model. Hydrological Processes, 22, 4073-4082.
https://doi.org/10.1002/hyp.7009 - 26. Zhao, R.J, Wang, P.L. and Hu, F.B. (1992) Relations between Parameter Values and Corresponding Natural Conditions of Xinanjiang Model. Journal of Hohai University, 20, 52-59.